一种固定远场法向位移的水泥环弹塑性应力解

张 磊, 刘海龙, 林 海, 董平华, 张羽臣

(中海石油(中国)有限公司天津分公司, 天津 300459)

0 引言

为了更精确地分析水泥环应力,针对目前水泥环应力解远场边界不固定的问题,应固定地层无限远场法向位移,并有必要把水泥环当作理想弹塑性材料,建立组合体应力和位移分布弹塑性模型。理论方面,国外学者利用解析或有限元方法对不同工况下套管-水泥环-地层组合体应力分布进行了大量的研究[1-7],国内学者利用弹性力学对套管载荷和水泥环力学完整性进行了大量分析[8-14]。国内学者[15-17]先后建立了套管-水泥环-地层系统的弹塑性解析解。范明涛和陈升[18-19]根据分步有限元的模拟思想,建立了考虑水泥环初始应力应变的井筒组合体数值模型,考虑了建井过程对井筒组合体的影响,在此基础上,求解了水泥环初始应力。工艺方面,刘阳和李治衡[20-21]对页岩气水平井和小间隙固井技术进行了研究。但大部分研究依然存在以下问题：求解物理模型未固定地层无限远处位移边界,不能消除建井过程对地层无限远处造成的应力及位移扰动影响,不完全符合实际。刘伟[22]提出了一种固定远场位移边界的套管-水泥环-地层组合体弹性解新模型,通过与有限元计算结果对比,符合度高。

该文通过借鉴文献[22]中基于固定地层远场法向位移边界的套管-水泥环-地层组合体应力分布求解思路,利用待定系数法建立了一种浅层固井水泥环受均匀地应力条件下理想弹塑性应力分布修正解,求解过程更方便,且消除了建井过程对远场位移和应力的扰动影响。此外,由于在一般情况下,套管强度远远高于水泥环和地层岩石,塑性区一般是由水泥环内壁向外壁逐渐发展,所以在讨论水泥环的完整性破坏时可以认为套管和地层始终处于弹性状态。在此基础上,分析了均匀地应力条件下水泥环的弹塑性受力与变形规律,以期对浅层水泥浆设计提供理论指导。

1 弹塑性模型的建立

水泥石作为一种特殊岩石,根据其力学变形破坏实验,应被当作一种弹塑性介质建立水泥环弹塑性应力解。基于弹塑性理论,为计算方便作如下假设：1)套管和地层为完全弹性体,水泥环为理想弹塑性介质；2)套管完全居中,固井质量良好；3)水平地应力为均匀地应力；4)研究对象变形属于平面应变问题。组合体理想弹塑性解力学模型如图1所示,套管内外壁半径分别是r1和r2,水泥环外径是r3,无限远地层半径可被看作r4。套管受内外压分别为pw和p2,水泥环受外压为p3,地层受外压为po,红色虚线是水泥环弹塑性边界,塑性区半径为rep,弹塑性边界处的层间压力为p。

图1 套管-水泥环-地层组合体理想弹塑性力学模型Fig.1 Ideal elastoplastic mechanical modelof casing-cement-stratum combination

1.1 套管和水泥环应力分布弹塑性解

根据厚壁圆筒弹性理论,套管和地层的径向、周向应力可以通过拉梅公式计算,结合弹性介质本构方程和几何方程,得到套管和水泥环在弹性区内的应力和位移分布,具体推导过程可参考文献[14-15],径向、周向应力和径向位移表达式如式(1)：

(1)

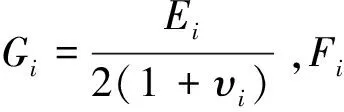
水泥环进入塑性以后,应满足平衡方程和屈服条件(见式(2))。由于水泥环材料性质和岩石比较接近,屈服条件选择摩尔库伦准则。设定应力应变符号以拉伸为负(下同)。

(2)

式中：c为水泥石的内聚力, MPa；φ为水泥石的内摩擦角,(°)。上标p表示塑性(下同)。

将式(2)中屈服条件与平衡方程联立,并结合边界条件(r=r2,σr=p2),可推导得到水泥环在塑性区的应力分布[17-18]。在塑性区,采用非关联流动,塑性体应变可以取为零,结合体积弹性定律[19]、几何方程及弹塑性区交界面处径向位移连续条件,可推导塑性区的位移分布[17-18],具体推导过程不再赘述。

(3)

(4)

1.2 地层应力分布弹塑性解

需要重点说明的是：文献[20]建立了一种套管-水泥环-地层组合体应力分布修正模型,与传统位移模型(见式(1))不同,该模型认为地层远场法向位移应该固定,建井过程对地层远场位移和应力不应造成扰动。所以,地层的弹性应力和位移分布表达式如式(5)所示,上标3代表地层岩石(下同)。从式(5)可以看出,r→∞时,地层远场位移为0。而式(1)中r→∞时,地层远场位移则不为0。

(5)

综上,对于套管-水泥环-地层组合体,不同介质交界面及水泥环弹塑性界面处的位移和应力连续,套管内壁处应力为套管内压力。所以应力边界及连续条件如式(6)：

(6)

式(6)中有F1,F2,L1,L2,A,p3和rep共7个待定系数,对应7个边界条件。求解7个方程可得均匀地应力条件下组合体理想弹塑性应力及位移分布。

当rep=r2时,水泥环第一界面处开始产生塑性变形破坏时对应的套压值,称为弹性极限内压；当rep=r3时,水泥环从第一界面到第二界面全部产生塑性变形,对应的临界套压值称为塑性极限内压,当套压小于弹性极限内压时,水泥只发生弹性变形,在工程当中是比较理想的。

2 水泥环力学完整性结果讨论

2.1 传统弹性解与弹塑性修正解对比

取参数r1,r2和re分别为113.00 mm,122.23 mm和155.58 mm；水平地应力po为16.5 MPa；套管弹性模量和泊松比分别为205 GPa和0.3；水泥环弹性模量和泊松比分别为4 GPa和0.25；地层弹性模量和泊松比分别为10 GPa和0.18；水泥环粘聚力和内摩擦角分别为7 MPa和30°。分别采用传统弹性、传统弹塑性和该文弹塑性解计算套管外壁径向接触应力随内压的变化,计算结果如图2所示。计算结果显示径向接触应力随套管内压的增大而增大。当套压大于弹性极限内压时,套管第二界面处所受载荷的弹塑性解大于弹性解,并且随套管内压增大,套管外壁载荷增加幅度变大,最大增幅为4.05%。其次,由于不固定远场位移,传统弹塑性解在套压为29.4 MPa时水泥环内壁开始进入塑性,而该文弹塑性解在31.2 MPa时水泥环内壁才开始进入塑性,且传统弹塑性解大于该文弹塑性解。总之,采用弹塑性理论进行固井水泥环强度设计更为安全,从上述弹塑性解析解可计算得出水泥环弹性极限内压,为固井设计防止水泥环产生塑性变形提供了理论依据。

2.2 水泥环力学完整性破坏分析

求解组合体沿井眼半径方向应力分布随套管内压变化规律,如图3所示。图3a为套管-水泥环-地层应力分布,图3b为水泥环区域应力分布放大结果。从图中计算结果可以看出：径向应力连续,周向应力不连续,无限远处接近于原场地应力。对于套管而言,由于套管内压较大,膨胀效应导致所受周向应力为拉应力。随套管内压增加,水泥环塑性区增加。套管内压由35 MPa增加到45 MPa时,塑性区由4.29 mm增加到18.96 mm。水泥环处径向应力始终为压应力,随套压增加而降低,受套管向外膨胀影响,周向应力有转变成拉应力趋势。所以,应防止套压过高导致水泥环产生塑性变形破坏。根据上述弹塑性解析解可计算得到水泥环弹性极限内压,为防止水泥环产生塑性变形提供了理论依据。

图3 组合体应力分布随套管内压变化规律Fig.3 Variation curve of combination stress distributionwith casing internal pressure

为了更好地计算水泥环应力,单独分析水泥环区域受力情况。固定套管内压为35 MPa,变化水泥环弹性模量为4 GPa和6 GPa,变化泊松比为0.20和0.25,求解沿井眼半径方向应力分布随水泥环力学参数变化规律,如图4所示。计算结果显示：随着弹性模量的降低,泊松比增加,水泥环塑性区半径降低。弹性模量由4 GPa增加到6 GPa时,塑性区由4.29 mm增加到19.54 mm。径向应力始终为压应力,但套管内压较高时,周向应力有变为拉伸应力的趋势。总之,随水泥环刚度降低,泊松比增加,水泥环塑性半径减小,可以避免内压降低时产生微环隙,有利于井筒完整性的维护。

图4 水泥环区域应力分布随水泥环力学参数变化规律Fig.4 Variation curve of stress distribution in the cement ring area with mechanical parameters of cement

3 实例计算

图5为水泥环塑性区的外径扩展曲线,当rep=r2时,计算得到水泥环弹性极限内压为35.6 MPa,当rep=r3时计算得到水泥环塑性极限内压为53.8 MPa,如果套压大于水泥环塑性极限内压,水泥环完全进入塑性。现场应控制最高套管内压不超过35.6 MPa,避免水泥环第一界面产生塑性变形,在套管内压卸载后可能造成第一界面分离,形成水泥“微环空”,在极端情况下可能会造成井底压力上窜,造成环空带压问题。现场套管试压时,井内钻井液密度为1.06 g/cm3,套管最大内压为30.4 MPa,小于水泥环弹性极限内压。现场测定固井质量合格(如图6所示),与计算分析结果比较符合。

图5 水泥环塑性区外径扩展曲线Fig.5 The outer diameter expansion curve of cement ring plastic zone

图6 水泥环SBT测井固井质量(SBT：分区水泥胶结测井)Fig.6 Cementing quality of cement ring SBT logging

4 结论

1)在固定地层无限远处法向位移基础上,利用待定系数法建立了受内外压力且具有Mohr-Coulomb屈服条件的厚壁筒弹塑性应力和位移修正解,消除了建井过程对地层远场位移和应力的扰动。该模型可以作为浅层或盐岩、膏岩等地应力均匀的地层和差应力较小的地层组合体力学完整性分析。

2)与传统弹性模型进行对比,当套管内压超过弹性极限内压时,套管外壁载荷的弹塑性解大于弹性解,且随着套管内压增大套管外壁载荷增加幅度变大。

3)随着套管内压增加,水泥环弹性模量增加,泊松比降低,水泥环塑性区增加,由4.29 mm增加到最大19.54 mm。径向应力始终为压应力,但套管内压较高时,周向应力有转变为拉伸应力的风险。