基于神经网络的MIMU动态误差标定与补偿方法

马一鸣， 陈 帅， 王国栋， 张 琨， 程 玉

(1.南京理工大学，南京 210000； 2.北京航天控制仪器研究所，北京 100000)

0 引言

惯性导航是一种独立性强、短时精度高、环境适应能力强的导航方法，通常与卫星导航结合构成组合导航系统，主要用于保证卫星拒止情况下的导航精度[1]。随着微机电技术的发展，微惯性测量单元(Miniature Inertial Measurement Unit，MIMU)因其低成本、小体积、低功耗、高可靠性、较强抗冲击性的特点在穿戴设备、智能汽车、小型无人机以及智能弹药等领域快速占据了市场[2]。由于MIMU自身存在系统性误差与随机误差，并且系统性误差占总误差的90%以上，因此研究如何补偿系统性误差以提高MIMU实际使用精度极其重要[3]。

由于计算位置、姿态与速度时需要对MIMU输出进行积分，因此，系统性误差对惯性导航系统的整体性能影响显著。通过MIMU的标定对其系统性误差进行补偿是使用MIMU必不可少的步骤。传统的标定方法是使用转台设备提供的角速度以及不同位置的重力加速度作为基准，利用测量数据与基准进行线性拟合，建立标定模型以达到补偿确定性误差的目的。然而，MIMU大多数时候在低转速区间工作，低转速区间陀螺仪输出具有强非线性，传统方法的补偿效果差[4]。当MIMU三轴同时存在角运动时，三轴加速度计与三轴陀螺仪不可避免存在耦合误差，传统的标定方法难以学习惯性器件复杂的误差特征，无法对误差进行有效、精确的补偿[5]。针对陀螺输出非线性问题，程章等[4]提出了使用BP神经网络对MEMS陀螺的输出进行补偿，设计了基于优先数的速率实验，但该方法忽略了加速度对陀螺的影响；文献[5-6]分别使用BP和径向基神经网络(RBFNN)补偿三轴加速度和角速度，但实验没有考虑到位置动态变化的连续性以及三轴角运动；李荣冰等[7]采用长短时记忆(LSTM)深度神经网络设计了MIMU标定方法,考虑了惯性数据的时序性以及多维要素影响，提高了误差模型精度；文献[8-9]利用BP神经网络方法对陀螺仪的温度漂移进行补偿，提高了陀螺仪的温度适应性。

神经网络具有极强的非线性映射能力以及泛化能力[10]。本文分别采用两种深度循环神经网络和两种浅层神经网络建立动态误差标定模型。设计转台内、中、外3轴角运动实验方法，对三轴加速度计与陀螺仪施加连续动态激励以及温度激励。最后，通过实验对比不同模型下的补偿效果，结果表明，门控循环单元(GRU)深度循环神经网络考虑了MIMU数据的时序性,从而达到了更好的误差补偿效果，并且相对于LSTM需要训练更少的参数。

1 理论模型

1.1 传统标定误差模型

考虑到陀螺仪与加速度计的零偏误差、标度因数误差、安装误差以及随机误差，建立如下误差模型

(1)

(2)

1.2 广义回归神经网络模型

广义回归神经网络(GRNN)是一种基于样本的神经网络模型，样本数据直接用于神经网络的计算，模型训练的负担小。通过样本在特征空间的映射，在训练数据较少的情况下也具有很好的学习能力与拟合能力。GRNN结构如图1所示，其中包含输入层、模式层、求和层以及输出层[11]。

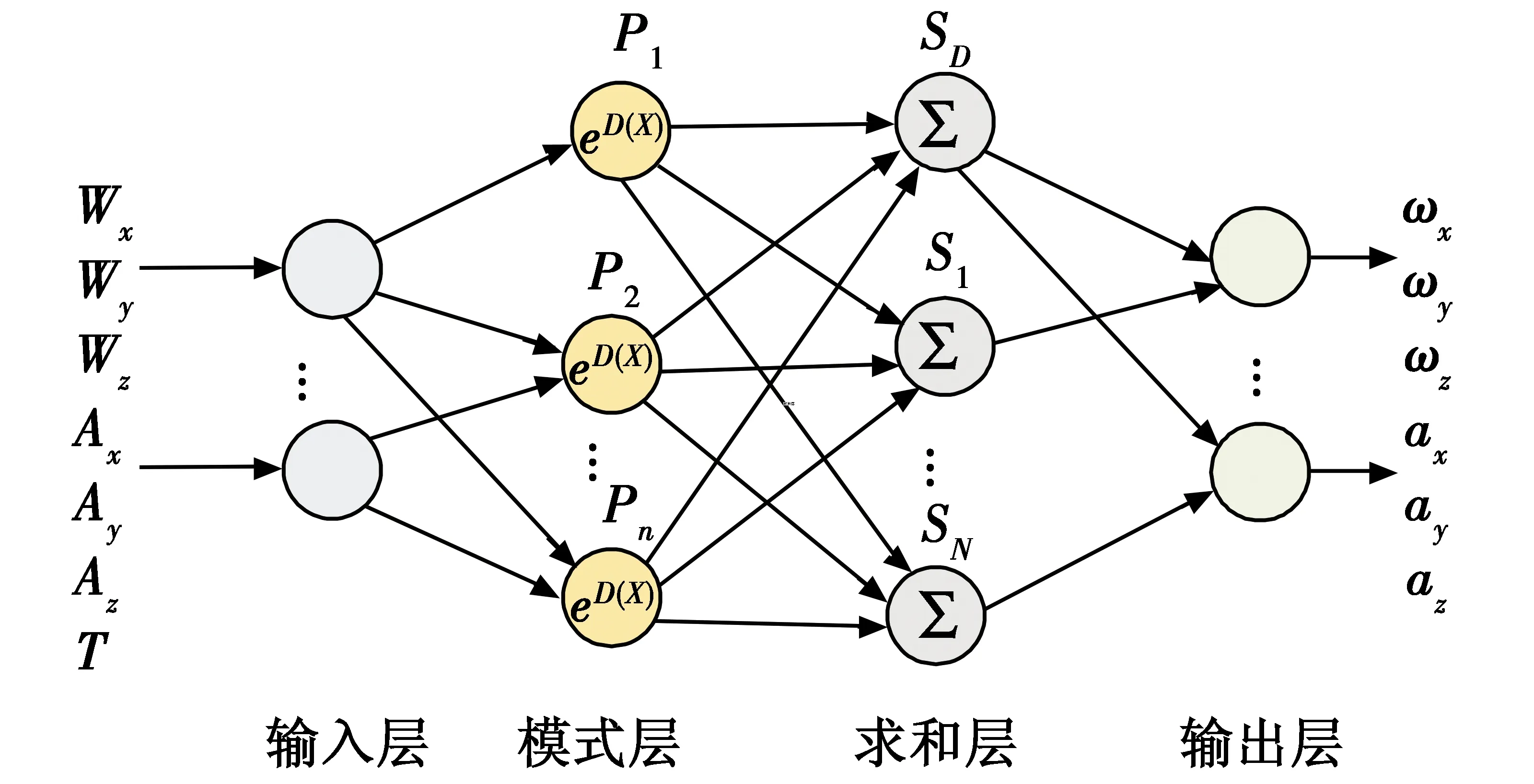
图1 GRNN结构图Fig.1 Structure diagram of GRNN

模式层神经元表达式为

(3)

式中:X代表输入向量;Xi代表样本的输入向量;n是样本数目;σ是平滑因子，控制着样本空间距离缩放程度，当σ趋于零时，Pi趋于零，输出只依赖于完全相同的样本，当σ趋于无穷时，Pi趋于1，输出依赖于所有样本的平均，所以需要适当地选取σ以达到考虑相似样本的目的。

求和层神经元表达式为

(4)

(5)

其中:SD为对模式层进行权值为1的求和;Sj为对模式层的加权求和;yj i代表样本i输出向量的第j个元素;N代表输出向量的维度。

输出层神经元的表达式为

(6)

GRNN的本质是对输入与样本之间的空间距离进行计算，并根据空间距离进行加权变换，从而得到输出。其中，通过将输入特征映射到高维的模式层能够更好地捕捉多维输入与多维输出之间的映射关系。

1.3 GRU深度神经网络模型

循环神经网络(Recurrent Neural Network，RNN)是针对时序问题提出的深度神经网络，但是当训练的时间序列较长时，在误差反向传播中会出现梯度消失与梯度爆炸的问题。为了解决这个问题，1997年HOCHREITER等提出了LSTM[12]，之后，2014年CHO等提出了GRU[13]。相对于LSTM，GRU需要训练的参数较少，并且在非语言建模任务中可以达到优于LSTM的效果[14]。

GRU神经元结构示意图见图2，其中包含了重置门与更新门，重置门用于决定是否忽略上一时刻的隐含层状态，更新门用来决定隐含层状态的更新。门控结构控制着隐含层状态对之前信息的记忆与遗忘。GRU的前向传播表达式为

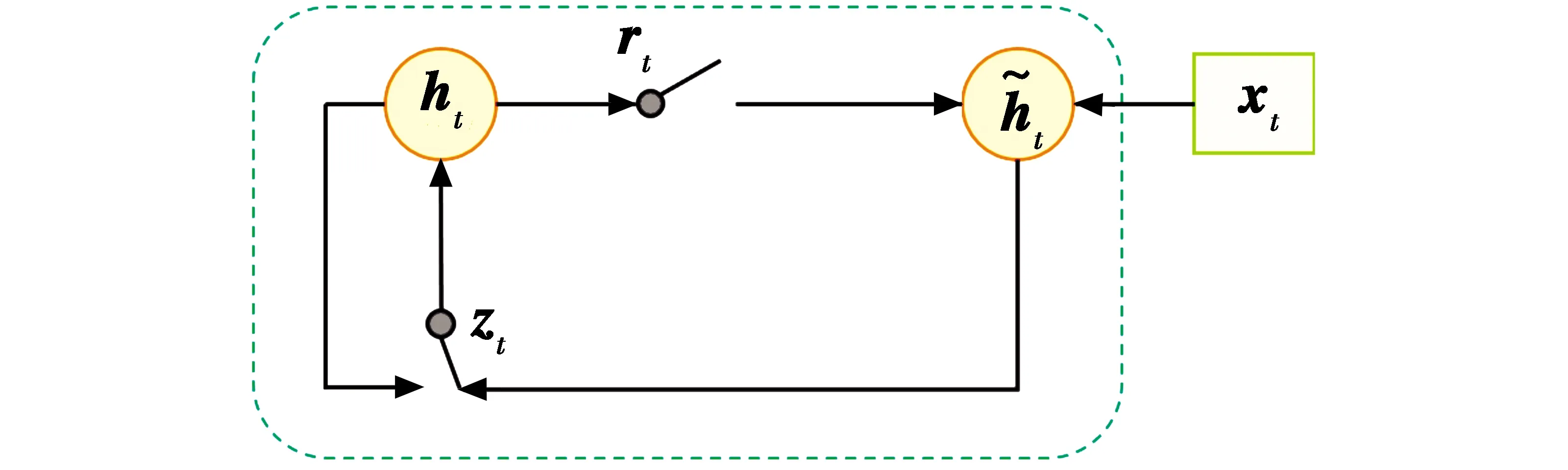
图2 GRU神经元结构示意图Fig.2 Schematic diagram of GRU neurons structure

rt=σ(Wrxt+Urht-1)

(7)

zt=σ(W′zxt+Uzht-1)

(8)

(9)

(10)

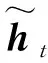
1.4 神经网络的输入输出结构设计

神经网络结构与参数需要根据学习的对象确定,尤其是输入层与输出层的选择。根据传统标定模型可知MIMU的测量输出与实际输出存在一定的映射关系。考虑到加速度计与陀螺仪输出之间的耦合误差和与温度有关的温度漂移误差，此处应存在MIMU测量输出、温度和MIMU实际输出之间的映射关系。因此，本文选择神经网络的输入为三轴陀螺仪测量的角速度Wx,Wy,Wz，三轴加速度计测量的加速度Ax,Ay,Az及温度T。神经网络的输出为三轴实际的角速度ωx,ωy,ωz和三轴实际的加速度ax,ay,az。其中，三轴实际角速度由转台的角速度转换得到，三轴实际的加速度由转台的角位置转换得到。神经网络整体工作结构如图3所示。

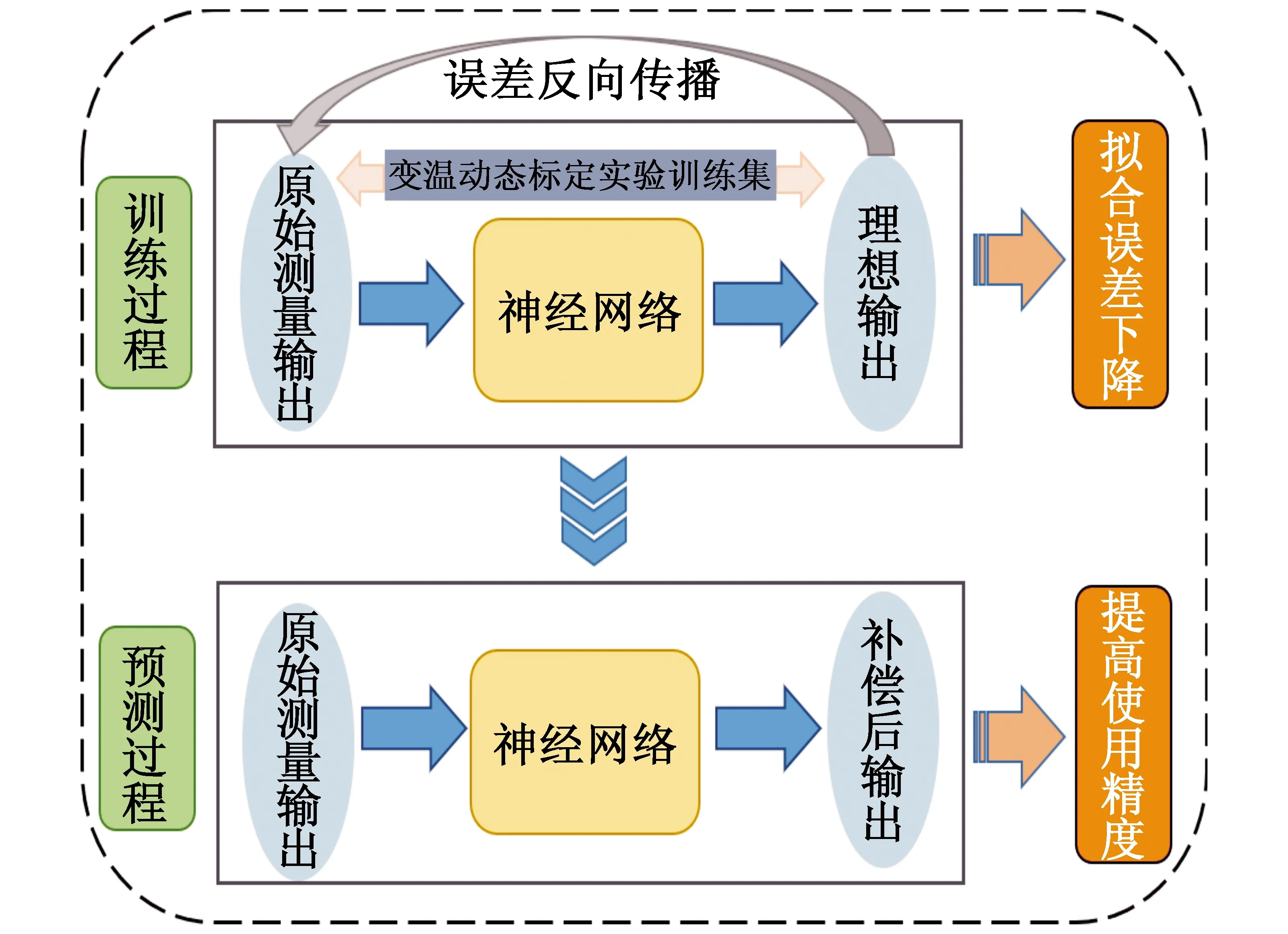
图3 整体工作结构示意图Fig.3 Schematic diagram of overall working structure

由于GRNN与RBFNN的层级结构是确定的，所以只需要确定合适的平滑因子和目标精度。通过多次实验选择在测试集上达到最优效果的平滑因子与目标精度即可。

深度神经网络的结构决定了其对复杂问题的学习能力，隐含层数越多，网络的特征学习能力越强，同时网络的复杂度也会增加、需要训练的参数增加、网络的训练速度下降。因此，需要针对具体问题选择合适的神经网络层数、神经元数目，损失函数、优化器、激活函数等。

本文针对的是回归问题，因此应该选择解决回归问题的损失函数，如均方误差、平均绝对误差等。为了避免循环神经网络中梯度消失与梯度爆炸问题，GRU与LSTM神经元的激活函数通常选择输出范围是[-1,1]的sigmoid函数和tanh函数。神经网络的层数、神经元数目、优化器通常需要进行多次实验，通过观察模型是否过拟合和测试集拟合精度，选择适合的参数。

2 实验设计与验证

2.1 标定实验流程

由于传统的标定实验采用的多位置翻转与角速率实验方法，无法充分地激励MIMU的误差特征，并且实际使用中MIMU的运动通常是动态连续的。因此本文设计了MIMU的整体动态标定实验方法。

实验设备采用TBL-3302-CT三轴带温箱位置速率转台。实验流程如下。

首先，通过转接工装将MIMU固定在内环转台上，使用直流稳压电源对MIMU供电，预热10 min。

然后，控制转台内环以0.01 (°)/s2的角加速度在1 (°)/s到-1 (°)/s之间均匀变化，控制转台中环以0.1 (°)/s2的角加速度转动，在10 (°)/s到-10 (°)/s之间变化，控制转台外环以1 (°)/s2的角加速度在100 (°)/s到-100 (°)/s之间均匀变化，同时控制温箱温度在-25℃～40℃之间变化。

最后，重复上述转动与温箱控制，采集三轴带温箱转台与MIMU的数据并保存。

上述实验达到了对三轴陀螺仪与三轴加速度计的动态连续激励，有利于激发出MIMU的误差特征，包括加速度与角速度的耦合误差、温度误差、安装误差等。

2.2 实验结果对比

实验使用自主研发的微惯性测量单元，其中集成了三轴陀螺仪、三轴加速度计和温度传感器，数据采集频率为200 Hz。

为了验证神经网络模型补偿效果进行对比，对MIMU进行24位置翻转实验，采集3 min的输出数据，进行角速率实验，对每个轴采集200～-200 (°)/s转速区间22个速率点的整周数据，使用传统的标定模型对其进行拟合。

传统模型拟合参数如表1和表2所示。

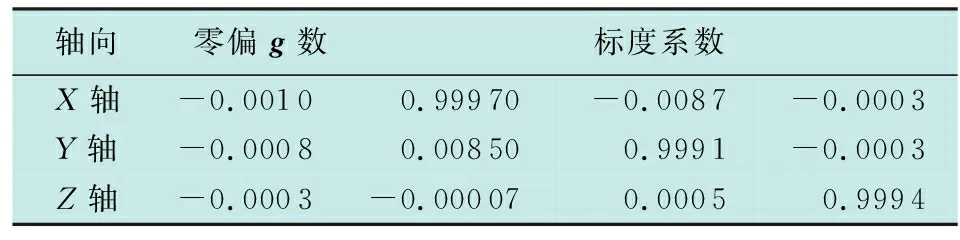
表1 加速度计标定系数Table 1 Calibration coefficients of accelerometer

表2 陀螺仪标定系数Table 2 Calibration coefficients of gyroscope

根据动态标定实验采集到的数据建立训练集与测试集，使用训练集对神经网络进行训练。通过测试集对训练后的神经网络性能进行测试，根据测试结果对神经网络的结构参数进行调整优化。

为了充分地进行对比，本文使用了RBFNN，GRNN，GRU，LSTM多种神经网络进行建模与补偿。通过多次测试优化，确定GRNN的平滑因子为0.07，目标精度为1E-4； RBF神经网络平滑因子为60，最大神经元为30，目标精度为1E-5。根据经验，通常3层循环神经网络隐含层即可解决大多数问题。通过测试对比，确定GRU隐含层神经元数目为60，损失函数为均方差，优化器为Nadma，训练步数为4000，隐含层激活函数为tanh，循环步的激活函数为Sigmoid。LSTM神经网络的设置与GRU相同，同样的条件下GRU需要训练的参数较LSTM下降24%。不同模型补偿后残差对比见表3。

表3 不同模型补偿后残差对比Table 3 Comparison of residuals after compensation of different models

通过表3可知，从残差平均值与标准差两方面而言，传统标定模型对误差的补偿效果有限，综合残差均值减少9.2%，标准差减少4.7%。浅层神经网络相较于传统标定模型而言补偿效果有一定提升，综合残差均值减少30%，标准差减少33%。其中，GRNN模型相对于RBF模型补偿效果更好，因为GRNN模型通过样本建立的高维模式层在样本量较少时能够达到更好的效果。循环深度神经网络能够实现精确的误差补偿，综合残差均值减少55%，标准差减少38%。其中，GRU神经网络与LSTM神经网络补偿效果相近，GRU相对于LSTM的训练参数少，进而训练速度更快，计算量少。

图4和图5分别为X轴陀螺仪和X轴加速度计输出补偿后的残差对比。

图4 X轴陀螺仪输出补偿后残差对比图Fig.4 Comparison of residual after X-axis gyroscope output compensation

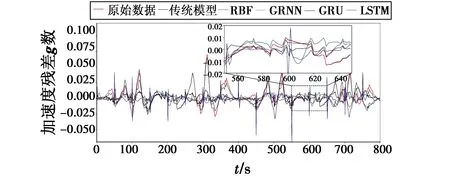
图5 X轴加速度计输出补偿后残差对比图Fig.5 Comparison of residual after X-axis accelerometer output compensation

通过图4和图5可知，深度循环神经网络可以较好地补偿误差，但是LSTM模型补偿后残差相对于GRU模型存在较多的毛刺，因此LSTM补偿后的残差标准差较大。

综上所述，浅层神经网络(RBFNN,GRNN)可以实现对多因素影响的MIMU误差特征建模与补偿，深度循环神经网络(GRU,LSTM)可以在此基础上进一步实现在时序特征上的误差补偿，其中，GRU模型相对于LSTM模型补偿后残差的标准差小，训练参数少，计算负担小。

3 结论

本文提出了MIMU测量输出与实际输出之间的神经网络模型，设计了动态标定实验流程，构建了多种神经网络模型并进行测试。相较于传统的标定模型而言，浅层神经网络由于考虑了多种因素在MIMU误差中的相互影响，误差补偿效果有所提升，深度循环神经网络通过对时序特征的学习，误差补偿效果进一步提高。实验结果表明，GRU模型可以实现对MIMU误差的深度补偿，不仅可以补偿确定性误差，对于具有时序性的随机误差也有一定补偿效果。随着半导体芯片算力的不断增强，本文方法在MIMU误差补偿领域中具有广阔的应用前景。