窗框结构对高速列车车窗隔声性能影响分析

周云龙，徐涆文，许天啸，肖新标

（西南交通大学 牵引动力国家重点实验室，四川 成都 610031）

高速列车速度的不断提升为车内的噪声舒适性提出了更高的挑战。而高速列车的噪声源并不少，一般来说，气动噪声和轮轨噪声是高速列车车内噪声最主要的两种激励方式，其传递路径也较为复杂[1-2]。车窗是高速列车不可或缺的组成部件之一，使用窗框和硬橡胶等元件与车体连接。在高速列车运行时，车外噪声源（轮轨噪声和气动噪声等）通过激振车窗等车体部件向车内辐射噪声[3]。而车窗是车外噪声传递进来的一条关键路径，需要被注意以及关注。因此，研究车窗的隔声对改善车内声舒适度是极为必要的。

目前，国内外对高速列车车窗的声振特性研究相对较少[4-11]。首先，张玉梅等[4-5]建立了高速列车车窗双板空腔模型，在基于波动法和模态叠加法的情况下，讨论了双板不同厚度比时隔声量的最佳配比以及空气空腔阻尼对高速列车车窗隔声量的影响。并基于当前参数的调查，得到了最优隔声量工况。Yang[6]通过声压法和声强对单层玻璃自适应边界层（Automatically Matched Layer，AML）模型进行了验证，并基于此建立双板空腔结构隔声模型，赋予中间空腔的属性从空气转变成氩气，并结合遗传算法对双板几何参数进行了优化。石广田等[7]和徐郑骁[8,11]对空腔为真空的车窗进行了板件厚度、声桥长度和真空度属性等不同参数的调查，并提出在高频段区域一种电致变色软膜车窗玻璃的隔声性能优于PVB夹层玻璃。朱荟吉等[9]对理想边界条件和一般边界条件下车窗的隔声的影响进行了研究，并提出相应车窗与车体安装刚度理想值。PAN等[10]将湍流边界作为激励源，分别将双侧玻璃厚度、空腔厚度和空腔阻尼损失因子作为不同参数讨论了高速列车车外表面脉动压力对车窗的隔声性能的影响。XU等[11]采用统计能量法（Statistical Energy Analysis，SEA）分别对单层玻璃、夹层玻璃和双层中空玻璃车窗进行了隔声性能比较，在不考虑漏声的情况下，将铝合金窗框和不同密封材料进行组合，研究了车窗与窗框之间的密封材料对车窗整体的隔声的影响。

然而，从目前对高速列车车窗的声振特性研究来看，对车窗的隔声性能研究基本是忽略了窗框，只考虑了“板－空腔－板”结构的研究思路。窗框作为连接车窗与车体结构的部件之一，却少有人将其考虑进车窗并进行整体的声振特性研究。因此，研究窗框对高速列车车窗整体性能的影响是很有必要的。因此，本文以高速列车车窗作为研究对象，基于有限元－统计能量法（FE-SEA）混合法理论，对高速列车车窗在有窗框与无窗框的两种情况下分别做隔声性能分析。同时引入一种新型Mn-Cu阻尼合金材料属性赋予窗框结构，将阻尼合金框车窗与传统铝合金框车窗的隔声性能进行比较分析，阐述两种不同材料属性窗框对整体车窗的隔声性能的影响，为接下来高速列车车窗的窗框结构和材料的优化设计提供些许参考。

1 计算理论

对于声振耦合问题，目前主要有三种处理方法：有限元法（FEM）、统计能量法（SEA）和边界元法（BEM）。FEM和BEM作为确定性子系统的分析方法，在高频段的计算结果表现并不是很好；SEA是一种非确定性子系统的分析方法，拥有统计性质的SEA在高频段的计算结果与实际拟合良好。因此，这三种方法在一定程度上各自在高频和低频计算中有着缺陷。为了求解复杂声振系统的整体平均响应，Shorter和Langley[12-13]提出了一种基于波动法的FE-SEA混合方法。

1.1 FE-SEA混合法

本文采用FE-SEA混合方法对高速列车车窗结构的隔声特性进行研究，此法是把整个车窗结构划分为用FEM描述的确定性子系统以及用SEA法描述的非确定性子系统。

建立结构子系统的运动方程为：

式中：Dtot为结构子系统的总动刚度矩阵；q为结构子系统的自由度；f为作用于子系统上的外部载荷列向量；m指在整个系统中SEA子系统的总数量；为第m个SEA子系统在确定性边界处对FE子系统所施加的混响场载荷，Pa；为车窗结构子系统本身存在的动刚度矩阵与各个SEA子系统的直接场总动刚度矩阵的总和。

对式（1）求解后，确定性子系统的动态位移响应方程为：

接着对SEA子系统建立能量平衡方程，输入功率流计算如下：

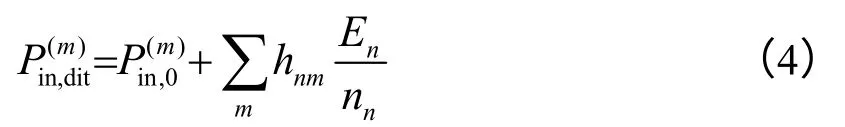
此时在子系统中的输入功率流等效于子系统输出功率流与自身耗散功率流之和，满足能量平衡方程：

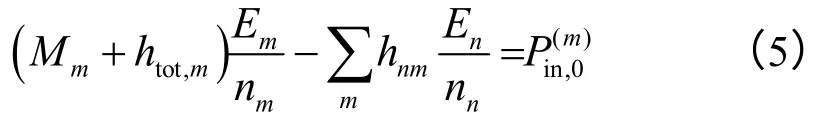
式中：Mm为模态重叠因子；htot,m为混响场输出能量第m个子系统的模态能量密度。

整个FE-SEA模型中各个统计能量子系统的响应结果以及有限元子系统的位移响应结果即可通过以上相关子系统的能量平衡方程整理获得。

1.2 隔声量

整个车窗结构的隔声量为[14]：

式中：TL为整个车窗结构的隔声量，dB；Ac为向高速列车车窗外侧辐射能量时的辐射面积，m2；ω为角频率，rad·s-1；c0为空气中的声速，m·s-1；ns为整体模态密度；ηsr,tot为发声与接收两侧之间的有效耦合阻尼损耗因子。

2 车窗隔声建模及窗框阻尼损耗因子测算

2.1 车窗预测模型

无窗框的高速列车车窗整体结构较为简单。在此之前车窗的不少研究都是从板结构的研究发展而来。因此，基于FE-SEA混合法以及双板空腔理论，在ESI VA One中建立了高速列车无窗框结构车窗的隔声预测模型。计算模型如图1所示。

由图1可见，高速列车车窗与两个半无限流体子系统连接，而半无限流体子系统被视作车窗内外两侧的空气层，其中车窗外表面一侧与混响声源相连接，相当于在车窗外表面的外侧施加了一个混响声源。而无窗框车窗由四部分组成，分别是外侧玻璃、空气夹层、硬橡胶和内侧玻璃。外侧玻璃和内侧玻璃的平面尺寸大小一致，为650 mm×700 mm。玻璃厚度有所不同，其中外侧玻璃为双层结构，最外侧厚度为5 mm，另外一层厚度为4 mm；内侧玻璃虽然也是双层结构，但是两层厚度均为3.5 mm。硬橡胶壳单元厚度为5 mm，通过共节点的方式将内外两侧玻璃连接在一起。而空气夹层厚度为16 mm，利用声腔进行处理，并添加相应的阻尼损耗因子。根据文献[5]可知，将车窗内空腔阻尼损耗因子η0取值为0.05，两侧玻璃的阻尼损耗因子η1,2取值为0.005。无窗框车窗结构的其他材料参数如表1所示。

表1 车窗结构材料参数

图1 高速列车车窗隔声预测模型

2.2 阻尼损耗因子

2.2.1 识别原理

Mn-Cu阻尼合金作为一种新型材料，材料属性的合理配比另其阻尼性能得到了较好的提升；经过常温条件下的塑性变形及热处理后，合金具有良好的机械性能；经过特殊保温处理，表面能够形成结构完整且致密的氧化膜，表现出良好的耐蚀性。在探究车窗隔声特性之前，有必要去获得窗框材料的阻尼损耗因子数据。

阻尼损耗因子是统计能量分析子系统中的主要参数之一。本文采用瞬态衰减包络线法[15]进行了相关测试。此方法基于测量系统或者结构受到脉冲时的衰减率进行测算。

根据单频模态位移响应，得：

式中：f为频率，Hz；η为阻尼损耗因子；t为时间，s；系统中能量与峰值振幅的平方成正比，t1、t2分别为两个峰值幅值的时间节点；G1、G2分别为在t1与t2之间的衰减斜率，与系统的峰值响应幅值有关。

系统响应曲线的衰减率为：

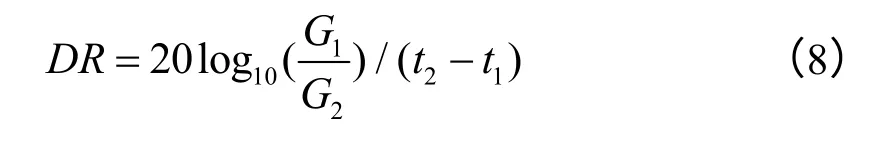
此时频带平均的阻尼损耗因子可表示为：

2.2.2 试验与数据获取

接下来是车窗的力锤敲击试验。为了使隔声计算结果更为准确，准备了两种窗框材料，基于此试验条件，对两种材料的阻尼损失因子进行了测算。

试验测试如图2所示，将窗框上布置好的加速度传感器作为响应点，随后用力锤敲击窗框加速度传感器附近的测点作为激励点，在每个测点位置敲击3次，保证试验的重复性以减少误差。试验采用的测试设备有B&K 8206-002力锤、B&K 4520Z加速度传感器、B&K 3053-B-120 LAN-XI 数据采集系统。试验过程中，采样上限频率设置为3200 Hz。

图2 窗框阻尼损耗因子实测图

经过对不同窗框材质的车窗分别进行敲击测试，得到了0～3200 Hz范围内的模态阻尼，并利用最小二乘法获取插值拟合曲线，如图3所示。其中铝合金窗框的阻尼损耗因子变化趋势是先增大后减小，在1000 Hz处达到最大值，为0.033；随着频率的增加逐渐降低并在2500 Hz以后趋近于0.01。与传统铝合金材料相比，阻尼合金窗框材料的阻尼损失因子变化趋势就比较复杂，在250～1250 Hz的中频和2500 Hz之后的高频有着较大提升，当频段接近630 Hz，此时阻尼损失因子最大差值可达到0.02，其他频段与铝合金接近。

图3 窗框阻尼损耗因子

3 窗框对车窗隔声性能影响分析

3.1 窗框结构影响

第2节建立了高速列车无窗框车窗隔声预测模型，但是窗框结构并不是单一的板件。因此，若要将窗框结构考虑进整个车窗中，那么需要在原基础上按照实际尺寸对车窗结构进行整体建模。

如图4所示，为了能更加贴合实际，车窗玻璃与硬橡胶尺寸基本与第2节描述一致。窗框结构由于结构复杂，做了相应的简化处理。模型中窗框结构为传统铝合金，其材料属性如表2所示。

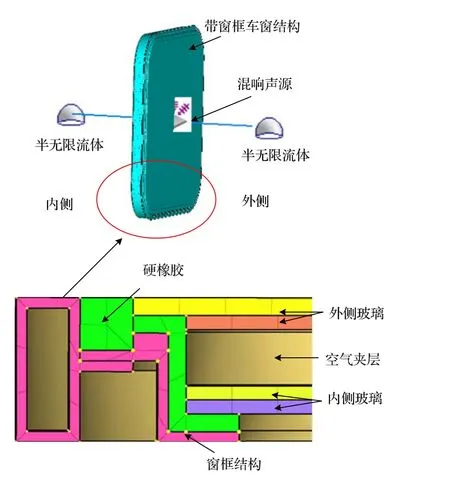
图4 带窗框结构的整体车窗模型

表2 窗框材料参数

本节中采取控制变量的方式研究了窗框结构对车窗隔声量的影响。计算结果如图5所示。

由图5可见，无窗框结构车窗整体计权隔声量Rw1＝33.6 dB，而铝合金窗框结构车窗整体计权隔声量Rw2＝35.7 dB，整体计权隔声量提升了2.1 dB；有窗框结构对100～160 Hz以及1000～2500 Hz之间车窗隔声量有着明显的提升。从无窗框结构车窗三分之一倍频程中心频率来看，100 Hz时有无窗框结构使车窗整体隔声量出现了较大的插值，这与对应的模态频率相关，此频段下无窗框结构车窗出现了隔声低谷。由此可见，窗框结构对车窗100 Hz左右的低频和1000～2500 Hz之间的中高频隔声性能有着较好的提升，且整体隔声性能也得到了不错的优化。因此，窗框结构能够对车窗隔声性能带来不可忽视的影响。

图5 窗框结构对车窗隔声影响

3.2 窗框材质影响

窗框结构使整体隔声效果得到了提升。既然窗框结构对车窗隔声性能具有一定的优化效果，本节将引入另一种不同于传统铝合金的窗框材料，探究不同的窗框材料对车窗隔声性能的影响。这种材料为Mn-Cu阻尼合金，其材料属性如表2所示。

在相同的计算条件下，进行仿真预测100～3150 Hz隔声性能，得到不同窗框材料对车窗整体隔声性能对比，如图6所示。

根据图6可以看出窗框材质对车窗隔声影响，从整体来看，铝合金窗框结构车窗整体计权隔声量Rw2＝35.7 dB，而阻尼合金窗框结构车窗整体计权隔声量Rw3＝37.6 dB，整体计权隔声量提升了1.9 dB。

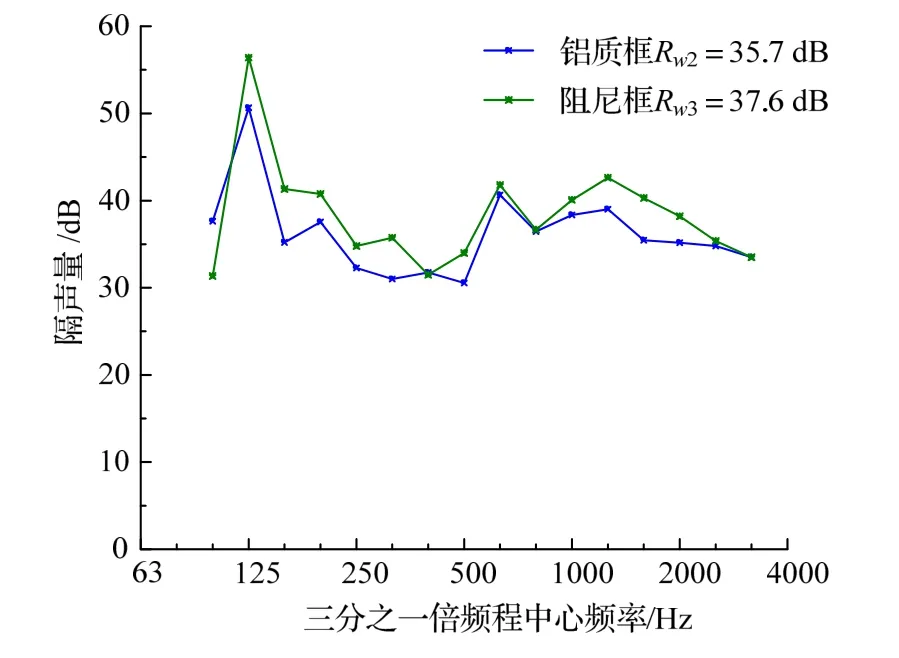
图6 窗框材质对车窗隔声影响

从图7中可以更直观的了解到阻尼合金窗框车窗整体隔声量在各频段中的差值。100 Hz时阻尼合金窗框车窗隔声量低于铝合金窗框车窗6.2 dB，此时阻尼合金模态频率为98.2 Hz，因此出现了隔声低谷；同时在100 Hz处阻尼合金材料的阻尼损耗因子低于铝合金材料，从而导致出现在100 Hz隔声量有所降低的情况。除了100 Hz之外，其余频段的隔声量要么与铝合金窗框车窗接近，要么优于铝合金窗框车窗。并在160 Hz、315 Hz、500 Hz和1600 Hz等典型峰值处出现了较大的差值峰值，分别为6.1 dB、4.7 dB、3.4 dB和4.9 dB。由此可见，将窗框材料从原有的铝合金替换成Mn-Cu阻尼合金能够有效提高车窗整体的隔声性能，具有一定的参考意义。

图7 窗框材质致车窗隔声量差值

4 结论

基于FE-SEA混合法，本文以高速列车车窗为研究对象，在混响声场中研究了窗框对车窗整体隔声性能的影响；并引入一种新的窗框材料Mn-Cu阻尼合金，进一步改善了车窗整体隔声性能，结论如下：

（1）与铝合金材料相比，阻尼合金材料的阻尼损失因子在250～1250 Hz的中频和2500 Hz之后的高频有着较大提升，当频率接近630 Hz，此时阻尼损失因子最大差值可达到0.02，其他频段与铝合金接近；

（2）窗框对车窗在100 Hz左右的低频和1000～2500 Hz之间的中高频的隔声性能的提升明显。无窗框车窗整体计权隔声量Rw1为33.6 dB，而铝合金窗框车窗整体计权隔声量Rw2为35.7 dB，整体计权隔声量提升了2.1 dB；

（3）当窗框被赋予Mn-Cu阻尼合金材料后，与传统铝合金窗框车窗相比，除了100 Hz，全频段的隔声性能都有良好的改善。阻尼合金窗框车窗整体计权隔声量Rw3为37.6 dB，整体计权隔声量提升了1.9 dB。