地铁设备吊挂梁瞬态冲击仿真及试验研究

张 宜，韦海菊

（中车南京浦镇车辆有限公司，南京 210031）

吊挂梁用于将高压箱、变流器、制动模块等设备连接到底架边梁上。吊挂梁若发生断裂或疲劳破坏会严重影响地铁安全性，因此建立准确预测结构薄弱区域的计算模型，是后续进行强度评估和优化的前提。

目前设备冲击仿真常用静力学方法简化计算而不是瞬态方法，同时试验验证采用定性验证而非定量验证。例如：刘峰［1］使用瞬态法计算变流器冲击强度，但只做了定性试验验证；徐聪［2］使用静力学和瞬态方法计算了高压箱冲击强度，发现2 种方法结果差异较大，但未进行试验验证；黄磊杰［3］使用静力学方法对变流器机箱进行冲击强度评估和优化。

文中使用模态叠加法计算了吊挂梁瞬态冲击的动态响应，并用试验定量验证了模型的准确性，最后对吊挂梁型材进行了减重优化。基本流程如图1 所示。

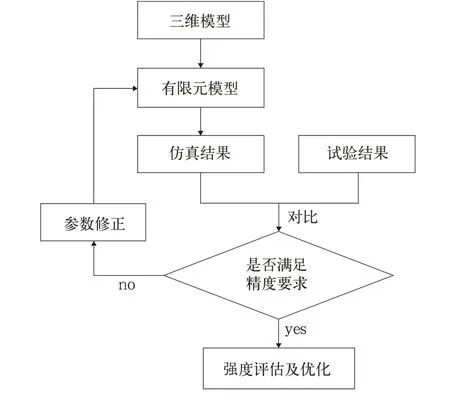
图1 基本流程图

1 模态叠加法基本理论

模态叠加法求解瞬态冲击问题，首先求解系统的各阶振型和对应的模态频率，利用振型和模态频率将运动平衡方程转换成单自由度系统振动方程并求解动态响应，然后将每个振型响应结果进行线性叠加，得到原来系统的动态响应［4-5］。

在冲击载荷作用下，多自由度系统运动微分方程可以表示为式（1）：

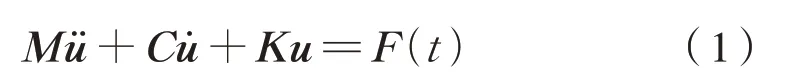
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F（t）为外载荷矩阵；u¨ 为加速度矩阵；u˙为速度矩阵；u为位移矩阵。

由式（1）得到系统的n阶固有频率ω1，ω2，…，ωn和n阶振型φ1，φ2，…，φn。

位移矩阵可表示为式（2）：

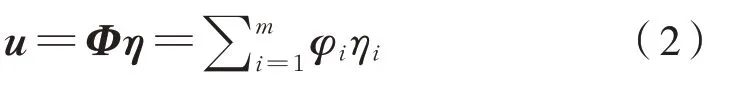
式中：Φ为振型矩阵；η为模态坐标向量；φi为振型向量；ηi为模态坐标。

将式（2）带入式（1），并在方程两边同乘振型矩阵的转置φT得到式（3）：

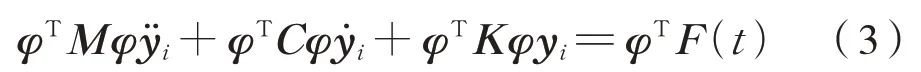
对式（3）进行求解得到主坐标下的响应，再变换得到物理坐标下的响应。通常高阶模态对响应的影响很小，所以在满足工程精度的前提下对高阶模态进行截断处理，模态截断的频率通常为最高激励频率的3～5 倍。

2 吊挂梁瞬态冲击仿真

2.1 材料模型及参数

选择MAT1 材料模型，材料的泊松比、弹性模量和密度等参数见表1。

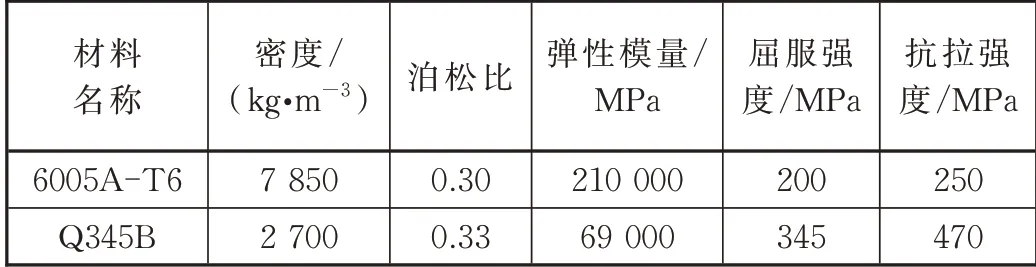
表1 材料力学性能参数

2.2 冲击载荷

吊挂梁设计应满足IEC 61373-2010《机车车辆设备冲击和振动试验》标准的要求，该标准规定直接安装于车体下的设备属于1 类A 级设备［6］，冲击脉冲信号如图2 所示。

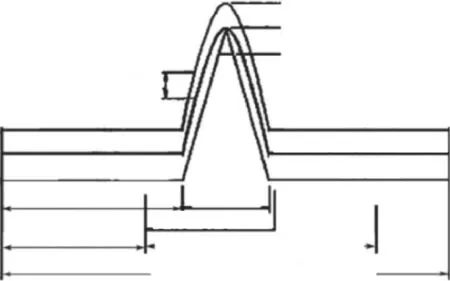
图2 半正弦冲击脉冲信号控制图

对应的冲击加速度函数应满足式（4）：

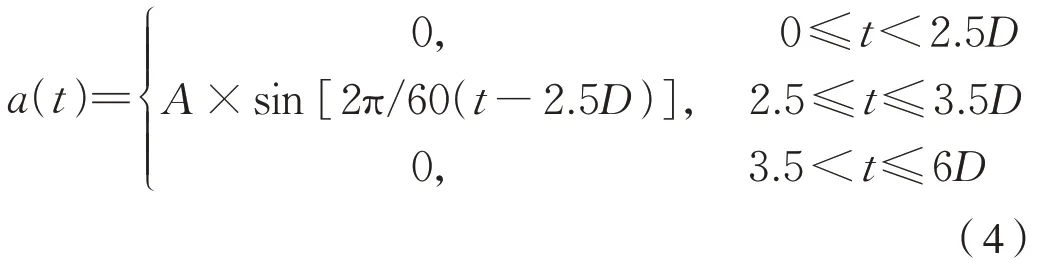
式中：A为峰值加速度，X、Y和Z方向对应的峰值加速度分别为±50 m/s2、±30 m/s2和±30 m/s2；D为冲击时间30 ms，由于X和Y方向是对称的，且Z正方向比负方向恶劣，文中只计算和对比正方向结果。

2.3 有限元模型

有限元模型包括吊挂梁和吊挂座、配重、工装3 个部分。吊挂梁材料为铝合金6005A-T6，吊挂座材料为Q345，通过铆钉与吊挂梁连接，共重85 kg；配重材料为Q345，用于模拟车下吊挂设备，重775 kg；工装材料为Q345，用于连接吊挂梁和试验台，重1 811 kg。以上结构均采用壳单元进行离散，各个部分的有限元模型如图3 所示。

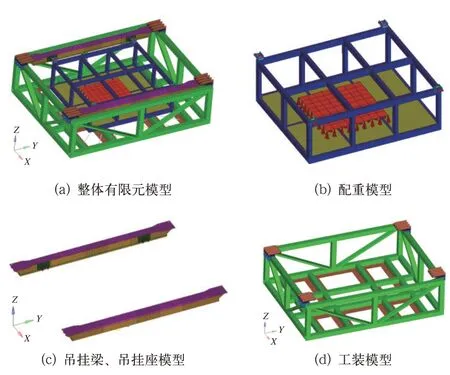
图3 有限元模型

2.4 仿真结果

3 个方向的冲击响应Mises 应力云图及响应曲线如图4～图9 所示。

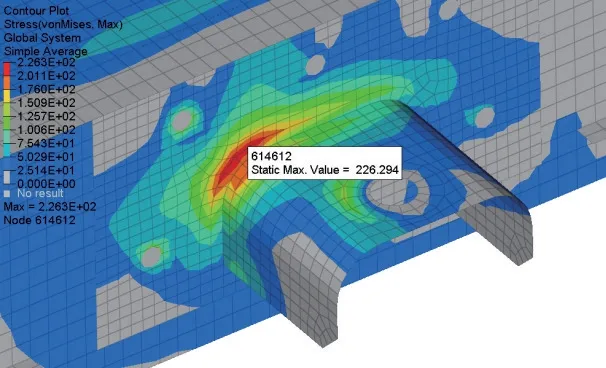
图4 X 方向冲击Mises 应力云图

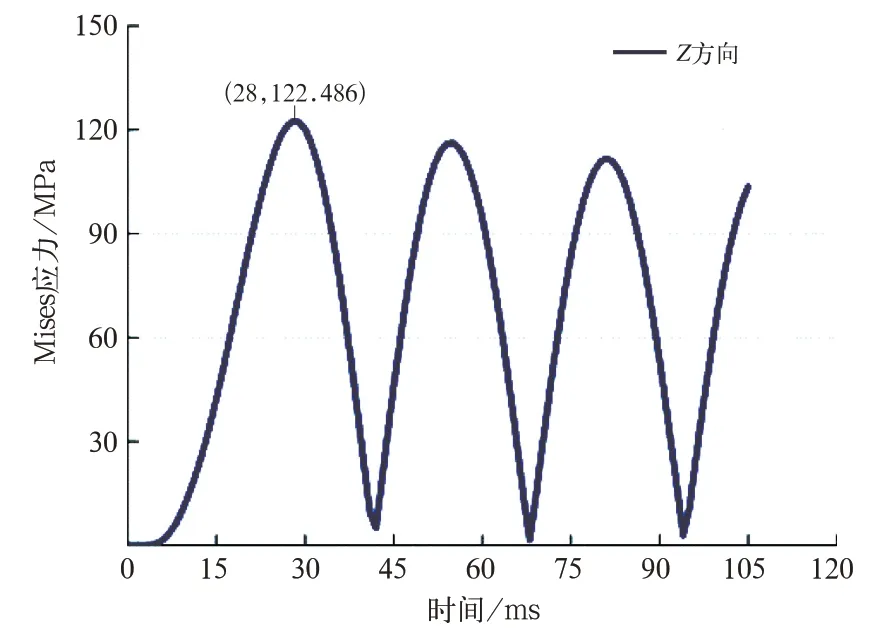
图9 Z 方向冲击最大位置Mises 应力曲线

X方向冲击的最大等效应力位于吊挂座焊缝根部，在第1 个响应周期的26 ms 时Mises 应力最大，为226.294 MPa，小于Q345B 的屈服强度。在之后的响应周期，由于结构阻尼的作用，振动不断衰减。

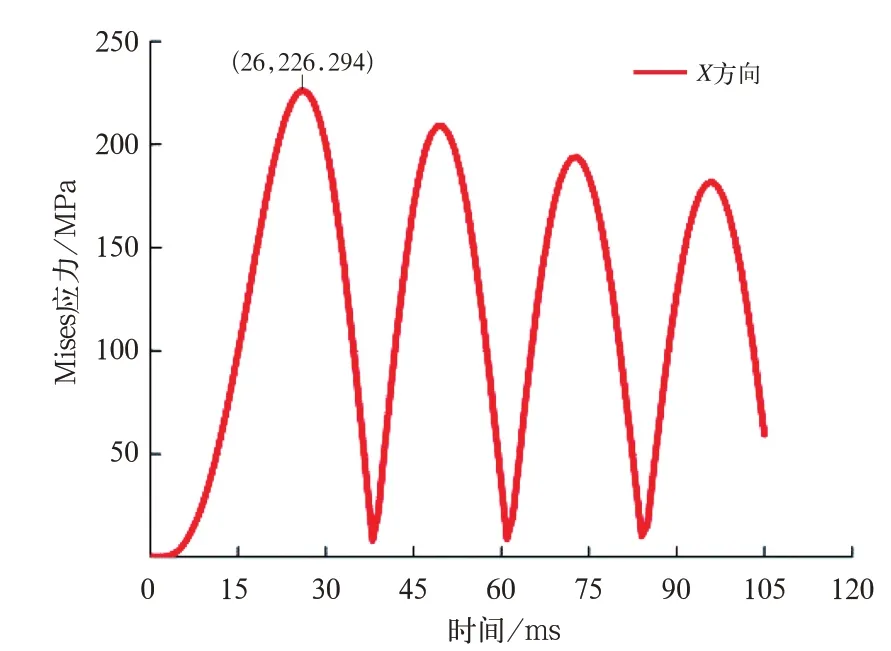
图5 X 方向冲击最大位置Mises 应力曲线

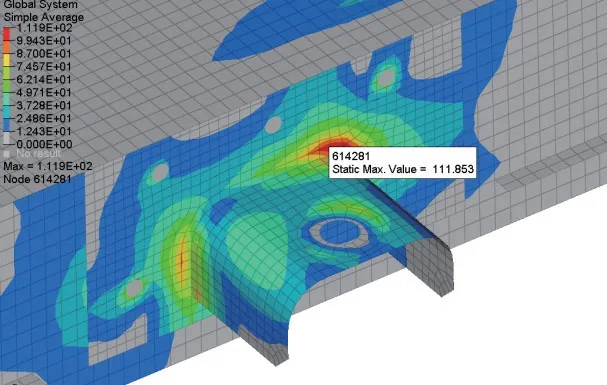
图6 Y 方向冲击Mises 应力云图

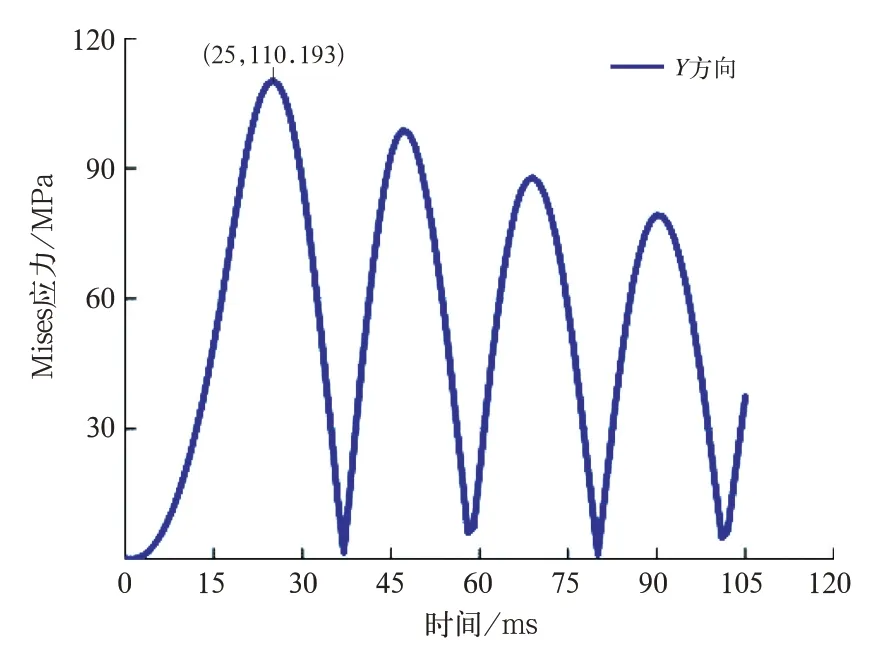
图7 Y 方向冲击最大位置Mises 应力曲线

Y方向冲击的最大等效应力位于吊挂座焊缝根部，在第1 个响应周期的25 ms 时Mises 应力最大，为110.193 MPa，小于Q345B 的屈服强度。

Z方向冲击的最大等效应力位于吊挂座焊缝根部，在第1 个振动周期的28 ms 时Mises 应力最大，为122.486 MPa，小于Q345B 的屈服强度。

由仿真结果看出3 个方向最大应力最大值都出现在第1 个响应周期内，位于吊挂座焊缝根部，该位置附近为高应力区域，可以作为试验布置应变测点的参考点。

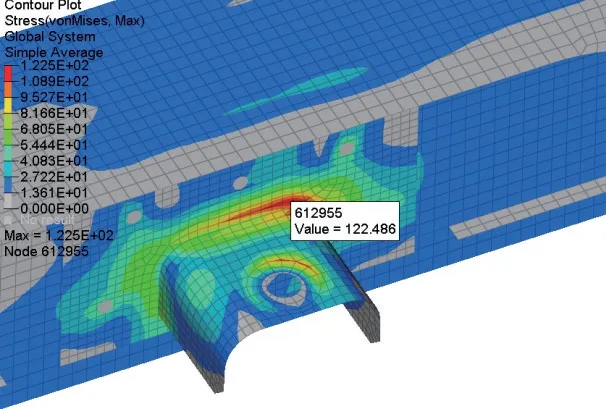
图8 Z 方向冲击Mises 应力云图

3 试验验证

3.1 试验设备

用于试验的吊挂梁及相关部件已安装到试验台上，如图10 所示，试验主要设备见表2。

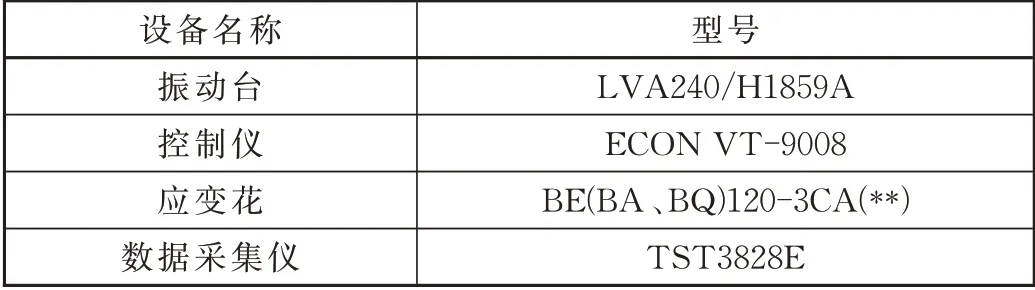
表2 冲击振动试验设备

图1 0 吊挂梁冲击振动试验台

根据2.4 节的仿真结果在吊挂座S3处布置1 个应变花，值得注意的是，试验时布置的应变测点并非是最大响应所要出现的位置，而是用于监测冲击过程的应变响应及结果验证，测点布置如图11所示。

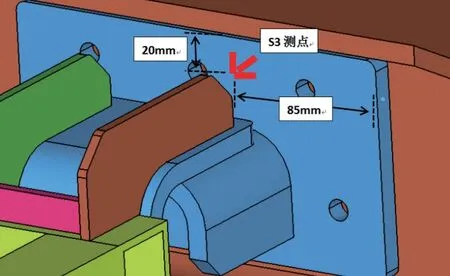
图1 1 应变花贴片位置

3.2 对比方式

方式1：0o、45o、90o应变花采集3 轴应变，根据式（5）～式（7）计算出主应力，再根据式（8）计算出等效应力，跟仿真相同位置的Von Mises 应力对比。

方式2：0o、45o、90o应变花采集3 轴应变，选取最大通道的方向应变，根据式（7）计算出方向应力，跟仿真相同位置的方向应力对比。

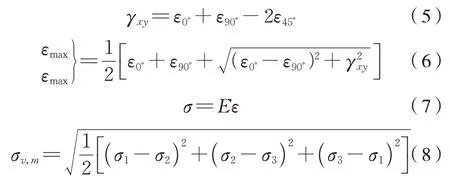
式 中：γ为 切 应 变；ε为 正 应 变；E为 弹 性 模 量；σv，m为等效应力；σi(i=1，2，3)为第i主应力。

在实际工程中，对于碳钢和铝合金材料，由等效应力判断是否超出许用应力，而应力的正负方向则需要比较方向应力，因此先用方式1 对比最大等效应力，再用方式2 对比单通道的方向应力。

3.3 仿真与试验结果对比

X、Y、Z3 个方向的试验和仿真Mises 应力及方向应力响应曲线对比如图12～图17 所示。

图12～图17 曲线表明，受到冲击后，仿真与试验的等效应力响应曲线在第1 个周期内有较高的一致性，应力的大小、方向和变化趋势基本吻合。

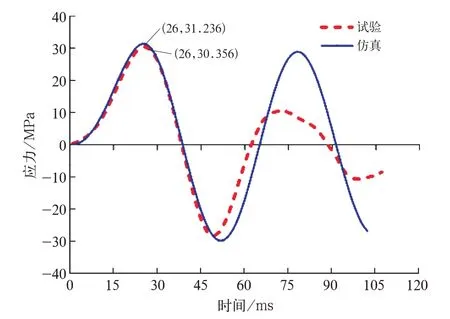
图1 7 Z 方向冲击的方向应力对比

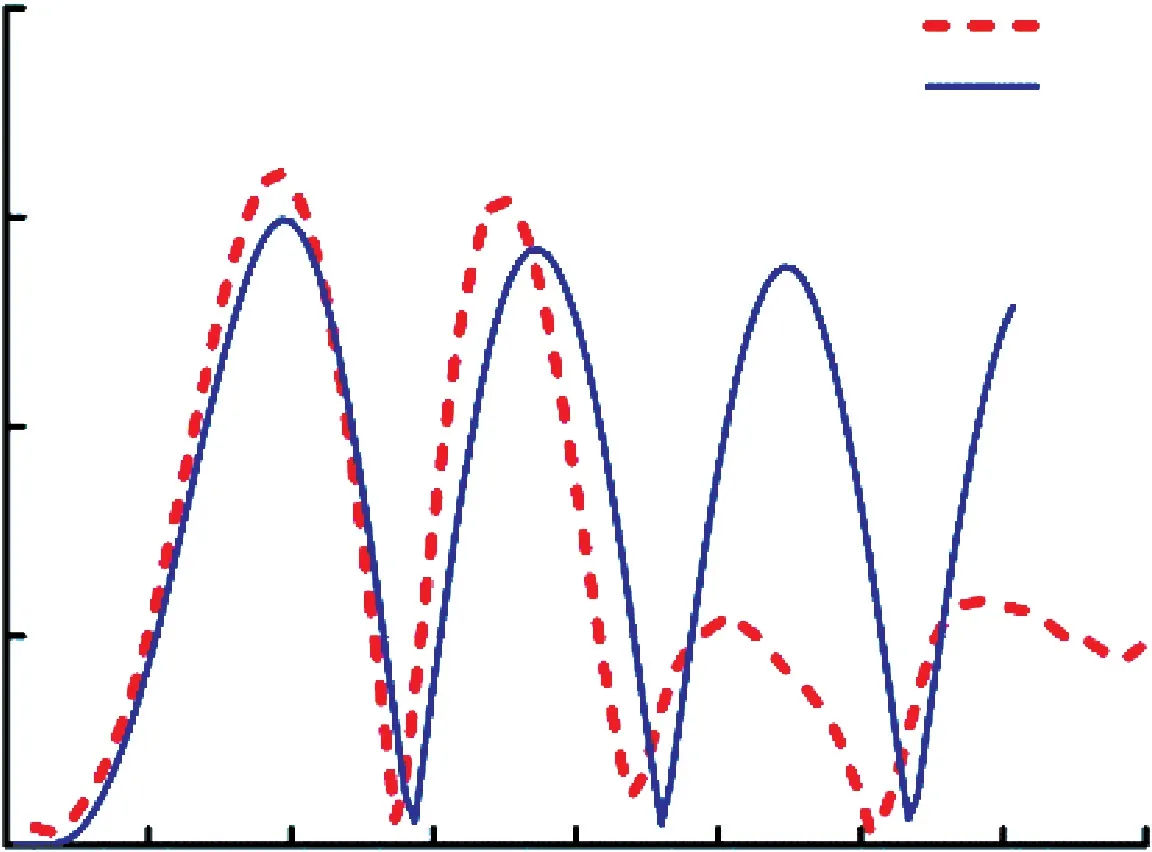
图1 6 Z 方向冲击的Mises 应力对比

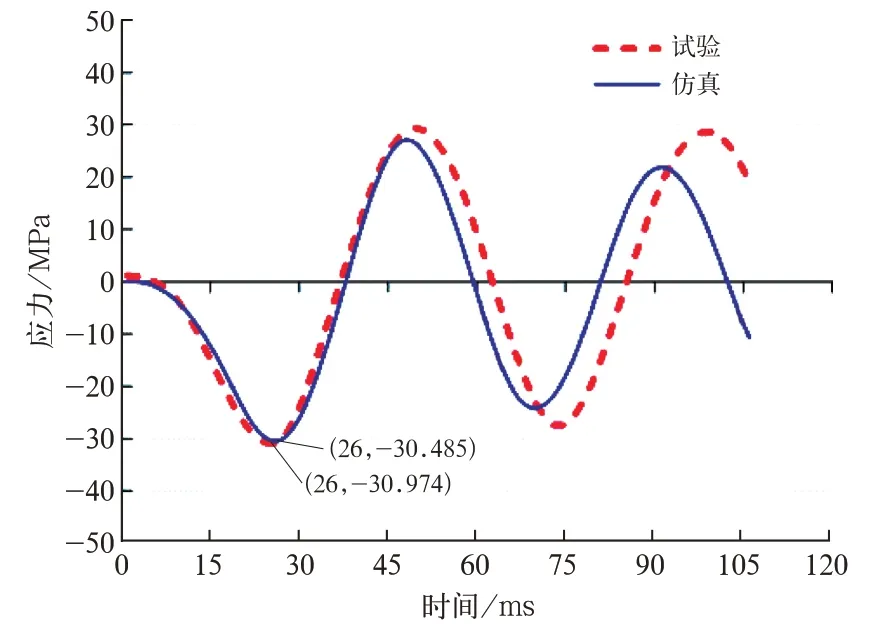
图1 5 Y 方向冲击的方向应力对比

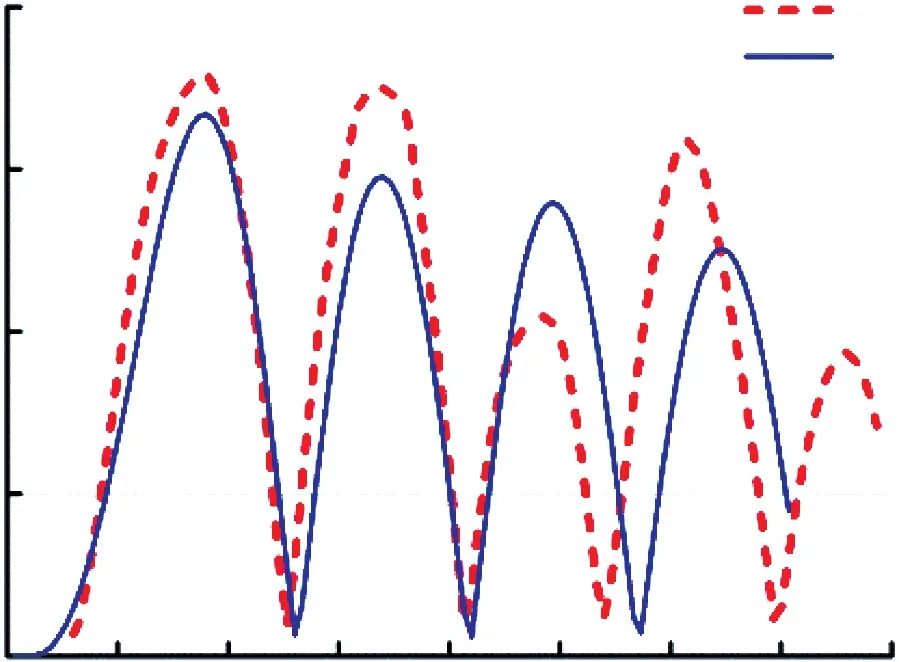
图1 2 X 方向冲击的Mises 应力对比

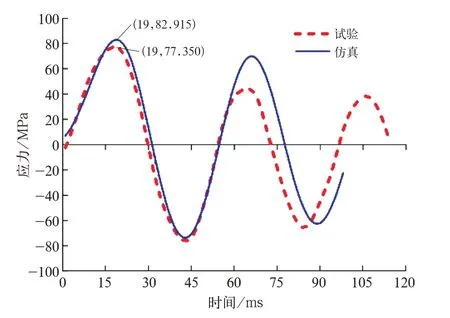
图1 3 X 方向冲击的方向应力对比

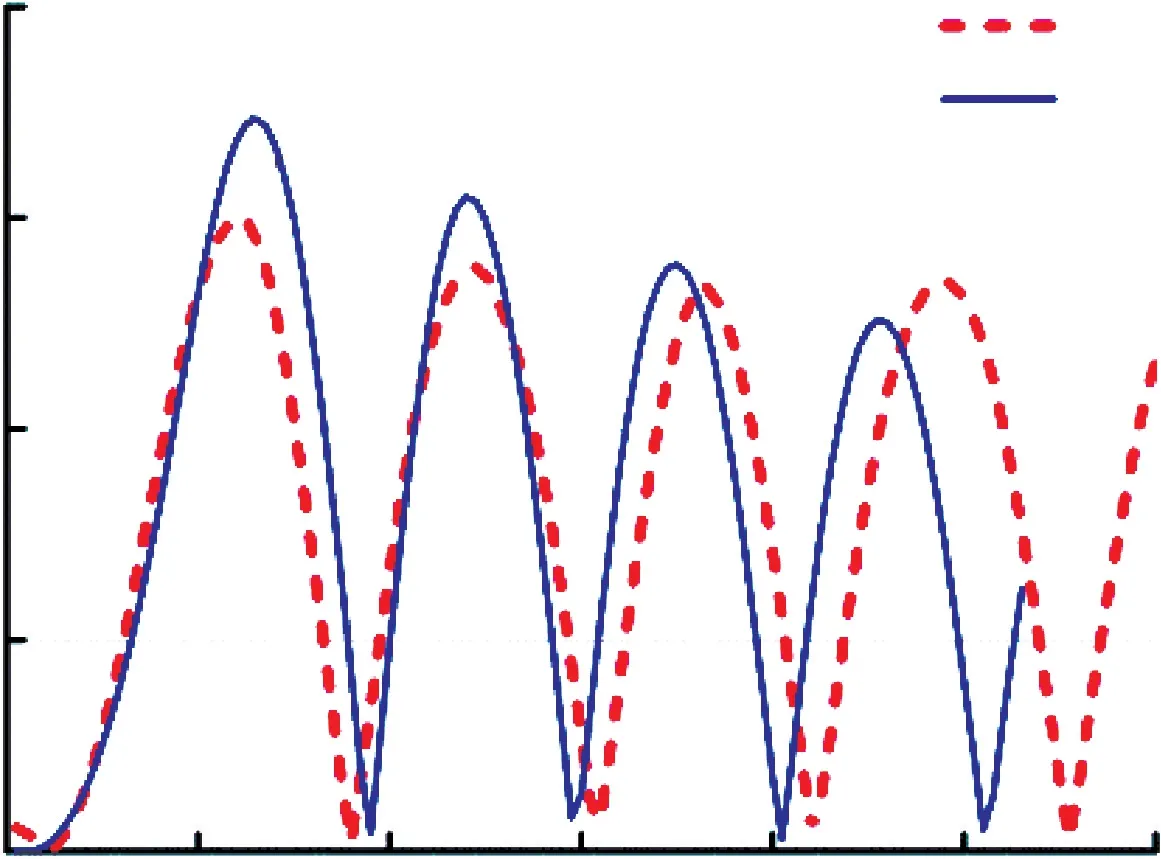
图1 4 Y 方向冲击的Mises 应力对比

X方向冲击时，测点方向应力由正到负，即先受拉后受压。

Y方向冲击时，测点方向应力由负到正，即先受压后受拉。

Z方向冲击时，测点方向应力由负到正，即先受压后受拉。

将仿真和试验结果汇总见表3，可知第1 个响应周期内，最大误差出现在Y方向冲击的等效应力，为11.827%，满足工程要求。

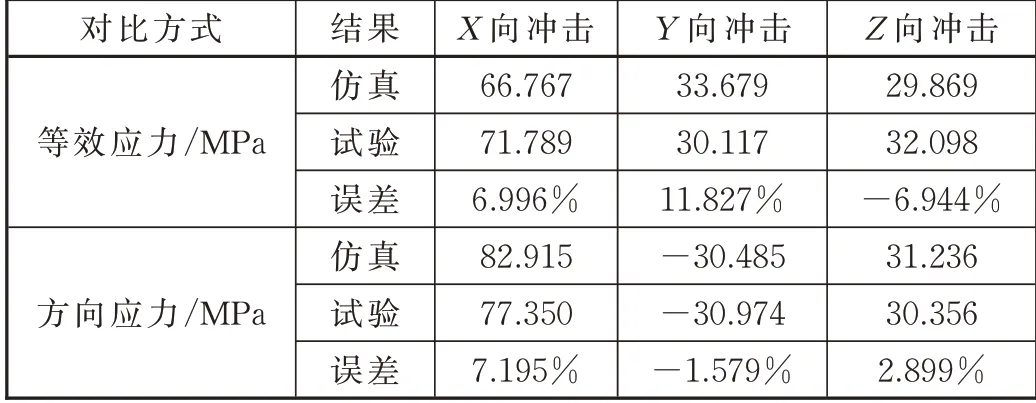
表3 仿真相对于试验的误差

对于第1 个响应周期后的时间，仿真与试验有较大误差，这可能与结构的阻尼比有关，文中采用了默认的阻尼比进行计算。

4 结构优化

4.1 型材参数优化

由第3 节可知，最大应力在安装座区域，而铝合金型材梁整体应力远小于材料的屈服强度，有一定的减重优化空间。

对结构优化过程中要考虑模态频率变化可能引起的共振现象。城轨铝合金车体整备状态下一阶垂弯模态一般在7～11 Hz 之间，为了与车体和转向架频率充分隔离，应保证吊挂梁结构一阶垂弯频率不小于1.4 倍车体一阶垂弯频率［7］，即不小于15.4 Hz。

使用Optistrct 对型材进行参数优化，需要建立吊挂梁结构参数优化模型，确定设计变量、约束函数和目标函数：

（1）设计变量：吊挂梁型材截面的厚度。

（2）约束函数：X、Y、Z方向冲击工况的最大应力≤200 MPa，一阶垂弯频率≥19 Hz。

（3）优化目标：质量（体积）最小。

型材截面的尺寸参数如图18 所示，将这7 个板厚尺寸参数化，原始厚度为：［T1，T2，T3，T4，T5，T6，T7］=［10，8，8，8，8，10，8］，每个变量变化范围为［3，10］，单位mm。

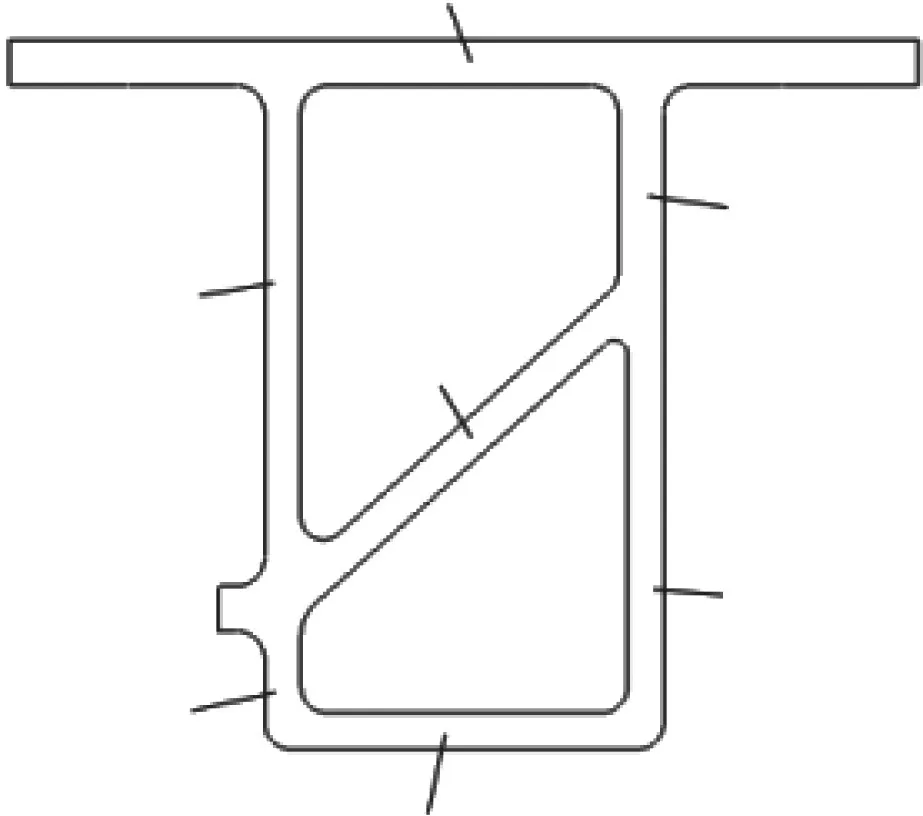
图1 8 型材截面尺寸参数

4.2 优化结果分析

优化后各个尺寸参数的结果如下：

［T1，T2，T3，T4，T5，T6，T7］=［9，8.8，10，10，5.6，4.1，4］

对比尺寸参数的变化可知，型材在有安装座的一侧板厚有所增加，而没有安装座的一侧板厚有所减小。厚度变化引起的响应变化见表4。

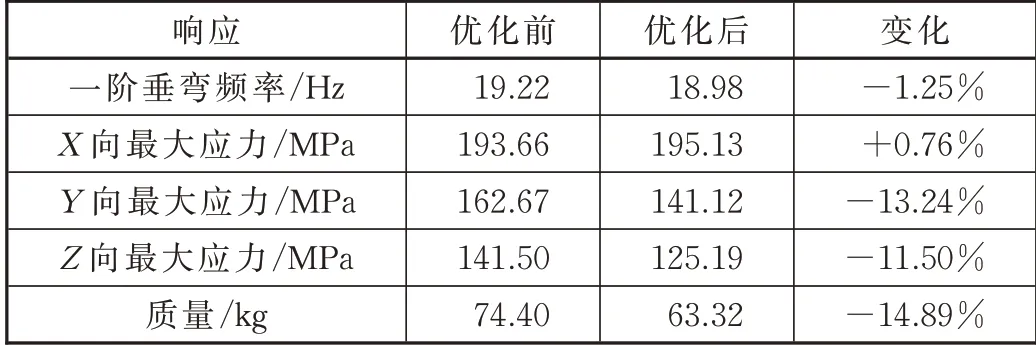
表4 优化前后各个响应的变化

分析表4 可知，优化后的3 个方向应力响应均小于材料屈服强度；一阶垂弯频率减小1.25%，略小于原始结构频率，但仍然满足要求；质量减小了14.89%，达到了明显的减重效果。

5 结 语

（1）文中建立了设备吊挂梁计算的有限元模型，采用模态叠加法对吊挂梁进行瞬态冲击仿真，获得了吊挂梁和吊挂座高应力区域，用于指导试验应变片贴片位置。

（2）对吊挂梁模型进行定量试验，分别对比了仿真和试验的等效应力和方向应力的响应曲线，仿真计算的应力大小、方向和变化趋势与试验有很好的一致性，表明建立的有限元模型的有效性。

（3）对吊挂梁型材结构进行参数优化，优化后的结构质量减小了14.89%，而一阶垂弯频率和冲击强度仍然满足要求，达到了轻量化的目的。为同类设备的冲击仿真、试验对标及优化提供了参考。