铁路货车车体疲劳台架试验仿真模拟的关键技术研究

赵尚超，王东坡，李向伟

（1 天津大学 材料科学与工程学院，天津 300350；2 中车齐齐哈尔车辆有限公司，黑龙江 齐齐哈尔 161002）

随着铁路货车载重增大及运行速度的提高，车辆载荷条件发生了较大变化，但由于设计过程中缺少经验及试验条件不完善等原因，一些铁路货车产品发生了疲劳失效的事故［1-3］。针对铁路货车核心承载结构的全尺寸车体的全寿命周期抗疲劳性能评价，由于缺少大型试验装备，一直没有形成有效、系统的研究与应用平台，这也在一定程度上制约了疲劳可靠性技术与轻量化技术的进一步协同发展。

2012 年中车齐齐哈尔车辆有限公司建成了铁路货车车体疲劳试验台。铁路货车全尺寸车体疲劳试验台架建立并投入使用后，相继开展了C70E、C80敞车及BHP 矿石车车体疲劳试验，为提升和改进车体技术性能提供了技术支撑［4］。C70E敞车试验如图1 所示。

图1 铁路货车车体疲劳试验台

试验完成后，没有合适的仿真分析方法对试验过程中的现象进行解释。如何基于实物试验台架的相关参数建立合适的仿真分析方法是现阶段的研究重点。通过建立仿真方法可以缩短试验周期、降低试验成本，进行多方案的对比分析。仿真分析能够兼顾到全车应力分布，对实物试验测点的数量有效补充。

近年来，汽车行业采用将试验台架引入到仿真中，保证仿真与试验边界条件的一致性，使试验与仿真更具有对比性，已经证实试验边界条件在仿真分析中的关键作用。文献［5-7］建立的四自由度和六自由度轴耦合整车虚拟试验台架，将实物试验的迭代结果作为仿真模型的激励信号，分析结果被用来指导样机试验，甚至替代部分样机试验。与汽车行业全尺寸台架不同，全尺寸车体疲劳试验台是悬浮式试验台架，这是铁路货车全尺寸台架的特点也是仿真难点。

文中借鉴汽车行业的经验，对铁路货车全尺寸车体疲劳试验台架模型建模的关键技术进行研究。这种通过在仿真中引入全尺寸试验台架模型，同时基于实物台架修正模型的仿真模拟方法，使试验和仿真在真正意义上实现了相互指导和相互补充，也为复杂系统仿真提供有益探索。对提升铁路货车产品性能具有极为重要的意义。

1 虚拟车体台架的建模原理

车体疲劳试验台架由机械结构、电液伺服和电气控制等系统组成，如图2 所示。驱动输入信号通过控制系统控制油缸伺服阀达到指定的载荷，油缸将载荷传递给模拟摇枕，模拟摇枕再通过心盘、旁承和车钩将载荷传递给车体。若对系统载荷进行分析的话，仅需建立了机械结构系统模型，但此时机械系统的输入信号应该为作动器力、位移的反馈信号，该信号相比输入而言，反映了系统的真实输入。

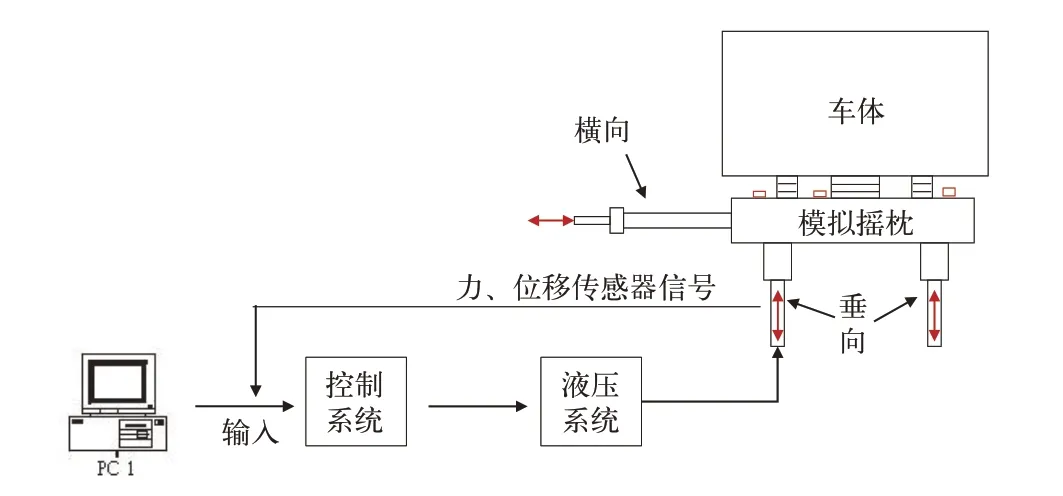
图2 试验系统简图

机械系统中由模拟摇枕、作动器组成的试验台架刚性较大，仿真模拟时将其考虑为刚体。采用Adams 进行多刚体建模，考虑约束方程，Adams利用到拉格朗日第一类方程的能量形式得到方程［8-9］为式（1）：

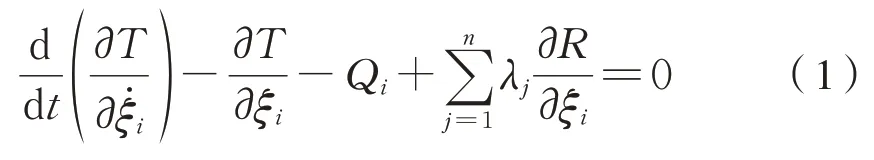
式中：ξ为反映刚体方位的广义坐标；T为广义坐标下动能；Qi为广义坐标下的方向力；λ为拉格朗日乘子；R为约束的表达。

设广义动量和约束反力分别为式（2）、式（3）：

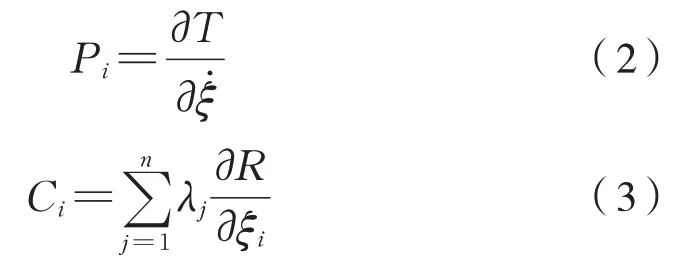
把式（2）、式（3）代入式（1），则能量方程可简化为式（4）：

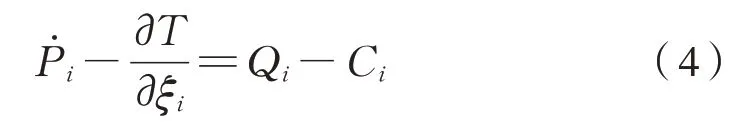
动能可以进一步表达为式（5）：

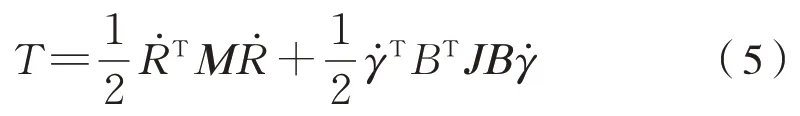
式中：M为构件的质量阵；J为构件在质心坐标系下的惯量阵；γ为广义坐标ξ中的转动坐标；B为广义坐标到构件质心坐标系的变换矩阵。

悬浮式试验台架构件的动力学参数选取直接影响仿真模拟精度，考虑到无法将构件拆分进行质量、质心及转动惯量测定，可建立较为细致的几何模型，通过几何模型获得上述参数，最后基于试验结果对参数进行简单修正即可。

刚性试验台架建立后，建立模拟摇枕上方心盘模型、旁承模型、车钩作动器的车钩模型，3 个模型均需要建立适用于试验台架模拟的工程模型。

在刚体的广义坐标中添加模态坐标mi后变成柔性体的广义坐标式（6）：

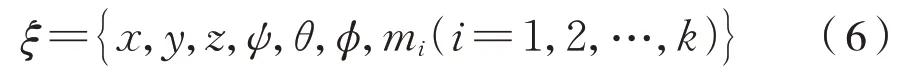
为了能获得较好的拟合静态、动态载荷条件下结构变形所需的模态集，我们将采用Craig-Bampton 模态综合法［10］来获取所需要的模态集Φ。故带柔性体的拉格朗日乘子的方程变为式（7）：

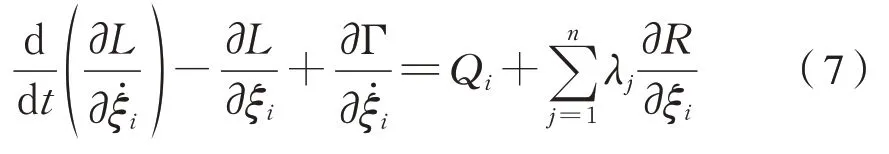
式中：L为T-W，动能与势能的差；Γ 为系统损耗函数。

对振动方程进行求解可获得弹性体广义模态坐标向量的时间历程，根据模态坐标，叠加模态应力以获得动应力的时间历程［11］。

需要将车体建成柔性体进行仿真应变和实测应变结果对比，完成台架校准。

2 台架仿真建模的关键技术

2.1 建模的流程

试验台仿真建模流程如图3 所示，具体为：

图3 建模流程

（1）利用Pro/e 软件建立较为细致的台架构件几何模型，将建立好的几何模型导入到Adams 软件中［12］，设置材料参数，计算构件的质量、质心及转动惯量。

（2）根据实物台架构件间的运动关系，添加约束（connectors）和驱动（motions）。

（3）在Ansys 软件中建立车体有限元模型。有限元模型的心盘、旁承和车钩部位采用刚性区建立与试验台架的连接点。分析台架上车体的频率分布，根据分析结果设置车体模态截取阶数。计算车体的质量归一化的模态中性文件，然后将模态文件导入到Adams 中，通过界面点与台架上的心盘、旁承及车钩模型进行装配。

（4）建立浮沉、侧滚和扭转等典型模态工况对台架模型进行校准，确定台架构件模型装配精度、约束的简化等参数的合理性。

（5）采用的线路随机信号驱动文件激励实物试验台，对台架的上车体振动加速度和应变进行测试。将实物试验台的载荷作为虚拟台架仿真模型输入，进行动力学计算；对比仿真与试验的车体加速度与应变结果，完成包含车体阻尼、车体模态阶数、心盘和车钩等参数的修正，最终实现模型的建立。

台架的载荷是自下而上进行传递的，文中也按这种方式对建模流程中涉及的关键技术进行研究。

2.2 台架模型的建立

试验台架由垂、横及车钩等作动器、模拟摇枕及其上面的心盘、旁承座等组成。

（1）作动器模型的建立

车体疲劳试验台架的所有作动器部件均由球铰和油缸2 种运动部件构成。以垂向作动器为例，如图4 所示，球铰可采用球铰副建立运动关系；油缸具有单向自由度，可采用滑移副建立约束关系，油缸内部为液压油，具有极好的润滑性，不必考虑滑移副的摩擦。横向作动器及车钩作动器的建模方法与垂向作动器相同。

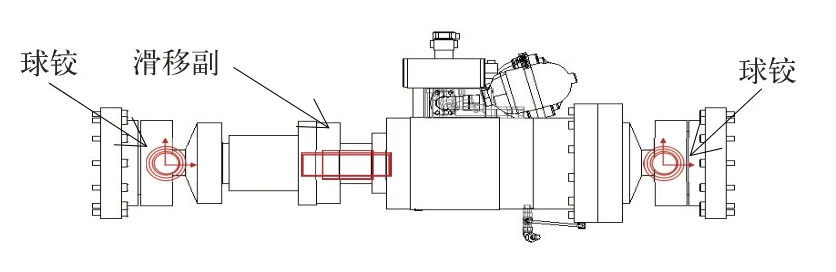
图4 垂向作动器仿真模型

（2）模拟摇枕建模

模拟摇枕上面的心盘和旁承用于连接车体，侧面和下部有连接座用于连接作动器，如图5 所示。模拟摇枕作为运动关系的核心构件，其上的连接件一定要保证位置精度，建议综合考虑图纸尺寸及实际测量结果进行建模。

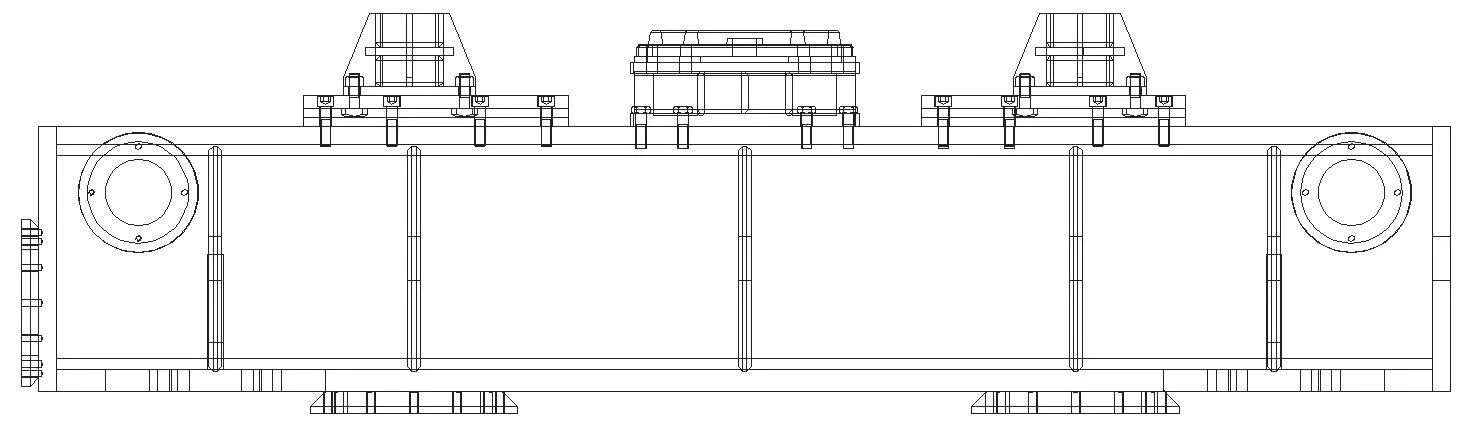
图5 模拟摇枕二维图

模拟摇枕上的旁承为常接触旁承，旁承为垂向刚度2 200 N/mm，纵向刚度为3 500 N/mm。重车状态下，旁承上表面距离滚子间隙为3～5 mm，故旁承刚度应为滚子间隙的函数，如图6 所示，装配零点到压缩4 mm 时，旁承刚度为2 200 N/mm，继续压缩时，由于滚子的接触，刚度变为极大，文中取值为400 000 N/mm。

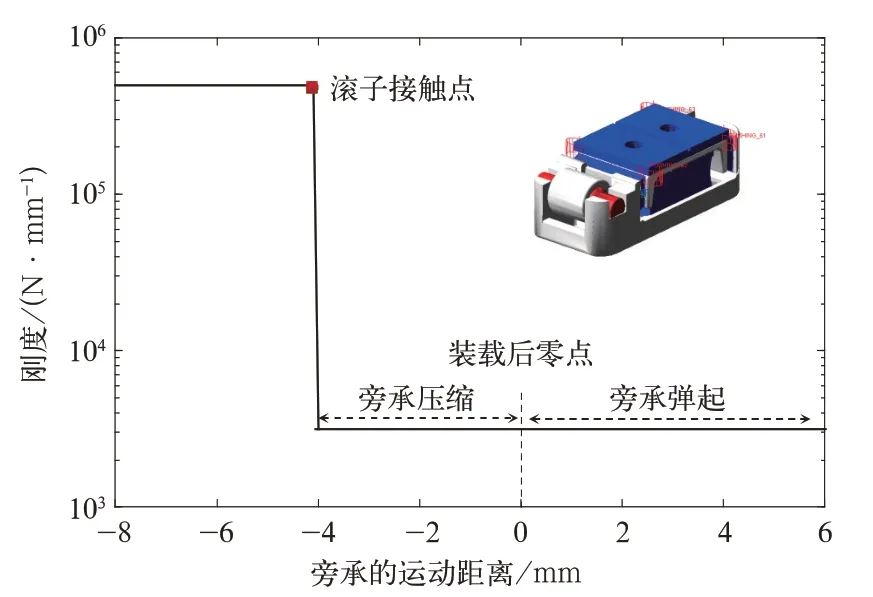
图6 旁承刚度曲线

台架无法模拟曲线运行状态，故摇枕上的心盘主要完成垂、横向载荷传递，不需要考虑回转阻力。在试验过程中考虑心盘发生脱离的影响，将心盘模型简化为4 点较大刚度的单边弹簧，弹簧刚度将在系统模型搭建完成后进行讨论，如图7所示。

图7 心盘刚度曲线

（3）纵向车钩作动器建模

台架为了能够实现纵向载荷传递，取消了车钩缓冲器，换成了刚性单元（假车钩），如图8 所示。该假车钩在拉伸载荷时作用在车体前丛板，压缩载荷时作用在车体后丛板。为了实现该功能，在前后丛板处分别建立2 个力元，中部建立1 个滑移副。力元函数仅具有压缩刚度，拉伸刚度为0，这样能保证只有一侧丛板受力。以前丛板受力时为例，力元1 压缩，前丛板受压，而力元2 拉伸，由于拉伸刚度为0，故后丛板不受载荷作用。

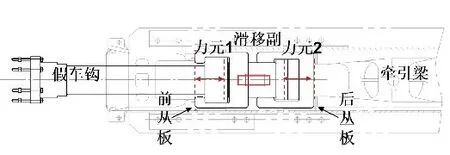
图8 车钩力元的刚度曲线

（4）台架模型总成

不考虑非载荷传递部件，总成后的台架模型包含189 个部件，其 中：2 个圆柱副，32 个 球 铰，10个滑移副，8 个点线约束和12 个位移驱动，如图9所示。

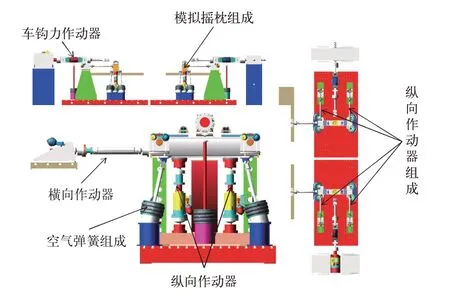
图9 试验台架仿真模型

2.3 柔性车体建模

文中选用的车体模型为C70E敞车，对于这种装载散粒货物的敞车而言，如何处理散体与敞车车体的关系是柔性体建模的关键。文献［13］认为散体材料的受压屈服强度远大于受拉屈服强度，且受剪时颗粒会膨胀，常用的VonMises 屈服准则已不适用，采用Ansys 的D-P 模型能够更加准确地模拟散体的变形与受力状态。计算结果表明，刚体和弹性体的模态顺序一致，一阶垂向弯曲和一阶横向弯曲结果相符，但由于散体不能反映运动滞后的特点，侧滚和扭转频率具有一定的误差。文献［14］利用试验台对C70E敞车进行了不同边界及不同散货装载条件下的模态试验，结果表明，散粒的实、松状态对车体刚体和弹性体频率影响很小，散粒货物主要影响车体的侧滚振型和侧墙的振动。

一方面考虑到车体底架的焊缝结构疲劳寿命决定车体疲劳寿命，而侧墙对车体使用寿命影响较小［15］。另一方面，对于敞车而言，侧滚等刚体模态对车体应力贡献较小，弹性体频率对应力贡献较大。鉴于此，为简化模型，将散体简化为质量单元附加到底架地板单元上。柔性车体的阻尼比值采用C70E敞车模态试验结果，超出试验频率的部分按5%设定。

将柔性车体与刚性台架模型装配后，开展装配体模态分析，装配体模态振型结果如图10所示。

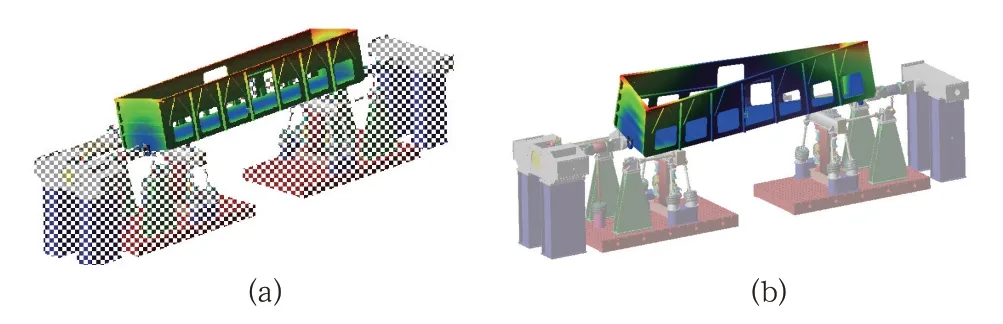
图1 0 系统装配模态

仿真与试验的模态结果对比见表1，由于没有转向架，该系统主要为侧滚、扭转频率和垂向一阶弯曲频率，侧滚频率误差为10.2%，扭转频率的误差为36.8%，垂向一阶弯曲频率误差为1.44%。频率的差异一方面与散粒简化到地板上有关，另一方面与散货—敞车的耦合有关。

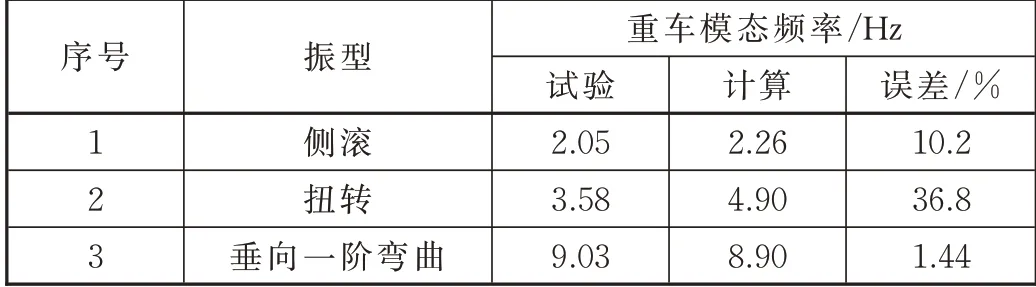
表1 仿真与试验模态频率结果对比

系统模型建立后，开展心盘衬套的刚度参数对系统模态的影响研究，不同刚度值下的系统模态结果见表2，心盘衬套刚度主要影响侧滚频率，当刚度从30 000 N/mm 变到60 000 N/mm 时，侧滚频率由1.91 Hz 变到2.26 Hz，变化幅度较小，可见，实际建模时，心盘刚度根据车体载重选取即可，对于C70E敞车，将车体和货物载重取为80 t，弹簧刚度为50 000 N/mm。

表2 仿真与试验模态频率结果对比

3 实例验证

3.1 典型工况的验证

采用5 sint的正弦信号建立浮沉、侧滚和扭转工况，激励虚拟试验台，在摇枕上和车体枕梁上建立2 个虚拟位移传感器，分别为DZB11 和DZN11，如图11 所示。

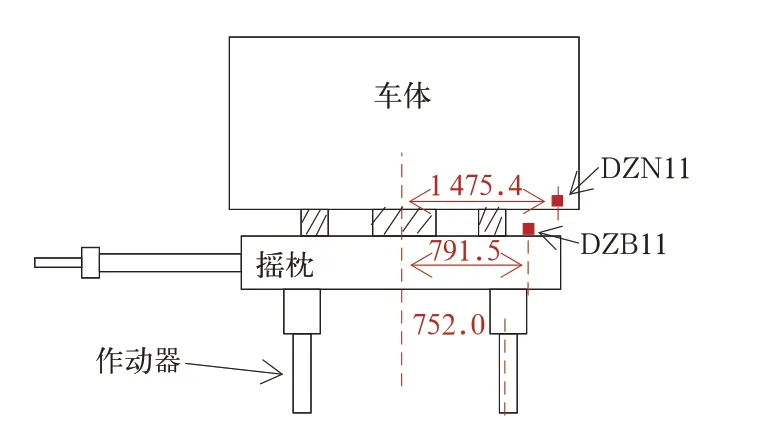
图1 1 试验台架简图

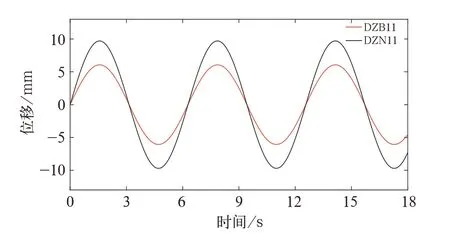
图1 2 侧滚工况下虚拟位移传感器计算结果

3 个工况的模拟结果均较好，以侧滚工况为例，仿真计算结果如图12 所示，测点DZB11 的位移为6.062 3 mm，测点DZN11 的位移为9.706 mm。根据作动器位置及测点位置的几何关系，作动器产生5 mm 位移，模拟摇枕测点位置的理论位移值为6.08 mm，车体枕梁部位的理论值为9.6 mm，可见仿真结果与理论计算结果一致。

3.2 线路随机载荷工况的验证

由于试验台是自下而上激励的悬浮式试验台架，若作动器全部采用位移控制模式时，由于系统的强耦合特性，仿真结果不易收敛。对于铁路货车车体无约束的仿真模式，仿真采用力控制和位移控制的组合是比较恰当的，即垂、横向作动器为位移控制，车钩力为力控制。

选取试验台迭代好的线路随机工况驱动文件，将该文件同时施加到仿真模型上和实物试验台架上，对比车体加速度和应力结果。其中车体1位端1 侧垂向加速度AZN11 结果的时域波形如图13 所示，仿真与试验的波形基本一致。

对枕梁加速度进行PSD 分析，如图14 所示，由PSD 分析结果对比可见，6 Hz 以内频率一致，6 Hz以上曲线形状一致，但幅值上稍有差异。

车体枕梁部位6 个加速度RMS 对比分析，结果如图15 所示，垂向振动加速度RMS 误差低于22%，横向加速度的RMS 误差最大值比垂向的误差大，误差最大为31%，横向误差较大可能与散体货物重心的降低有关。

进一步考虑车体实测应变与仿真结果的差异，车体大横梁端部横向测点SH1 的试验与仿真结果如图16 所示，波形的一致性较高。车体中梁中部纵向应变测点SZ02，波形一致性较好，如图17所示。

图1 7 中梁中部纵向应变测点结果对比

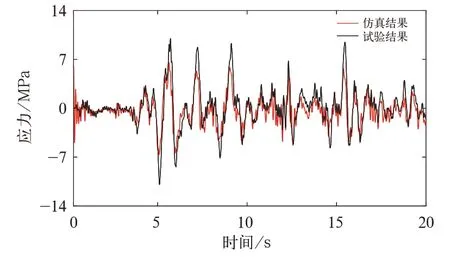
图1 6 大横梁端部横向应变测点结果对比

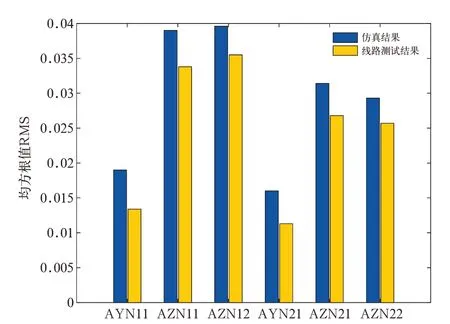
图1 5 枕梁加速度的统计结果对比

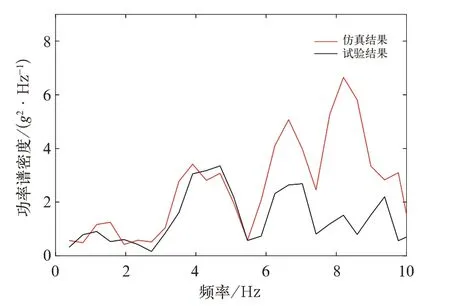
图1 4 车体枕梁1 位端1 侧垂向加速度PSD 结果对比

图1 3 车体枕梁1 位端1 侧垂向加速度结果对比

综上所述，建立的虚拟车体试验系统，能够将试验的驱动施加在仿真模型上，保证计算后的车体加速度与车体动应力结果基本一致，该虚拟系统将为后期开展虚拟试验方法研究提供基础模型。

4 结 论

（1）基于刚柔耦合多体动力学理论，依托铁路货车全尺寸车体疲劳试验台架，完成了台架作动器、心盘、旁承、车钩、柔性车体等关键技术建模，最终建立了刚柔耦合多体虚拟试验系统模型。

（2）通过侧滚和浮沉等典型工况、试验多个作动器驱动文件进行了虚拟试验台架的车体动态响应计算，结果表明：车体枕梁加速度和关键部位动应力仿真结果与试验测试结果波形一致，验证了试验台架建立方法的合理性。

（3）虚拟试验台架解决了全尺寸车体疲劳试验周期长、成本高的问题，为开展铁路货车领域的虚拟台架试验提供了有力依据。同时该模型能够为后期虚拟车体疲劳评估提供基础数据，使试验和仿真相互补充、相互指导。