基于虚拟样本生成的铈镨/钕组分含量预测*

陆荣秀， 赖路璐， 杨 辉， 朱建勇

(1.华东交通大学 电气与自动化工程学院，江西 南昌 330013；2.江西省先进控制与优化重点实验室，江西 南昌 330013)

0 引 言

从共生矿中分离得到的稀土产品是极其重要的战略资源。快速获得萃取槽体中元素组分含量分布，是实现稀土萃取分离过程各关键工艺参数实时调节的关键环节[1]。目前，绝大多数稀土分离企业采取“定时采样、离线实验室化验”的方式获取组分含量[2],不能满足生产现场实时性要求。近几年，很多稀土研究工作者将数学建模中数据驱动建模思想应用于稀土萃取过程的组分含量检测，如文献[2,3]以HSI颜色空间的H,S,I分量为输入，建立基于最小二乘支持向量机(least square support vector machine,LSSVM)的组分含量预测模型，实现稀土元素组分含量的快速测量。

鉴于稀土萃取过程数据获取成本高、数据重复等原因，造成有效过程数据不多，易导致模型预测精度不高、泛化性能不佳[4]等小样本问题[5,6]，借鉴矿冶化工过程[7]、石油化工过程[8]等领域研究小样本问题的成功案例，通过合理方法扩充样本数量，利用大数据技术背景下的智能建模方法提高稀土萃取过程模型的预测精度是一条有效途径。

本文以CePr/Nd萃取过程为研究对象，利用随机配置网络(stochastic configuration network,SCN)方法具有收敛速度快、泛化能力较强的优势[9]，在建立CePr/Nd溶液图像颜色特征与Nd组分含量关系模型的基础上，采用线性中点插值的方式生成虚拟样本，提出一种基于虚拟样本构造的CePr/Nd取过程组分含量预测方法。通过CePr/Nd萃取生产现场的数据进行实验验证，结果表明该方法以扩增虚拟样本数据集的方式，为基于数据驱动的预测模型提供有效数据，可提高组分含量预测模型的精确性和泛化能力。

1 CePr/Nd萃取过程描述及溶液特性分析

1.1 稀土萃取工艺流程

图1以CePr/Nd混合料液为例，描述了稀土分离企业的溶剂串级萃取流程工艺。

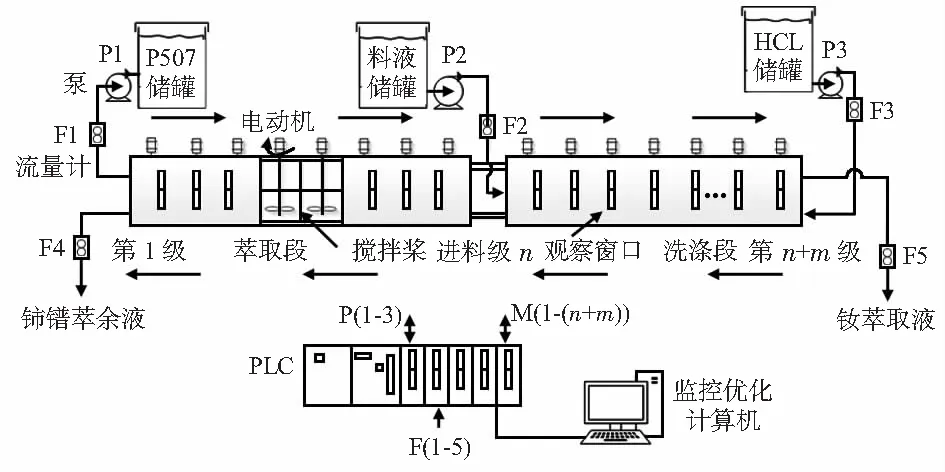
图1 CePr/Nd萃取生产流程

图1中待分离料液中包括的稀土元素为Ce,Pr和Nd，根据元素与萃取剂、洗涤剂的络合度以及生产线的设定要求，Nd为易萃组分，即洗涤段出口为富含Nd离子的萃取液，相应地，Ce,Pr为难萃组分，萃取段出口则为富含Ce,Pr离子的萃余液。由于各元素之间物理化学性质相近、影响萃取分离效果的因素多样，萃取分离过程的每一级均要经过搅拌、澄清，整个萃取流程存在级数多、耗时长、强耦合、非线性等特点[10]，在萃取段和洗涤段各设置一个监测点，通过检测监测级萃取槽体中各元素组分含量，并据此调整萃取过程各关键工艺参数。

1.2 CePr/Nd混合溶液特性分析

由于稀土元素具有独特的电子结构，在图1所示的P507-HCL萃取体系中， Pr、Nd可呈现不同的离子颜色特征，即Pr、Nd离子分别富集在萃取段、洗涤段并逐渐显现出苹果绿和紫红色，其他各级萃取槽体均因Pr、Nd和无色的Ce元素组分含量不同而显现出不同混合溶液颜色[11]。据此，可利用机器视觉技术采集稀土混合溶液图像，采用智能建模方法描述溶液图像颜色特征与组分含量之间的函数关系。鉴于HSI颜色模型可以直观反映人的视觉系统感知彩色的方式，本文使用HSI颜色空间下颜色分量一阶矩描述稀土混合溶液的图像特征[12]，表达式如式(1)

(1)

式中μ为图像ic(x,y)中颜色特征分量的一阶矩，ic(x,y)为图片颜色特征分量矩阵元素值，其中，P,Q分别为颜色特征分量矩阵行元素个数和矩阵列元素个数，在此，P=Q=128。图2为CePr/Nd萃取槽体混合溶液图像特征分量H，S,I的一阶矩与Nd元素组分含量之间的关系曲线。

图2 H,S,I分量一阶矩与Nd组分含量的关系

由图2可知，根据稀土混合溶液图像H,S,I分量的一阶矩可确定溶液中Nd组分含量，用式(2)表示稀土混合溶液图像颜色特征分量一阶矩与组分含量之间的非线性函数关系

y=f(xH,xS,xI)

(2)

式中y为Nd组分含量，xH,xS,xl分别为颜色空间的H，S，I分量一阶矩。

描述式(2)所示的非线性函数的方法有多种，如神经网络、深度学习等，但这些方法均要求历史数据的完备性，而稀土萃取过程具有典型的小样本特点，要得到预测精度较高和泛化能力较强的组分含量预测模型，需采用虚拟样本生成方法以补充生产现场数据的不足。

2 基于SCN的虚拟样本生成

虚拟样本生成的基本思想是依据较少的真实样本数据，通过某种变换产生新的、符合研究对象生产过程规律的样本，其目的是通过信息间隔填充，弥补真实样本数据不足致使模型精度不高、泛化能力不强等问题[13～15]。实现虚拟样本生成方法有多种，最常用的方法为插值法[4]，基本思路是根据生产过程特性产生虚拟输出样本，再根据样本间的特征信息和转换关系得到虚拟输入样本，从而构成虚拟样本集[16]。

针对稀土萃取过程的真实小样本数据，通过SCN方法建立Nd组分含量和H，S，I分量一阶矩的非线性关系，然后从小样本数据补充角度分析，采用插值法对萃取过程缺失的、稀疏的数据进行增补。如图3所示为基于SCN的虚拟样本生成原理。

由图3可知，采用SCN生成虚拟样本的基本思路是：在依据原始真实小样本数据建立SCN模型的基础上，根据SCN模型隐含层和输出层之间呈线性关系，采用基于中点插值方法得到虚拟样本的输出数据值，在此基础上，由输入层与隐含层的非线性映射得到虚拟样本的输入数据值，最后将得到输入、输出数据值构成虚拟样本集。

图3 基于SCN的虚拟样本生成原理

2.1 SCN模型结构

相较于传统梯度类算法，随机算法因其具有快速性、不易陷入局部极小而常用于神经网络学习。文献[9]提出一种新型随机权神经网络，即随机配置网络。

SCN模型是一个由输入层、隐含层、输出层组成的3层前向反馈网络结构。结合式(2)，给定目标函数f︰Y∈RN×1→X={xH,xS,xI}∈RN×3，其中N为样本数。假设SCN模型此时已有L—1个隐含层节点，即

(3)

当模型输出的残差eL-1不满足式(4)，则增加新的隐含层节点，即新模型共有L个隐含层节点，模型输出如式(5)

|eL-1|=|Y-YL-1|

=|[eL-1,1eL-1,2,…,eL-1,m]|<ε

(4)

式中ε>0为系统的容忍误差。式(5)如下

(5)

式中 新增节点的输出权值βL表示为

(6)

若隐含层的输出权值为β=[β1,β2,…,βL]，式(5)则可以写成式(7)

YL=H·βL

(7)

在上述推导过程中可知：SCN算法最大的特点是隐含层节点的可变性，需要设置的参数为最大节点数量L和可容忍误差ε，直到满足任意一个停止条件时，网络停止训练并输出最终模型[17]，隐含层节点的可变性使得随机配置网络更具有灵活性。

2.2 基于SCN的虚拟样本生成方法

2.2.1 插值原理

为了尽可能地简化计算，本文采用欧氏距离相似度在隐含层输出中点线性插值方法，首先，确定插值位置的起始行xHq,xSq,xIq(q=1,2,…,N)，然后，按式(8)计算起始行与隐含层矩阵各行间基于输入变量的欧氏距离dq(q=1,2,…,r)，基于式(9)选取最优欧氏距离d作为插值的终点xHq+1,xSq+1,xIq+1。式(8)、式(9)如下

(8)

d=min{dq}，q=1,2,…,r

(9)

插值过程如图4所示，利用SCN网络的映射关系，在SCN隐含层输出矩阵中进行线性中点插值，得到虚拟输出，最后，反推求得一一对应的虚拟输入。

图4 隐含层输出在第i行和第j行线性中插过程

2.2.2 虚拟样生成方法

基于采集到的少量真实小样本数据，依据式(2)，采用SCN方法建立H,S,I一阶矩分量与Nd组分含量的SCN模型。

由2.1节可知， SCN模型有3个输入节点，若真实样本的训练集Qt={Xt,Yt}(t=1,2,…,tn)，t为真实样本个数，则隐含层输出矩阵H为

(10)

式中Hhij为H矩阵里第i行第j列元素。

根据2.1节，通过训练集Qt建立SCN模型，可得到隐含层输出矩阵与模型输出的一一对应关系

(11)

假设隐含层输出矩阵的第一行为插值起始行，利用SCN模型隐含层和输出层之间呈线性关系的特点，采用中点插值法求取虚拟样本的输出值，即

(12)

式中Y′为虚拟样本的输出。

假设与第一行(即起始行)最优欧氏距离是隐含层输出矩阵的第二行，即

根据2.2.1节，采用线性中点插值后隐含层输出的结果是

(13)

N次中插后，由式(11)得到隐含层与网络输出的对应关系为

(14)

根据输入层与隐含层之间的非线性映射关系进行反推，得到SCN的输入数据X′

X′=(wl)†(φ-1(H′)-bl)

(15)

式中 (wl)†为输入权值矩阵的广义逆，φ-1(·)为激活函数的逆，即

(16)

如果输入权值矩阵wl是一个可逆平方阵，输入权值矩阵可由矩阵的逆计算得到(wl)-1，反之，依据广义逆矩阵的唯一存在性，输入权值的广义逆(wl)†可由下面式子计算得到

(wl)†=((wl)Twl)-1(wl)T

(17)

综上所述，经过Nv次隐含层输出线性中点插值后可得到如式(18)的N个虚拟样本

(18)

至此，虚拟样本生成过程结束，虚拟样本生成的具体流程如图5所示。

图5 虚拟样本生成流程

3 实验验证与分析

为了验证本文所述方法的有效性，依托江西某稀土公司的CePr/Nd取生产线，不同时刻不同工况条件下在萃取段和洗涤段的监测级萃取槽体中获得65份样本溶液，将混合溶液做好标记并分成两部分，一部分采用离线实验室检测方法得到Nd组分含量，另一部分用于混合溶液图像采集，并提取溶液图像的H,S,I颜色特征分量，将颜色特征分量一阶矩与Nd组分含量组成历史样本数据集。为了测试训练模型的有效性，随机抽取50组原始样本作为训练样本，表示为：Ttr={Xtr,Ytr}={xHtr,xStr,xItr,ytr}∈R50×4，剩余15组原始样本为测试样本，表示为：Tte={Xte,Yte}={xHte,xSte,xIte,yte}∈R15×4。衡量模型性能的指标采用：相对误差绝对值的最大值(MRE)，均方根误差(RMSE)，表达式如下

(19)

(20)

为了体现本文方法的优越性，设计了两个实验：

实验一根据第2节的基于SCN的虚拟样本生成方法，依次增加10个虚拟样本，实验7次，然后采用测试集Tte对各模型进行测试。各个组分含量SCN模型的各项性能值如表1所示，每一个模型的相对误差变化如图6所示。

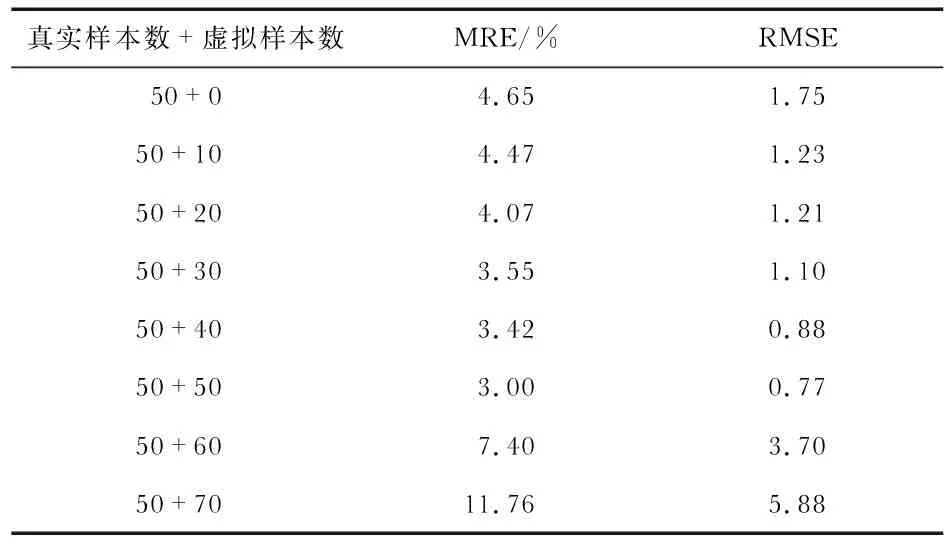
表1 不同虚拟样本的SCN模型性能

图6 不同虚拟样本SCN模型的相对误差

分析表1和图8可知,1)当虚拟样本数量分别从0增加50的过程中，预测模型的MRE和RMSE值在不断降低，即采用了虚拟样本生成技术的组分含量模型比未采用该技术的模型性能高，且随着虚拟样本数的增加，模型性能不断提高；2)当虚拟样本数量大于训练样本数量时，模型的测试性能不升反降，说明当扩增样本数量等于训练样本数量时，组分含量SCN模型预测性能最优。

实验二1)使用和实验一相同的训练集和测试集，分别采用SCN、SVM、LSSVM、WLSSVM方法建立组分含量模型，得到虚拟样本生成前各模型的性能指标；2)以实验一中最佳虚拟样本数(即50)为基准，将原有的65个真实样本数据和50个虚拟样本数据混合，随机选择86组数据作为训练样本，剩下29组数据作为测试样本，分别采用SCN、SVM、LSSVM、WLSSVM方法进行建模，对比模型测试的性能指标。数据扩增前后，SCN的停止训练的参数均设置为可容忍误差ε=0.001，最大隐含层节点数L=50，其他各模型参数设置如表2所示。SVM、LSSVM方法均使用交叉验证的方式确定最佳惩罚参数c,核函数参数g,正则化参数γ和核函数σ；WLSSVM方法的输入权重wH,wS,wI采用互信息加权方式确定,各输入变量和输出变量之间的互信息为mH,mS,mI；γ和σ采用交叉验证法确定。得到的各模型性能指标值如表3所示。

表2 数据扩增前后的各模型参数

表3 数据扩增前后各模型的测试性能指标

分析表3可知，1)虚拟样本生成前，组分含量SCN模型的性能比基于SVM、LSSVM和WLSSVM的组分含量模型性能更优；2)当生成50个虚拟样本后，各组分含量模型的性能指标值与虚拟样本生成前相比较均减小了很多，说明采用基于SCN中点插值生成的虚拟样本，同样适用于SVM、LSSVM、WLSSVM等方法建模。

综上分析，采用SCN方法生成虚拟样本，实现CePr/Nd萃取过程组分含量预测的途径是可行的，实验的结果表明，该方法可以满足稀土萃取生产现场元素组分含量的准确预测。

4 结束语

本文针对稀土萃取生产现场采集数据难，可获得的真实样本数据少，建立组分含量模型时易出现小样本问题，提出基于随机配置网络进行虚拟样本生成的组分含量预测，该方法充分考虑了输入和输出数据的非线性特性，可以有效缓解稀土萃取过程历史样本数据不完备的缺陷。以CePr/Nd萃取生产现场数据测试为依托，通过虚拟样本生成前后的组分含量模型测试性能对比，及将生成的虚拟样本数据用于SVM、LSSVM、WLSSVM建模的实验分析，结果表明：基于SCN进行虚拟样本生成的组分含量模型具有较高的预测精度，生成的虚拟样本数据也适用于其他建模方法，可为提高具有小样本特点的稀土萃取过程组分含量模型预测性能提供新的思路，同时，也可为其他具有小样本特点的复杂工业过程建模提供参考。