基于压电振动能量采集器的信息感知与模式识别系统*

颜佟佟， 鲁征浩， 徐大诚

(苏州大学 微纳传感技术研究中心，江苏 苏州 215006)

0 引 言

环境振动状态的识别对于现场感知、侦查和信息研判显得尤为重要。例如，在石油管线、公路围栏和要地目标的监控中，快速识别出监测目标的振动类型(对石油管线、围栏等的敲击破坏)对于安全运行具有重要的意义。目前，大多数振动模式识别系统都采用加速度计作为检测传感器[1,2]，但加速度计需要电源才能获得相关数据，压电能量采集器实现了振动能转换为电能的自供电，并能获取环境振动信息，如果能对信息识别出环境振动模式，便可以达到无源自感知和智能识别的目的。

Khalifa S等人[3]从压电能量采集器输出电压中提取均值和标准差特征，再通过机器学习K近邻法识别出了行人站立、行走、跑步等运动状态。Ma D等人[4]从压电能量采集器电压信号中提取平均值、标准差等22个特征，采用支持向量机等算法识别步态引起的振动模式。Hassan M等人[5]从压电能量采集器输出的交流电压中提取最大值、频域最高幅值与所有幅值之和的比值等特征，采用决策树分类器识别热词引起的振动类型。由此可见，目前基于压电能量采集器的信息感知主要应用于行走等人类运动状态识别，且多采用传统的机器学习方法。对于许多重要目标如石油管线、防护围栏等安全监测，特别是识别具有破坏行为(如人为摇晃、重物敲击)的振动类型意义重大，而此类振动模式的识别鲜有文献报道。

本文提出了一种环境振动状态识别方法。通过压电能量采集器获取振动状态信息，利用卷积神经网络(convolutional neural network,CNN)算法处理压电能量采集器输出电压信号，实现在能量采集器发电的同时，识别出敲击或摇晃等振动模式。同时，设计了基于FPGA的验证系统，通过算法运行完成实时识别的功能验证。

1 振动阈值触发压电能量采集器

振动阈值触发压电能量采集器结构如图1(a)，(b)所示。该能量采集器采用两级振子结构，其中，外框耦合环境振动状态，通过磁能耦合激励内框发电谐振子产生谐振，进而产生电能和感知信息。当振动强度小于磁能耦合阈值时，两级之间无法克服磁排斥力，只能在平衡位置小幅振动；当振动强度大于阈值时，磁能耦合克服磁屏障力，进而触发发电振子谐振发电。

图1 振动阈值触发压电能量采集器结构

在振动阈值触发压电能量采集器发电的同时，其输出信号可以用于振动状态识别。当振动强度低于阈值时，认为没有振动事件发生；当振动强度高于阈值时，采集器触发且不同振动模式(敲击、摇晃)下输出电压模式不同，因此可以通过电压信号识别不同的振动模式。

2 基于CNN的振动模式识别

2.1 CNN

传统机器学习方法需要人为提取特征，深度学习是一种端到端的方法，无需额外的特征提取过程，通过网络自身学习分类任务中最具判别力的有用特征[6]。CNN是深度学习算法中的基本结构之一，一般包含卷积层、池化层和全连接层。

1)卷积层

卷积层利用多个卷积核对输入数据进行卷积处理提取特征，输入输出均称为特征图。相比于全连接层，卷积层具有网络局部连接和卷积核参数共享的特点，能够在参数较少的情况下提取特征。卷积层可以定义为

ai=f(ai-1*Wi+bi)

(1)

式中ai-1为第i层的输入特征图，ai为第i层的输出，Wi为第i层的卷积核，bi为卷积核的偏置，*为卷积操作，f为激活函数，通常选取ReLU函数，进行非线性变换。其运算式为

f(x)=max(0,x)

(2)

2)池化层

池化层作用是对输入特征图进行降采样，在实现数据降维的同时进一步提取主要特征信息。常用池化操作为最大池化和平均池化。池化层可以定义为

ai=g(down(ai-1))

(3)

式中down为下采样函数，g为池化函数。

3)全连接层

池化层得到的特征图需要转换成1维向量，再输入全连接层实现分类。全连接层可以定义为

ai=σ(Wiai-1+bi)

(4)

式中Wi和bi分别为第i层的权重和偏置，σ为激活函数。

2.2 数据获取与样本构造

为了获取训练数据，将能量采集器放置在激振器(JZK—10)上，利用激振器模拟摇晃和敲击两种振动模式，其中,摇晃理想化为正弦振动，敲击近似为半正弦脉冲振动，通过存储记录仪(MR8880—21)记录能量采集器的输出电压，采样率为1 kHz。在不同频率(1～7 Hz)和不同振动强度(2～6.5 g)下分别获取摇晃和敲击两种振动模式下能量采集器的输出，记录为两个长时间序列。由于能量采集器自身具有阈值触发特点，因此当能量采集器触发时，再判断振动模式。能量采集器未触发时，输出电压不会超过0.5 V。因此对于采集到的两个长时间序列，分别从第一个数据开始遍历，当该点电压大于0.5 V时，以该点为起点取连续的500个数据作为一个样本并打上标签(摇晃为0,敲击为1)，如图2所示。最终获得7 000个样本，包含3 500个摇晃样本和3 500个敲击样本。

图2 样本构造示意

2.3 CNN模型构建

Lecun Y等人[7]指出一维CNN适用于序列数据，二维CNN适用于图像数据，三维CNN适用于视频数据。能量采集器输出电压信号为一维数据，因此卷积核采用一维结构。在传统CNN结构的基础上针对参数量和计算量做改进，降低模型对FPGA硬件实现的资源需求。由于能量采集器输出电压数据变化较为缓慢，因此,模型的第一层为最大池化层S1，池化窗口宽度为5，在提取特征的同时减少后续运算量。第二层和第三层分别为卷积层C1，C2，用来提取特征。借鉴轻量化网络模型SqueezeNet[8]中用1×1卷积核代替3×3卷积核的思路，并结合一维卷积特点，卷积层C2滤波器长度设为1，有效降低了参数量。第四层为全局最大池化层S2，降低进入全连接层的数据维度。第五层全连接层实现最终的分类，为了防止过拟合全局最大池化层后使用Dropout[9]方法。最终模型结构如图3所示。

图3 CNN模型结构

2.4 模型训练结果

构建的CNN模型进行算法验证的软件环境为：Python语言和Tensorflow深度学习框架。模型的目标函数为交叉熵损失函数，优化算法为Adam[10]。模型的评价指标为准确率，即模型正确分类的样本个数占总个数的比例。对于7 000个样本数据，通过分层抽样取出4 900个样本用于训练，2 100个样本用于测试。神经网络的参数一般根据人为经验设定，往往难以确定。通过不同超参数模型的测试准确率对比，寻找模型的相对最优结果。表1所示为模型在不同超参数下的测试准确率，综合对比后选取实验3作为CNN的超参数配置。

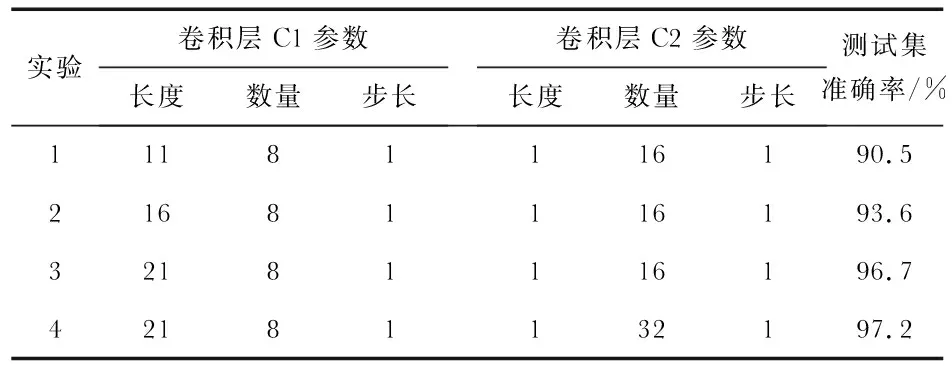
表1 不同超参数下测试集准确率

2.5 算法比较

将构建的CNN模型与机器学习算法逻辑回归(logistic regression,LR)、K最近邻(K-nearest neighbor,KNN)法、支持向量机(support vector machine,SVM)进行对比。传统机器学习算法需要人为提取特征，本文从时域和频域共提取8个常用特征，时域特征为最大值、最小值、均值、标准差、均方根；频域特征为幅度谱最大值、0～100 Hz频段幅值的和、400～500 Hz频段幅值的和。表2所示为几种算法识别准确率对比，在人为提取的特征下KNN法和SVM准确率均达到了89 %左右，相比之下CNN模型识别准确率最高，达到96.7 %。

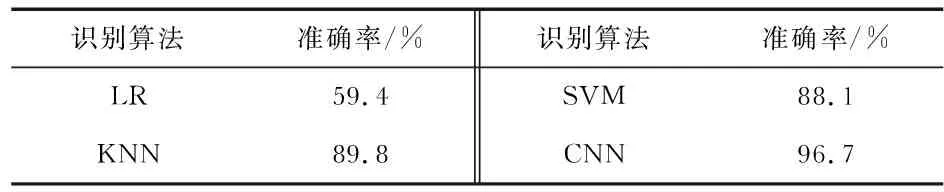
表2 不同算法准确率

3 识别系统测试

3.1 测试方案

通过FPGA搭建了振动模式实时识别系统，系统框图如图4所示。其中FPGA芯片为Zynq 7020，AD芯片为AD7606。系统工作时首先通过FPGA控制AD以1 kHz采样率采集一个数，如果该数大于0.5，则AD连续采集500个数据送入FPGA运行CNN算法输出识别结果；否则AD继续采集下一个数。系统测试现场如图5所示。

图4 识别系统框图

图5 系统测试现场

3.2 测试结果

通过激振器模拟5 Hz敲击和摇晃，图6所示为FPGA的输出。当没有振动事件发生时，输出电压接近0 V，FPGA输出识别结果00；当发生敲击事件时，能量采集器触发且输出电压经分压后峰值达到2 V左右，FPGA在0.6 s内输出01；当发生摇晃事件时，输出电压经分压后峰值同样达到2 V左右，FPGA在0.6 s内输出10。对1～7 Hz的敲击和摇晃分别进行多次测试，在35次摇晃测试中FPGA全部识别成功，在35次敲击测试中FPGA识别错误3次，测试准确率达到95.7 %。

图6 识别结果

4 结 论

基于振动阈值触发压电能量采集器，采用CNN算法，通过FPGA验证系统，实现了摇晃和敲击两种振动模式的识别，实际测试准确率可达96.7 %。实验结果验证了识别方法的有效性和正确性，使得压电能量采集器在发电的同时实现了信息感知以及状态识别的智能自感知目的。