基于人眼亮度感知的S 型函数图像对比度增强算法

王一竹，李 渊，杨 宇

(1. 无锡职业技术学院控制技术学院 江苏 无锡 214121；2. 国网青海省电力公司检修公司 西宁 810001；3. 东南大学仪器科学与工程学院 南京 210096)

如果设备性能较差，或照明条件不理想，数字图像的对比度往往很低。低对比度的图像看起来非常模糊，不能充分展示图像的细节，因此研究人员提出了各种算法来提升这些图像的视觉效果。

对比度增强技术大致可分为直接增强和间接增强两类。文献[1]是比较典型的直接增强算法，通过应用各种非线性函数[2]或求解优化问题[3]来改进图像对比度。这些增强效果是通过人眼视觉系统(human visual system, HVS)来 衡 量，如Weber-Fechner 定律或Retinex理论[4]等。此方法在图像细节增强和动态范围压缩方面有一些优势，但计算复杂度较高，并导致了“晕”伪影，特别是在强边缘[5]周围，“晕”伪影尤其明显。尽管近几年提出的直接方法，缓解了这些问题，但仍然缺少能够兼顾高图像对比度和实时计算效率的算法。因此，基于全局变换函数的间接方法有着更为广泛的应用。

在间接方法方面，直方图均衡化(histogram equalization, HE)是最具代表性的方法之一。当图像直方图中出现高峰值时，会产生视觉伪影，如噪声放大、轮廓化或显著的亮度变化等。为了缓解这些问题，基于HE 的方法对图像直方图进行修改，使其峰值衰减，然后由修改后的直方图得到变换函数。如文献[6]通过求解双准则优化问题，将图像直方图与均匀分布相结合；文献[7]使用归一化幂律函数，平滑图像直方图中的峰值。由于间接方法能够将增强后图像的平均亮度转移到中等灰度级别，因此将图像直方图分割成多个子直方图，并对每个子直方图分别进行HE 处理[8]。为了保留细节，文献[9]提出了利用二维(2D)直方图均衡化的间接方法，模糊上下文信息来构建图像直方图，赋予纹理区域的像素更高的权重。与其他间接方法相比，此方法具有更好的对比度增强性能和更少的信息损失。

以上这些方法在低照度的情况下，对图像的处理能力较差，难以达到理想的效果。这主要是因为在低照度情况下，人眼对图像处理的方式与正常照度下的模式不同。为此，本文首先引入了一种新的基于人类亮度感知的评价对比敏感度的S 型函数。由于人类视网膜的对比敏感度随着亮度(取对数)的增加呈指数级下降，因此将对比敏感度建模为对数参数的指数函数。利用对比灵敏度模型，通过修改Steven 幂律的指数，导出S 型函数。此外，本文还提出了一种参数优化方法，在保持输入图像的平均亮度和扩展图像的直方图的同时使信息损失最小化。

1 人类视觉特点分析

1.1 人类感知亮度

人类视网膜上的光感受器包括视杆细胞和视锥细胞两种。视杆细胞对光线很敏感，在低亮度水平下能够提供消色差视觉，这种视觉也称为暗视觉(10−6～10 cd/m2)。在亮度水平高于10−2cd/m2时，视杆细胞开始饱和，视锥细胞提供名为明视觉的色觉。在亮度水平10−2～10 cd/m2之间，视杆细胞和视锥细胞都活跃，人类视网膜处于中光视觉的过渡模式。因为神经元只能传输一个动态范围大约为1:103的信号。所以人的视网膜工作原理是首先压缩真实场景亮度的动态范围，然后将光感受器适应到一定的亮度水平(即适应水平)，在适应水平附近的一个相当小的动态范围内感知图像。为了描述视网膜对人类亮度感知的反应，提出了各种基于神经科学实验的响应模型。

Naka-Rushton 方程[10]是比较有代表性的响应模型。此方程描述了视网膜响应度R与亮度水平L的关系，具体公式如下：

式中，n为决定视网膜反应函数陡度的参数；σ 为适应水平。

式(1)表示人眼视觉系统中采用以适应水平为中心的S 形曲线函数，此函数将亮度水平转换为视网膜响应度。近几年的视觉映射技术一般都采用类似的S 型曲线响应函数，将现实世界的光亮度转换成像素亮度。采用基于人眼亮度感知的S 型曲线函数，在避免视觉伪影的同时，提高了对比度。

1.2 基于人眼感知的间接方法

许多间接的方法都是利用人的视网膜所能感知到的最小亮度差异(just noticeable difference, JND)来推导变换函数。根据Weber-Fechner 定律，JND(表示为dL/dS)与背景亮度L成正比：

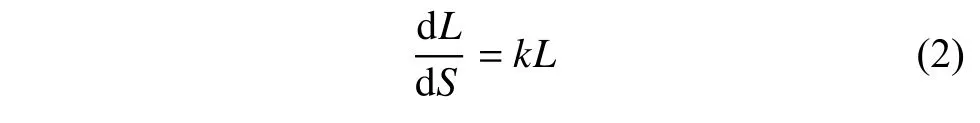
式中，k是一个感知常数，为Weber 分数。求解式(2)的常微分方程可知，感知到的亮度S可表示为：

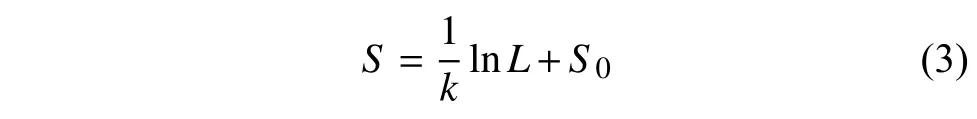
式中，S0是积分常数。各种间接的方法使用对数函数[11]或GC 曲线[12]作为变换函数。然而，由于Weber-Fechner 定律仅适用于亮度大于100 cd/m2的亮度水平[13]，对于低亮度水平下的视网膜响应并不匹配。因此，通常会在黑暗区域导致对比度过度增强。为了解决这一问题，文献[14]提出了一种利用图像直方图确定参数的自适应伽马校正(adaptive Gamma correction, AGC)方法。此方法中变换函数R(L)为：

式中，Lmax为最大像素亮度；CDF(L)为输入直方图的累积分布函数。与其他间接方法相比，AGC方法表现出更好的视觉匹配效果。对于模糊图像，这种效果尤为明显。然而，此方法提高了图像的平均亮度，在亮区损失了一定的对比度。为了解决上述局限性，文献[15]通过修改GC 曲线来构建S 型曲线，但很难同时达到令人满意的对比度增强效果和平均亮度。

为此，文献[16]提出了一种S 型函数的变换函数R(L)，定义为：

式中，C为尺度参数，用来确定增强程度。受此启发，文献[17]通过修改式(5)扩展了文献[14]中的工作，如下所示：

式中，K1和K2是调优参数。虽然这些方法证明了S 型曲线增强对比度的可行性，但它们的性能仍然较差，图像失真严重。

2 基于S 型函数的灵敏度模型

Stevens 幂次定律是一个著名的刺激−反应模型，与Weber-Fechner 定律相比，它涵盖了更广泛的感觉范围。在Stevens 幂次定律中，感知亮度R(L)函数定义为：

式中，指数k取决于刺激的类型。式(7)以微分的形式可写为：

式中，k用作灵敏度参数。此参数决定了随着刺激强度的增加，视网膜响应度增长的速度。对于不同类型的视网膜响应度，k假设为一个常数，即常规GC 曲线。然而，由于人类视网膜响应度是由背景亮度自适应决定的。因此，本文根据亮度感知情况，建立k模型。文献[18]的实验表明，人类视网膜亮度的对比响应度(即Weber 分数)随着对数级亮度的增加呈指数式递减。因此，Weber 分数可以近似拟合为对数级亮度的指数函数。基于这些研究，本文将k建模为以下指数函数：

式中，α 和β 分别为确定k(L)的最大值和陡度的参数。变换函数R(L)为：

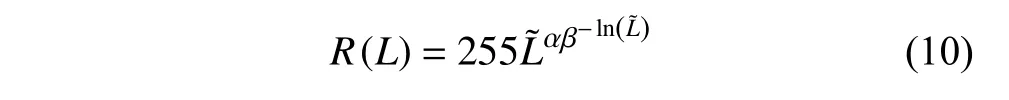
式中，L为原始像素强度，取值范围[0, 255]；为归一化到[0,1]的像素强度，即将单个独立的像素强度处理为与整体图像相关的对比度，具体为：

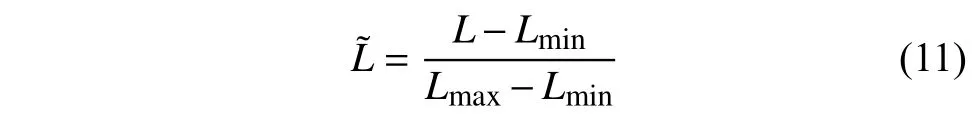
式中，Lmin和Lmax分别为输入图像的最小和最大亮度等级。式(10)中的变换函数覆盖数字图像的全动态范围[R(Lmin)=0,R(Lmax)=255]。

3 自动参数估计

本节分析了式(10)中变换函数的两个参数 α和 β 对合成图像的影响，并引入一种新的自动参数估计方法。首先，将α 从0.3 逐步变化到1.1，每一次的增量为0.2，同时保持β 为2.0，得到的输出图像如图1 所示，当α 增大时，输出图像变暗。由于 α 限制了图像中各点亮度的最大值，可通过控制α 来调节输出图像的平均亮度。但α 需要约束来避免由平均亮度变化[19]引起的图像失真和闪烁伪影。为保持原始图像的平均强度水平，修正变换函数为：

图1 参数α 对输出图像的影响

式中，Lmean为归一化输入图像的平均强度等级。即保证经过转换后的图像平均亮度与原始图像的平均亮度相一致，在此情况下，通过求解式(12)，可得到保持平均亮度的最优α：

β 对输出图像的影响如图2 所示。如图2g 所示，通过式(13)得到的变换函数保持输入图像的平均亮度水平，因而不需要考虑β 值。

图2 参数β 对输出图像的影响

通过确定变换函数的陡度来控制对比度增强程度，当值太小时，此方法的增强性能不理想；如果太大，变换函数会出现陡坡，导致明暗区域的细节丢失明显。因此，为了保持图像细节的同时提高图像对比度的最优值，本文定义：

式中，Ed(β)为数据保真项；Ee(β)为增强项；λ 为控制数据保真项与增强项之间权衡的正则化参数。

为了防止输出像素值被截断而导致信息丢失，Ed定义为离散熵(DE)损失：

式中，p(·)为概率质量函数；hi为原始直方图的第k个分量；ho为使用式(10)在给定β 的条件下得到的输出直方图；N为直方图的分量总数。

对于增强项，本文采用像素区方法来测量图像中所有像素的灰度差。具体为：

式中，N为直方图分量的总个数；i、j表示对应分量的索引。

当图像直方图分布均匀而不集中于特定灰度层时，该项得分较高。为了找到最佳的β，最小化式(14)中的函数E(β)，本文采用黄金分割搜索算法评估算法，估值为三元组的点值形式的黄金比例，逐步缩小搜索范围。本文算法中使用初始区间[1.2,−1.4]来实现迭代过程，直到间隔 βu−βl<10−4或达到最大迭代次数Kmax=500 时停止。

4 实验结果

通过取3 个数据集[20]的550 个测试图像，对比本文方法——基于灵敏度的S 型曲线模型(image contrast enhancement algorithm with S-type function based on human visual system, ICEA)和其他方法。如加权自适应直方图均衡化(weighted adaptive histogram equalizatio, WAHE)、上下文和变分对比(contextual and variational contrast, CVC)[14]、分层差异表示、自适应图像灰度校正(adaptive gamma correction, AGC)[18]、模糊背景对比度增强(fuzzycontextual contrast enhancemen, FCCE)[21]、两 个S型函数的方法[16-17]和其他一些有代表性的直接方法[22-24]。为保证验证的公平性，所有算法都使用Intel i5-3550 3.30 GHz CPU 和16 GB RAM 的台式机测试每个数据集的平均处理时间，使用python进行效果模拟，并且python 的版本和其他依赖库的版本都统一。

为了确定参数α 的最优值，首先在Berkeley图像数据集上测试了本文方法，将λ 从0 改变为0.05，每一步的变化为0.001，如图3 所示。当λ 较大时，本文方法在像素区分数上有很大的改善，但在DE 分数上的细节损失较大。为了实现更好的增强像素区分数，同时防止细节丢失，设λ=0.015。首先将图像转换到HSV 颜色空间，以防止颜色失真，对亮度通道V 进行处理，H 和S 通道保持不变。

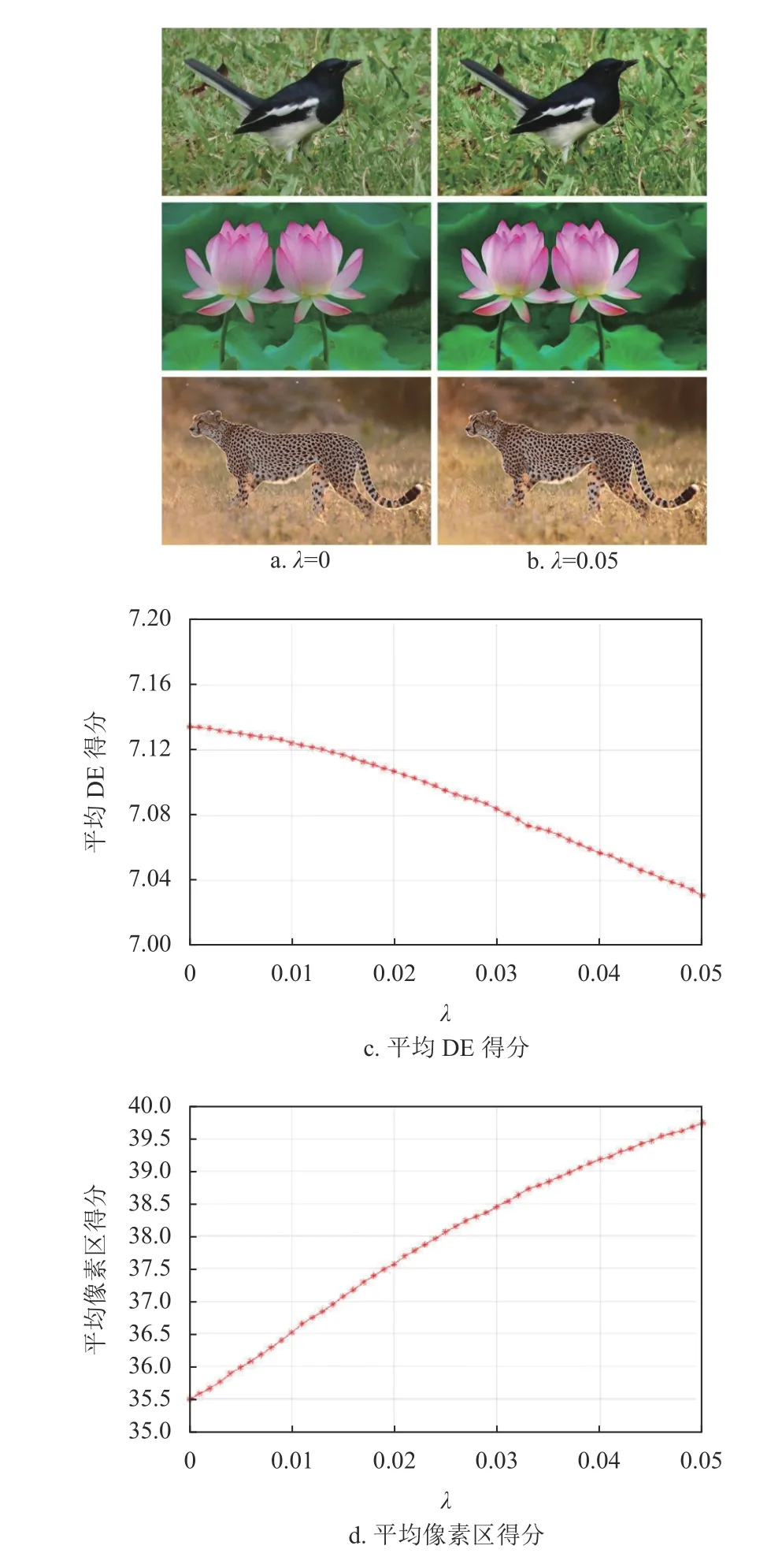
图3 λ 对Berkeley 图像数据集增强图像的影响

为了进行客观评估，本文采用了对比度增强(enhancement measure evaluation, EME)[2]、绝对平均亮度误差(absolute mean brightness error, AMBE)[25]、梯度大小相似度偏差(gradient magnitude similarity deviation, GMSD)[26]和离散熵(discrete entropy, DE)措施。

首先，使用EME 测量基于Weber 算法的图像平均对比度，越大说明图像整体的对比度越好。对于EME，将增强后的图像X划分为N个子块Xi,j，其大小固定相同，W为横向子块的个数，H为纵向子块的个数，计算每个子块的灰度最大值与最小值之比。然后计算平均比例作为最终得分。EME 为：

式中，max(xi,j)和min(xi,j)分别是子块xi,j中像素强度的最大值和最小值。δ 设定为0.000 1，目的是为了避免除零操作；每个子块的大小为8×8。

其次，测量输入图像和增强图像之间的平均像素强度的绝对差值为：

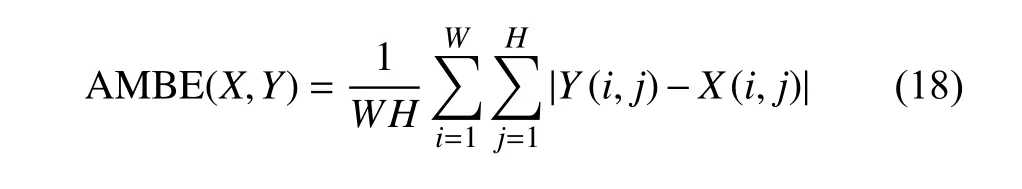
式中，Y是输入图像；X是增强后的图像；其他参数如之前所述。AMBE 评分越低，说明相应的增强方法有效地保持了输入图像的平均亮度，增强后的图像更好地还原了原始图像的整体亮度特性，对人眼有更好的适应性。

再使用GMSD 计算输入图像和增强图像之间像素的梯度相似度，然后测量整体梯度相似度的标准差作为最终得分。GMSD 得分越低，说明输入图像与增强图像之间的图像失真越小：

式中，GMS(i)为第i个子块的梯度幅值相似性；GMSD 是全部局域梯度场的平均处理结果。

最后，使用DE 评估图像中的信息量。DE 值高表示图像包含更多信息。由于信息处理不等式的存在，利用全局变换函数生成的输出图像的DE 不能高于输入图像。

总的来说，直接算法整体比间接算法在人眼观测的效果上更好，特别是在对细节信息的保留上有更好的表现。其中LDR 等间接算法在极大地增强细节的同时会产生光晕的效果。在图像中对比度较强的区域，颜色过于鲜艳，影响图像的整体效果。

表1～表3 为依据文献[20]的3 个数据集，对常见图像处理算法进行分项指标计算的实验结果。结果表明，本文算法表现出了一定的优势。根据EME 结果，LSCN 和本文方法在各个类别中表现出了最好的性能，避免了AMBE 和GMSD 评分中显示的平均亮度变化和图像失真。但是，LSCN 会导致GMSD 分数中明显的图像失真，需要更高的计算复杂度。此外，RSIE 的性能与本文方法相当，但计算复杂度高出约50 倍。

表1 Database 1

表2 Database 2

表3 Database 3

在传统的间接方法中，LDR、FCCE 和EACE在EME 评分方面体现了高对比度。然而，如AMBE评分所示，LDR 在平均亮度保持方面表现较弱。对于EACE 和FCCE，输出图像GMSD 得分显示图像失真严重。相比之下，从EME 评分来看，本文方法的增强性能比第二优的EACE 算法提高了10.5%。此外，AMBE 和GMSD 评分显示，与EACE 相比，此方法平均亮度变化减少60.2%，图像失真减少76.9%。如DE 得分所示，在间接方法中，本文方法是保存细节方面效果第二的方法。虽然FCCE 提供了最高的DE 分数，但FCCE 包含了局部处理，其中输出像素强度是结合输入像素强度和变换函数结果自适应获得。另一方面，此方法在不进行任何局部处理的情况下，仅获得了较一般的DE 得分。

本文方法实现了更高的对比度增强性能，降低了平均亮度的变化，需要更少的计算复杂度，实现了较低的图像失真。

5 结 束 语

基于人视网膜对光感受的对比敏感度，本文提出了一种新的基于S 型函数的对比度增强方法。将对比敏感度建模为对数参数的指数函数，并利用对比敏感度模型导出了一个S 型函数，利用逐步变化的方法估计了此方法的最佳参数。此方法在使图像对比度最大化的同时，防止了信息的丢失，不仅具有较低的计算复杂度，且在对比度方面优于现有方法。面向对比度增强和平均亮度(细节)保持的变换函数，本文方法简单有效，可以应用于其他类型的图像处理，如色调映射以及微光图像增强。在未来的工作中，可尝试利用局部结构信息(如视网膜理论、二维直方图或梯度分布)来进一步提高此方法的细节保持性能。