基于ARIMA－BP组合模型的城市公交客运量预测

刘 昶，吴君华，张凤娇，于多友

（南京林业大学 汽车与交通工程学院，南京 210037）

0 引 言

现如今，城市公共交通是城市基础设施的重要组成部分。在中国的经济发展、城市建设和社会生活中发挥着重要作用，直接关系到城市的经济发展和居民的生活，对城市经济发展有主导性的影响。但是，随着城市化进程的推进，机动车数量不断增加，出现了道路拥堵、堵塞等城市交通问题。优先发展城市公共交通，调整优化城市交通结构，对解决城市交通问题具有重要意义。由于公共交通系统的复杂性和可变性，客运量预测通常是不科学的，因此有必要更好地预测公交客流量，为城市规划提供更好的参考。

然而，城市公交客运量数据的收集存在大量未知、不确定因素和干扰。例如，人口密度、人口流动等能够真实反映客运量、特征和分布规律的历史数据很难获得，也没有形成有效的历史数据。为此，许多专家学者对公交客流量预测方法进行了大量研究，并采用了不同的研究方法进行预测，每种预测方法都各有优缺点。因此，研究城市常规公交客运量预测方法，选择最合适的城市可持续发展方式，具有重要的理论和实践价值。

本文在ARIMA预测模型和BP预测模型的基础上，引入了基于方差倒数法的组合模型算法。以南京地铁客运量为例，首先利用训练样本数据对两种单一模型进行预测训练，随后基于两种单一模型的预测结果，运用方差倒数法，确定两种单一预测结果各自的权重，得到加权组合模型，最后进行预测试验，并给出了相关结果及分析。

1 单一模型预测

1.1 ARIMA模型预测

ARIMA模型是一种时间序列预测方法，其将非平稳时间序列转化为平稳时间序列，然后将因变量的滞后值以及随机误差项的现值进行回归所建立的模型。

ARIMA（，，）中，AR是“自回归”；I为差分；MA为“滑动平均”；为自回归项数；为使之成为平稳序列所做的差分次数（阶数）；为滑动平均项数。自相关系数可决定的取值，偏自相关系数能够决定的取值。

自回归模型（AR）描述历史值与当前值的关系，用变量自身的历史时间数据进行预测，必须满足平稳性的要求，并具有自相关性，只在自相关系数小于0.5的情况适用。阶自回归定义如式（1）：

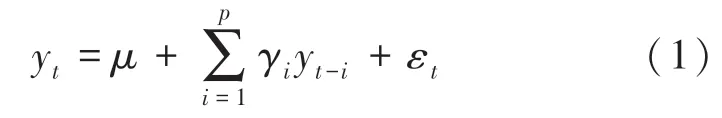
其中，y是当前值；是常数项；为阶数；y是自相关系数；是误差；y为y前的值。

移动平均模型（MA）关注的是自回归模型中误差项的累加，能够有效地消除预测中的随机波动。阶回归的定义如式（2）：

自相关函数（）反映了同义序列在不同时序取值之间的相关性，如式（3）：

ARIMA（，，）模型的一般形式如式（4）：

其中，∇＝（1）为高阶差分；（）1…－φ B为平稳可逆模型的自回归多项式系数；（）1…－θ B为平稳可逆模型的移动平滑系数多项式。式（4）可简化为：

其中，ε是白噪声序列，是时间序列x的均值。

本文以2006～2014年南京客运量为训练数据，对2015～2018年的客运量进行预测，与真实值进行比较，并对模型预测结果进行比较分析。南京地铁客运量年度数据见表1。

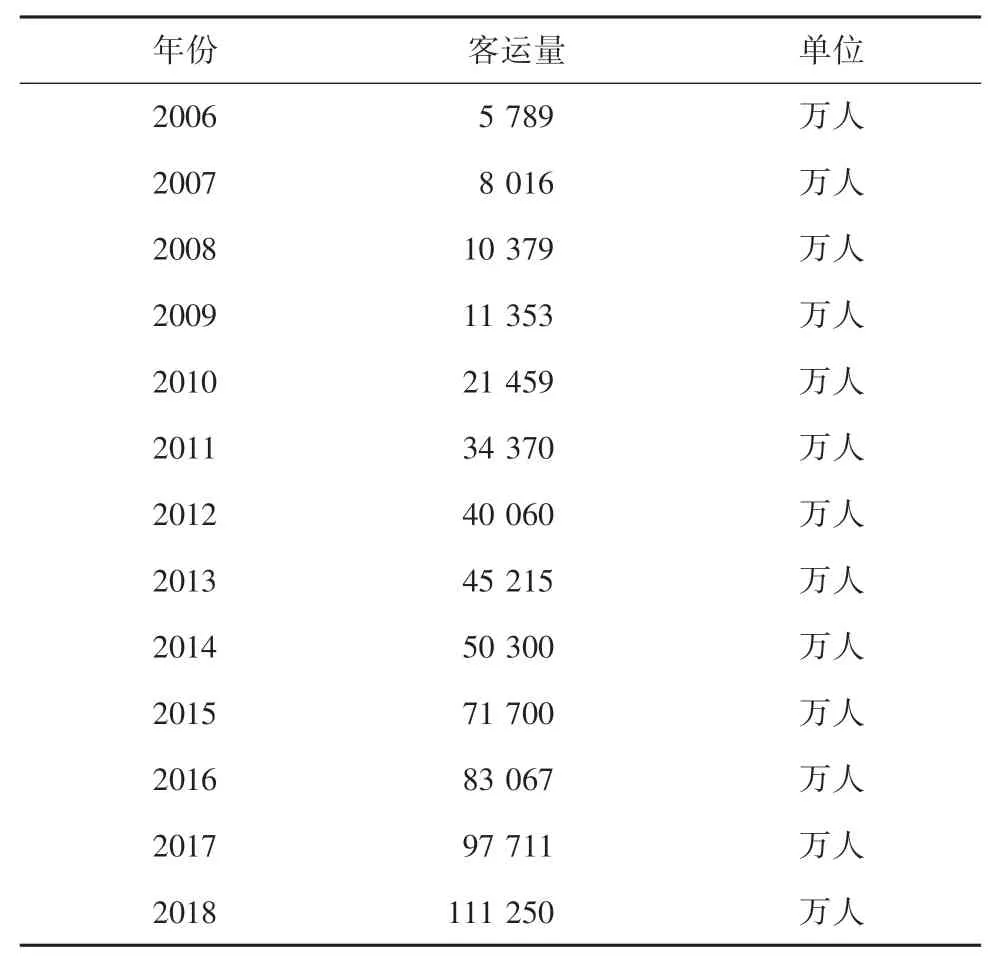
表1 南京地铁年度客运量Tab.1 Annual passenger volume of Nanjing Metro

由训练数据进行预测训练，选用ARIMA（3，0，3）模型，如图1所示。

图1 ARIMA（3，0，3）模型Fig.1 ARIMA（3，0，3）model

预测结果如图2所示。

图2 ARIMA预测结果Fig.2 ARIMA model prediction results

1.2 BP模型预测

BP（Back Propagation）网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前使用较为广泛的一种参数学习算法。

BP神经网络分为两个过程：工作信号正向传递子过程和误差信号反向传递子过程。在BP神经网络运算中，单个样本有个输入、个输出。其输出结果采用前向传播，误差采用反向传播方式进行，在输入层和输出层之间通常还有若干个隐含层。

Robert Hecht－Nielsen在20世纪90年代就已证明：对于任何闭区间内的一个连续函数，都可以用一个隐含层的BP网络来逼近，这就是万能逼近定理。所以一个3层的BP神经网络就可以完成任意的维到维的映射，即这3层分别是输入层（Input）、隐含层（Hidden）和输出层（Output）。输入层接收数据，输出层输出数据，前一层神经元连接到下一层神经元，收集上一层神经元传递来的信息，经过“激活”把值传递给下一层。其工作模式如图3所示。

图3 BP神经网络Fig.3 BP neural network

图3中，是输入层；是隐含层；是输出层；、分别表示输入和输出；为权重；为偏置；每个圆圈表示一个神经元。

通常用来估量模型预测值与真实值不一致程度的损失函数有两种：函数和函数。

由于函数是一次函数，并且随着自变量的增大而增大，同时方便在求梯度时求导，没有值的大小限制，且求导较为容易，常用在回归中使用。因此，本文选用函数作为激活函数。

同样以2006～2014年的客运量为训练数据，对2015～2018年的客运量进行预测，与真实值进行比较，对模型预测结果进行比较分析。

由训练数据进行预测训练，得到的预测结果如图4所示。

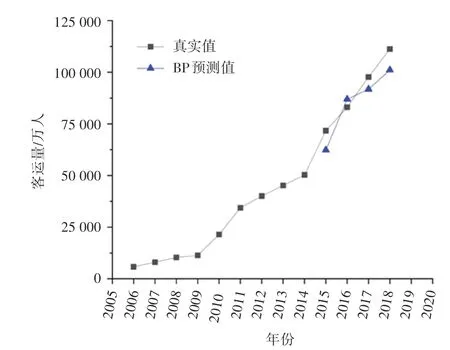
图4 BP预测结果Fig.4 BP neural network prediction results

2 组合模型预测

本章将在两个单模型预测所得结果的基础上，根据两种结果与真实值的误差，设计一种组合模型，对客运量进行预测。

2.1 组合模型构建

本文提出的基于ARIMA模型和BP模型的组合模型的设计思路如图5所示。

图5 组合模型Fig.5 Combined model

求解两种单个模型各自权重的方法如式（6）：

其中，S为第年的客运量真实值；R为ARIMA模型第年的预测值；D为第年ARIMA模型的预测误差；R为ARIMA模型第年的预测值；D为第年ARIMA模型的预测误差；w为ARIMA模型的权重；w为BP模型的权重。

本文利用误差取平方的方式，将两种单一模型的预测误差程度放大，再将几年的误差平方取均值。以该平均值作为确定权重的依据，根据公式求得两种模型各自在组合模型中的权重，从而使组合模型的预测结果更加准确。

2.2 组合模型预测结果

使用上述组合模型，同样以2006～2014的客运量为训练数据，对2015～2018年的客运量进行预测，与真实值进行比较，并对模型预测结果进行比较分析。

由训练数据进行预测训练，得到的预测结果如图6所示。

图6 组合模型预测结果Fig.6 Combined model prediction results

3 预测结果对比分析

本节对ARIMA模型、BP模型以及组合模型的预测结果进行对比分析，其结果如图7所示。

图7 预测结果对比Fig.7 Comparison of prediction results

得到3种模型预测结果的年均误差率见表2。

表2 预测结果年均误差率Tab.2 Annual average error rate of forecast results

由表2中结果可以看出，组合模型预测结果的年均误差率明显低于两种单一模型。

4 结束语

本文基于ARIMA模型和BP模型，设计了一种组合模型预测城市地铁客运量的变化趋势，利用误差取平方的方式，将两种单一模型的预测误差程度放大，再将几年的误差平方取均值，以该平均值作为确定权重的依据，以进一步使误差相对较大的模型获得一个相对较小的权重，而误差相对较小的模型获得一个相对较大的权重。本文以年均误差率为标准，通过实验结果的对比分析表明：组合模型相对于两种单一模型具有更高的预测准确度。