基于改进NSGA－II混合算法求解多目标柔性作业车间调度问题

陆科苗，何利力

（浙江理工大学 信息学院，杭州 310018）

0 引 言

传统的作业车间调度问题（Job－shop scheduling problem，JSP）一直被大家广泛关注，柔性作业车间调度问题（Flexible job－shop scheduling problem，FJSP）是此类问题的一种扩展。简而言之，其是一类满足任务配置需求和条件约束的组合优化问题。求得符合各项要求的最优解，可用于指导实际生产，所以对其研究具有重要的实际参考价值。

多年来，如启发式算法、禁忌搜索（TS）、粒子群法（PSO）、遗传算法（GA）和变邻域搜索（VNS）等算法及混合优化算法，都被广泛用于求解该问题。Amjad通过研究发现，GA方法是解决FJSP最广泛、有效的算法之一。但经典GA中，不同的交叉概率和变异概率会极大影响算法行为和性能，进而影响其算法收敛性。侍守创等提出，将遗传算法与量子粒子群优化算法混合，改善单一算法收敛性不足的问题。吴秀丽等提出基于NSGA－II算法，来求解多目标调度问题。张超勇设计了一种改进的非支配排序遗传算法，优化了精英选择策略。Sevkli等采用变邻域搜索算法，设计了两种不同的邻域结构，组成邻域结构集求解JSP。

从上述研究可以看出，单一算法因其搜索效率低以及进化速度慢，难以进化出较为优质的个体，并存在局部搜索性不足的问题。故采用混合优化算法取长补短求解FJSP，逐步改良求解过程，最终寻得最优解。当前研究多为NSGA－II算法求解多目标优化问题，虽然已经表现了良好的求解能力，但在保持种群的多样性和局部搜索方面仍存在不足。因此，本文结合改进的NSGA－II算法全局搜索性能较强和VNS算法邻域搜索性能较强的特点，提出一种改进的NSGA－II算法和变邻域搜索算法相结合的IVNSGA－II算法。通过与其它算法求解FJSP的实验结果进行比较分析，验证了算法的有效性和适用性。

1 FJSP模型

1.1 问题描述

FJSP可描述为个待加工的工件集合{，，…，J}在台不同的设备集合{，，…，M}上加工。每个工件有若干道工序集合，每道工序有若干台设备可以选择，工序的加工时间也因设备的选择而有所不同，且工序间有先后约束，给定各工序加工时间，确定设备所有工件的加工次序和加工时间。柔性作业车间调度问题的符号定义见表1。

表1 符号定义Tab.1 Symbol definition

在FJSP的调度过程中，应满足以下约束条件：

（1）一道工序只能在一台可选设备上加工；

（2）同一工艺路线上的两个工序不能同时加工；

（3）同台设备同一时刻只能加工一道工序；

（4）加工过程中不能中断；

（5）不同工件具有相同的加工优先级；

（6）同一工件的工序具有先后约束，不同工件之间没有先后约束。

1.2 多目标优化模型

本文以最大完工时间、生产总能耗、设备总负荷最小，作为FJSP的多目标优化函数。其优化模型为：

（1）最小化最大完工时间：最大完成时间是指所有部件同时进行加工，最后一个部件完成时所花费的时间。时间越短，表明方案越好。计算公式如下：

（2）最小化生产总能耗：在车间实际生产中，计算生产总能耗时需要考虑到设备加工和等待加工，两种情况分别对应的单位能耗值是不同的。设备的能耗和车间生产总能耗公式如下：

（3）最小化设备总负荷：车间生产加工时，在满足加工能耗与最大完工时间最小的同时，还要考虑到设备的总负荷。因此，工序在能耗相同的情况下，选择加工时间短的设备，使其设备总负荷最小化。计算公式如下：

2 算法设计

2.1 编码

在对FJSP进行编码时，需要同时考虑到工序、设备的排序问题。因此，本文采用工序与设备融合并行双链式编码方式。第1层为基于工序的编码层（Operation Sequence，OS），第2层为基于设备选择的编码层（Machine Sequence，MS）。融合两种编码方式，形成一条染色体，就可以得到面向FJSP的一个可行解。如图1所示，层的数字表示工件号，工件号出现的次数即表示该工件的第几道工序；层则按照工件工序顺序排列并与之相对应，表示相应位置工序的设备选择。层和层的长度相等。

图1 并行双链式编码示例图Fig.1 Example of parallel double－chain coding

图1中表示的加工顺序为：工件1的第一道工序在加工设备1上加工→工件3的第一道工序在加工设备2上加工→工件2的第一道工序在加工设备2上加工→工件3的第二道工序在加工设备为5上加工依次类推。这种编码方式保证了后续操作所产生染色体解的可行性，且对工件的工序长度和工件数量无任何要求，避免了后续繁杂的修正操作，简单灵活。此外，对其中一层的单独操作不会影响到另一层，具有很强的并行性。

2.2 解码

对和层分别进行解码，目标是根据编码层的形式获得空间范围内优质的解。然而在实际任务分配过程中，常常存在两个相邻工序间等待时间过长，所以可将后续符合相应约束条件的工序，提前插入到符合条件的时间区间中，进行“插队”操作。因此，提出一种最优插入法，实现对解的高效搜索。实现步骤如下：

判断是否为此工件的首道工序，若是则将0作为空闲起点；反之，将上一道工序的完工时间作为空闲起点；

寻找空闲起点之后大于等于待加工工序加工时间的空闲时间段。若未找到，则按顺序正常加工；

选择满足待加工工序加工时间且最短的空闲时间段插入；

重复Step1－3，直至所有工序安排完成；

计算最大完工时间。

最优插入法的插入过程如图2所示。工序O将在设备上加工，根据当前情况，3段可选空闲时间段均满足O的加工时间所需条件。其中空闲1结束时间与工序O结束时间之差所求的空闲时间小于O的加工时间，不满足约束条件舍去；空闲2、3都满足插入条件，而空闲2的空闲时间更短，因此选择空闲2插入。该策略能够为后续工序的插入提供更多的选择，以获取更优质的解。

图2 最优插入示意图Fig.2 Schematic diagram of optimal insertion

2.3 种群初始化

NSGA－II算法中，初始化策略影响着解的质量与收敛速度，是重要的起步阶段。考虑到算法复杂度和种群数量大小限制，在种群初始化阶段，数量规模控制在原种群数量的1.5倍。为保证种群多样性，对于OS编码层采用随机选择产生，随机搜索时种群越大找到最优解的概率也就越大；对于MS编码层采用全局选择、局部选择和随机选择的方式初始化。

将随机式初始化和混合式初始化方式相结合，相互取长补短，在保证收敛速度的同时增强全局搜索能力，经过后续处理迭代，提高初始种群丰富度，减少随机性，加大求得最优解的概率。

2.4 选择算子

本文以最大完工时间、生产总能耗、设备总负荷最小作为FJSP问题的目标，对个体的适应度进行评价，算法的适应度如下：

其中，、、分别为式（1）、式（3）、式（4）的最小化目标优化函数。需要均衡3个适应度指标，根据计算后的适应度，对个体进行非支配排序，同时计算处于同一支配层级的个体拥挤度。种群中适应度最大的染色体直接复制到新种群，然后新种群中的其它个体采用动态拥挤度算法并结合精英解保留策略，选择个体组成新父种群。

2.5 交叉操作

（1）OS交叉：采用基于工件顺序的交叉（POX）如图3所示。父代染色体与进行交叉，交换染色体中工序的位置得到子代。

图3 OS交叉Fig.3 OS cross

（2）MS交叉：采用多点交叉如图4所示。父代染色体和分别选择随机位置，将所选位置按顺序插入子代，然后将剩余未选中位置插入到子代，同理操作。

图4 MS交叉Fig.4 MS cross

2.6 变异操作

变异操作可以起到扩大随机性的作用，增加算法的搜索能力，变异操作如图5所示。在进化初始阶段，需要较小的变化概率，并尽可能多的保留优良基因；而在后期阶段，需要适当增加变异概率产生基因的多样性，以免“早熟”现象，所以在迭代过程中使用动态自适应变异概率。计算公式如下：

图5 OS和MS的变异操作Fig.5 Mutation operations for OS and MS

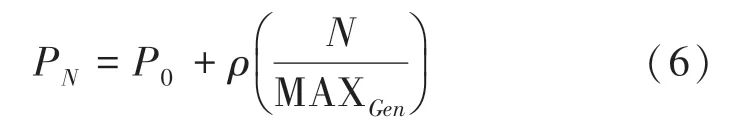
其中，为初始变异概率值；为最大变化率；MAX为最大迭代次数；为当前迭代次数。

2.7 变邻域搜索算法

虽然交叉、变异操作在一定程度上可以增加种群多样性，但算法仍可能存在陷入局部最优的情况。因此，引入变邻域搜索算法，通过改变当前解染色体的某些基因位值，产生邻域可行解，从而避免种群进化过程中产生的解陷入局部最优。本文针对OS染色体段，结合改进的NSGA－II算法中各类算子，再引入4种（insert算子、inverse算子、swap算子、pairwise算子）不同的邻域搜索结构，实现动态邻域搜索，扩大局部搜索范围，增强局部搜索能力。

（1）insert算子：随机选择2点工件所在工序对应的基因位置进行操作。例如位置2、6，则把6位置的基因插入2基因后的位置上，原来的3－5基因往后顺延，具体的结构变换过程如图6所示：

图6 insert算子邻域变换示例Fig.6 Insert operator neighborhood transformation example

（2）inverse算子：随机选择两个位置，将位置之间的工序基因顺序进行反转。例如，选择位置3、7，具体结构变换过程如图7所示：

图7 inverse算子邻域变换示例Fig.7 Inverse operator neighborhood transformation example

（3）swap算子：随机取两个位置，执行两点交换操作。例如，选择位置4、6，具体结构变换过程如图8所示：

图8 swap算子邻域变换示例Fig.8 Swap operator neighborhood transformation example

（4）pairwise算子：将相邻的两个成对基因位置互换，即第一个和第二个基因互换位置，第三个和第四个基因互换位置，以此类推，最后若剩下单个工序则不变动。具体结构变换过程如图9所示：

图9 inverse算子邻域变换示例Fig.9 Inverse operator neighborhood transformation example

2.8 IVNSGA－II算法

本文提出的IVNSGA－II算法，是以改进的NSGA－II算法为基础，通过非支配排序、动态拥挤度算法和精英选择策略得到新种群，再结合VNS变邻域搜索算法构建邻域结构集求解多目标柔性作业车间调度问题，算法流程如图10所示。IVNSGA－II算法流程如图10所示：

图10 IVNSGA－II算法流程Fig.10 IVNSGA－II algorithm flow

3 实验结果与分析

IVNSGA－II算法通过MATLAB编程实现，在win10系统，Intel（R）Core（TM）i7－8565U CPU＠1.80 GHz，内存8 GB的计算机上实现。各项参数设置为：种群规模P＝150，最大迭代次数MAX＝100，交叉概率P＝0.8，变异概率0.05。

为验证IVNSGA－II算法的可行性和有效性，分别进行单目标优化和三目标优化实验。其中，单目标为最大完工时间。采用Brandimarte设计的5个典型FJSP数据集（mk01～mk05）进行测试对比，此数据集中包括不同的工件数、工序数、设备数以及加工时间。车间使用的加工设备功率相关数据见表2。

表2 设备功率表Tab.2 Equipment power table

3.1 单目标实验

表3为GA、PSO、NSGA－II、IVNSGA－II算法在mk01～mk05中运行的结果。根据对比可以看出，IVNSGA－II均取得最优解，证明了该算法具备良好的性能。

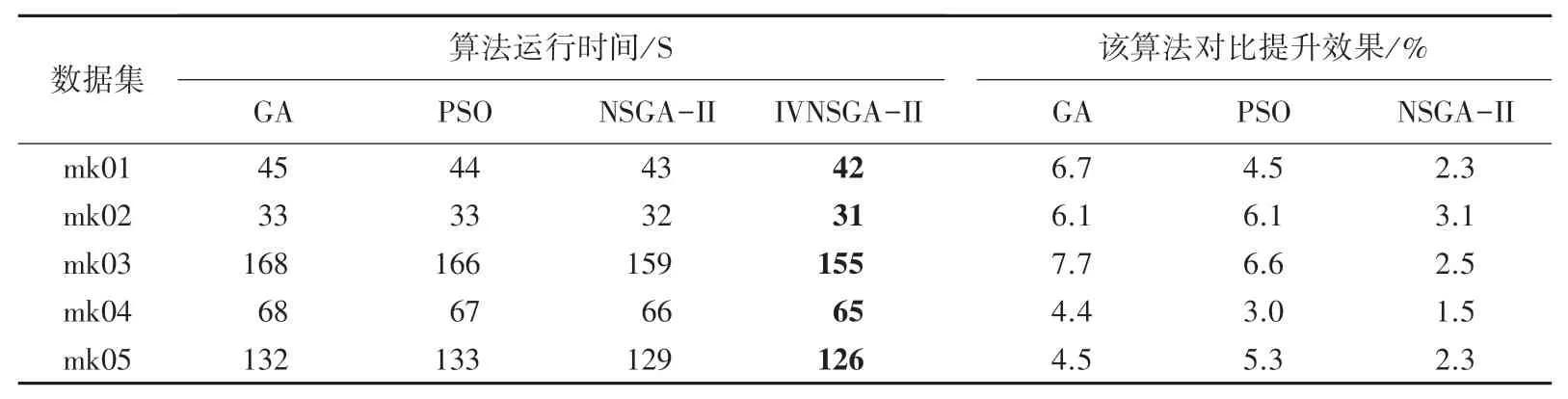
表3 算法运行时间结果对比Tab.3 Comparison of running time of different algorithm

以mk01为例，其收敛曲线如图11所示。由图可见，开始迭代时下降速度较快，说明开始采用的初始化策略加速了收敛速度，大概在40代时得到最优解；之后的上下波动，证明IVNSGA－II算法避免了陷入局部最优解。mk01的调度甘特图如图12所示。

图11 IVNSGA－II迭代收敛图Fig.11 IVNSGA－II iterative convergence graph

图12 mk01调度甘特图Fig.12 mk01 scheduling Gantt chart

3.2 三目标实验

同等条件下在mk01数据集上进行实验，结合设备功率表，针对最大完工时间、生产总能耗以及设备总负荷的三目标求解，得到完整的Pareto前端。不同于单目标的衡量指标，解的数量也是衡量多目标调度性能的重要指标之一。本文将IVNSGA－II与NSGA－II进行三目标性能对比，对比结果如图13所示。

图13 三目标Pareto前沿图Fig.13 Three－target Pareto frontier map

从图中可以看出，3个目标之间相互影响，IVNSGA－II所获得解的范围更大，解的个数更多，解集质量也更优。可以证明，IVNSGA－II具有良好的全局收敛性和局部搜索性。在实际调度生产中，企业可以根据实际情况选择合适的解，然后获得相应的甘特图，用于指导实际生产。

4 结束语

本文针对FJSP问题，同时考虑多目标优化的特点，以最大完工时间、生产总能耗、设备总负荷最小为优化目标，提出一种IVNSGA－II算法，对多目标优化问题求解。通过动态拥挤度和自适应变异算子，保证求解过程中解的多样性；再结合VNS算法邻域搜索能力，设计4中不同的邻域结构进行变邻域搜索。通过在Matlab平台上实例的分析对比，表明该算法可有效解决FJSP问题，为车间生产者提供可参考的调度方案，且具有较好的稳定性和寻优能力，验证了所提算法的有效性。