基于置乱-扩散与新型组合混沌系统的图像加密算法
王庆杰,李国东,2,安博文
(1.新疆财经大学 统计与数据科学学院,新疆 乌鲁木齐 830012;2.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;3.成都理工大学 商学院,四川 成都 610059)
1 引言
随着当前网络技术、大数据、5G 时代等技术的迅猛发展,人类传输信息的方式也在随之改变。由于数字图像在一定程度上可以更好地表达信息,使得信息通过数字图像来传输有了极大的应用。再结合新冠肺炎疫情防控局势依然严峻的今天,数字图像的传输以及应用的范围有了空前增加。由于数字图像可能带有大量的隐私以及机密级别的信息,从而数字图像的存储以及传输将受到被截获以及盗取、破解等方面的威胁。
由此,对数字图像加密研究的重要性就日益凸现出来,通过对数字图像进行加密或者压缩、嵌入等方式实现加密传输。从而各种数字图像的保护技术呈现出来。目前基于Logistic 映射的图像加密算法有学者进行了研究。Wang Xingyuan 等[1]利用一维Logistic 自嵌入混沌系统产生,结合置乱和扩散操作的混沌图像加密算法;李春彪等[2]等在经典Logistic 映射中引入正弦反馈,以此来进行图像加密;Manish Kumar 等[3]基于一维Logistic 映射,提出了一种新的、快速、安全的医学图像加密算法;Chanil Pak 等[4]提出了一种新的二维改进Logistic 耦合映射,并应用于图像加密;目前基于Chebyshev 映射的图像加密算法有学者研究成果。Ali Shakiba[5]在一维混沌Chebyshev 映射基础上构造了一种新的随机混沌图像加密算法;Borislav Stoyanov 等[6]提出了一种基于Chebyshev 映射和旋转方程的新型图像加密算法。
还有很多学者通过将logistic 映射和Chebyshev 映射与其他混沌系统相结合应用在图像加密领域,从而由此产生了许多新型组合混沌系统。钟艳如等[7]等通过将Sine 与Chebyshev 进行组合得到了新型2D Chebyshev-Sine 混沌系统,并应用在了图像加密上;孙树亮等[8]通过将Logistic 与正弦映射进行组合得到了新型2D Sine-Logistic 混沌系统,并应用在了图像加密上;还有许多学者也做出了不同混沌一起应用在图像加密上的研究[9-16]。图像的加密研究目前主要集中于对图像采取的置乱和扩散加密流程以及多次置乱与扩散相结合的加密流程。胡春杰等[17]等人提出了改进Arnold 映射二次置乱的图像加密算法;文小爽等[18]等提出了基于置乱与扩散的彩色图像加密算法;张芳君等[19]等提出了基于混沌序列置乱与扩散变换的彩色数字图像加密算法。
传统混沌系统的图像加密算法通常基于应用广泛的低维混沌系统来产生混沌,以此对所需加密的图像进行相应的置乱或者扩散操作,从而达到图像在传输过程中的加密处理。但是,由于低维混沌系统其本身的初始参数较少、构造简单、密钥空间较小等优点也在日益发展的今天变成了它的缺点,并且单一混沌也有一定的局限性。为了进一步利用低维混沌系统以及解决单一混沌系统的不足,本文通过将Chebyshev Map 与Logistic Map 进行组合,构造了新型三维组合混沌系统 (3D Logistic-Chebyshev Chaotic Systems,3D-LCCS),并设计了一种融合多次置乱、扩散的图像加密算法,以期为图像加密领域提供算法新形势的参考以及提高图像加密领域的安全性。
2 基本理论
在基于混沌系统的图像加密算法中,一维映射由于本身简单的构造产生了广泛的应用。本文通过将应用广泛的Logistic Map、Chebyshev Map 进行组合,得出了构造了新型三维组合混沌系统(3D Logistic-Chebyshev Chaotic Systems)。
2.1 Logistic Map 定义

控制参数η 的取值范围为:0≤η≤4。
2.2 Chebyshev Map 定义

其中控制参数β 的取值范围为:0≤β≤4。
2.3 3D-LCCS 定义
本文通过将构造简单、维度较低的Logistic Map、Chebyshev Map 进行组合,在前人文献[16]的基础上改进得到了新型三维组合混沌系统 (3DLCCS)。

其中控制参数u 的取值范围为:0≤u≤1。
通过上式(3)可看出本文通过将Logistic Map、Chebyshev Map 进行组合得到了3D—LCCS。通过Matlab 软件对3D—LCCS 进行仿真,可得知该混沌系统具有正的李雅普诺夫指数。通过观察混沌系统的混沌解的轨道图以及分岔图可以发现,该混沌系统的复杂度以及混沌特性具有很好的体现,同时也表明该混沌系统具有更好的遍历性。混沌系统的轨道图和分岔图分别如图1 和图2 所示。

图1 3D—LCCS 轨道图

图2 3D—LCCS 的分岔图
3 图像加密与解密算法
本文通过将构造简单、维度较低的Logistic Map、Chebyshev Map 进行组合,重新构造了新型三维组合混沌系统(3D—LCCS)。在一定程度上克服了低维混沌或者是单一混沌系统的密钥空间小、构造简单、初始参数较少等局限性。在应用新型三维组合混沌系统的基础上,结合多次图像置乱以及扩散操作来达到对明文图像的加密处理,图像加密算法流程如图3 所示。

图3 图像加密算法流程图
图像加密与解密算法具体步骤如下:
Step1:对Logistic Map 和Chebyshev Map 的控制参数进行形式的改变后,重新组合为3D Logistic—Chebyshev Chaotic Systems。
Step2:假设明文图像为P,大小为M×N,M 与N 分别为图像的宽度与长度。对图像的像素值进行求和后再进行取余256,然后再进行取整等操作,此时得到数值的取值范围在(0,1)之间,由此可逐一求出混沌系统的初始值x1、y1、z1、u 的具体值。
Step3:通过将混沌系统的初始值x1、y1、z1、u 带入3D—LCCS,使混沌系统迭代M0+n0次,M0为了消去混沌系统的暂态过程可能带来的不适情况所进行的初始迭代,n0为后续加密过程所需混沌序列的迭代次数,初始迭代的混沌序列应舍去然后利用后n0次迭代的混沌序列进行加密操作。由此可得到用于图像加密所需的混沌序列。
Step4:通过将二维图像展成一维向量后,再结合Step3 所产生的混沌序列,对此时的一维向量进行置乱操作。通过Step3 产生加取模和循环左移的伪随机序列,利用该序列对置乱后的图像进行融合了加取模以及循环左移的操作,由此可得第一阶段的密文图像。

式中,C 为置乱后的密文图像,S 为混沌序列向量,P 为置乱后的一维向量,i=1,2,…,MN,LSB3表示选取数值的最低三位。
Step5:通过将第一阶段的密文图像展开成一维行向量后,利用Arnold 伪随机矩阵进行置乱操作。Arnold 矩阵是整数矩阵,其逆矩阵也是整数矩阵,所以其也常用于图像置乱当中。其定义如下所示。通过Step3 再次产生正向扩散与逆向扩散的伪随机序列,利用该序列对Arnold 变换后的图像进行异或双向扩散操作,由此可得最终的密文图像。

其中,(x1,y1)、(x0,y0)分别为变换前、后的像素点位置,mod 为取模运算,a、b 为整数,M、N 为图像的行数与列数。C 为正逆向扩散后的密文图像,S为混沌序列向量,P 为Arnold 置乱后的一维向量。
Step6:密文图像的接收者,可以依据上述加密操作的逆过程进行解密。
4 实验仿真
图像加密算法仿真实验平台的配置为i5-6300HQ、2.30GHz 的inter处理器,内存大小为7.8G,操作系统为64位的 windows10,Matlab2016a。选取256×256 的Lena 标准灰度图像作为明文图像,设定此时的混沌系统初始值分别为x1=0.92、y1=0.74、z1=0.83、u=0.96,将明文图像带入上述加密算法流程可得到如图4-7 所示的明文图像和密文图像以及解密图像。

图4 明文图像

图5 第一阶段密文图像

图6 最终密文图像

图7 解密图像
5 安全性分析
5.1 密钥空间
密钥空间是用于图像加密算法所有密钥的集合,本文的加密系统密钥分别有x1、y1、z1、u,上述各个参数的初始值取值范围为[0,1],其步长均为10-14,可知密钥空间的大小为1056,可知本文加密系统的密钥空间大于2100,由此得出本文的加密系统可以有效地抵抗穷举密钥攻击。
5.2 密文统计特性
密文的统计特性选用直方图来进行图示说明加密后的直方图是否有了明显的改变,可以图像的直方图来观察像素值的大致分布情况以及统计信息,所以用此检验加密算法的加密效果尤为重要[20]。基于Lena 加密前后的直方图如图8 和图9 所示,结合卡方检验得知密文的检验值为253 远远小于χ20.01(255),并从图中可得出加密后的密文图像直方图分布较为均匀,没有呈现出明显的规律性,攻击者想获取信息有一定的难度。

图8 明文直方图

图9 密文直方图
5.3 相关性分析
通常来说,明文图像的相邻像素点的相关性较强。由此得知从密文图像中随机选取若干相邻像素点,相关性若不强也可得知加密算法的性能。本文通过对明文图像以及密文图像,分别随机选取了2000 对相邻像素点,来检验各自的相关性。其图像相邻像素点相关系数计算结果如表1 所示,明文图像以及密文图像的各自相关情况如图10-17 所示。可得出明文图像的相邻像素点的相关性较强,密文图像的相邻像素点相关性可以认为不存在。

表1 图像相邻像素点相关系数

图10 明文图像水平方向相关情况
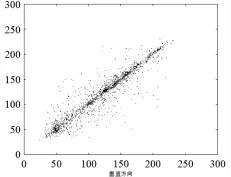
图11 明文图像垂直方向相关情况

图12 明文图像正对角方向相关情况

图13 明文图像反对角方向相关情况

图14 密文图像水平方向相关情况

图15 密文图像垂直方向相关情况

图16 密文图像正对角方向相关情况

图17 密文图像反对角方向相关情况
5.4 抗差分攻击
抗差分攻击就是指明文的敏感性,通过对所需加密的明文进行微小改变然后对比加密后的密文。结合像素改变率 (number of pixels change rate,NPCR) 与归一化平均改变强度 (unified average changing intensity,UACI),NPCR的理论期望值99.6094%和UACI 的理论期望值33.4635%来对比该加密系统的明文敏感性以及能不能抵抗选择明文攻击。

上式中Q1、Q2分别为明文图像P 没有改变以及微小改变后所对应的密文图像,M 与N 分别为图像的宽度与长度[21]。结果如表2 所示,由表中信息可得知本文的加密算法具有抗差分攻击能力。

表2 NPCR 和UACI 的值
5.5 密钥敏感性分析
密钥敏感性分析是为了检验密钥是否具有敏感性。当密钥发生微小变化时,依据此时变化后的密钥再次对明文图像进行加密操作,然后与密钥没有变化时的产生的密文图像进行对比,如果两个密文图像差别非常显著,则得知该图像加密算法的密钥具有一定的敏感性[23]。此时通过对密钥进行微小改变再次对明文进行加密,得到如下所示图18。由图19 也就是密钥改变前、后密文图像的差图呈现出噪声样式,从主观上反映出了两个密文图像差异性显著,也表明了密钥具有敏感性。

图18 密文图像

图19 密文图像差图
5.6 信息熵
信息熵在一定程度上为了测量图像的随机性,熵值如果越大,随机性越大,可得到的信息也就越少。信息熵的计算公式如下所示:
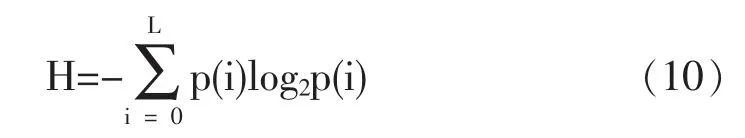
式中,L 为图像的灰度等级数,p(i)表示灰度值出现的概率,H 的理论值为8,本文的信息熵值为7.9972,也是非常接近8,由此可得知密文图像灰度分布也是十分均匀的,加密算法可以抵抗攻击。
6 结语
本文依据现有的Logistic Map、Chebyshev Map进行组合,重新构造出了新型三维组合混沌系统,克服了低维混沌系统、单一混沌系统的结构简单、密钥空间较小等局限性还具有更好的遍历性等优点。设计了基于3D-LCCS 的图像加密算法。在该算法中进一步结合多次置乱—扩散操作,借助Matlab仿真平台,检验了本文提出图像加密算法,复杂度高、密钥空间较大、安全性好,可以抵御各种攻击,对于图像的加密传输具有十分可观的应用前景与价值。

