多周期家庭护理的路径规划与调度算法

黄金瑶，刘同来，吴嘉鑫，武继刚

（广东工业大学 计算机学院，广州 510006）

0 概述

随着我国社会人口老龄化日益加重，老龄群体对家庭医疗护理服务的需求不断提高。研究表明，我国的老年人口将在2050 年达到4 亿以上，其中，上亿人口需接受长期的家庭医疗护理服务［1］（Home Health Care，HHC）。HHC 是一种由家庭护理机构负责管理及分配空闲的医护人员以及医疗设备，为有需要的老人提供一定程度的医疗诊治、生活照料等上门服务，能够减少老人的住院开销，缓解医疗中心的服务压力［2-3］。因此，促进HHC 行业的发展对提高行动不便的老人群体的医疗服务质量具有重要意义。

申请HHC 的的具体步骤：老人首先向家庭护理机构提交一段时间内的服务申请，包括服务日期、服务时长、服务项目等；接着家庭护理机构根据需求为老人合理安排符合要求的护工提供上门服务；最后接到服务任务的护工将在指定时间内从当前所在位置出发到指定的位置为老人提供服务。由此可知，家庭护理路径规划与调度问题（Home Health Care routing and scheduling Problem，HHCP）［4］指的是家庭护理机构在同时满足老人需求和护工工作时间的限制条件下，为护工安排合理的护理路径，使家庭护理机构的服务质量最高的问题。

HHCP 一般可划分为单周期和多周期2 类。单周期HHCP 研究如何为护工安排周期为一天的护理路径［5］，如文献［6］认为护工的工作时间对最终规划路径的适应性存在重要影响，因此研究平衡各个护工的工作时间，但没有考虑多周期的影响。与单周期HHCP 不同，多周期HHCP 则研究如何为护工安排2 天或2 天以上的护理路径［7］。文献［8］在考虑护理连续性约束的基础上研究周期为一周的HHCP 问题，并将原问题分解成多个子问题进行求解。但随着问题规模的增大，多周期HHCP 问题最优解的获取时间呈指数级增长。当问题规模达到一定量级时，使用精确算法无法在规定时间内得到最优解。为保证算法所得到解的时效性，可采用启发式算法对大规模多周期HHCP 进行求解，如文献［9］设计一种变邻域搜索算法来求解具有超时收费、偏好匹配等约束条件的HHCP 问题。文献［10］同时考虑不确定旅行时间、服务时间等因素并应用禁忌搜索算法求解一个长周期HHCP 问题。

目前大部分多周期HHCP 研究工作集中于最大化家庭护理机构的服务质量，这些工作所定义的服务质量由老人的服务需求是否已经满足［11-12］、服务是否及时［13-14］、老人对服务是否满意［15-17］等因素构成。然而除上述因素以外，还存在其他因素影响家庭护理机构的服务质量。例如：当护工拥有更匹配的服务技能或曾经对某一位老人进行过多次护理时，可以有效提高该护工提供给老人的服务质量；考虑到老人在护工选择上的主观因素，老人在申请护理服务时，可根据自身偏好提供一份黑名单，家庭护理机构将不为老人安排名单内的护工；当服务技能、收费、时间等客观因素或黑名单约束未能安排护工给老人提供护理服务时，家庭护理机构的服务质量会因此降低。目前关于HHCP 的相关工作尚未考虑上述因素对家庭护理机构的服务质量影响。

本文提出带服务约束的多周期家庭护理路径规划与调度问题，并证明该问题的NP 难解性。为了在老人提供的黑名单、必选服务技能、服务价格和服务时间的约束下提升家庭护理机构的服务质量，提出一个基于贪心策略的路径规划算法，该算法在满足老人服务约束的前提下，优先为开始等待服务时间最早的老人安排能够提供服务质量最高的护工。在此基础上，提出定制的遗传算法，以获得更优的多周期护工路径规划方案。

1 本文模型

图1 所示为家庭护理机构为老人提供家庭护理服务的过程。本文针对家庭护理机构的护工护理路径规划与调度问题构建数学模型。在本文模型中，假设家庭护理机构进行路径规划的日期集合为D，日期数量为g，护工的数量为a，老人的数量为b。令K={i|1 ≤i≤a}和P={j|1 ≤j≤b}分别表示护工集合和老人集合，设护工i的工作日期集合为老人j的请求服务日期集合为在护工的同一工作日期内，护工可为一名或多名老人提供护理服务，而每名老人每天最多只能由一名护工服务。老人j向家庭护理机构申请的预期服务请求次数为nj，每次请求服务时长都为tj，以及经过安排后一周内实际被服务的次数为zj。

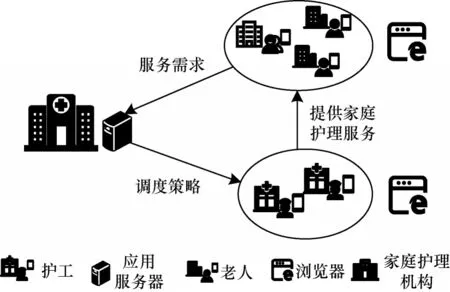
图1 本文家庭护理服务模型Fig.1 Model of home health care in this paper

护理连续程度可反映护工对老人的熟悉程度。对于曾经服务过老人的护工，其为老人提供服务的次数越多，相应的护理连续程度就越高，护工对老人提供护理的服务质量也越高。受文献［18］启发，令函数f(si,j)表示护工i与老人j之间的护理连续程度，其计算公式定义如下：

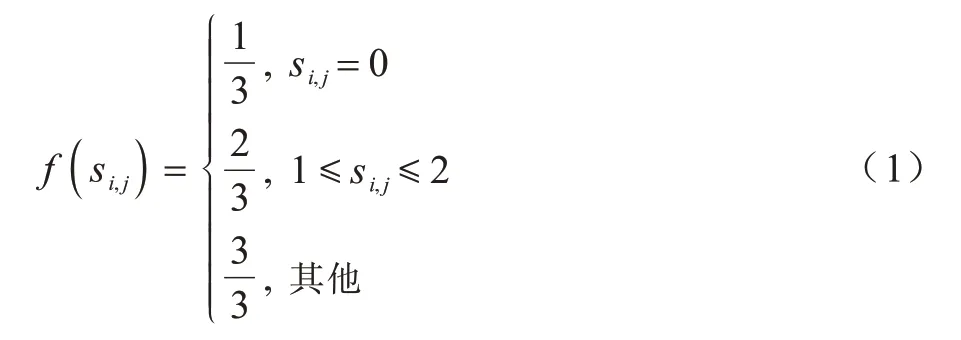
其中：si,j为护工i过去服务老人j的次数。

接下来将详细介绍护工为老人服务所必须满足的约束，包括服务时间约束、服务技能约束、服务价格约束、以及黑名单约束等。本文涉及的符号定义如表1 所示。

表1 符号定义Table 1 Symbol descriptions

1）服务时间约束与护工护理路径的表示

2）服务技能约束

老人j对护工的服务技能需求包括必选技能Mjp和可选技能Oj，其中必选技能意味着服务老人j的护工i的专业技能Mik必须包含Mjp，即Mjp⊆Mik,∀j∊Xid,i∊K。

3）服务价格约束

4）黑名单

老人j向家庭护理机构中心发出护理服务请求时，将会附加黑名单Lj，家庭护理机构将只安排不在该名单内的护工为该老人服务，即：i∉Lj,∀j∊Xid,d∊i∊K。

护工i为老人j提供护理的服务质量由护工i掌握的技能与老人j可选服务技能的匹配度以及护工为老人服务的连续程度f(si,j)2 个部分组成。令Hi,j表示护工i某一次为老人j提供护理的服务质量，可得其中：α1、α2分别表示护工掌握的技能与老人可选服务技能的匹配度的权重，以及护理连续程度对护工服务质量影响的权重。

本文定义家庭护理机构提供给老人的服务质量由以下2 个部分组成：所有护工一周内为老人提供护理的服务质量之和；老人未被满足的服务请求次数（未被服务次数）。

令H表示家庭护理机构提供的服务质量，可得：

其中：α3表示老人未被服务的次数对家庭护理机构服务质量影响的权重。为了统一量纲，本文按照文献［19］引入了系数γ和γ′，其中γ和γ′分别表示每满足一个可选技能可提高的服务质量，以及每未满足一次服务请求所降低的服务质量。

本文所研究的带服务约束的多周期家庭护理路径规划与调度问题（Multi-period Home Health care routing and Scheduling Problem with service constraints，MHHSP）的形式化描述如式（4）～式（10）所示：

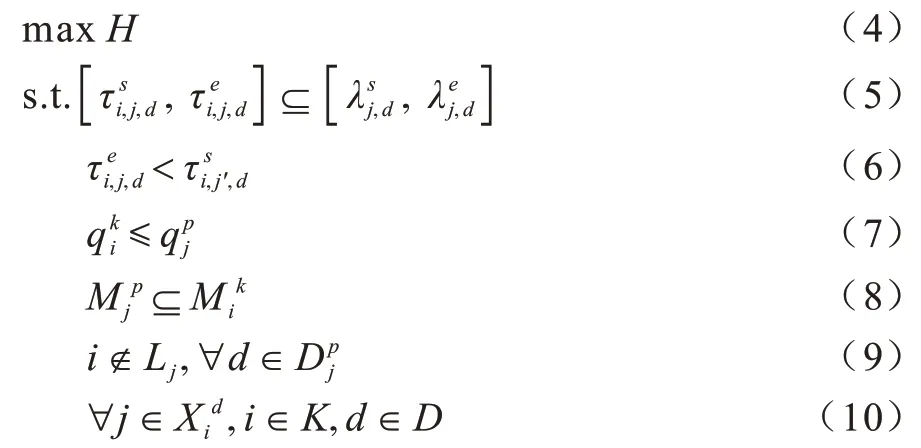
如式（4）所示，MHHSP 的目标为最大化家庭护理的服务质量。式（5）表示护工需在老人的等待时间窗内为老人提供护理服务。式（6）表示在护工所有有序的护理路径中，护工必须按顺序为老人提供服务，即护工i服务路径中的任意一个老人j的结束时间必须在护工i为下一个老人j′服务的开始时间之前。式（7）表示护工的服务收费不能超过老人所能接受的服务价格。式（8）表示护工的专业技能必须满足老人的必选服务技能需求。式（9）表示服务老人的护工必须不在该老人提供的黑名单上。式（10）表示变量i、j和d的取值范围。

定理1本文所提出的家庭护理资源调度和路径规划问题MHHSP 为NP 难问题。

证明本文所提出的家庭护理资源调度和路径规划问题MHHSP 可以归约为多车场车辆路径优化问题（Multi-Depot Vehicle Routing Problem，MDVRP）。MDVRP 具体描述如下：已知客户的位置、车辆的位置以及客户的需求，如何为车辆安排合适的行车路径，使路径成本最小。针对本文所提出的问题构建一个特例，即不考虑式（7）～式（9）。在该特例中，将老人看作客户，护工看作车辆，老人的需求看作客户的需求，最大化家庭护理机构的服务质量等同于最小化路径成本，因此所提出问题的特例等价于MDVRP。由于MDVRP是NP-hard［20］，故所提出的问题的特例也是NP-hard，即NP 难解问题。因此，所提出的MHHSP 问题具备NP 难解性。

2 本文算法

2.1 贪心算法

由于MHHSP 是一个NP 难解问题，获取最优解的时间会随求解问题的规模呈现指数级增长。为了在家庭护理机构可接受的时间范围内得到一个可行且合理的解决方案，本文首先针对MHHSP 提出一个贪心算法来快速生成一个可行的初始解。该算法的基本思想是在每个工作日期内，对老人集合按照开始等待服务时间进行升序排序，然后依次遍历所有老人，优先为开始等待服务时间较早的老人分配空闲且服务质量最高的护工。

贪心算法的求解步骤如下所示：

步骤1从D中选择一天d作为待分配日期，设置护工i在工作日d的护理路径Xid为空，以及该护工在第d天的最早工作时间为护工的上班时间，如算法1 第3 行所示。然后根据老人j的开始等待服务时间，对老人集合进行升序排序，并将排序后的老人添加到队列R中，如算法1 第2 行～第5 行所示。

算法1贪心算法

步骤2从R中选择开始等待服务时间最早的老人j。计算不服务老人j时所得到的整体服务质量为H。遍历所有护工，计算不同护工为老人服务时的整体服务质量H，并从中选择使整体服务质量最大且满足式（7）～式（9）的护工i服务老人j。最后，将老人j添加到路径Xid中。如算法1 第7 行～第22 行所示。重复步骤2，直至遍历完R。

步骤3重复步骤1 和步骤2，直至遍历完D。贪心算法的伪代码描述如算法1 所示。

定理2本文提出的贪心算法时间复杂度为O(gba+gb×logab)。

证明如算法1 所示，算法的整体结构主要包括3 个嵌套的for 循环。外层循环的次数为工作日期数目g，时间复杂度为O(g)；中间层循环的次数为老人数目b，时间复杂度为O(b)；当遍历每个老人时，内层循环需要遍历所有护工并计算服务质量，其循环次数为护工数目a，时间复杂度为O(a)，因此3 个嵌套的for 循环的时间复杂度为O(gba)；在为老人安排护工前，根据老人的服务时间进行快速排序，排序的个数为老人数目b，按照排序的结果从小到大遍历每一个老人，时间复杂度为O(b×logab)。快速排序与中间层循环同级，即整个算法的时间复杂度O(gba)+O(g) ×O(b×logab)=O(gba+gb×logab),因此贪心算法的时间复杂度为O(gba+gb×logab)。

为方便理解，本文通过一个例子来描述该算法的贪心策略。假设需要安排2 名护工（即k1和k2）为4 名老人（即p1、p2、p3和p4）提供服务，并且护工k1和k2均满足老人p1、p2、p3和p4的服务技能需求、服务时间、服务价格和服务人员约束。贪心算法首先根据老人开始等待服务的时间从早到晚对老人进行排序。假设排序结果为p1、p2、p3和p4，则该算法将进行4 轮调度，每轮调度选择一位护工服务一位老人。具体地，在第1 轮调度时，优先为老人p1安排服务。该算法遍历所有护工，并从中选择满足要求且使服务质量最高的护工（假设该护工为k1）为p1提供服务，同时更新护工k1的工作时间。第2 轮调度则为老人p2安排服务，重新遍历所有护工，并从中选择满足服务要求且使得服务质量最高的护工（假设为k2）为p2提供服务。经过4 轮调度后，得出k1的护理路径为的护理路径为

2.2 定制遗传算法

本文在贪心算法的基础上提出一个定制的遗传算法，对所生成的初始解作进一步优化。定制遗传算法中的每个解（个体）可由一条染色体表示，多个个体组成一个种群［21］。本文用一个二维数组表示一条染色体，其中第一维表示日期，第二维表示某一天所有护工的护理路径。图2 展示了染色体编码的一个示例，其中有5 名护工，40 名老人。在该例子中，本文将40 名老人编号为1～40，将5 名护工编号为41～45。由于一条护理路径由护工以及这名护工所服务的所有老人组成，因此，在染色体中，每条护理路径以护工的编号进行分隔，即2 名护工之间的编号代表前一名护工的护理路径。例如，路径1 包括编号为41 的护工、编号为1、5、23 的老人，即编号为41 的护工在周一依次服务编号为1、5、23 的老人。

图2 染色体编码Fig.2 Encoding of chromosome

本文定制的遗传算法基本思路是模拟自然界的优胜劣汰过程，目的是选出其中最好的个体［22］。本文首先将贪心算法生成的初始解作为定制的遗传算法初始种群，并对其进行编码；然后进行交叉、变异、选择操作得出下一代的种群，并循环上述步骤；最后，当迭代次数达到指定值时，终止循环并输出迭代过程中所能找到适应度最高的个体作为算法的解。

在本文遗传算法中，计算每个个体的适应度等价于计算该个体所对应解的服务质量，选择操作将根据个体的适应度来选择下一代的种群个体，适应度越高的个体被选择作为下一代种群的概率越高。

本文定制的遗传算法中各个算子的具体操作过程如下。

1）交叉

交叉是指交换2 个不同染色体（个体）中的某个片段（护理路径），从而产生新个体遗传到下一代。本文定制的遗传算法采用单点交叉方式，染色体之间有一定概率发生配对交叉。配对的2 个不同的个体一般从种群中随机选择，交换的片段从2 个染色体的同一行（同一天）随机选择。具体操作如图3 所示：从群体中随机选择染色体1 作为父亲，染色体2作为母亲，并随机选择1 名护工作为分隔点，将父亲染色体在分隔点前的片段以及母亲染色体在分隔点后的片段交换位置，形成2 个新个体。

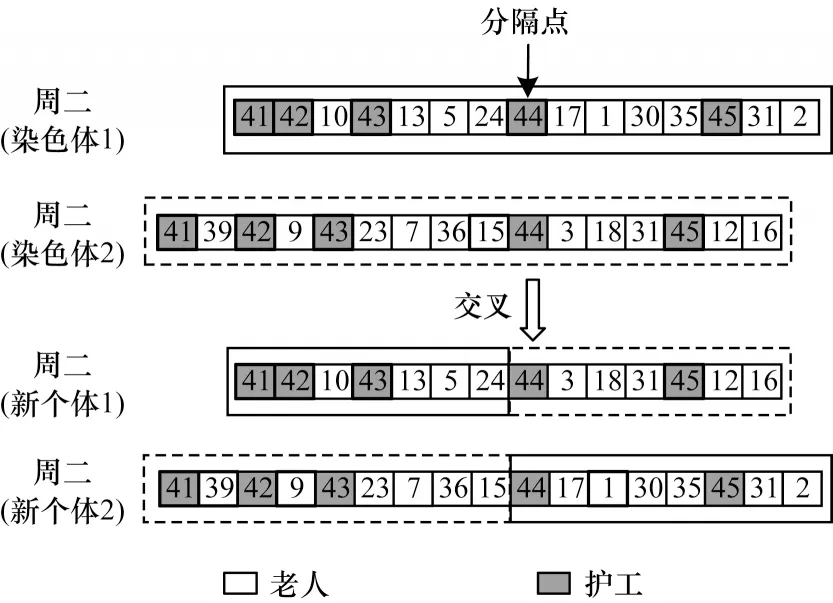
图3 交叉示例Fig.3 Example of crossover

2）变异

变异主要由插入、交换和删除3 种操作组成，每次迭代染色体均会随机选择3 种变异操作中的一种，发生一定概率的变异，产生新个体。具体地，插入操作是对于某一行中未出现（即未被服务）的老人，随机选择其中1 名，并将其插入到该行的随机位置中。删除操作是从染色体的某一行中随机选择1 个老人，并将其删除。交换操作是在染色体的某一行中随机选择2 个不同的老人进行位置交换。

图4 以某条染色体为例，展示了3 种变异。插入操作、删除操作和交换操作分别用符号+、−和X 来表示，（+，2，3，4）表示选择编号为3 的老人，将其插入到该染色体周二的护理路径中，插入的位置为4；（−，1，9）表示删除该染色体周一的护理路径中位置为9 的老人；（X，7，12，14）表示将该染色体周日的护理路径中位置为12 和14 的老人进行交换。

图4 变异示例Fig.4 Example of mutation

3 实验结果与分析

3.1 实验设置

本文在60 个实例的开源数据集［23］上进行实验，并以家庭护理机构的服务质量为指标与基准算法和随机算法进行比较。其中，基准算法由文献［18］基于MDVRP 提出，其贪心策略是优先为服务时长最长的老人安排能够提供服务质量最高的护工。该数据集由3 组不同规模（包括小规模、中规模和大规模）的实例组成，每组有20 个具体实例。其中，每个小规模实例均包含40 名待分配的老人和5 名空闲的护工，中规模例子包含80 名老人和10 名护工，大规模例子包含150 名老人和20 名护工。

本文模型的具体参数设置如表2所示。在定制的遗传算法参数配置中，设置种群迭代次数为100 次，种群大小设为500个，交叉和变异概率均设为0.2，变异的3种操作发生概率均为1/3。本文使用Python实现所提出的贪心算法和定制的遗传算法，在Windows 10、3.20 GHz Intel Core i7-8700 CPU 和16 GB 内存的环境上进行测试。

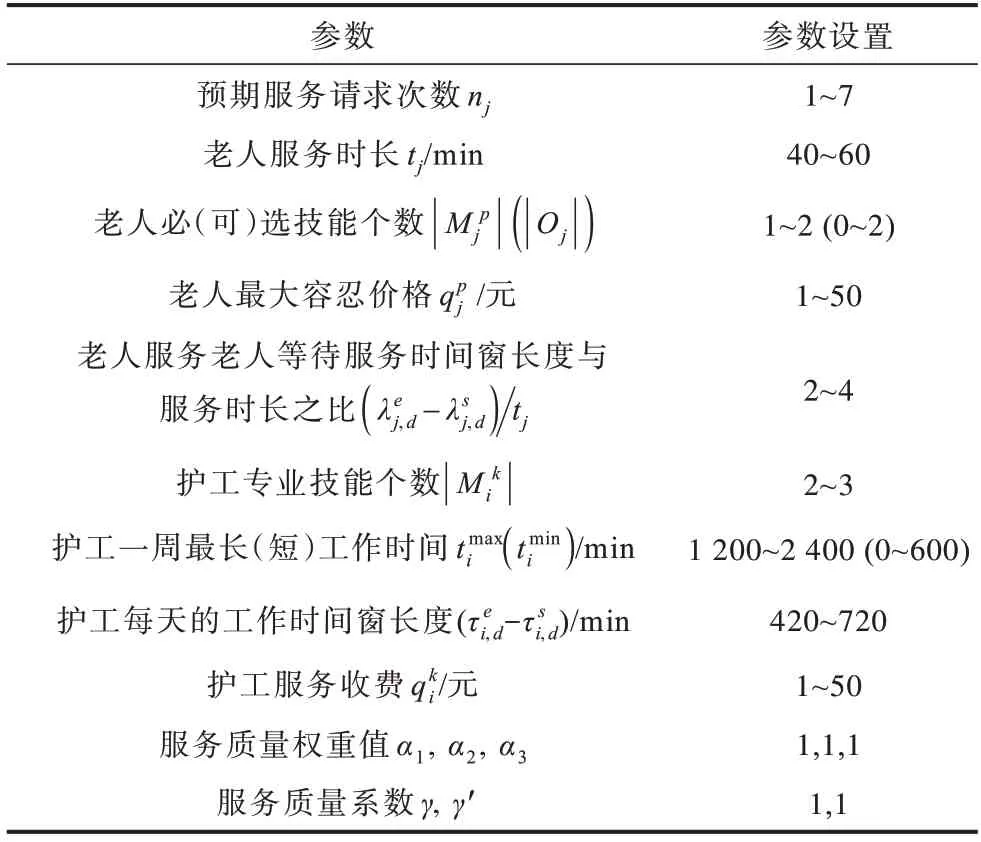
表2 参数设置Table 2 Parameters setting

3.2 结果分析

本文将贪心算法、定制的遗传算法与基准算法和随机算法在小、中、大这3 种规模的数据集中所得的结果进行对比，结果如图5～图7 所示。由图5 可知，对于小规模的数据集，贪心算法和定制的遗传算法所得到家庭护理机构的平均服务质量相较基准算法分别提高35.7%和89.7%，较随机算法分别提高51.1%和111.4%。由图6 可知，贪心算法和定制的遗传算法在中规模数据集上所得到的平均服务质量相较基准算法分别提高32.6%和94.5%，较随机算法分别提高81.9%和166.9%。由图7 可知，对于大规模的数据集，贪心算法和定制的遗传算法所得到的平均服务质量较基准算法分别提高30.4%和49.7%，较随机算法分别提高87.2%和114.9%。

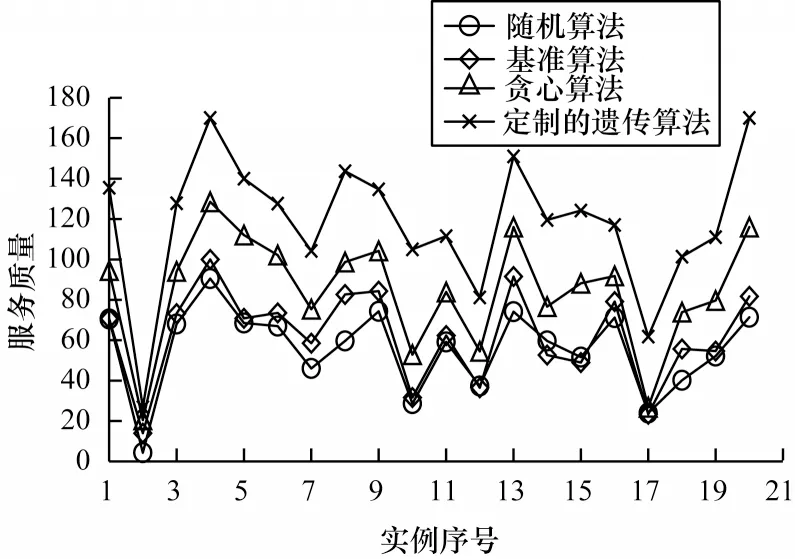
图5 不同算法在小规模数据集下的服务质量Fig.5 Service quality of different algorithms on small data set

图6 不同算法在中规模数据集下的服务质量Fig.6 Service quality of different algorithms on medium data set

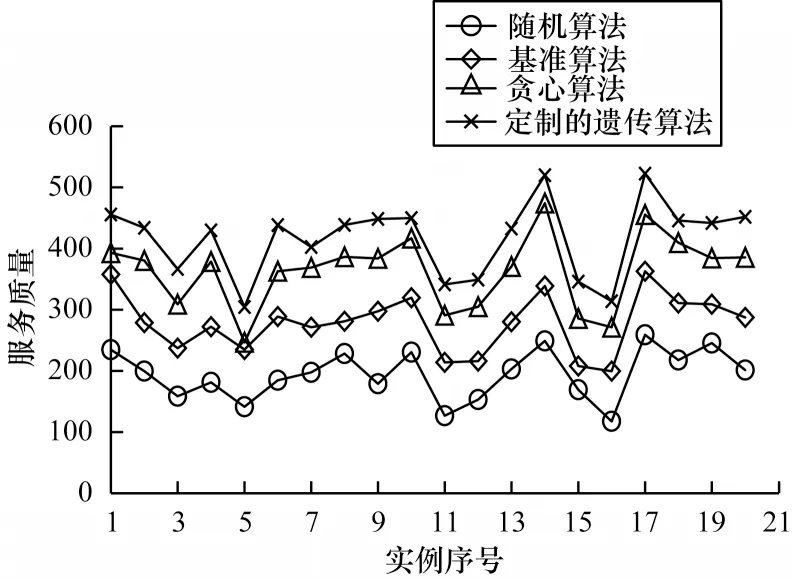
图7 不同算法在大规模数据集下的服务质量Fig.7 Service quality of different algorithms on large data set

在图5～图7 中，对于任意规模的任意例子，贪心算法和定制的遗传算法所得到的服务质量均比随机算法所得到的服务质量高。整体而言，相比于基准算法，贪心算法和定制的遗传算法的服务质量分别提高了31.7%和65.7%；相较于随机算法，贪心算法和定制的遗传算法的服务质量分别提高了79.8%和126.3%。这是因为在贪心算法中，老人按照开始等待服务时间升序排序，且服务时长较短的老人优先被服务，在护工有限的工作时间下，可以服务更多的老人，从而减少老人未被服务的次数，提高家庭护理机构的服务质量。定制的遗传算法以适应度为衡量标准在种群中淘汰部分适应度较差的个体，经过多轮迭代后，得到的个体一定比初始种群中个体的适应度更高。因此，贪心算法和定制的遗传算法所得到的护工路径使服务质量更高，比基准算法和随机算法的效果更好。

如图8 所示，以小规模数据集的实例1 为例，随着迭代次数的增加，观察家庭护理机构的服务质量变化。当迭代次数范围在0～84 时，服务质量的最优值和平均值显著增长。当迭代次数大于84 时，服务质量的最优值和平均值保持不变。实验结果表明，定制的遗传算法在第84 代左右得到的适应度基本稳定，并且能够在迭代次数为100 次内快速获得MHHSP 的较优解。

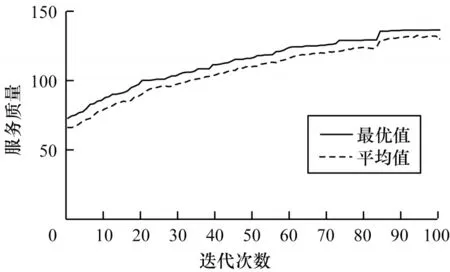
图8 定制的遗传算法每次迭代的服务质量Fig.8 Service quality of per iteration of customized genetic algorithm

表3 所示为不同算法在不同规模实例中从开始到结束的平均运行时间。由表3 可知，本文提出的遗传算法与贪心算法的平均运行时间比随机算法的运行时间长。从算法运行的循环次数来看，贪心算法需要一定时间对工作日期、老人集合以及护工集合进行3 层循环，而定制的遗传算法需要进行100 次迭代，因此所提出的贪心算法、定制的遗传算法和基准算法均比随机算法的运行时间长，且所提出的贪心算法和基准算法的运行时间较接近。其中：随机算法、贪心算法和定制的遗传算法在小规模数据集上的平均运行时间分别为0.005 s、0.050 s 和83.150 s，贪心算法与随机算法的运行时间比较接近，均小于1 s。

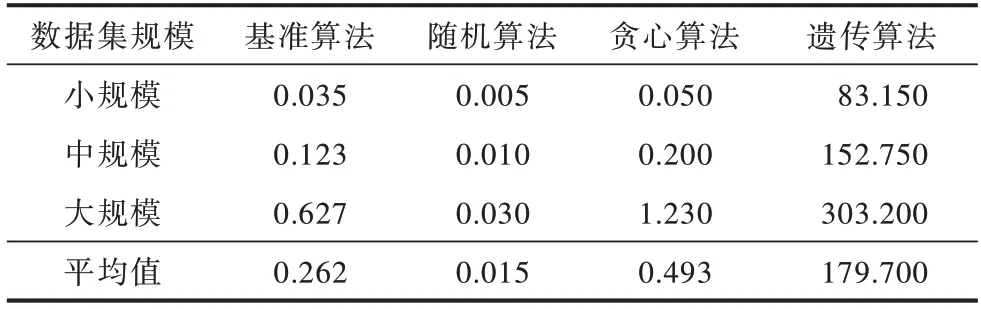
表3 不同算法在不同规模数据集下的运行时间Table 3 Average running time of different algorithms on different scale data sets s

图9 为在不同算法所得到的解中，不同服务次数的老人数量分布情况。其中，横坐标的“0”表示老人一周内没有被服务，“1”表示老人一周内被服务一次，以此类推。由图9 可知，当服务次数范围在0～2时，随着老人服务次数的增加，老人的数量也在增长；当服务次数大于2 时，老人的数量随之减少，这是因为大多数老人的申请服务次数为2 次左右。当服务次数大于2 时，贪心算法和定制的遗传算法的解所分配的老人比基准算法和随机算法高，贪心算法和定制的遗传算法可以提高老人一周内被服务的次数。

图9 服务次数的分布情况Fig.9 Distribution of service times

4 结束语

本文将多周期家庭护理路径规划与调度问题归约为多车场车辆路径优化问题，证明其NP 难解性。同时利用贪心算法为服务开始时间早的老人优先安排服务质量最高的护工，并将得到的结果作为初始解，通过定制的遗传算法得到更优的可行解。实验结果表明，相较于基准算法和随机算法，本文贪心算法和定制的遗传算法可有效提高服务质量。由于老人的服务需求存在不确定性，如新增1 个待服务老人、老人的服务时间改变、老人临时取消服务等均会对家庭护理的服务质量产生影响，因此下一步将考虑家庭护理中服务请求的动态性，设计一个在线的低复杂度近似算法对护工路径规划方案进行实时调整，从而完善本文算法。