巷道悬臂式掘进机控制平台模拟研究
李晓宙
(山西潞安工程有限公司, 山西 长治 046102)
引言
掘进机是一种移动设备且由许多子系统组成的机器,如图1 所示。刀盘驱动子系统由多台电机驱动如图2 所示,产生足够的扭矩进行挖掘。因此,它在硬岩掘进中起着重要的作用。虽然有许多研究人员对刀盘驱动系统控制进行了研究,但仍存在问题还有待解决。用于独立控制每个驱动电机,每个轴的控制器不接收任何信息从本质上来说,它是一个解耦控制器,设计时没有考虑刀盘驱动系统的整个动态模型。由于缺乏协调对于多电机驱动系统解耦控制器通常会导致性能下降。因此用于开发可实施且高性能的协调控制刀盘驱动系统控制器是十分必要的。
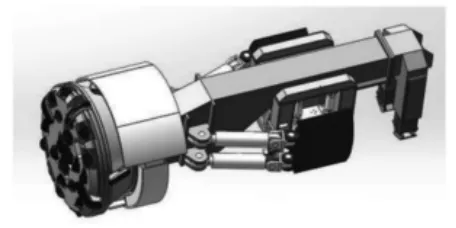
图1 硬岩隧道掘进机

图2 硬岩掘进机刀盘驱动系统
1 悬臂式掘进机控制平台模型建立
1.1 非线性刀盘驱动模型
刀盘驱动系统结构如图3 所示。TBM 刀盘驱动系统的工作原理[1]如下:
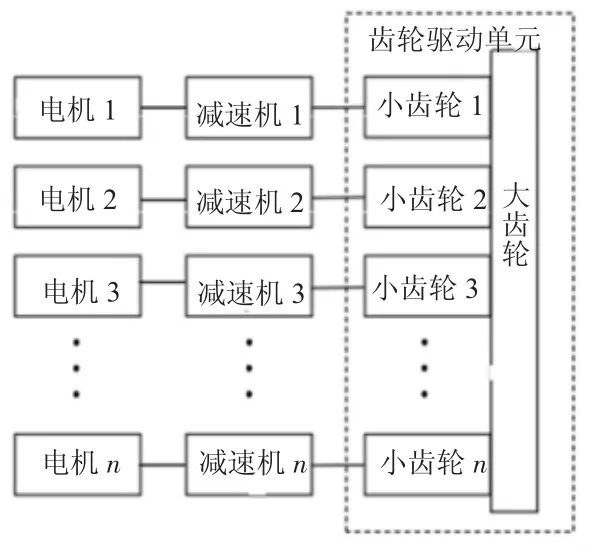
图3 硬岩隧道掘进机
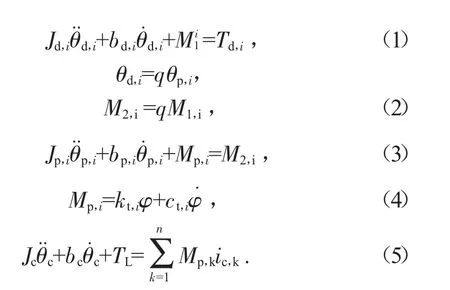
式中:Td,i为产生电动转矩Td,i=kiud,i.Jd,i为第i 个联轴器的惯性;bd,i为黏性阻尼比;θp,i为第i 个电机转子的角位移;q 为减速器比;θp,i为第i 个主动小齿轮的角位移;Jp,i为i 等效耦合后的主动小齿轮惯性;bp,i为第i 个等效耦合后的主动小齿轮阻尼比;θc为刀盘角位移;Jc为刀盘惯性;bc是刀盘黏性阻尼比;Mp,i为第i个小齿轮和大齿轮之间啮合扭矩;TL为总负载扭矩。齿轮啮合过程是一个非线性过程传动过程,啮合扭矩Mc的表达式[2]:
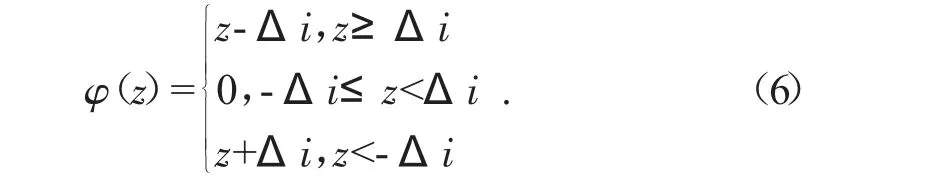
式中:z=θp,i-im,iθm-ei(t)/ri,Δi 为第i 个小齿轮的总齿轮齿隙;ei(t)为第i 个小齿轮传动误差;ri为第i 个主动小齿轮的半径。
1.2 简化动态模型
对于控制器设计,可以被视为理想的传输过程,因此方程[3]可以得到。

将式(7)代入式(3),可以得到刀盘驱动系统的二阶动力学模型[4]。
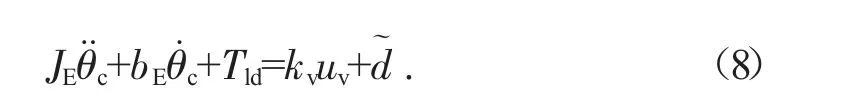
θ˙可以定义为vc和vd,将速度误差定义为e=vc-vd,所以系统动力学可以重写为:
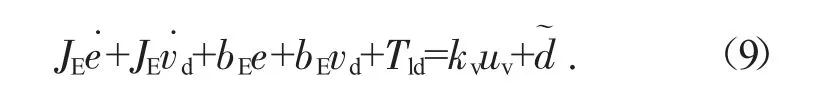
假设1 参数不确定性的程度和已知不确定非线性,即:
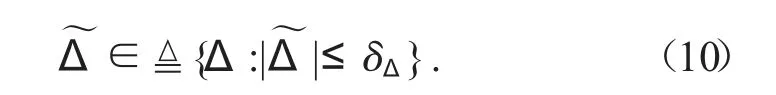
式 中:θmin=[θ1min,θ2min,θ3min]T,θmax=[θ1max,θ2max,θ3max]T和δΔ已知。
2 控制算法
2.1 不连续投影

式中:Γ>0 是对角矩阵;τ 是自适应函数,待以后合成。投影映射projθ^(·)=[projθ^(·1),…,projθ^(·3)]
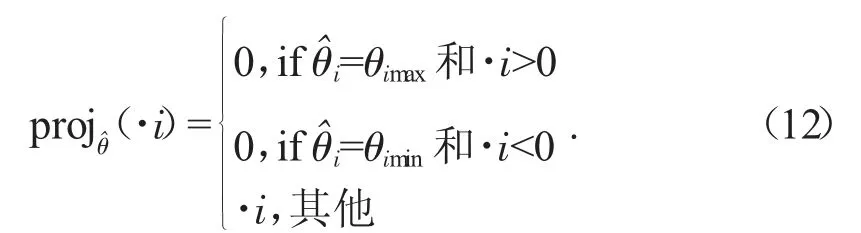
可以证明,对于任何自适应函数τ,式(12)中使用的投影映射[5]保证了以下几点:
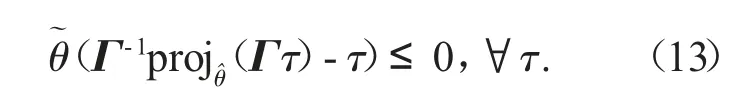
2.2 自适应鲁棒控制律
定义一个半正定函数
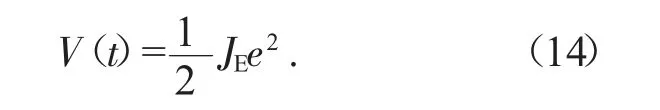
分化与产量
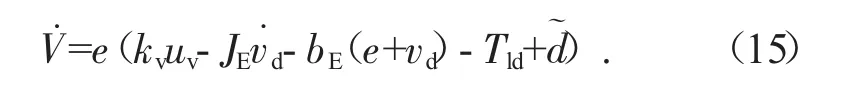
此外,式(9)中的项可以线性参数化为
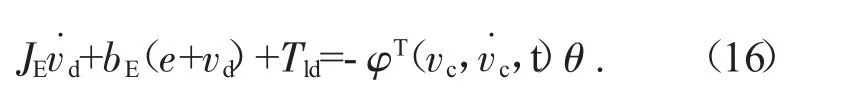
τ∈R3×1是已知函数的矩阵,称为回归者。然后,等式(15)可以改写为
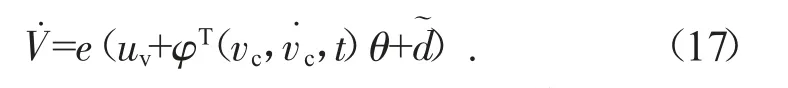
注意到式(16)的结构,提出了以下定律:
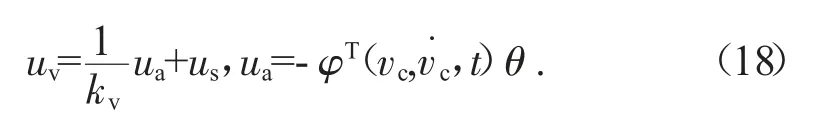
式中:ua是可调模型补偿,us是一种鲁棒控制律以后再合成。将式(18)替换为式(17),结果如下:可以获得表达式。
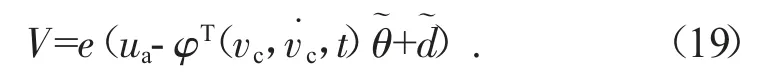
鲁棒控制律由两项组成:
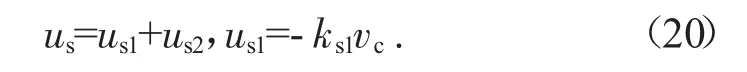
式中:us1用于稳定标称系统,即选择为简单的比例反馈,ks1为半正定函数值,而us2是用于衰减影响的反馈保证鲁棒性能的模型不确定性分析。注意假设1,存在us2,因此满足以下两个条件:
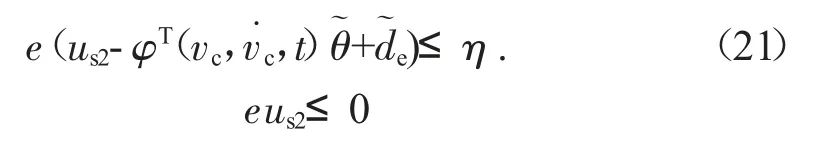
式中:η 是一个可以任意小的设计参数。满足(21)的us2的一个光滑示例被给出为其中h 是满足h 的任何光滑函数和θM=θmax-θmin。
2.3 控制分配
刀盘驱动系统装配产生的力错误、作用于每个电机轴的干扰以及齿隙非线性可能导致驱动扭矩不平衡。为了更好地实现驱动扭矩分配,条件可以满足写为:
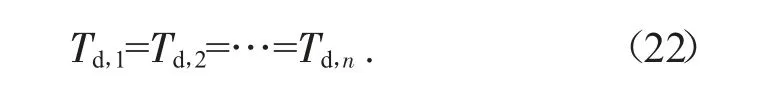
驱动扭矩可以适当地写为Td,i=kiui,可获得控制输入。

转矩常数ki是影响控制分配的唯一因素,控制策略不仅可以实现良好的运动,而且可以提高运动速度导致良好的驱动扭矩协调。
3 模拟参数及结果
3.1 模拟设置
仿真控制器以验证有效性,系统参数如表1所示。
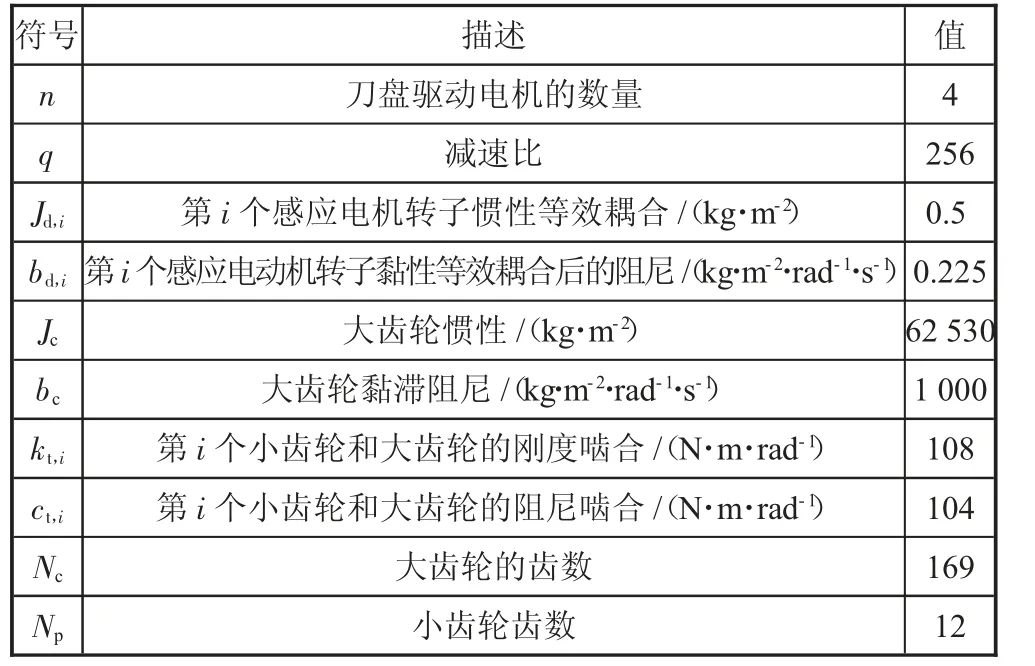
表1 模拟参数
3.2 模拟结果
为了验证所提出的控制器的性能,比较了以下控制算法。
算法1(C1)控制参数设置为kp、ki和kd。对于每个驱动电机,正确选择控制器增益,当kp=60,kd=0,ki=1528 时,由此产生的闭环传递函数有一对主极点在-50。
算法2(C2)us2=ks2(q)e,其中ks2(q)是非线性比例反馈增益。需要足够大的恒定反馈增益ks1用于简化生成的控制律。选择us=-ks1e,其中ks1表示组合增益us1和us2,控制器参数选择为ks1=485,适应率设置为Γ=diag[1,0.1,12228]。选择参数后,将生成闭环传输函数有一对主极点-50 与C2 相同,执行以下测试集。
第1 组:各电机的参数驱动假设装置相同,不考虑扰动TL。
第2 组:增加一个干扰TL来测试性能每个控制器对干扰的鲁棒性。
第3 组:齿隙非线性Δi 齿轮啮合过程中也用于测试每个控制器的扭矩分配性能。
第4 组:齿隙非线性Δi 和TL都被考虑用于测试发动机的扭矩分配性能。
当干扰TL添加到刀盘时进行测试结果如图4、图5 和图6 所示。发现不仅性能相似,作用在刀盘上的扰动对驱动扭矩的影响也很小。
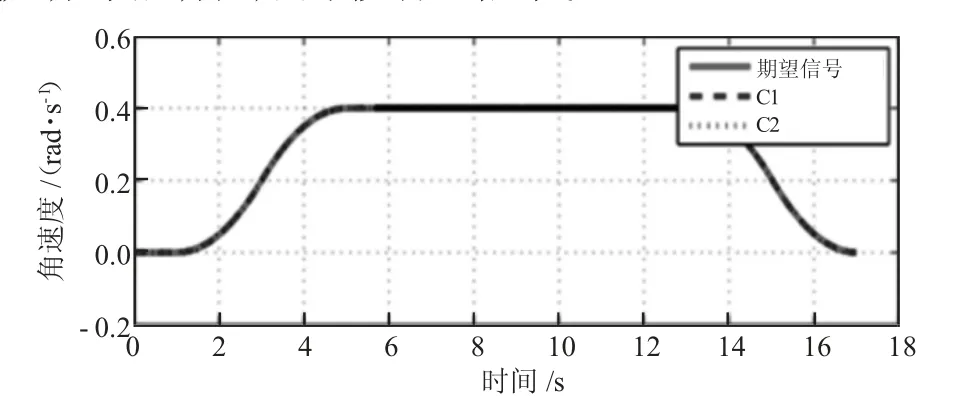
图4 2 组的比较控制性能
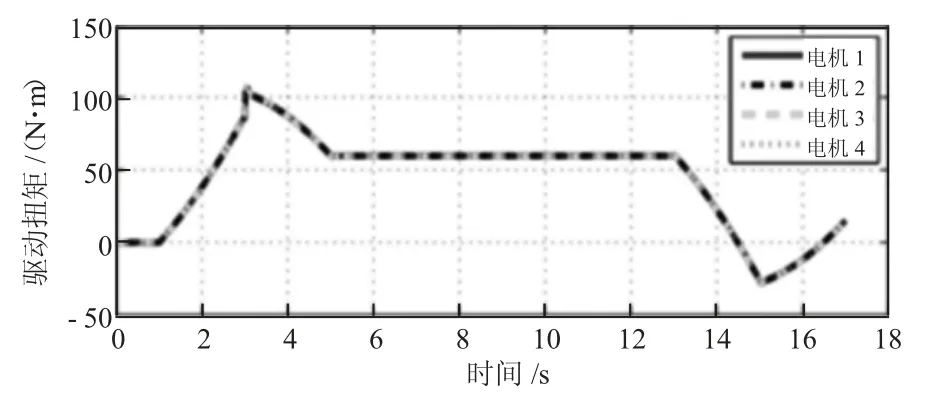
图5 2 组的C1 控制输入
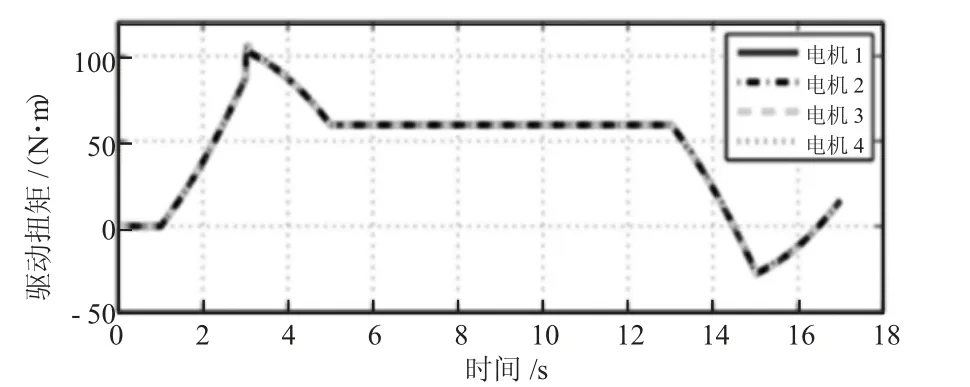
图6 2 组的C2 控制输入
从模拟结果图7 可以看出速度跟踪性能也可以很好地实现C1 和C2。虽然齿隙非线性不存在对跟踪性能有显著的负面影响,但是它对驱动力矩的影响对于控制器来说是不可忽视的。然而,驱动扭矩不会变得不均匀。此外,实际情况比所给出的模拟严重得多,因此它结合了1 组和2 组中的影响因素。从仿真结果如图10、图11 和图12 所示,验证了该控制器的优越性能。自从考虑了齿隙和扰动TL的影响,电机驱动扭矩将变得非常不同用于控制器C1。所有结果证明所提出的控制器不仅可以实现良好的跟踪性能,但也能分配驱动扭矩均匀。
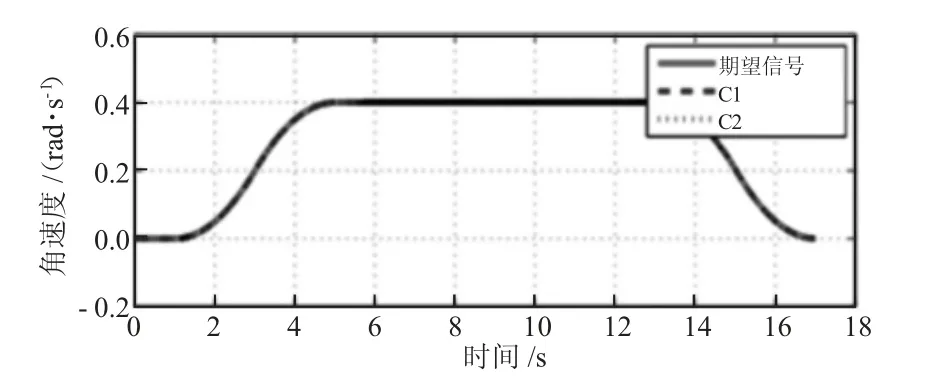
图7 3 组的比较控制性能
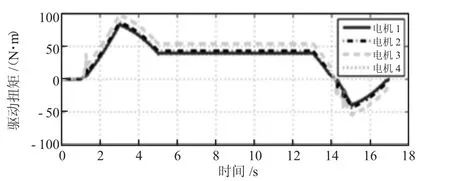
图8 3 组的C1 的控制输入
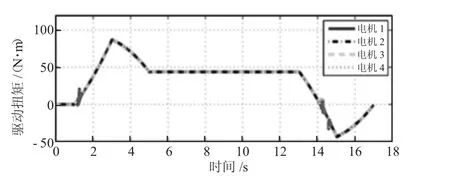
图9 3 组的C2 控制输入
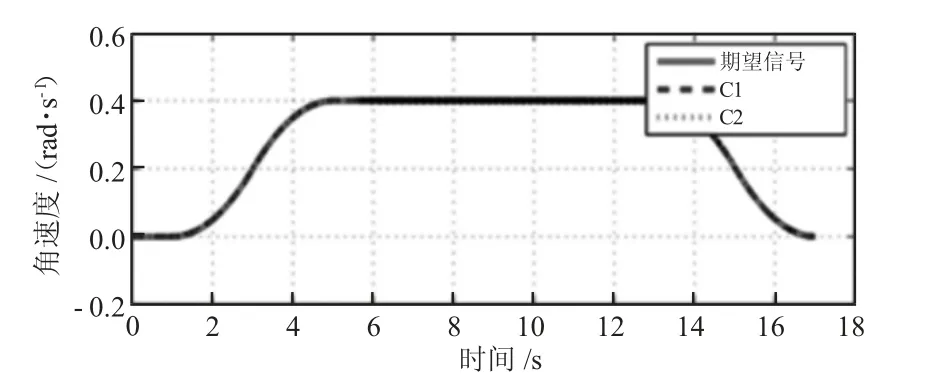
图10 4 组的比较控制性能
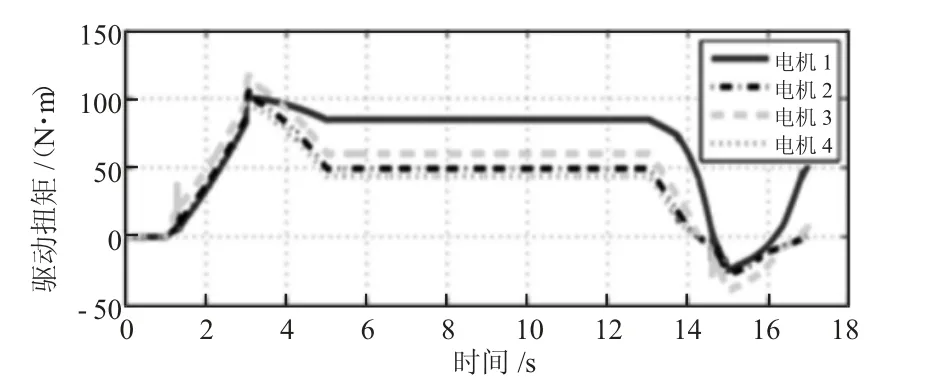
图11 4 组中C1 的控制输入
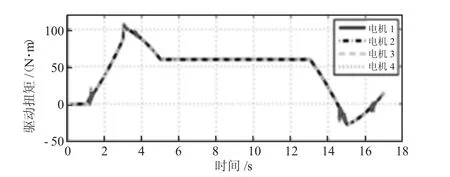
图12 4 组的C2 控制输入
4 结语
本文研究了驱动巷道掘进机刀盘驱动系统的同步控制问题。建立了多电机驱动系统的广义非线性时变动力学模型,其中还考虑了齿隙非线性。针对驱动刀盘驱动系统,提出了一种结合控制分配的自适应鲁棒控制律,提出了一种实现良好跟踪性能的方法通过主动调节驱动扭矩实现同步运动每台电机的驱动力。结果表明,所提出的控制器在理论上保证了在指定分配情况下性能。比较仿真结果表明,该方法具在存在齿隙非线性和干扰的情况下有良好的性能。

