Agent信念修正推理机制
林 颖,郝一江
(1.宁德师范学院 马克思主义学院, 福建 宁德 352100;2.中国社会科学院 哲学研究所, 北京 100732)
一、引言
Agent(主体或智能体)是人类智能、动物智能和机器智能的统一模型(1)参见张晓君、郝一江所著《基于行动逻辑的智能主体行为表征研究》,原载于参考文献[1],后被人大复印资料《逻辑》2013年第2期全文转载。。行动或行为(包括言语行为)可以改变世界,进而改变主体的信念、愿望、意图和情感等心智态度,简言之:行动改变心智。每当某个可靠的新信息与主体已经拥有的信息相矛盾时,如果主体想整合这一新信息,并保持其信念集一致,主体就必须改变其信念(belief),这时就会执行信念更新行动。Agent常见的三种信念更新行动是:信念扩展(expansion)、信念收缩(contraction)和信念修正(revision)。信念扩展会导致某个公式被相信;信念收缩会导致某个公式不再被相信;信念修正会导致之前被相信的公式不再被相信。本文试图用形式化的方法表征这三种动态信念更新行动。
基于意图的主体结构在人工智能和系统工程等领域有着广泛的应用。意图系统描述的实体行动可以通过归因于某些心智态度的方法来预测,这些心智态度包括知识、信念、愿望、意图、义务和承诺等[2]。最为著名的意图形式化系统是Rao与Georgeff[3]提出的信念、愿望和意图(Belief-Desire-Intention,简称BDI)逻辑。信念用来表示环境状态,愿望用来表示主体动机,意图用来表示主体目的。BDI体系结构随着时间的推移而不断发展,并已应用于迄今为止开发的几个最重要的多主体系统中。
国内外关于信念、愿望和意图等心智状态与Agent行动之间的关系的文献较为丰硕。例如: Bratman等[4]、Gärdenfors[5]、Casali等[6]、 林颖等[7-8]、张晓君[9]等。本文将在Meyer等[10]、Linder等[11]成果的基础上,利用命题动态逻辑,对主体的动态信念更新行动的推理机制进行形式化的表征,其基本思路是:(1)定义“执行信念更新行动的结果事件状态”;(2)定义“为使主体有机会执行信念更新行动所需要满足的条件”;(3)定义“主体为了能够执行信念更新行动需要具备的能力”;(4)在定义信念收缩行动的结果时,引入选择函数的概念,这些函数可以选择状态集的子集,并将其添加到主体的信念选项集中,从而收缩主体的信念集;(5)信念修正被定义为:信念收缩行动和信念扩展行动的序列组合行动;(6)根据主体的知识和信念可以定义主体采取信念更新行动的能力。这些定义是基于这样的理念:即执行能行行动可以得到主体所意图的事件状态。通过证明Gärdenfors信念更新公设的有效性,可以证明这些信念更新行动的定义是直觉上可接受的、合理的[11]103-104。
二、知识、信念、能力、机会及其结果
在表示知识和信念时,遵循认知和信念逻辑的通用方法,从句法和语义双重视角来加以表征。公式Kiφ表示主体 i知道φ,公式Biφ表示主体i相信φ。在语义方面,采用克里普克式的可能世界模型。
执行行动的结果被定义为“行动的执行所导致的事件状态”[12]。表征行动就需要弄清执行行动能力与执行行动的机会之间的关系。命题动态逻辑[13]不仅可以很好地对这些概念进行形式化,而且在语义方面还可以使得认知逻辑和动态逻辑兼容:因为可能世界语义可同时给出认知概念和动态概念的意义[11]104-105。
在本文中,主体的能力通过Ai算子加以形式化,公式Aiα表示主体 i有能力执行行动α;事件doi(α)表示主体i执行行动α后的表现;〈doi(α)〉φ表示主体i有机会执行α,而且执行α后会导致公式φ成立;公式[doi(α)]φ表示:只有当主体i的事件状态满足公式φ时,机会才会出现。现在给出主体执行行动所导致的信念更新的语义框架,其中p表示命题变元,a表示原子行动,α表示行动,φ和ψ表示公式。由于每个状态对应于一个可能世界,所以,本文对状态和可能世界不加区分,都用w表示。
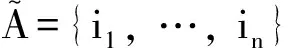
(1)L是Δ的最小超集(superset),并且满足:
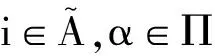
(2)Π0是Π的最小超集,并且满足:
① 如果φ∈L,那么confirm φ∈Π;
② 如果α1∈Π且α2∈Π,那么α1; α2∈Π;
③ 如果φ∈L且α1, α2∈Π,那么if φ then α1else α2fi∈Π;
④ 如果φ∈L且α1∈Π,那么while φ do α1od∈Π。
注记:语言L的纯粹命题片段记为L0。逻辑符号∧, →,↔, tt, ff, Miφ与[doi(α)]φ的定义与往常一样。其他附加结构可以是由定义缩写引入:skip表示confirm tt,fail表示confirm ff,α0表示skip,αn+1表示(α;αn)。执行confirm φ就是确认φ成立,α1; α2∈Π是序列组合行动,if φ then α1else α2fi∈Π是条件组合行动,while φ do α1od∈Π是重复组合行动。skip表示空行动,fail表示从未成功的行动。
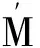
(1) W是一个可能世界或状态的集合。
(2) f:Δ×W→{0, 1}是一个全函数,为可能世界中的命题变元指派真值。
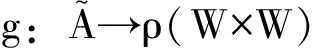
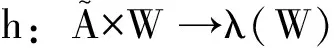
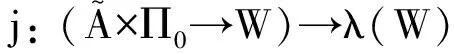
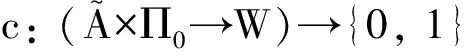
定义2在定义可及关系生成函数g和信念选项集生成函数h时,分别使用了满足S5公理的知识概念和满足K45公理的信念概念。
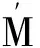
其中状态转换函数j和能力函数c定义如下:
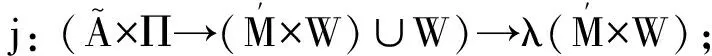
② j(i, a)(M, w)=M, j(i, a)(w);
③ j(i, confirm φ)(M, w) = {(M, w)},当M, wφ时;
= ∅,否则;
④ j(i, α1; α2)(M, w) = j(i, α2)(j(i, α1)(M, w));
⑤ j(i, if φ then α1else α2fi)(M, w) = j(i, α1)(M, w),当M, wφ时;
=j(i, α2)(M, w),否则;
⑥ j(i, while φ do α1od)(M, w)= {(M′, w′)|∃k∈N∃M0, w0… ∃Mt, ws
[M0, w0=M, w & Mt, wt=M′, w′& ∀s [Ms+1, ws+1=j(i, confirm φ; α1)(Ms, ws)]& M′, w′φ]} 其中s和t是自然数,j(i, ∅)=∅且: 2) c(i, a)(M, w) = c(i, a)(w) 3) c(i, confirm φ)(M, w) = 1,当M, wφ时; = 0,否则; 4) c(i, α1; α2)(M, w) = c(i, α1)(M, w) ( c(i, α2)(r(i, α1)(M, w)) 5) c(i, if φ then α1else α1fi)(M, w) = c(i, confirm φ; α1)(M, w)或 6) c(i, while φ do α1od)(M, w) = 1,当∃t∈N[c(i, (confirm φ; α1)t; = 0,否则。 其中N是自然数集, c(i, α)(∅)= 1。 可满足性和有效性定义与往常一样。其中,c(i, confirm φ)(w)表示:一个主体i能够确认公式φ,当且仅当,公式φ成立。j(i, confirm φ)与c(i, confirm φ)蕴含了:在φ成立的环境下,主体i既有机会又有能力确认φ。一个主体有能力执行一个序列组合行动α1; α2,当且仅当:主体有能力执行α1,且在它执行完α1之后有能力执行α2。一个主体有能力执行一个条件组合行动,其意思是:或者主体能够确认该条件,然后执行then之后的行动;或者它能够确认该条件的否定命题,然后执行else之后的行动。一个主体有能力执行一个重复组合行动while φ do α1od,当且仅当:对于某个t∈N,主体能够执行行动(confirm φ ; α1)t; confirmφ[11]107-108。 本文所采用的知识与信念概念的区别与往常一样[14],即信念不满足D公理(Biφ∧Biφ),而且假设存在不一致的信念集,信念扩展可能导致主体有不一致或者荒谬的信念。 通过执行信念更新行动,主体可以扩展、收缩和修正其信念。这些信念更新行动受到主体知识边界集(boundary set)的影响,即,在一个给定模型状态下可以确定知识的范围,并假定知识不会因为信念更新行动而改变,这样,知识被看作是笃定的信念[11]110-111。 从句法的角度来看,使用3个新的信念更新行动可以对行动集Π加以扩展。 定义4:对定义1的行动集Π(进而语言L)可以进行如下扩展: 如果φ∈L0,那么expand φ, contract φ, revise φ∈Π。 在一个模型的状态下的命题公式的真值,仅仅取决于对该状态的赋值。 命题1:令M=〈W, f, g, h, j, c〉是某个克里普克模型,且w∈W,令M′=〈W′, f′, g′, h′, j′, c′〉是某个克里普克模型,且w′∈W′,那么以下结论成立: ∀p∈Δ[f(p, w)=f′(p, w′)]⟹∀ψ∈L0[M, wψ⟺M′, w′ψ] 施归纳于ψ的结构即可证明命题1,详细证明可以参见Linder等[11]128。 信念扩展是一种行动,执行该行动可以导致进入“某个公式被相信的”事件状态。对主体的信念集的扩展建模,是通过限制主体的信念选项集来完成的。在模型M的世界w中,如果某个主体 i用公式φ对信念进行了扩展,那么主体i将限制其信念选项集满足φ。 信念扩展具有如下性质: 命题2:对于所有主体 i以及所有命题公式φ, ψ,有: 证明可以参见Linder等[11]128。式(1)表示用某个公式φ对信念进行扩展后的结果就是主体相信该公式α。式(2)表示用某个公式ψ对信念进行扩展后,主体将一直相信该公式ψ。式(3)表示在主体已经相信某个公式的情况下,再用该公式对主体信念进行扩展,不会改变任何结果。 信念扩展行动具有可实现性、确定性和幂等性。可实现性是指在任何情况下,主体都有机会执行行动。确定性是指执行行动导致的事件状态是唯一的。幂等性是指执行行动两次或任意多次,与执行一次的效果是一样的[11]111-112。 命题3(信念扩展的性质):对于所有的主体 i以及所有命题公式φ和ψ,有:[doi(expand φ)]Biψ↔( Bi(φ→ψ)。 证明可以参见Linder等[11]129-130。命题3表示用某个命题公式φ对信念进行扩展后,主体相信ψ,当且仅当,在进行信念扩展之前,主体就相信φ蕴涵ψ。可以证明命题3的如下特例:用某个公式对主体进行信念扩展后,导致主体具有荒谬的信念,当且仅当,在进行信念扩展之前,主体就相信该公式的否定,即: 推论1:对于所有的主体 i以及所有命题公式φ和ψ,有: 证明:根据观察可以发现:φ和φ→ff是等价公式,再结合命题3即可得证。证毕。 信念收缩通常是指一些之前被相信的公式在之后就不再被相信了。主体相信的内容由于信念收缩而变成了怀疑。为了至少包含“一个不满足被收缩的公式的状态”,就需要对主体的信念选项集进行扩展。为此,需要引入选择函数,尽可能以合理的且直觉上可接受的方式,来选择认知选项集的子集,从而达到信念收缩行动的目的。 ∑0:σ(i, w, φ)=σ(i, w′, φ),其中w′∈[w]g(i); ∑5:σ(i, w, φ∧ψ)⊆σ(i, w, φ)∪σ(i, w, ψ); 这一信念收缩行动的定义基于选择函数的使用,即通过把选择函数所选择的世界精确地添加到主体的信念选项集,从而完成信念收缩行动。 定义7(收缩行动的语义):令某个模型M=〈W, f, g, h, j, c〉,w∈W,且给定主体i和命题公式φ,并令σ是对于M的任意且固定的选择函数,可以定义:j(i, contract φ)(M, w)=M′, w,其中M′=〈W, f, g, h′, j, c〉且: (1) 如果i′≠i或w′∉[w]g(i),那么h′(i′, w′)=h(i′, w′); (2) 对于所有w′∈[w]g(i), h((i, w′)=h(i, w′)∪σ(i, w, φ)。 使用选择函数定义收缩行动的语义,可得到如下可接受的形式化信念收缩行动: 命题4:对于所有主体 i,命题公式φ, ψ和θ,有: 其证明请参见Linder等[11]130-131。式(1)表明信念收缩后的信念集包含在收缩前的信念集中。式(2)表明在φ不被相信的情况下,信念收缩φ不会改变什么。式(3)表明带有可收缩公式的信念收缩的结果是:将导致主体不再相信该收缩公式,而且可收缩公式是主体愿意放弃相信的公式。式(4)表明在用一个公式进行信念收缩,然后用该公式进行信念扩展时,将恢复初始信念集中的所有信念。式(5)表明用等价的公式进行信念收缩,会得到相同的信念集。式(6)表明先用φ进行信念收缩,然后用ψ进行信念收缩后,那么被相信的所有公式等价于:同时用φ∧ψ进行信念收缩后被相信的所有公式。式(7)表明如果用φ∧ψ进行信念收缩导致φ不被相信,那么为了收缩而被移除的公式,不会多于为了收缩φ∧ψ而被移除的公式[11]115-116。 与信念扩展一样,信念收缩具有可实现性、确定性和幂等性,即: 命题5:对于所有主体 i和命题公式φ, ψ,有: 证明:根据定义7即可得证。证毕。 选择函数可以是给定模型的信念集的某些极大子集。因为:假设M是带有状态w的某个克里普克模型,给定某个主体 i,并且假设对于某个命题公式φ,M, wBiφ∧Kiφ。在模型M中,把[w]g(i)∩φ中的世界添加到主体i的信念选项集,可得到“主体不再相信φ”的一个模型。 选择函数的目标是得到“给定公式失效”的一组世界。选择函数仅仅从认知等价类中添加所有可能世界,而这些世界不支持被收缩的公式,即使这些世界之前相信该公式。如果之前不相信该公式,就不必添加新的可能世界。信念收缩行动实施后的信念状态也可以用主体的知识和信念来描述[11]120-121。 信念修正是一种信念改变,即某个公式的信念状态被颠覆,即:主体之前相信φ,信念修正的结果是主体相信φ;或者主体之前相信φ,信念修正的结果是主体相信φ。信念修正可以用信念收缩和信念扩展来定义,使用某个公式φ的信念修正相当于用φ进行信念收缩之后,再用φ进行信念扩展[15]。行动集Π在序列组合下是封闭的,因此可以把信念修正定义为:信念收缩行动和信念扩展行动的序列组合行动。 定义8(信念修正):令某个模型M=〈W, f, g, h, j, c〉,w∈W,给定某个主体i和命题公式φ,可以定义:j(i, revise φ)(M, w) = j(i, contractφ; expand φ)(M, w)。 命题6:对于所有主体 i,所有命题公式φ, ψ, θ,有: 其证明请参见Linder等[11]138。式(1)表明主体相信φ是用φ修正其信念而得到的结果。式(2)表明用φ进行信念修正后得到的信念集,包含在用φ进行信念扩展而得到的信念集中;即用φ进行信念修正,就是用一致的方式得到包含φ的信念集,这一信念集是“直接用φ进行信念扩展而得到的信念集”的子集。式(3)表明信念扩展是一种特殊的信念修正:在φ不被相信的情况下,用φ进行信念扩展和用φ进行信念修正,实际上是相同的行动。式(4)从左到右方向的蕴涵表明:如果主体相信φ,即,φ是主体永远坚信的一个公式,那么用φ进行信念修正会得到荒谬的信念集,即,主体相信ff是用φ进行信念修正的结果;式(4)从右到左方向的蕴涵表明:荒谬的信念集只有在使用不可修正的公式进行修正时才会产生。式(5)表明用主体已经相信的公式进行信念修正,其结果不变。式(6)表明:用合取式φ∧ψ进行信念修正得到的信念集,是“用φ进行信念修正再用ψ进行信念扩展而得到的信念集”的子集。式(7)表明:如果用φ进行信念修正并不导致ψ被相信,那么用φ∧ψ进行修正得到的信念集,就是“用φ进行信念修正再用ψ进行信念扩展而得到的信念集”的一个超集。式(6)和式(7)给出的是信念修正的最小更新条件[11]121-122。 与信念扩展和信念收缩一样,信念修正具有可实现性、确定性和幂等性,即: 命题7:对于所有主体 i,所有命题公式φ, ψ,有: 证明:根据定义8即可得证。证毕。 命题8(信念修正的特征):对于所有主体 i,所有命题公式φ和ψ,有: (3) 如果信念收缩行动的状态转换函数j的定义是相对于“AiG函数”[11]119的所有模型,那么Kiφ∧Biφ→([doi(revise φ)]Biψ↔Ki(φ→ψ))。 其证明请参见Linder等[11]138。式(1)表明如果主体知道某一公式的否定是正确的,则对该公式的修正将导致荒谬的信念。式(2)表明在某个公式的否定不被相信的情况下,用该公式进行信念修正就等于用该公式进行信念扩展。式(3)表明如果主体事先知道φ蕴涵ψ,那么用φ进行信念修正之后,ψ就被相信。即用φ修正后的主体信念集,包含由φ所蕴涵的所有公式。 对于诸如测试、观察、交流等心智行动,虽然主体的能力与其拥有或缺乏的知识和(或)信念密切相关,但是信念的改变是一种严格意义上的主体内部的心智活动。因此,主体改变信念的能力仅由其心智状态决定,而且该能力可以用来说明主体信念所经历的变化。如果一个主体能够以某种方式改变自己的信念,那么这种信念的改变既不应该得到荒谬的信念集,也不能什么都没有改变。一个主体能够用公式φ修正其信念,当且仅当,它能用φ收缩其信念,然后用φ扩展其信念[11]124-125。 定义9:令M是某个带有状态s的克里普克模型,i是某个主体,φ是某个命题公式。信念扩展、信念收缩和信念修正行动的能力函数c可以分别定义如下: (1) c(i, expand φ)(M, w)=1 ⟺ M, wBiφ; (2) c(i, contract φ)(M, w)=1 ⟺ M, wKiφ; (3) c(i, revise φ)(M, w) = c(i, contractφ; expand φ)(M, w)。 定义(1)表明主体能够用一个公式扩展其信念集,当且仅当,该主体不相信该公式的否定。定义(2)表明主体能够从其信念集中移除某个公式,当且仅当,该主体不再认可该公式。定义(3)中的信念修正行动的能力是根据Levi等式[15]加以定义的。 命题9:对于所有主体 i和所有命题公式φ,有: 其证明请参见Linder等[11]141-142。式(1)和式(3)表明主体知道自己具有扩展和收缩其信念的能力。式(5)表明主体知道自己具有修正其信念的能力。式(2)、式(4)和式(6)分别表明主体有能力以其应有的方式改变其信念:扩展不会得到荒谬的信念集;信念收缩会导致不相信被收缩的公式;信念修正则需要先进行信念收缩,然后进行信念扩展[11]125。 Can谓词和Cannot谓词[16]可以对主体为了实现特定目标,所采取的规划的(不)正确性和(不)可行性的知识和推理进行形式化描述。Can谓词表示:主体知道执行行动α是达成φ的正确规划,当且仅当,该主体知道〈doi(α)〉φ成立;主体i知道执行α是达成φ的一个可行规划,当且仅当,该主体知道它能够执行α,即,KiAiα成立。Cannot谓词表示:主体知道它不能通过执行某个行动α来达到某个目标φ,因为它知道执行该行动不会达到所意图的目标,或者它不能执行该行动,即,主体知道执行该行动是错误的规划或是不可行的规划。 定义10:对于所有主体i,行动α和公式φ,Can谓词和Cannot谓词定义如下: (1) Cani(α,φ)≡Ki(〈doi(α)〉φ∧Aiα); (2) Cannoti(α, φ)≡ Ki(〈doi(α)〉φ∨Aiα)。 下面的命题表征了信念更新行动在其结果、执行机会和能力方面的性质[11]126。 命题10:对于所有主体i,且对于所有命题公式φ,有: 证明请参见Linder等[11]142-143。命题10表明:“任何有能力执行某个改变其信念的行动的”主体都知道该行动是可行的,并且知道该以怎样的方式执行行动,即,主体知道该行动是“以所意图的方式改变其信念的”一个正确且可行的规划。 本文定义了三种常见的信念更新模型:信念扩展、信念收缩和信念修正,并形式化地表征了:(1)执行这些行动所导致的事件状态;(2)决定主体“是否有机会执行这些行动的”条件;(3)主体为了完成这些行动所应具备的能力。同时,使用选择函数定义了信念收缩行动模型,这些函数选择主体认知选项集的一个子集,并将该子集添加到其信念选项集,从而达到收缩其信念集的目的。 未来研究可以考虑:(1)从多个来源获取信息的主体,如何对改变其心智的行动进行形式化?这时信息和来源的可靠性决定了主体是否改变其信念以及如何改变其信念。(2)如何对主体的行为动机进行形式化处理?
三、行动改变心智
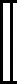
(一)信念扩展行动
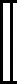
(二)信念收缩行动
(三)信念修正行动
(四)改变心智的能力
四、结论与未来的工作

