基于ACC车辆的主动换道控制
武余利, 钱志高, 张心奕, 俞宴明, 尹中亚, 冉海风
(1. 安徽工程大学 机械工程学院,安徽 芜湖 241000;2. 中国北方发动机研究所,天津 300400)
随着智能驾驶技术的快速发展,逐渐开发了自适应巡航、车道保持、换道等辅助驾驶系统。其中ACC系统的控制策略主要有模糊控制[1]、模型预测控制[2]等比较成熟的技术。对于部分自适应巡航系统只研究车辆的纵向速度控制,未考虑前车速度过低影响自车行驶情况,因此,当遇到自车长时间跟随低速行驶的前车的情况时,不能满足驾驶员的主观需求。实际换道情况[3]包括选择性和强制性换道,而选择性换道情况通常高于避障和道路合流(强制性换道),随着道路数量的增加选择性换道情况会更加频繁。驾驶员换道的主要原因是选择性换道中前车速度过低,不能满足驾驶员的主观要求。由此,本文在建立ACC系统模型基础上,还考虑了驾驶员对速度期望的要求。
车辆进行主动换道时,合适的换道轨迹至关重要,通常选择几何法,其中有正弦函数换道轨迹[4]、圆弧换道轨迹[5]、五次多项式换道曲线[6]。几何法轨迹曲线原理简单、易实现,能够满足驾驶换道要求。规划出换道期望轨迹后,选择轨迹跟踪控制算法是车辆换道的关键,以确保车辆安全、平稳、低误差的跟踪规划轨迹,常用的有滑模控制[7]、自适应控制[8]等算法。部分控制算法中参数的选择对周围环境的要求较高,且不易处理车辆的动力学约束。而模型预测控制[9]能够在车辆行驶过程中增加多种约束,提高轨迹控制跟踪效果,尤其在车辆行驶速度较大情况下,车辆的动力学特性对轨迹跟踪控制效果越明显。
本研究将驾驶员速度不满累积度[10]作为车辆是否换道的依据,根据主车与目标车道车辆的距离是否大于最小临界碰撞距离作为车辆的换道决策,如果主车不满足换道条件,则取消换道,主车将继续跟车巡航。基于三自由度车辆动力学模型,使用模型预测控制算法对规划轨迹进行跟踪,建立具有ACC功能和主动换道功能的控制系统,既能实现传统意义上的跟车与巡航,也能实现主动换道,进一步提高了驾驶员的驾驶舒适度和安全性。
1 自适应巡航控制系统
本研究建立的车辆ACC控制系统由上、下两层控制器组成。上层控制器为决策层,使用PID[11]定速巡航控制和LQR的距离跟踪控制模型,计算车辆的期望加速度。根据车载毫米波雷达探测行驶车道是否有车,选择不同的跟车巡航模式。下层控制器根据上层控制器计算的期望加速度,对车辆进行加、减速控制,车辆纵向行驶的加、减速由油门和刹车决定,最终实现车辆的定速巡航和车距保持。
1.1 逆纵向动力学模型
1.1.1 节气门 当车辆行驶需要减速时,期望加速度减小,车辆将切换为节气门控制,通过减小节气门开度,使行驶速度降低。由期望加速度可求得期望发动机扭矩
(1)
式中,Tdes为发动机扭矩;ades为期望加速度;f为滚动阻力系数;CD为空气阻力系数;A为迎风面积;g为重力加速度;v为本车车速;r为车轮半径;τ为扭矩函数;ωe为发动机转速;η为传动效率;Rg和Rm为变速器和主减速器传动比。
1.1.2 制动压力 根据车辆行驶的周围环境,需要减速制动时,车辆将切换成制动压力控制模型,期望的减速度转换成制动压力,以保证车辆减速,避免车辆间的碰撞。制动压力公式为:
(2)
式中,Pb为制动压力;Kb为增益系数;在Simulink中建立的制动压力控制模型如图1所示。
1.2 基于LQR控制的ACC系统控制策略
在软件Carsim中设置自车、前车速度与初始相对距离。根据车载传感器探测当前车道是否有车,以此确定本车行驶模式。跟车模式以两车相对距离与期望安全距离之差、期望速度与实际速度的差值及自车的加速度为LQR控制器的输入,定速巡航以期望速度与实际速度之差作为PID控制器的输入,输出为期望加速度。在Simulink中搭建了自适应巡航系统模型[12],如图2所示。
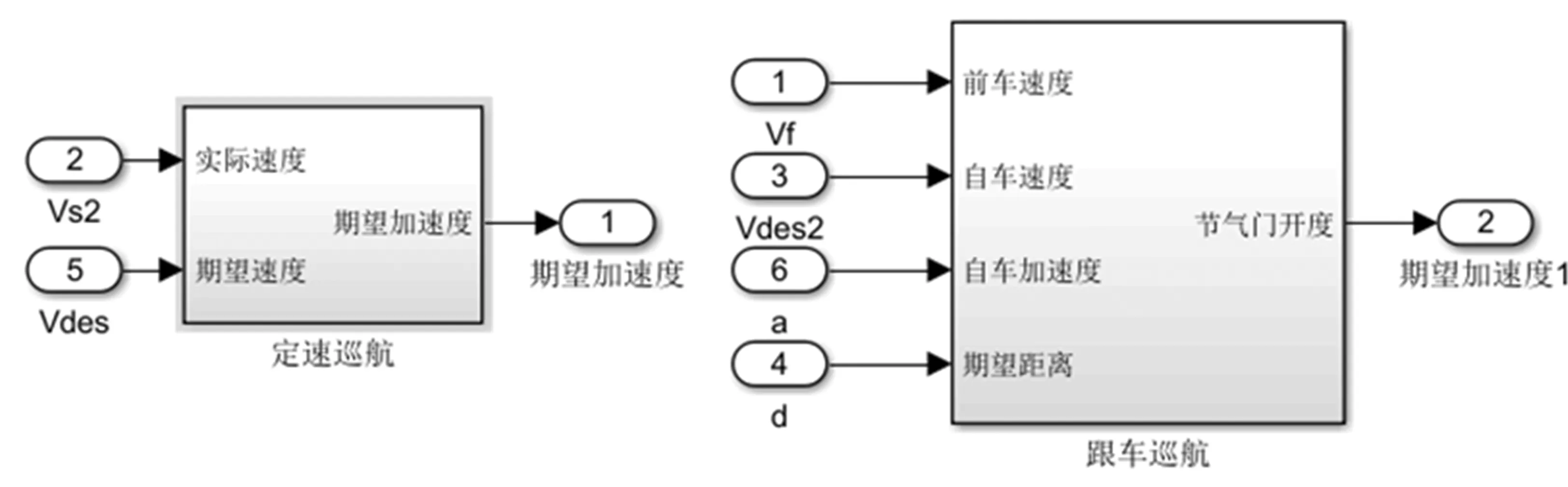
图1 制动压力与节气门模型

图2 车辆的定速和跟车巡航模型
2 主动换道分析
根据自车行驶速度未达到期望速度作为车辆换道意图的产生依据[13]。如图3所示,当自车未检测到当前车道前车时,自车进行定速巡航,检测到前车时车辆将进行自动跟车模式。当自车速度小于期望速度,并持续一段时间,且目标车道前车高于当前车道前车速度,驾驶员产生换道意图。随着时间推移,速度不满意度增加到一定值,车辆将开始准备换道。由于换道过程需要考虑周围车辆的最小临界换道安全距离,在满足安全距离条件下,车辆开始主动换道。换道完成后根据目标车道前方是否有车,来决定车辆执行定速巡航或自动跟车巡航。

图3 主动换道流程
2.1 换道意图的产生
当车辆正常行驶时,在跟车过程中发现当前车道前车速度一直处于低速状态,使得自车实际速度无法达到理想的期望速度。通过设置一个定量数值作为主车是否换道的条件,当主车在跟随当前车道前车时,速度始终没有达到设定的期望速度,随着时间的推移期望速度与实际速度的差值将不断累积,便有了车辆行驶时的速度期望不满累积度公式:
(3)
式中,C为速度不满累积度,Vdes为自车期望车速,V为自车实际车速,T为采样时间,k为当前时刻。
2.2 换道过程的可行性分析
当前车速度处于持续过低状态,速度不满累积度超过一定的值后,智能车辆便开始准备换道,然而还需要根据自车周围车辆信息是否存在安全距离来确定能否换道,如下图4所示车辆所处的情况。将最小临界碰撞距离作为换道时与目标车道前后车辆所保持的最小安全距离,即最小安全距离(MSS)[14]。本车与前车总是保持一定的安全距离,速度接近甚至略小于前车车速,故只需要考虑旁边车道前、后车的最小安全距离。
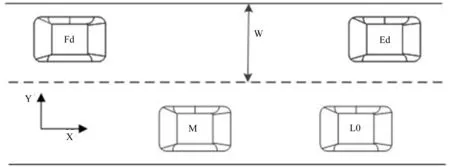
图4 车辆所处示意图
2.2.1 M车与Ld车的最小安全距离 主车为M车,换道期间目标车道前车(Ld)车处于车道保持的行驶状态,在换道期间两车匀速行驶,加速度均为零。主车在直线换道期间不发生碰撞的最小安全距离公式为:
(4)
其中,LM为自车车身长度;tθ为自车车速方向与车道线的夹角;tp1为两车临界碰撞时刻。
2.2.2 M车与Fd车的最小安全距离 目标车道后车(Fd)也处于车道保持的行驶状态,在换道期间两车匀速行驶,加速度均为零。M车最小安全距离公式为:
(5)
式中,t∈[tp2,tc],tp2为换道临界碰撞时刻;VM、VLd为分别为M车与Fd车的纵向速度;LM、wm为自车长度和宽度。
3 换道轨迹规划与控制
3.1 轨迹规划
在多项式曲线中,五次多项式换道曲线计算简单,由于换道过程速度不变加速度为零等因素,根据车辆换道初始、完成时的位置、速度,加速度等实时状态,可以得到如下公式6的车辆换道轨迹。如下图5所示,相比较于三次和七次曲线它的曲率连续且光滑,换道过程的舒适性、安全性更优,满足换道轨迹的要求。X轴为车辆纵向行驶速度方向,Y轴为车辆换道的横向位移方向。本研究建立的ACC系统规划轨迹满足下列约束。
(1)换道初始位置坐标为(0,0);
(2)换道终点位置的坐标为Y(tc)=3.75 m,换道总时长tc为4 s;
(3)换道初始横向位移、横向速度为零,纵向速度为跟车模式下的 v0换道过程速度不变;
(4)换道完成时车辆的横向速度和加速度均为零;
由此可得五次多项式换道规划轨迹为:
(6)
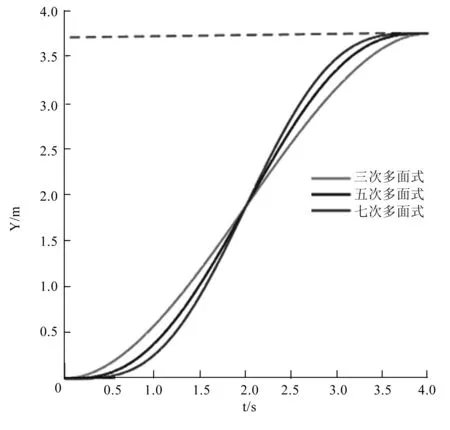
图5 多项式换道曲线
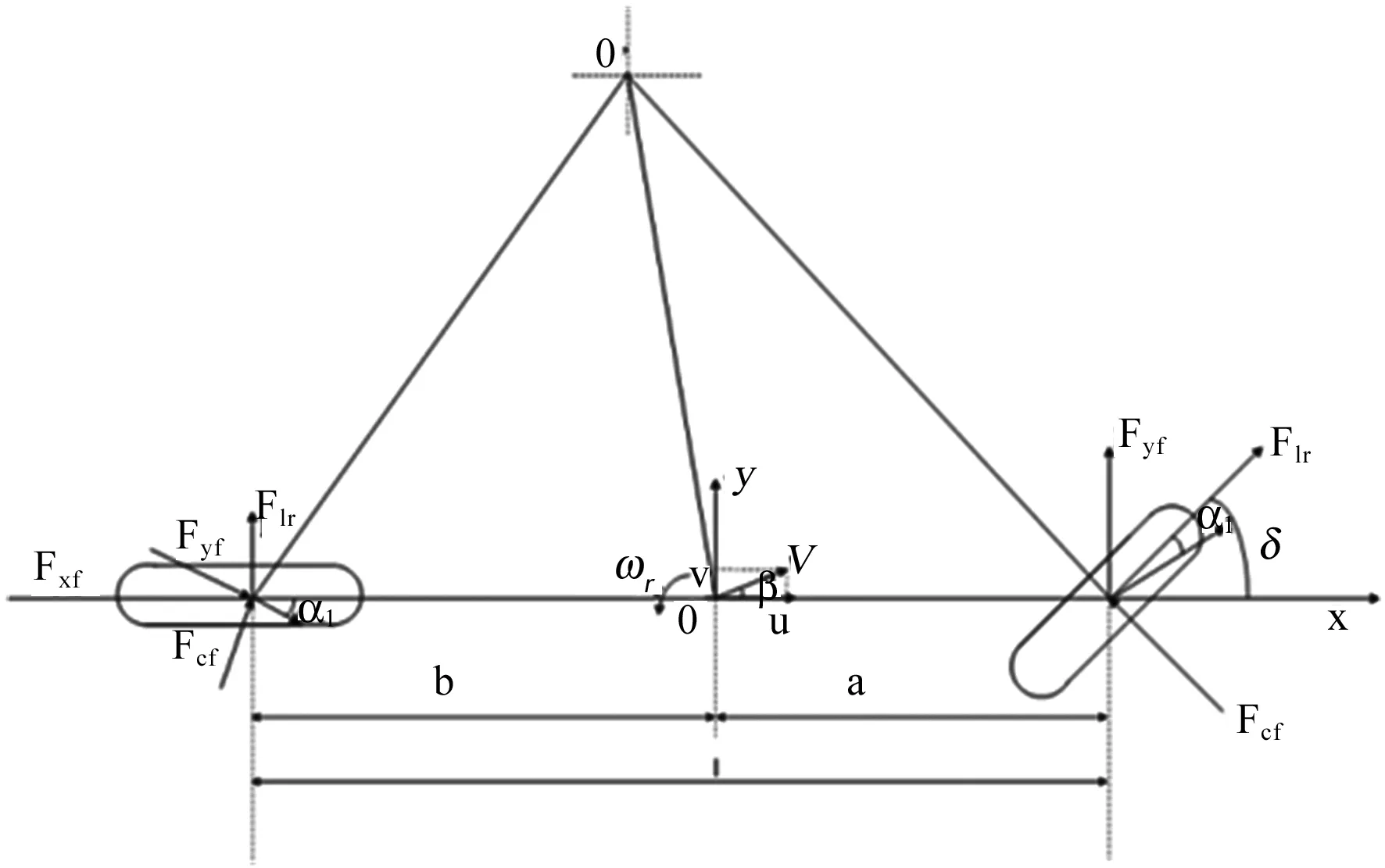
图6 车辆三自由度模型
3.2 模型预测控制
本研究采用三自由度车辆动力学模型,基于模型预测控制算法对规划的五次多项式换道轨迹进行跟踪。车辆的行驶状态信息一直在不断变化,它能够根据输出结果进行反馈校正,以期车辆的行驶轨迹能够接近规划轨迹,完成车辆的跟踪控制。
本研究通过建立车辆动力学模型[15]预测下一时刻车辆的行驶位置,仅分析车辆横向、纵向以及绕Z轴横摆三个自由度方向的运动,而不考虑与车辆平顺性相关的悬架.根据牛顿力学第二定律,分别列出沿x,y和z轴的受力平衡方程。
(7)
汽车轮胎在x、y行驶方向上纵向力、侧向力为:
(8)
式中,δr、δf为分别后、前轮转角,当车辆开始换道时,δr=0。
汽车行驶时车辆轮胎受力主要受滑移率S、轮胎侧偏角α、路面附着系数μ、垂向载荷Fz的影响,关系如下:
(9)
其中,μ为路面摩擦因数,FZ为轮胎的垂向载荷,α为轮胎侧偏角,s为滑移率。
前、后轮胎侧偏角α为如下:
(10)
车辆行驶的轮胎纵向滑移率S为:
(11)
式中,vl表示轮胎旋转角速度,rw表示轮胎半径。
假设车辆行驶过程中没有急剧加速和制动,前后车轮垂直受力为:
(12)
在侧向加速度小于0.4的情况下,由式12可得,根据小角度假设可以建立车辆动力学模型:
(13)
式中,a、b为车辆质心到前、后轴的距离;m为整车质量;IZ为车辆绕z轴的转动惯量。控制量是前轮转角δf,状态量是[y,x,Φ,Φ,Y,X]。输出量是η(t)=[Φ,Y]T。其主动换道控制系统如图7。

图7 换道控制流程
4 仿真结果分析
本研究采用仿真软件CarSim中C级车自带的动力学模型,根据仿真需求设置仿真工况中周围车辆状态和车身参数。选用125 kW的发动机,其他车辆参数设置均保持默认。对目标车道前方是否有车,进行仿真验证,换道过程中的质心侧偏角、横摆角、横摆角速度的变化相同。仿真车辆参数见表1。

表1 车辆部分参数
4.1 目标车道前方无车
为实现自适应巡航车辆能够主动换道和换道后车辆的行驶状态与期望的一致,将通过仿真实验进行验证。在CarSim中设置当前车道的前车以50 km/h的速度匀速行驶,本车与前车的初始位置距离为80 m,本车的定速巡航速度为72 km/h,周围环境没有干扰车辆。
从图9可以看出,本车以60 km/h的初速度逐步加速至设定的巡航车速72 km/h,行驶一段距离后,雷达传感器检测到前方有正常行驶的车辆,这时本车将进行速度模式切换,对前车进行跟驰,本车车速先上升、快速接近前车然后逐渐下降,逐渐达到期望的安全跟车距离。在一段时间内本车车速持续小于期望车速,驾驶员便产生了换道意图,速度不满意度逐渐积累,当达到阈值6时,本车执行换道,换道完成后继续以设定巡航车速匀速行驶。图8所示车辆完成换道,从当前车道按照规划的五次多项式换道轨迹行驶至目标车道,换道的横向距离为3.75 m。图9所示车辆先后经历定速巡航,跟车巡航,匀速换道,定速巡航4个主要车速变化。
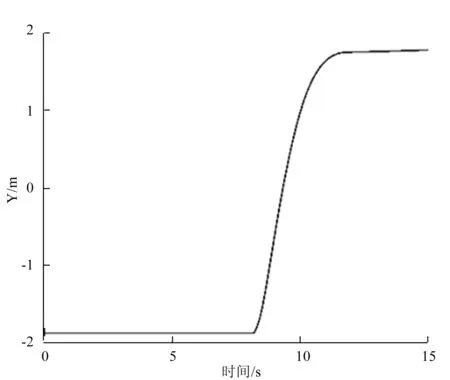
图8 车辆行驶轨迹

图9 车辆纵向速度
如图10~12所示,在换道过程车辆能够保持平稳,安全。横摆角速度,质心侧偏角,横摆角波动值均在合理范围内,由此得出基于模型预测控制的轨迹跟踪效果良好,满足驾驶换道要求。

图10 横摆角速度Fig.10 Yaw rate图11 横摆角Fig.11 Yaw angle 图12 车辆质心侧偏角Fig.12 Side deflection angle of vehicle centroid
4.2 目标车道前方有车
本车与前车的车速、初始距离与上一工况中数据一样,但是本工况考虑了相邻车道存在行驶车辆,设置相邻车道的前、后车匀速行驶,速度为60 km/h,两车相对距离为155 m。本车与相邻车道前、后车纵向距离分别为70、85 m。
从图13可以看到,本车从初速度60 km/h逐步提速至巡航车速,当发现当前车道有车时,本车将行驶模式切换为自动跟车模式,速度逐渐上升以接近前车,充分利用道路使用率,当达到期望的安全距离时车辆将会进行减速跟随前车,避免发生碰撞。当本车实际行驶速度逐渐下降并低于本车设置的巡航速度72 km/h时,随着时间增加,驾驶员将会产生换道意图,速度不满意度也在一直累积,当速度不满意累积度达到阈值6时,主车发现目标车道前车速度高于当前车道前车车速,满足换道安全条件,换道完成后,本车跟随当前车道前车以60 km/h的速度匀速行驶。
如图15~17所示横摆角速度,质心侧偏角,横摆角波动值均在合理范围内,满足驾驶换道要求。

图13 车辆行驶轨迹
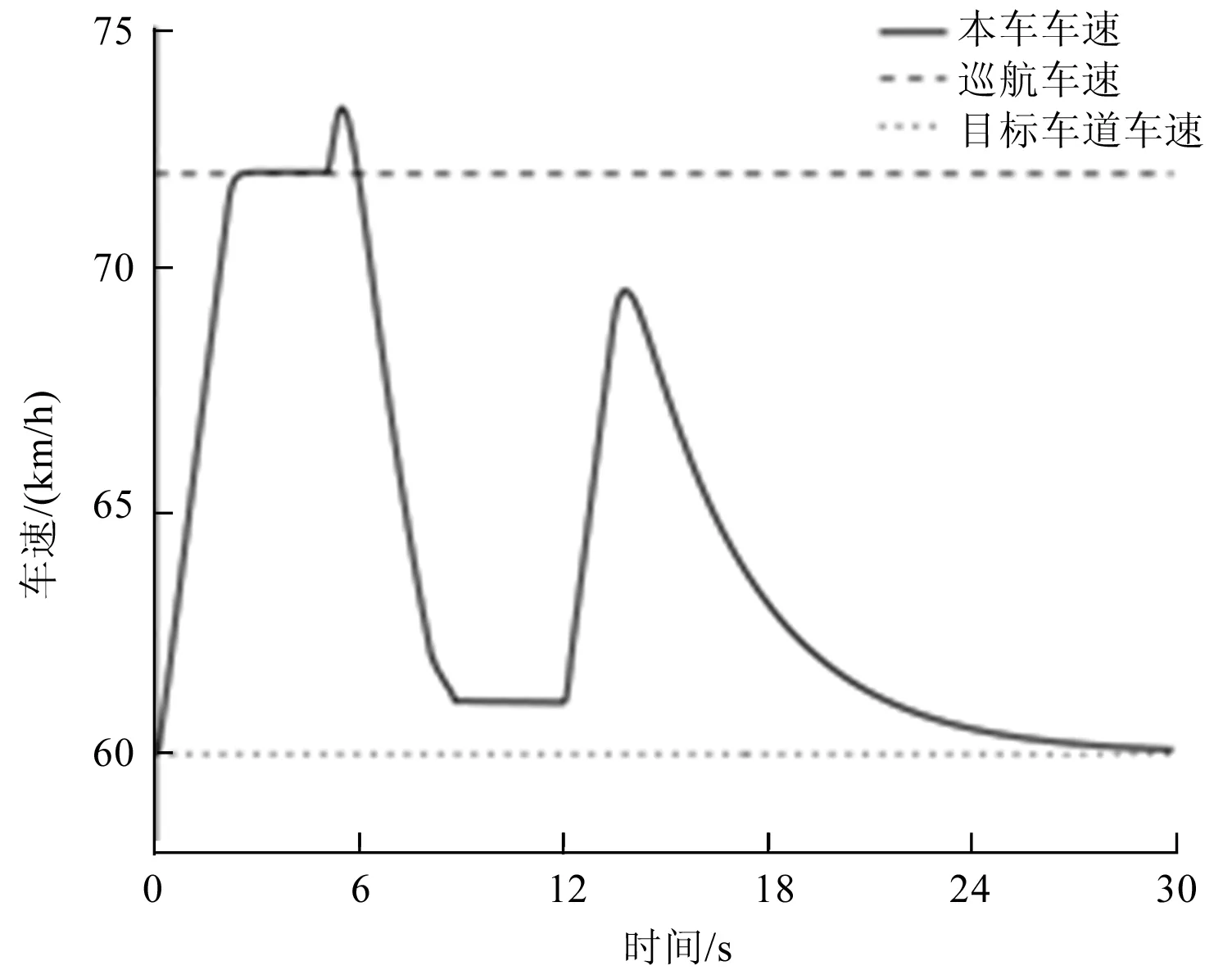
图14 车辆纵向速度
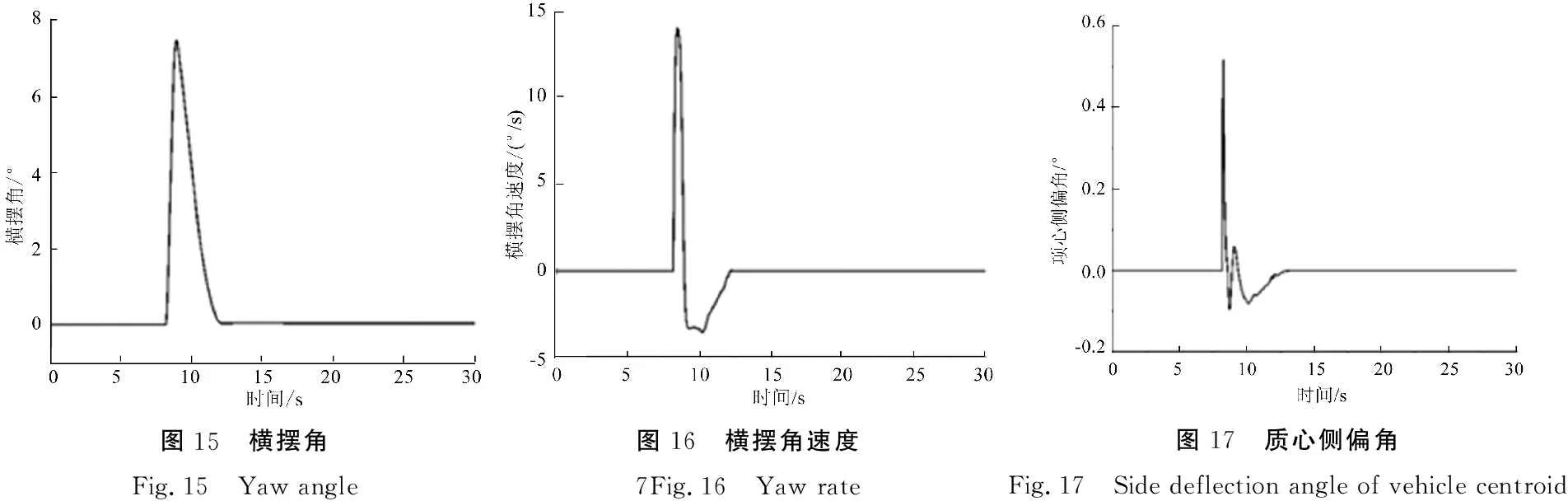
图15 横摆角Fig.15 Yaw angle图16 横摆角速度7Fig.16 Yaw rate图17 质心侧偏角Fig.17 Side deflection angle of vehicle centroid
5 结论
在传统ACC系统模型基础上,考虑到驾驶员的换道意图,建立车辆逆纵向动力学模型,基于LQR控制的ACC系统自动跟车控制策略,实现了自适应巡航系统的定速巡航和自动跟车的功能。提出一段时间内车辆行驶速度持续低于期望速度作为自适应巡航车辆的换道意图,使用最小临界碰撞距离作为换道决策,采用模型预测控制算法对规划的多项式曲线进行跟踪控制。设置目标车道前方是否有车的两种工况,使用Simulink/CarSim软件对建立的模型进行联合仿真,结果表明,采用本研究的主动换道控制策略,能够实现传统意义上的定速巡航与自动跟车,也可满足驾驶员换道意图的主动换道,从而提高了驾驶员驾驶舒适度和安全性。

