双足压电直线电机定子系统建模与实验

邸志民， 钟相强， 方华杰， 冯赛龙， 范敬松

(安徽工程大学 机械工程学院，安徽 芜湖 241000)

压电直线电机具有运动轻巧、结构简单、工作运行稳定和精度高等优点,该类型电机能够在低温、高温、电磁干扰、真空等环境下安全有效工作[1-2],而传统电机采用电热、电磁或机械式驱动,由于工作原理等原因不能满足现有的工作要求[3-5]。双足压电直线电机利用了杠杆放大式双足定子为驱动元件,可以驱动工作台工作,并能精确定位。

20世纪40年代,BaTiO3的发现,使压电作动技术迅速发展。徐晶晶等[6]设计了一种单足驱动型压电直线电机,对电机运动轨迹通过实验进行验证,但对机构复合放大率并未探究,也未进行动力学建模分析。对一种动摩擦型压电叠堆单足直线电机定子进行了实验研究,推导了其驱动端的微分方程,实验验证了此类电机的谐振特性,但对其速度未进行分析[7-9]。本研究针对双足压电直线电机定子系统建模,并通过实验研究驱动足的振幅、速度等来验证电机的工作性能。首先,建立双足压电直线电机定子结构、定子系统二自由度横向振动系统和电机速度测试实验装置;其次,基于正交实验对双足压电直线电机速度性能进行极差和方差分析。从而验证该压电电机具有驱动位移大、速度反应快和工作稳定等特性。

1 双足压电直线电机定子系统动力学建模

1.1 双足压电直线电机定子结构模型和原理

双足压电直线电机定子由压电叠堆、预紧机构、预紧力调整机构、柔性铰链、驱动足(二级杠杆)等组成[10-12]具体结构如图1所示。

利用相位差为π/4的两正弦电压对4个压电叠堆分别进行激励,同时电机定子系统产生振动,并在驱动端处形成运动轨迹。预紧力调整机构使驱动足与动子接触,使电机定子和动子之间产生摩擦所需要的正压力,以便能驱动动子运动。

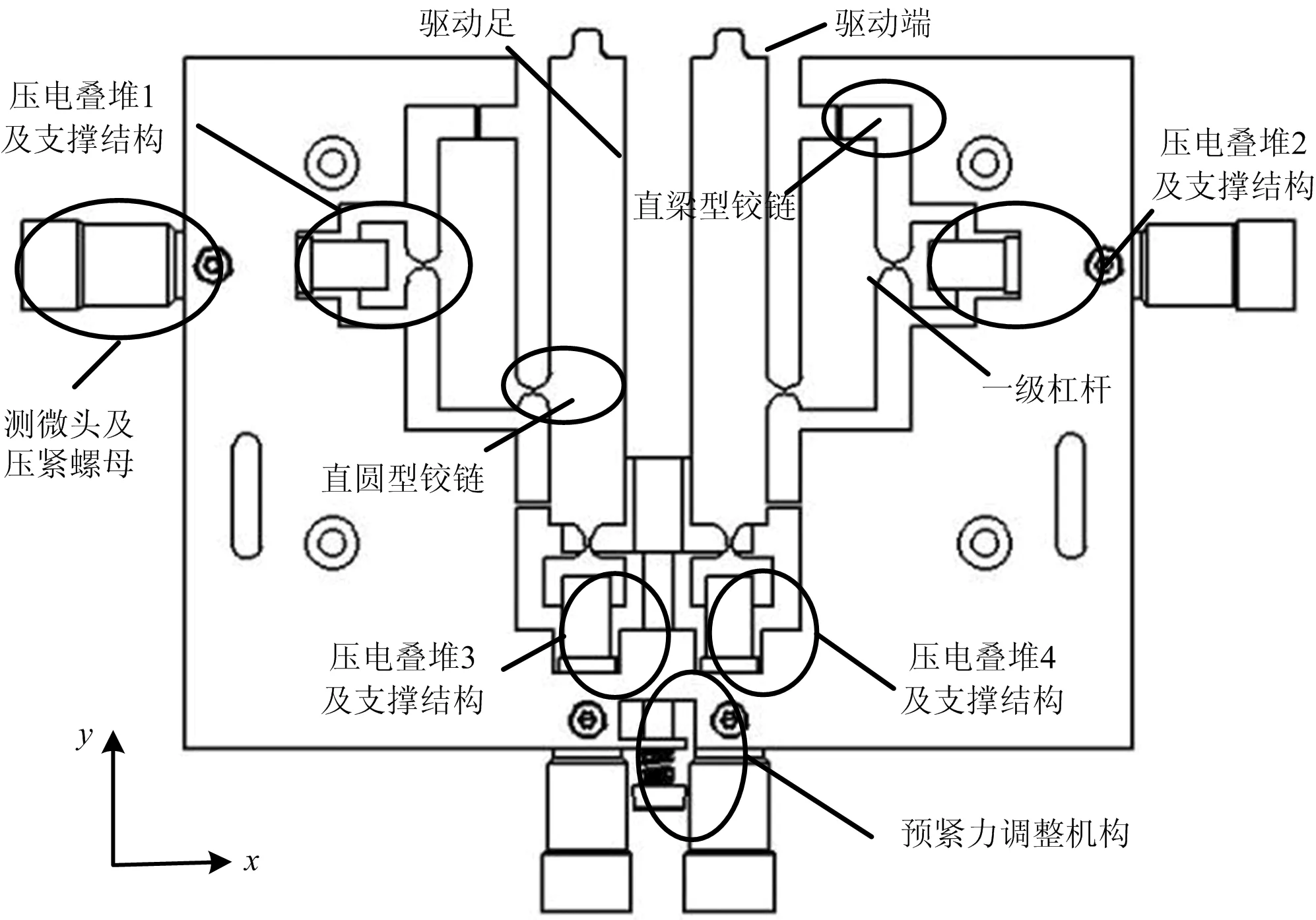
图1 双足压电直线电机定子结构

1.2 双足压电直线电机定子系统振动特性

由于压电叠堆的输出位移比较小,因此系统阻尼会非常小,对纵向(图1中y方向)振幅几乎不产生影响,则系统阻尼可以忽略,本研究主要考虑电机驱动足的横向振动(图1中x方向)[6]。直圆型柔性铰链和直梁型柔性铰链可看作纯弹性元件,因为它们符合小变形理论的基本假设。根据电机的结构和工作原理,由于对称性,可以取图1左侧为分析对象,将其简化为二自由度横向振动系统,如图2所示,由电机定子、柔性铰链、一级杠杆和驱动足(二级杠杆)组成[13]。其中:m1为定子驱动足的质量;m2为定子一级杠杆的质量;k1为一级杠杆与驱动足之间的直圆型柔性铰链的刚度;k2为压电叠堆和一级杠杆之间直圆型柔性铰链的刚度之和;k3为定子与驱动足之间直梁型柔性铰链的刚度;y1(t)为驱动足的横向位移,y2(t)为定子一级杠杆的横向位移;F1(t)和F2(t)为压电叠堆输出力在横向的合力,F3(t)为直梁型柔性铰链所施加的力。

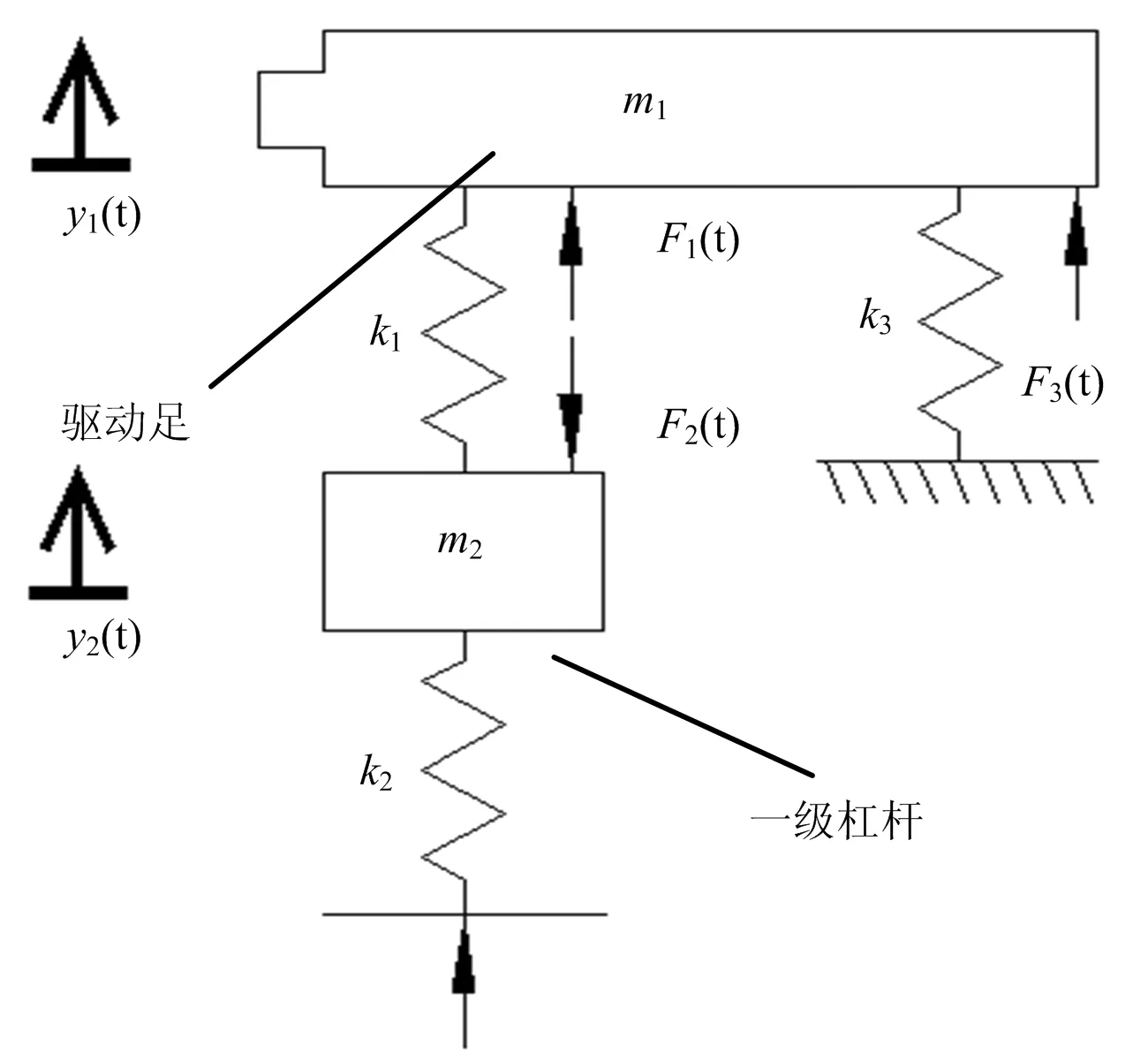
图2 定子的横向振动系统

由图2可得定子横向振动系统的微分方程:

(1)

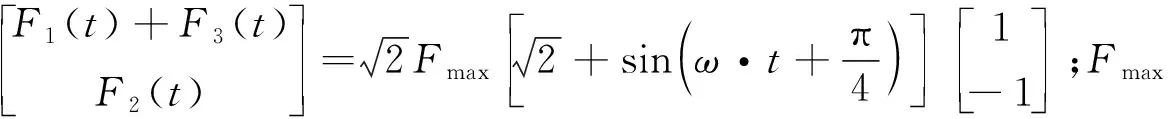
代入,求解得:

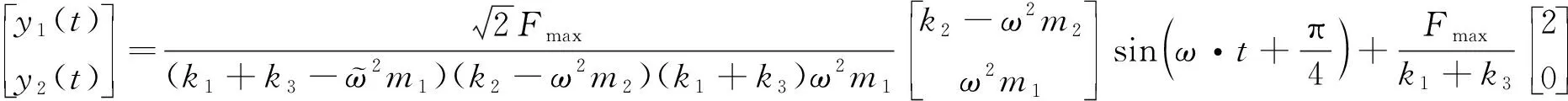
(2)

由式(2)可得:

(3)

因此,可得振幅A的表达式为:

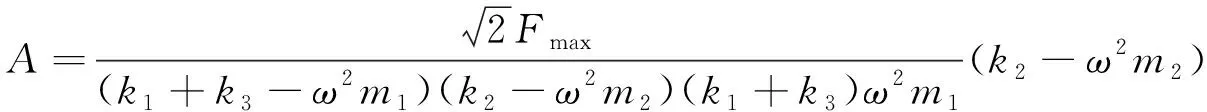
(4)

根据压电直线电机中定子系统的二级杠杆模型,测量并计算它们的体积,得到第一级杠杆体的体积为2 280 mm3,第二级杠杆的体积为4 018.1 mm3,由m=ρv,可得到第一级杠杆质量为0.017 9 kg,第二级杠杆的质量为0.031 5 kg。由压电直线电机模型的主要结构参数决定了定子横向振动位移模型的等效结构参数,如表1所示。

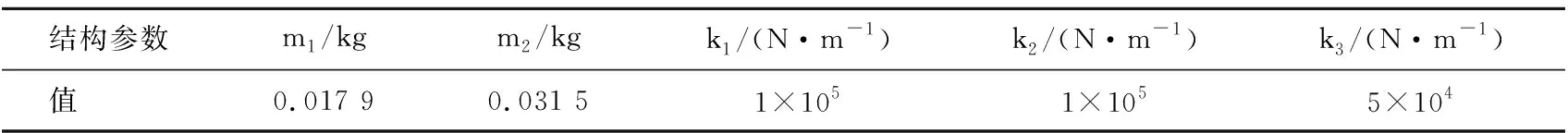
表1 压电直线电机定子系统等效结构参数

将表1中的数值代入式(4)中,便可得到驱动足的振幅数值为61 μm。如图3为电机定子驱动足振幅实验系统,其中1定子,2为固定定子1的夹具,3为定子驱动足,4为Laser XL-80激光位移传感器。首先产生一路100 Hz的三角波信号,并将电压放大到120 V,使驱动足运动。通过激光位移传感器对驱动足位移进行测量,并将测得数据上传到计算机中。实验测试结果如图4所示,驱动足的振幅在61 μm左右,与理论计算结果相符。

图3 定子驱动足振幅测试装置

图4 驱动足I的振幅

2 基于正交试验的双足压电直线电机速度性能分析

2.1 实验分析

上述理论模型和振幅测试能够证实该双足压电直线电机设计的正确性,但无法进一步得出电压和频率对电机速度的影响大小,因此,对速度实验数据进行整理,用正交实验设计的方法进行分析处理,找出影响压电直线电机速度的因素,并且得出相应的关系,图5为测试压电电机速度的实验装置,其中1为压电电机定子,2为4路信号发生器,3为示波器,4为功率放大器。

图5 压电电机速度实验装置

2.2 确定试验因素、水平和指标

本实验分析了电压、电压频率对速度的影响,分别用X1和X2进行表示。选取最初的数据为实验的基本参考数据(表2),其它数据值则以此作为标准上下浮动,变动的幅度值为10 V和10 Hz。确定各个因素的水平数为6,即对应电压X1的值(分别为70、80、90、100、110、120 V),对应电压频率X2的值(50、60、70、80、90、100 Hz)。

表2 试验因素及水平

2.3 试验结果

通过实验、数据分析,将电压、电压频率对速度的影响用折线图表示(图6～7)所示。可以看出,随着电压和频率的增加,电机的速度都在增大;但无法得出电压、电压频率对电机速度影响的精确关系,要想得到准确的关系,需要运用极差、方差分析法对实验数据进行进一步的比较与分析。

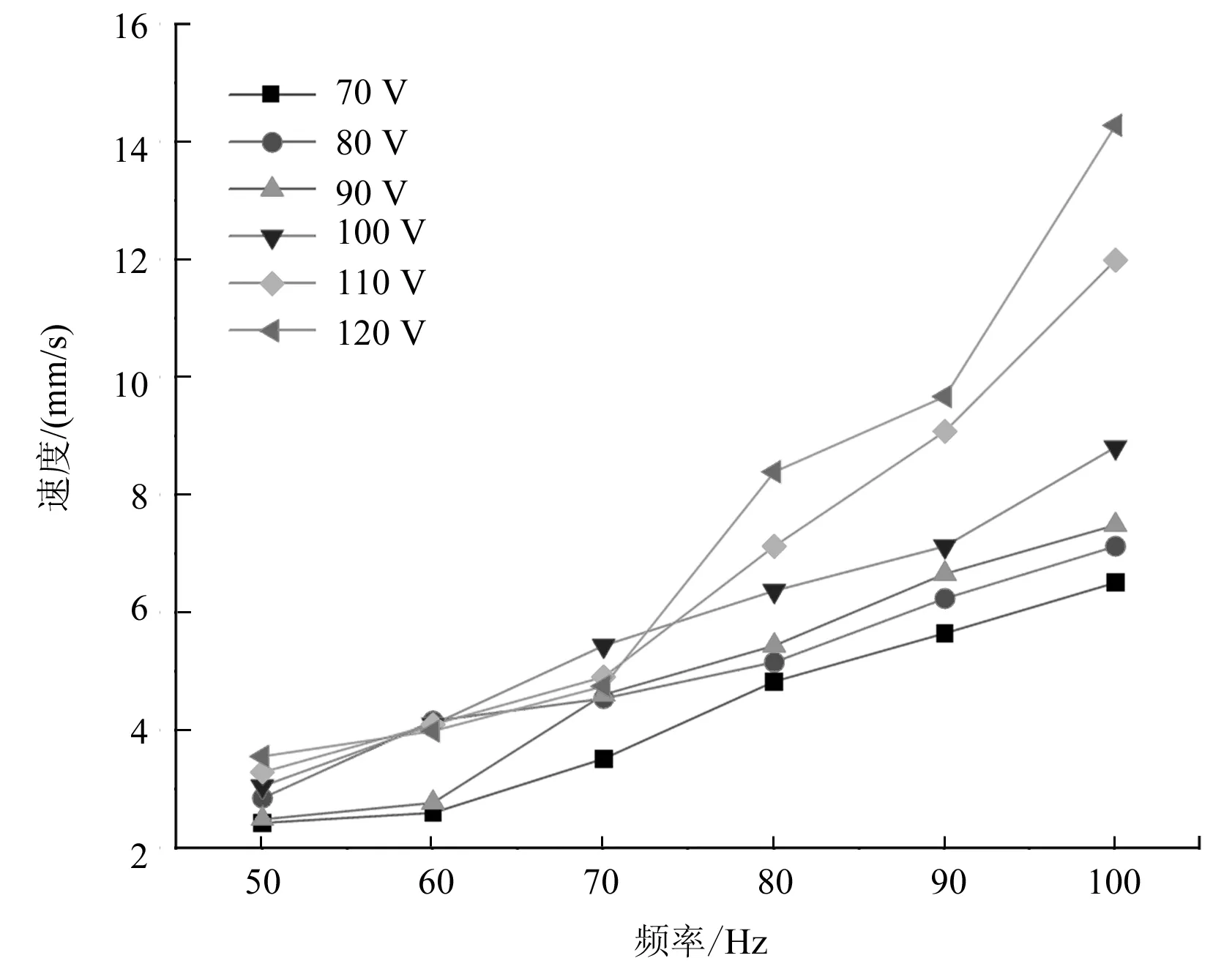
图6 不同电压频率下速度曲线

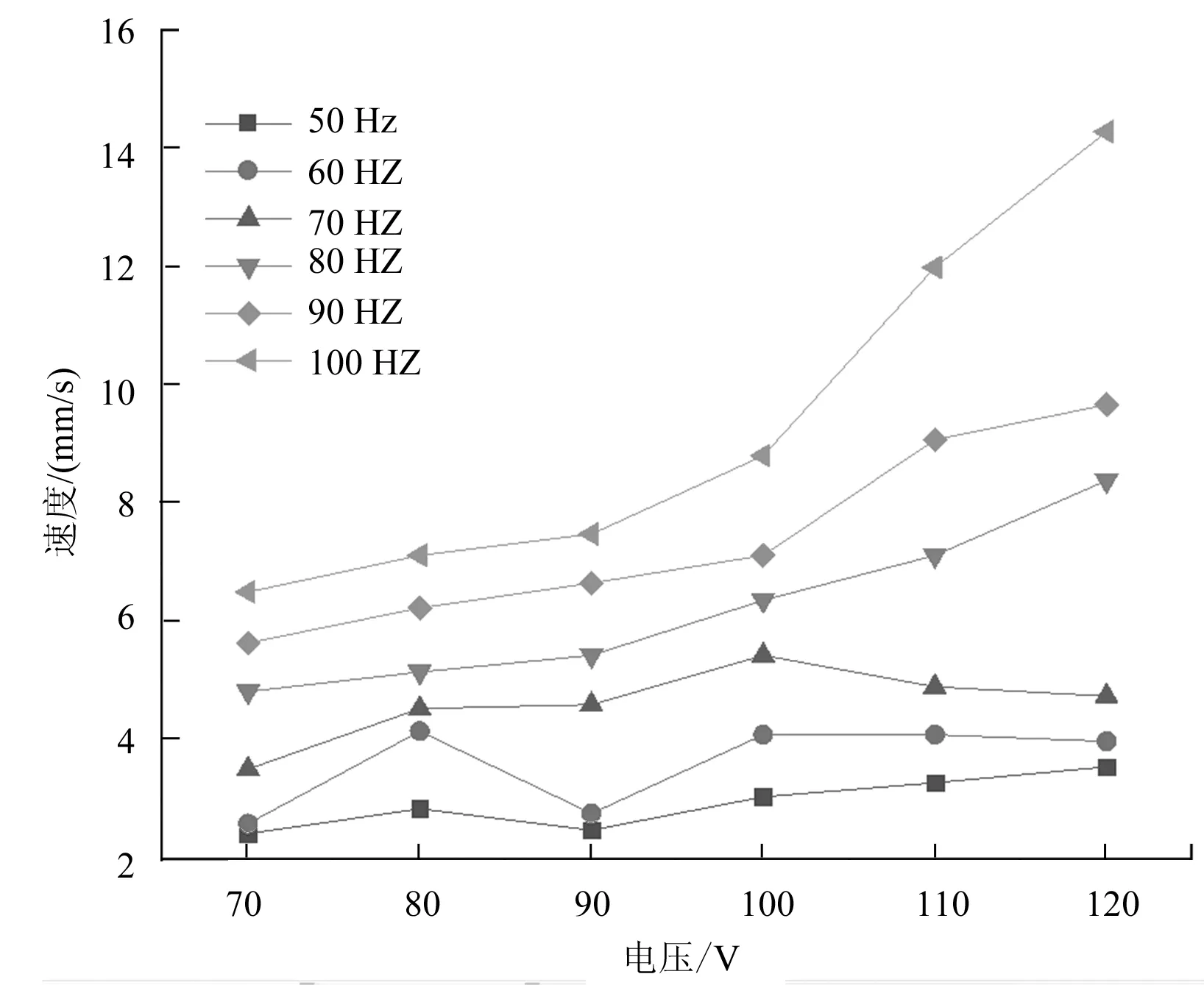
图7 不同电压下速度曲线

2.4 极差分析

对实验数据进行极差分析得到双足压电直线电机的极差分析表,K为水平因子,R为极差(表3)。

表3 极差分析表

由表3可以看出,双足压电直线电机的速度同时受到电机的电压频率和电压影响,且电压频率X2的极差大于电压X1的极差,极差:RX2>RX1。

2.5 方差分析

由求解方差的方法解得双足压电直线电机速度的方差值,其中e为误差列。由表4～表5可知,双足压电直线电机的电压和电压频率的F值都大于方差临界值F=8.47,表明电压和电压频率都对速度有影响,而且其中电压频率的F值远大于电压的F值,说明电压频率对双足压电直线电机速度的影响更为显著。

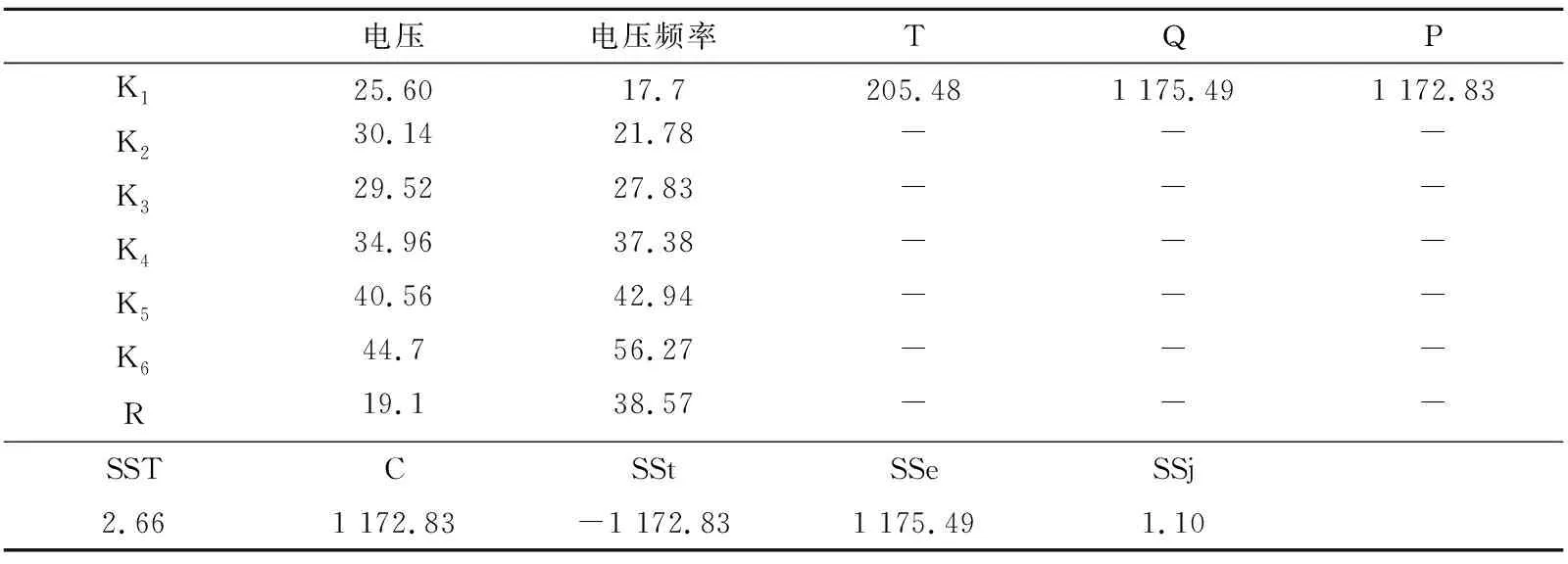
表4 速度方差计算参数

表5 速度试验结果的方差分析

3 结论

研究双足压电直线电机定子系统动力学建模方法,建立双足压电直线电机定子的动力学模型,经过理论计算得到驱动足的振幅为61 μm,与实验值相一致。基于理论计算结果对电机定子、柔性铰链、第一级杠杆和驱动足进行结构设计,并对电机模型的驱动足振幅、速度进行了实验分析。结果表明,速度受到电压频率和电压的影响,电压频率对速度的影响更加显著。分析结果验证了压电电机符合理论设计要求,且电机结构简单,工作稳定,为后续研究压电电机提供了理论依据。