空间交错隧道施工围岩应力影响范围及粘接锚杆作用机理的研究

黄春晖, 赵春晨, 王扶义

(陕西工业职业技术学院, 陕西 咸阳 712000)

随着我国交通工程的快速发展，大量的铁路、公路隧道及城市地铁、排水设施等隧道工程被修建或即将新建，由此，不可避免会产生大量的新建隧道邻近既有结构物的近接施工工程，如何保证这些近接工程的安全施工，既不造成原有隧道的破坏，也要避免既有隧道对新建隧道的施工产生不利影响就成了一个亟待解决的问题。

目前，国内外学者针对此类近接隧道施工相互影响的问题已进行了研究报道。其中，以长春地铁1号线04标段施工地表沉降监测数据，分析了后行隧道开挖对先行隧道地表沉降的变化规律和量值大小；房明等提出了交叉隧道盾构施工引起既有隧道沉降计算的随机介质理论方法，建立了交叉隧道盾构施工引起既有隧道沉降的计算模型，并探讨了计算参数的选取方法；针对铁路双线立体交叉隧道结构，通过数值模拟和回归分析等方法对不同围岩级别条件下既有隧道受新建隧道施工的影响情况进行了研究。以上现场实测、模型计算、数值模拟3种方法也是研究此类工程的有效手段，但研究内容多以变形沉降变形为主而缺乏对围岩应力的研究。因此，本文以贵州省某市机场高速公路夏家岩隧道上穿贵昆铁路塔山脚隧道为背景，利用MIDAS/GTS有限元软件建立不同近接竖距下的空间交错隧道有限元模型，对不同近接竖距下“上穿”新建隧道和下部既有隧道围岩应力的变化规律及对基于该工程地质状况的围岩应力变化影响范围进行研究。

1 拟建工程概况

夏家岩隧道位于贵州省某市机场高速公路，该高速公路等级为：双向四车道高速公路，隧道设计速度80 km/h。夏家岩隧道采用分离式设计，左洞长560 m，起止桩号ZK2+690～ZK3 +250；右洞长555 m，起止桩号YK2+705 m～YK3+250 m，隧道主洞建筑限界如表1所示。该隧道出口段150 m内正交上穿贵昆铁路塔山脚隧道，二者设计高程差为30 m，交错段公路隧道埋深31～50 m。

表1 夏家岩隧道主洞建筑限界表

2 空间交错隧道有限元模型的建立

利用有限元软件 MIDAS/GTS 模拟隧道“上穿”新建隧道和下部既有隧道在空间垂直交错时的开挖和支护施工，研究其动态施工力学变化规律。新建隧道从既有隧道上方以一定距离正交穿过，为了寻求隧道围岩应力随着两隧道近接距离的变化规律，既有隧道铁路塔山脚隧道高程固定，“上穿”高速公路夏家岩隧道高程逐渐增大，即两隧道间距逐渐增大，隧道轴线之间的交角始终为正交。立交点处上隧道仰拱底与下隧道拱顶间距分别为：1、2、3、5、7、10、15和20 m此8种近接情况分别建立三维模型，并定义为工况1、工况2、工况3、工况4、工况5、工况6、工况7、工况8。

2.1 分析断面的选取

有限元模型选取夏家岩隧道左洞和塔山脚隧洞的相交部分进行分析计算，由夏家岩隧道的地勘报告及设计图纸可知，两隧道交叉段位于夏家岩隧道出口端150 m处，隧道洞身段埋深20～35 m，地表覆盖第4系黏土2～5 m，下伏中分化灰岩。建模时模拟隧道处于中风化灰岩中，并且上部覆盖等厚的5 m人工填土。

考虑夏家岩隧道实际开挖尺寸以及数值模型的单元数量多少对计算速度的影响，计算模型选取：长80 m、宽80 m、高65 m。上层隧道最大开挖宽度为10.8 m，开挖高度8.6 m；下层隧道最大开挖宽度为7.50 m，开挖高度8.05 m。模型的边界范围：上部新建隧道左侧和右侧约为洞跨的3.5倍，下部既有隧道左侧和右侧均约为洞跨的5倍，隧道底部约取洞跨的2倍，隧道顶部埋深取顶部实际埋深均值30 m。建立的8种工况有限元模型结果如图1所示。

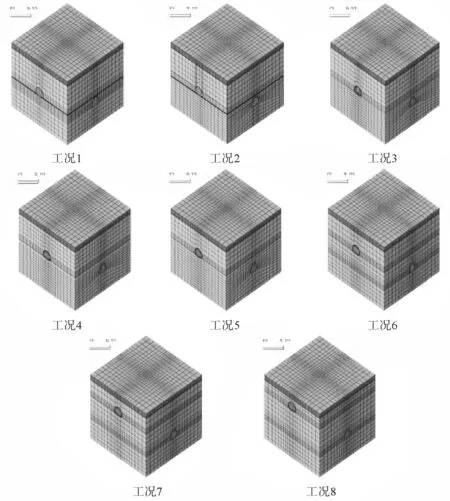
图1 8种工况有限元计算模型

2.2 边界条件及荷载的选取

模型上部边界为自由面，其余各面施加法向约束，隧道周边节点为自由界面。由于空间交错部分所处围岩较差，以Ⅳ级围岩为主，模型中应力释放系数分别取开挖隧道时0.5，初期支护时0.3，2次衬砌施作时0.2；也即围岩应力在隧道开挖时释放总应力的50%，初期支护施作时应力释放总量的30%，2次衬砌施作时应力释放总量的20%。

2.3 模型参数的选取

有限元模型中围岩和支护结构参数按照夏家岩隧道地勘报告，并结合《公路隧道设计规范》(JTG 3370.1—2018)进行选取。具体的参数取值如表2、表3所示。

表2 围岩特性值

表3 支护结构特性值

3 新建隧道“上穿”前后下部既有隧道围岩应力变化分析

3.1 “上穿”新建隧道开挖前后下部既有隧道围岩各方向应力变化

新建隧道开挖前后下部既有隧道围岩、、方向主应力等值线图，结果如图2所示。

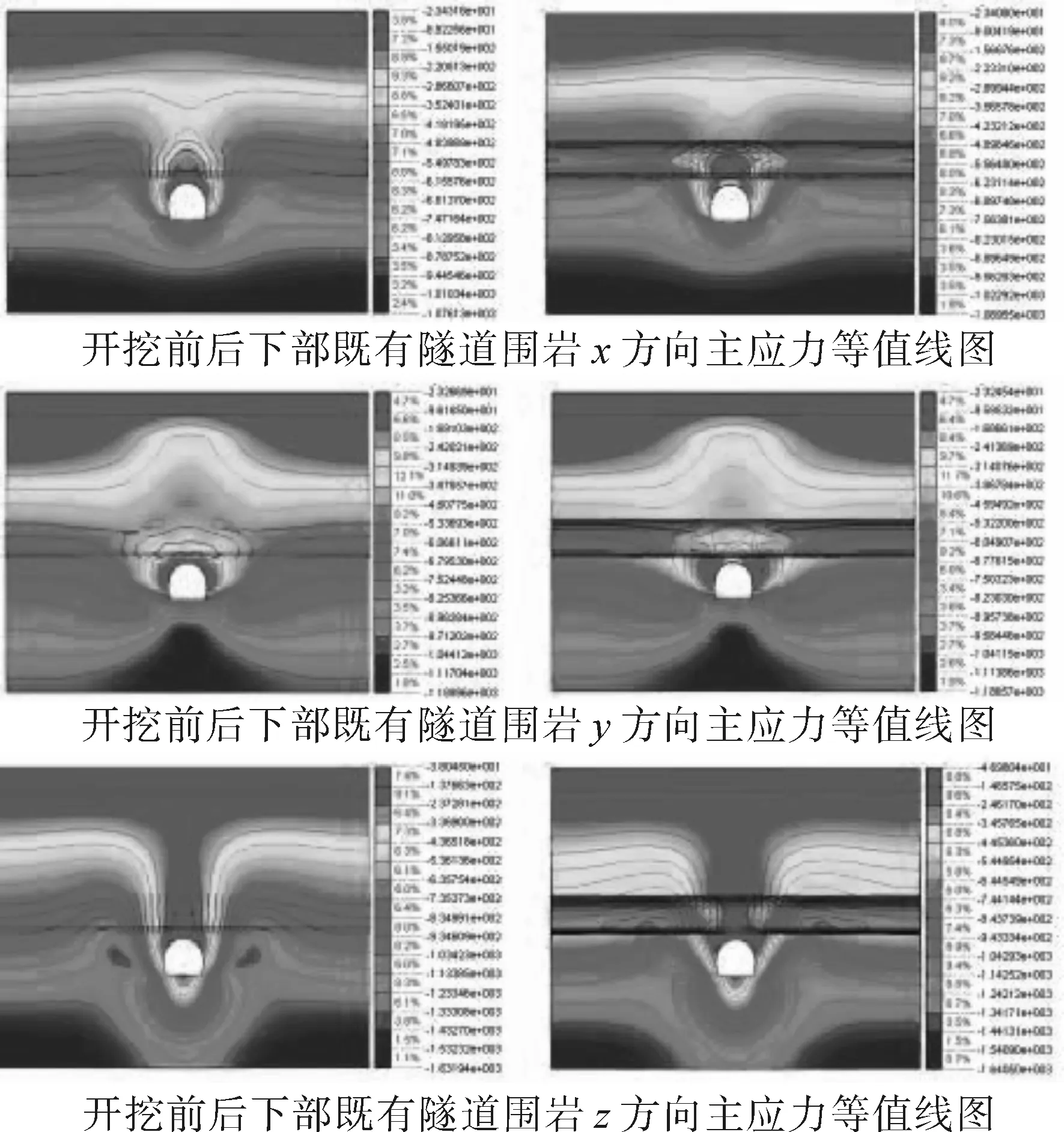
图2 新建隧道开挖前后下部既有隧道围岩x、y、z方向主应力等值线图

从图2可以看出，“上穿”新建隧道开挖前，围岩内各方向均受压应力；“上穿”隧道开挖后空间交错部位各方向主应力发生如下变化。

方向围岩应力呈现不同程度变化，其中拱顶位置的应力变大，拱肩位置应力略有变大，拱腰和拱脚应力基本没变；方向围岩应力除拱脚位置压应力有一定增加外，其余位置基本均无变化，但拱顶及拱肩应力分布范围受上隧道开挖影响变化明显；方向拱顶、拱肩、拱腰、拱脚位置围岩压应力均略有变大，但拱顶的压应力值分布范围由于受上隧道开挖的影响变化明显。

2.2.6 3组小鼠用力最大呼气流速比较 对照组和脂多糖组在6、18、36 h后的用力最大呼气流速比较，差异无统计学意义(P>0.05)。18、36 h后，甲强龙组用力最大呼气流速较脂多糖组升高，差异有统计学意义(P<0.05)；6 h后，两组用力最大呼气流速比较，差异无统计学意义(P>0.05)。

隧道开挖前后下部既有隧道围岩最大、最小主应力及剪应力等值线图，具体如图3所示。

从图3可以看出，“上穿”新建隧道开挖前后，围岩最大主应力沿隧道开挖断面均表现为压应力，开挖后既有隧道围岩中拱顶、拱肩、拱腰、拱脚各处压应力大小基本无变化；但拱顶、拱肩及拱腰位置压应力的分布范围变化明显，这是由于上部隧道的开挖围岩压力得到一定释放，导致靠近新建隧道位置围岩应力减小。最小主应力开挖前后也都是压应力，最大值有一定变大，在交错部位分布范围变化与最大主应力变化类似，并且沿隧道轴向的分布范围表现出在交错部位比较集中，在交错范围外分布较小。

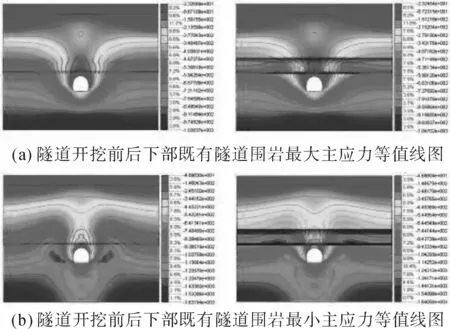
图3 隧道开挖前后下部既有隧道围岩最大、最小主应力及剪应力等值线图

“上穿”隧道开挖前，既有隧道围岩中剪应力值较小；开挖后，剪应力值有一定增加，并且拱顶处剪应力为零。剪应力在整个既有隧道沿轴向的分布范围表现出在交错范围外既有隧道左拱脚和右拱肩受拉剪应力；左拱肩和右拱脚受压剪应力，且交叉范围内剪应力值减小。

3.2 不同交错竖距对下部既有隧道围岩应力变化影响分析

通过建模将“上穿”隧道各主应力及剪应力在拱顶、拱肩、拱腰、拱脚位置各工况开挖前后的应力值做差，并与开挖前的应力值相比求得各点应力值在其开挖前后的变化率，绘制变化率曲线图，结果如图4、图5所示。

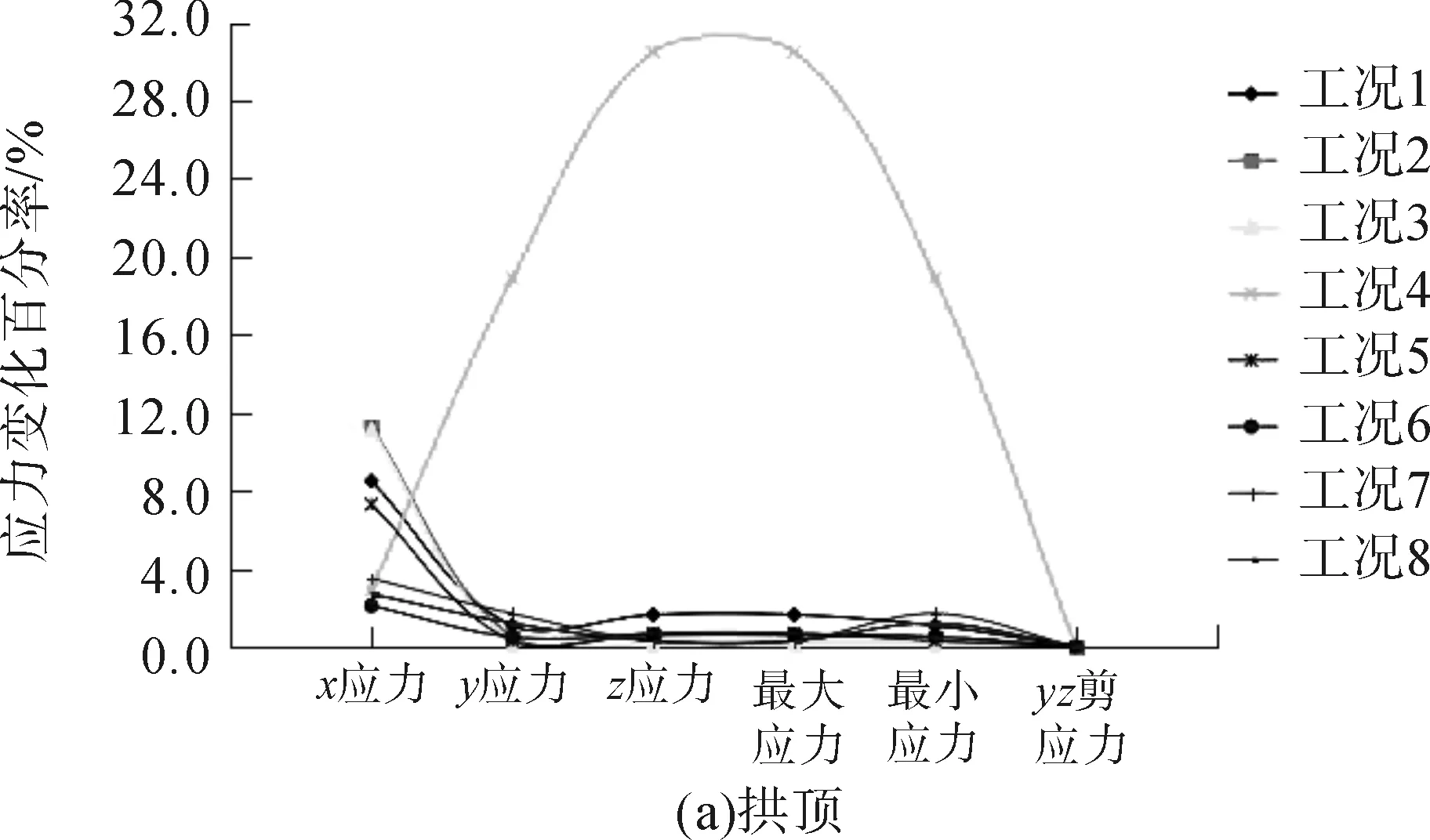
图4 拱顶、拱肩位置各应力在不同工况下开挖前后应力变化率曲线图

从图2～图5可知，“上穿”新建隧道开挖前后，由于卸荷作用，下部既有隧道的拱顶位置应力变化率最大;其次是拱肩、拱腰位置。拱脚位置的应力变化率最小。

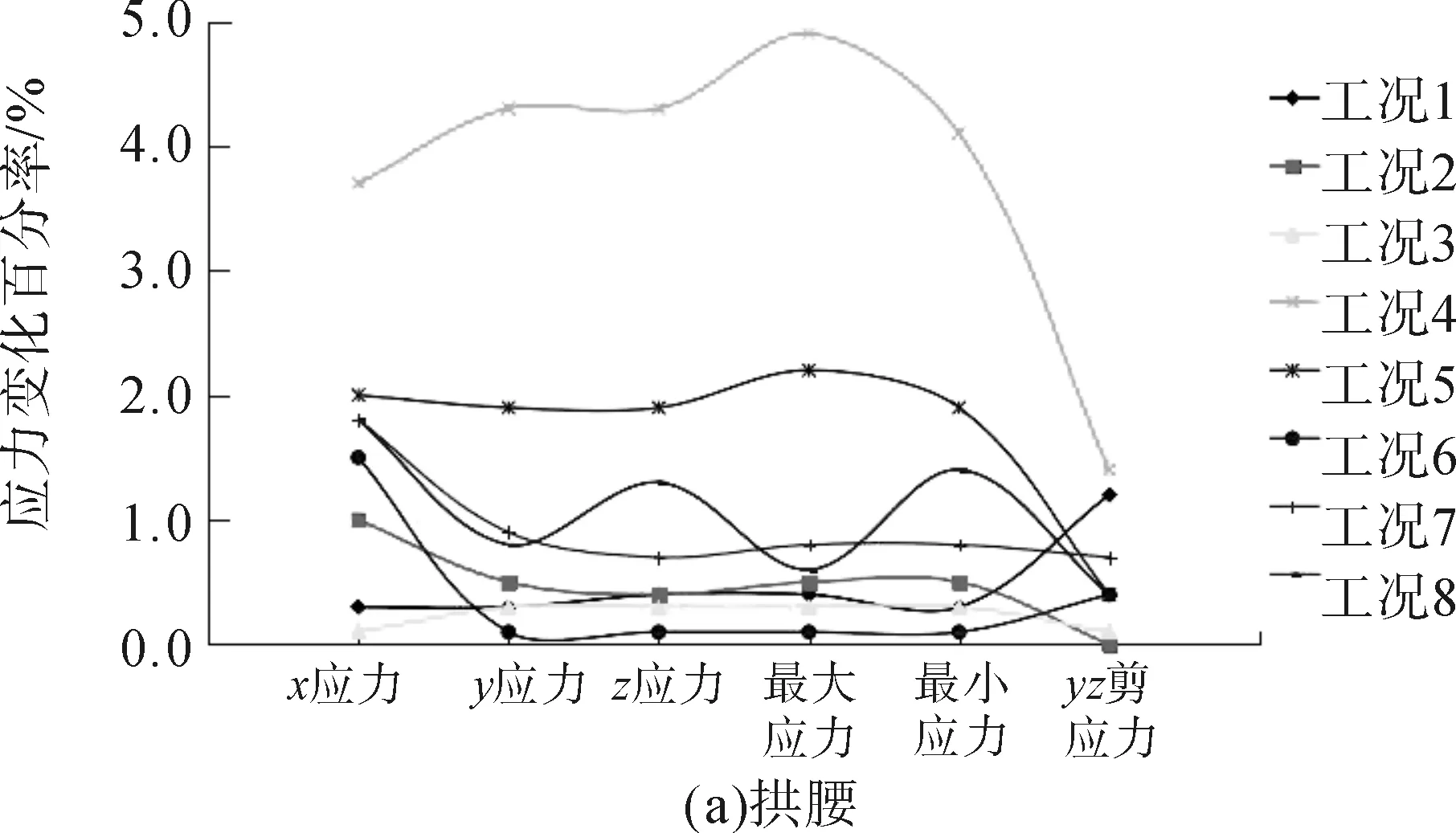
图5 拱腰、拱脚位置各应力在不同工况下开挖前后应力变化率曲线图

结合本文实际依托工程地质状况，在工况4时，“上穿”新建隧道的开挖对下部既有隧道拱顶位置和拱腰位置应力的影响最大；在工况3时，“上穿”新建隧道的开挖对下部既有隧道拱肩位置各应力的影响最大；在工况1、工况2开挖时会对围岩应力变化产生较大影响，即交错竖距在上部新建隧道0.5倍洞跨内时，上部新建隧道开挖对下部既有隧道围岩应力影响最大。

在工况5、工况6开挖时对围岩应力变化产生较大影响，即交错竖距在上部新建隧道0.5～1.5倍洞跨时，上部新建隧道开挖对下部既有隧道围岩应力影响较大。

在工况7、工况8开挖时对围岩应力变化影响均较小，即交错竖距在上部新建隧道1.5倍洞跨外时，上部新建隧道开挖对下部既有隧道围岩应力影响较小。

4 “上穿”新建隧道围岩应力特征分析

为便于分析新建隧道围岩应力的变化，在分析下部既有隧道时，同样取一些代表断面及应力变化比较稳定的关键点来研究。“上穿”新建隧道分别以空间交错竖距：1、2、3、5、7、10、15和20 m这8种工况从既有隧道上方正交穿过。

图6 新建隧道围岩各应力沿轴向等值线图

从图6可以看出，由于下部既有隧道的存在，上部隧道开挖后各应力分布跟单个隧道开挖或远离交错位置的端头位置相比都发生了明显变化。为了进一步研究在不同竖距开挖对新建隧道围岩应力的影响，根据新建隧道在8种工况中交错位置中心点处断面上的拱顶、拱肩、拱腰、拱脚、拱底等关键点应力大小分别制成8种工况对应的各关键点位置应力的发展变化曲线图，具体如图7～图9所示。

从图6～图9可以看出，下部既有隧道对新开挖的“上穿”新建隧道各方向主应力均有影响，并且呈现出对拱脚、仰拱底位置影响较大；拱肩、拱顶位置影响相对较小。

结合图7～图9可以看出，工况1～工况3的、、方向主应力及最大、最小主应力基本都呈现先增大后减小且应力值最大情况，说明在交错竖距1～3 m时“上穿”新建隧道围岩应力受下部既有隧道影响较大，即交错竖距在上部新建隧道0.3倍洞跨内时，下部既有隧道对上部新建隧道开挖围岩应力影响最大。

(a)x方向

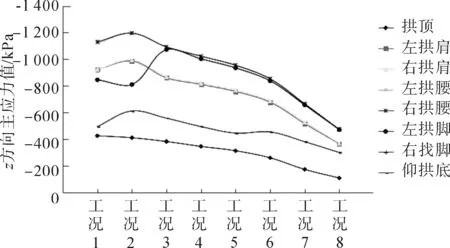
图8 新建隧道围岩z方向主应力、最大主应力在不同竖距下的变化曲线

图9 新建隧道围岩最小主应力及xz方向剪应力在不同竖距下的变化曲线

从工况3～工况8的、、方向主应力及最大、最小主应力基本都呈现出迅速减小且到工况8各应力值大小趋于接近，说明在交错竖距3～20 m内“上穿”新建隧道围岩应力受下部既有隧道影响迅速变小，并且在20 m时接近无影响范围，即交错竖距在上部新建隧道0.3～2倍洞跨内时，“上穿”新建隧道围岩应力受下部既有隧道影响迅速变小，并且在上部新建隧道2倍洞跨内时接近无影响范围。

面上剪应力分布表现出左拱肩和右拱脚为压剪应力，右拱肩和左拱脚表现出拉剪应力，并且拱肩、腰位置剪应力受交错竖距影响较大，拱顶和仰拱底位置剪应力受交错竖距影响较小；并随交错竖距从1 m增加到20 m，下部既有隧道对“上穿”新建隧道的剪应力影响减弱，各位置剪应力均趋于零。

5 粘接锚杆作用机理

早期隧道围岩加固的锚杆大都属于端头锚固型，其锚杆端部会产生应力集中现象，并且锚杆的杆体大部分外露，容易被锈蚀，很难满足有永久支护需求的隧道工程。为了解决上述问题，全长粘接型锚杆应运而生并得以发展。

全长粘接型锚杆是指用胶粘材料(如各种胶粘树脂材料、水泥砂浆等)将锚杆杆体的全长与其周围围岩体有效粘接起来，使锚杆的全段都能提供锚固力，从而很好地提高了锚杆对围岩的加固效果。这类锚杆的变形刚度比端头锚固型锚杆大很多，当隧道岩体沿着全长粘接型锚杆的任意部位变形，该型锚杆都能提供较好的约束作用，并且锚杆全段都被胶粘材料所包裹，能起到防锈蚀作用，更适合作为永久支护结构使用。因此，全长粘接型锚杆在隧道工程中的使用越来越广泛。

5.1 锚杆杆体与胶粘材料之间的作用机理

锚杆与胶粘材料间的粘接力主要包含以下几个方面：

(1)化学粘接力：锚杆表面与胶粘材料之间的胶力是锚杆提供给发生剪切作用的围岩的基本抗力，但当锚杆与隧道围岩间发生相对滑移后，这种粘接力就消失了；

(2)机械咬合力:由于锚杆表面存在肋节、螺纹、皱曲等构造，使得锚杆与胶粘材料间产生了机械咬合力，当围岩发生剪切作用时机械咬合力与粘接力一起产生抗力，发挥稳定围岩的作用；

(3)摩阻力:由于锚杆和胶粘材料在围岩内是通过化学作用粘接结合在一起的，但隧道围岩的变形，会对锚杆系统产生一定的挤压作用，使其形成与锚杆表面摩擦系数有关的摩阻力。并且，锚杆与胶粘材料间的挤压力越大，接触面的粗糙度越高，这种摩阻力也会越大。

5.2 胶粘材料与围岩体之间的作用机理

胶粘材料与隧道围岩间的作用力大小取决于：胶粘材料与围岩体的接触面积、胶粘材料的粘接强度、锚杆孔壁的粗糙度与清洁度等因素。这些影响因素主要通过对围岩与胶粘材料之间粘接力和摩擦力的大小来影响粘接围岩与胶粘材料之间的应力。围岩与胶粘材料间的粘接力主要受锚杆孔周围围岩强度和粘接材料本身强度的影响；而摩擦力的大小则主要与孔壁的径向压力、锚杆孔粗糙度等因素有关。因此，当胶粘材料与锚杆孔壁的摩阻力小于胶粘材料对锚杆的握裹力时，锚杆的支护性能就取决于锚杆孔壁围岩与粘接材料间的最大摩擦力。

6 结语

通过对贵州省某机场高速夏家岩隧道“上穿”贵昆铁路塔山脚隧道8种不同竖距下的建模分析得到以下结论:

(1)“上穿”新建隧道开挖前后，由于卸荷作用对下部既有隧道的拱顶位置各向应力影响最大，其次是拱肩、拱腰位置，对拱脚位置的应力影响最小。因此建议施工过程中加强对下部既有隧道的监测尤其是拱顶位置；下部既有隧道对新开挖的“上穿”新建隧道各方向主应力均有影响，并且呈现出对拱脚、仰拱底位置影响大，拱肩、拱顶位置影响相对较弱，建议设计中增加交错位置仰拱及拱脚位置的配筋；

(2)结合本文实际依托工程地质状况，交错竖距在上部新建隧道0.5倍洞跨内时，上部新建隧道开挖对下部既有隧道围岩应力影响最大；交错竖距在上部新建隧道0.5～1.5倍洞跨内时，上部新建隧道开挖对下部既有隧道围岩应力影响较大；交错竖距在上部新建隧道1.5倍洞跨外时，上部新建隧道开挖对下部既有隧道围岩应力影响较小；

(3)结合本文实际依托工程地质状况，交错竖距在上部新建隧道0.3倍洞跨内时，下部既有隧道对上部新建隧道开挖围岩应力影响最大；交错竖距在上部新建隧道0.3～2倍洞跨内时，“上穿”新建隧道围岩应力受下部既有隧道影响迅速变小，并且交错竖距在2倍洞跨左右时接近无影响范围；

(4)全长粘接型锚杆的作用机理：锚杆与胶粘材料间的粘接力主要包含化学粘接力、机械咬合力、摩阻力等；胶粘材料与围岩之间的影响因素主要为胶粘材料与围岩体的接触面积、胶粘材料的粘接强度、锚杆孔壁的粗糙度与清洁度等其主要通过对围岩与胶粘材料之间粘接力和摩擦力的大小来影响粘接围岩与胶粘材料之间的应力。