深度学习背景下的微专题教学设计
——以“比较大小”的微专题教学为例
尤 宁
(浙江省杭州外国语学校,310023)
深度学习是学生源于自身内部动机的、对有价值的学习内容而展开的完整、准确、丰富、深刻的学习,是一种有意义的、理解性的和阶梯式的学习.G·波利亚曾经指出:“良好的组织使得所提供的知识容易用上,这甚至可能比知识的广泛更重要.”依托主题明确、针对性极强的“微专题”进行复习,可以促进学生深度学习,从而有利于学生获得清晰的数学知识网络、系统的数学研究方法,加深对数学的理解,提高自身的数学素养.
高三复习不只是对已有知识的再回顾,或对基础知识进行机械记忆和堆砌,或对基本技能进行反复练习,更应该是对知识系统的再建构、再完善.复习阶段的练习并不在于“范广量多”,而在于“精准典型”.应通过精心设计的问题链和学习任务,引发学生深度思考,体会数学思维,积累解题经验.本文以“比较大小”为例,对利用微专题复习,促进深度学习进行探究.
一、微专题与深度学习的契合
微专题的设计是落实深度学习的重要支点.深度学习的发生需要整体把握核心内容,并且凸显学科内容本质[1].因此,微专题成为深度学习的主要抓手,体现数学核心知识之间的联系、特别是蕴含在核心内容中数学思想方法的联系,最终落实在以综合运用知识解决实践性、挑战性问题,进而发展问题解决能力为目标.“微专题”通常是指围绕复习的重点和关键点设计的、利用具有紧密相关性的知识或方法形成的专项研究,或者结合学生的疑点和易错点整合的、能够在短时间内专门解决的问题集.
深度学习要求学生在学习过程中真实地投入思维、情感、意志、价值观,发挥学生的主观能动性,因此,要遵循学生的认知发展水平.微专题的产生以及选题的过程需要考虑学生的需求,通过学生的反馈,了解他们感觉到的重难点和易错点,包括选题的环节也可以让学生参与进来.还要根据学生的学情,特别是学生需要突破的基础知识、基本题型、常用方法、数学思想等,设置具有针对性的“微专题”.通过这些“微专题”的复习,达到查找漏点、扫清盲点、厘清疑点、切实解决实际困难的目的.
深度学习要求学习内容尽可能规避零散的、繁杂的、无序的知识点,以构建学科核心知识结构,形成具有一定挑战性的、反映学科本质的教学主题.再次,深度学习应指向学科核心素养的培育.学科核心素养涵盖了学科知识、关键能力与学科思维.数学教育家波利亚曾说过:“一个专心的认真备课的教师能够拿出一个有意义的但又不复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”通过“微专题”复习促进学生深度学习,需要教师深入认识、解读数学的本质、本源,让学生通过学习逐步走近学科本质、了解学科本质、理解学科本质.复习时要围绕教材的主干内容、考试的重点及热点,设置一些对不同基础的学生都适用的“微专题”,通过这些“微专题”的复习,达到综合考点、把握重点、关注热点、切实提高解题能力的目的.
二、“比较大小”的微专题设计
题型1运用不等式的性质
例1下列命题为真命题的是( )

(B)若a>b>0,则ac2>bc2

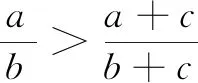
设计意图此类问题考查不等式的基本性质.源于课本,立足基础,对于基础知识全面考察,强调通性通法.
题型2运用函数的单调性
例2(2017年天津卷)已知奇函数f(x)在R上是增函数,g(x)=xf(x).若a=g(-log25.1),b=g(20.8),c=g(3),则a,b,c的大小关系为( )
(A)a (C)b 设计意图比较大小是高考的常见题型,指数式、对数式的大小比较要结合指数函数、对数函数,借助指数函数和对数函数的图象,利用函数的单调性、奇偶性等进行大小比较,要特别关注灵活利用函数的奇偶性和单调性、数形结合进行大小比较或解不等式. 题型3与基本不等式结合 例3(多选题)已知实数a,b满足a2-ab+b=0(a>1),下列结论中正确的是( ) (A)b≥4 (B) 2a+b≥8 设计意图涉及的知识点是通过基本不等式求出因式的最值或者证明不等式是否成立,要特别注意基本不等式等号成立的条件,多变量的情形应考虑转化为单变量,那样会简化运算. 题型4引入中介“桥梁” (A)a (C)b 设计意图此类问题往往涉及到与指数对数有关的比较大小,由于不同底,无法根据单调性等比较大小,但是可以判断此数与1或者0的大小,进而确定这些数的大小. 题型5构造函数 (A)a (C)b 设计意图构造辅助函数是一种常用的方法,解题中若遇到有关不等式问题,则应根据题目给出的形式构造对应的函数,或者通过适当的变形设法建立起目标函数,并确定变量的限制条件,通过研究函数的单调性,常可使问题变得简单明了. 题型6利用导数 例6(2021年全国乙卷)设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则( ) (A)a (C)ab 设计意图通过导数研究函数的单调性、最值、交点、零点等问题,对函数图象形成精准的认识与刻画,常可使问题变得清晰明了.同时也往往需要根据导函数的“形状”或变换不等式“形状”.对于多参数问题经常要与分类讨论相结合. 题型7综合应用 (1)设函数g(x)=xf(x)-x2,求函数g(x)的单调区间; (2)证明:ex-2xlnx-x>1(ln 2≈0.693,e≈2.718). 设计意图本题需综合应用各种数学知识,通过构造函数,研究导数的极值,并且在第(1)小问中得到线索,寻找到合适的桥梁,再通过反向演绎,提出猜想,给出逻辑严密的证明. 1.实时反馈,保证和彰显微专题效果 Eric Jensen和LeAnn Nick-elsen将深度学习定义为新内容或技能的获得必须经过一步以上的学习和多水平的分析或加工,学生可以通过改变思想、控制力或行为的方式来应用这些内容或技能[2].认知心理学的研究表明,对初次接触的复杂事物,大脑只能产生粗略的、非常不准确的表征,学习者在第一时间难以完成复杂学习,因此没有反馈几乎是不可能学会抽象的复杂的认知.反馈可极大地促进考核成绩的提高和直接迁移成绩的提升,同时作业反馈也是优质课堂活动的组成部分. 2.归纳与反思是深度学习发生的保障 深度学习的教学逻辑由学生认知序列、学科内容特征、学科核心素养、学习效果反思四个要素构成.深度学习依赖于对学习结果的反思,缺少反思的学习容易陷入浅层学习,反思在一定程度上保证深度学习的批判性、独立性与实践性.教师的关注点往往更多地落在学生是否解决问题,而疏于引导学生反思问题解决的过程.这种学习过程既不利于学生掌握解决问题的方法,也错失内化感悟新知的良机.弗赖登塔尔指出:“反思是数学思维活动的核心和动力”,因此,在高考复习教学过程中,应抓住时机,积极引导学生对所复习的对象进行回顾与反思,让学生经历数学知识“再发现”的过程,以促其对旧知产生新认识,助其对解题积累新经验,从而使学生在进一步完善自身认知结构、促进知识的同化与内化的同时,逐步形成数学的思维方式. 3.以生为师,推动学生实现深度学习 可以适时地尝试让学生学习老师的备课方式,在习题的讲解上做到易题拓展讲,难题分解讲,横向对比讲,纵向联系讲.这样有利于提升学生的兴趣和信心,开拓思路,提升学生的思维品质,培养探究能力.实现从“会做”到“会讲”,从“以为自己懂了”到“真的懂了”的跨越. 深度学习不是被动接受知识的灌输,在参与课程活动、对人类成果进行体验的过程中,要尽可能减少由过于追求知识本身而导致学生主观能动性被忽视的状况,避免让学生成为知识和技能的“搬运工”.深度学习强调引导学生积极探索、经历知识的形成过程,以知识体验为前提、以能力为中心建立学生与学习内容之间的紧密联系,精确地把握学科本质,提升学科核心素养. 总之,微专题教学在知识的整合和优化上有着得天独厚的优势,教师必须系统地把握教材,理解学生,注重联系,养成良好的教学思维习惯,更加高效地教学.微专题在教学过程中能有效地避免题海训练,注重数学思想的学习感悟,弥补传统教学的不足,发挥学生主体作用.合理设定微专题,恰当地选择学习策略,能高效地引领学生进行高效率的学习,长此以往,必将取得良好的长期效益.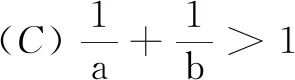
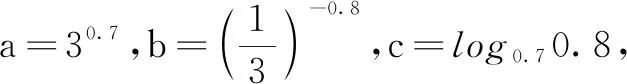
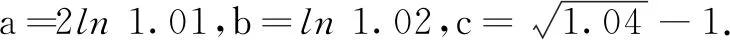
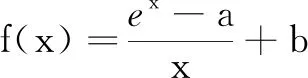
三、微专题设计评价

