体外预应力加固锚固装置设计与构造研究
任文辉
(中国铁建投资集团有限公司,北京 100855)
0 引言
为了施加可靠、有效的压应力,对结构采用预应力加固。作为一种主动加固法[1],预应力加固体系的重点在于预张力的合理设计、锚固及转向装置安全可靠。其中锚固体系不仅要承担预应力的传递,还需将产生的集中应力分散传递给锚下混凝土锚固装置[2]。预应力加固锚固体系主要由锚具、锚垫板、螺旋筋及锚固装置共同组成。
预应力加固桥梁体系中的锚固件是一种特殊构造。国内学者对锚固构造的研究主要聚焦于锚固装置局部承压设计、锚固构造配筋设计方法、钢-混剪力连接件、后锚固群锚设计等,如付星燃等[3]设计了高强耐候钢结构和超高性能混凝土(UHPC)锚固块。王艳武等[4]提出一种装配式锚固装置并进行实体有限元分析。
国内外学者对体外预应力混凝土梁锚固结构力学性能的研究取得了不少成果,但主要聚焦于锚固区计算设计方法方面,均偏理论计算,对实践的指导作用有限,同时针对加固方法、实际加固工程中锚固区其他合理构造的研究有所欠缺。本文将基于Midas FEA有限元分析对锚固装置构造进行优化,同时提出混凝土锚固装置配筋设计方法。
1 锚固装置特点
1.1 结构特点
锚固体系结构有以下特点:
(1)外加预应力结构力筋,特别是体外索加固完全依靠锚固装置锚固,一旦锚固装置破坏失效,导致的后果将是灾难性的。
(2)不同于新建结构,预应力加固体系中锚固装置属后加构造,锚固装置与原结构的有效连接将直接影响预应力加固效果,因此预应力结构的锚块与原结构连接设计必须进行严格周密的计算,以保证预应力加固结构的安全性和可靠性。
(3)不同于原预应力结构,预应力体外索的锚固较一般体内预应力索困难,如考虑到换索因素,钢索张拉后锚具后面不能用混凝土封闭,对于锚固区锚具块的防腐及耐久性应重点考虑和设计,并留有空间以放置千斤顶和便于钢索切断操作。
1.2 设计原则
(1)锚固结构应尽力使主梁受力明确。
(2)尽量减少体外预应力束预留构造对主梁削弱的影响。
(3)体外预应力结构在锚固区受到很大的局部压力,为了保证混凝土强度需要在锚固点和附近的桥面板,底板、腹板宜局部进行加固。
(4)锚块的尺寸应由锚具尺寸、锚具布置、张拉设备尺寸和局部承压要求来决定,必要时应加大锚块尺寸。
2 锚固装置构造优化
2.1 锚固区应力分布
体外预应力加固锚固区受力非常复杂,在巨大压应力作用及构造约束的影响下,锚固装置构造锚固面及与原结构约束边界常产生较大的拉应力,受预应力布置形式、原结构材质、局部尺寸及受力等因素影响,传统设计及配筋多集中在锚固构造本身,常忽略了锚固装置的设置及预应力施加后对原结构的影响。因此,设计时除防止锚固装置受压、剪切破坏外还应重点考虑采用预应力加固后如何减小对原结构受力的影响。
为了研究锚固装置的受力状态,采用Midas FEA建立有限元模型分析其锚固区应力分布情况。模型建立了某桥锚固构造(如图1所示),单侧腹板张拉共计2束10ϕs15.2mm体外索,张拉控制应力为0.65fpk=1209MPa,考虑结构受力的圣维南原理,有限元模型建立了8m长的梁段。

图1 锚固装置有限元模型
纵桥向最大拉应力出现在锚固装置与箱梁腹板交界处,数值为6.255MPa;横桥向最大拉应力出现在锚固装置下锚点内侧边缘,数值为6.088MPa;竖桥向最大拉应力出现在锚固装置上端靠近翼缘板处,数值为3.405MPa,三向压应力均集中在锚点位置。锚固区最大主拉应力为13.271MPa,位置出现在上下锚点与腹板交界处,锚后应力影响区域长度约为90cm。锚固区最大主应力云图见图2,纵桥向应力云图见图3。

图2 锚固区最大主应力云图
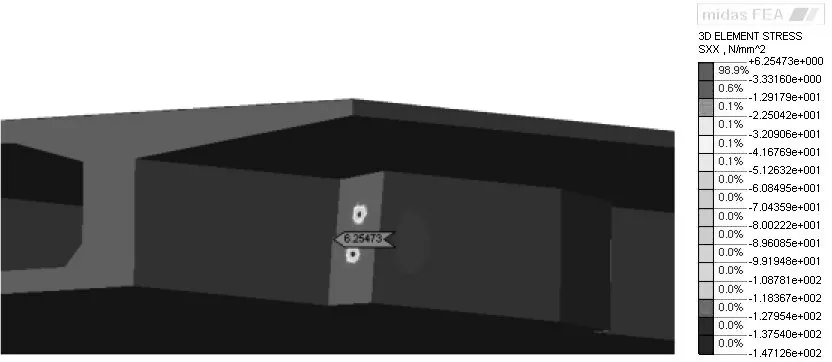
图3 锚固区纵桥向应力云图
以上计算结果表明,新增锚固装置与箱梁腹板交界处纵向拉应力及主拉应力较大,锚固装置的锚面上部及内侧拉应力较大,设计时必须考虑对拉应力较大区域采取措施,防止锚固装置受拉破坏
2.2 构造优化
根据上节计算结果,新增锚固装置与箱梁腹板交界处纵向拉应力及主拉应力较大,锚固装置锚面上部及内侧拉应力较大。考虑到钢材抗拉压承载能力较强,因此在锚固区设计时可增设局部钢构件以改善锚固装置的受力性能,形成钢-混锚固结构。锚固区新增钢构件示意图如图4所示,据此建立了相应的有限元模型。锚固区新增钢板等效应力云图见图5,锚固区优化前后应力对比见表1。
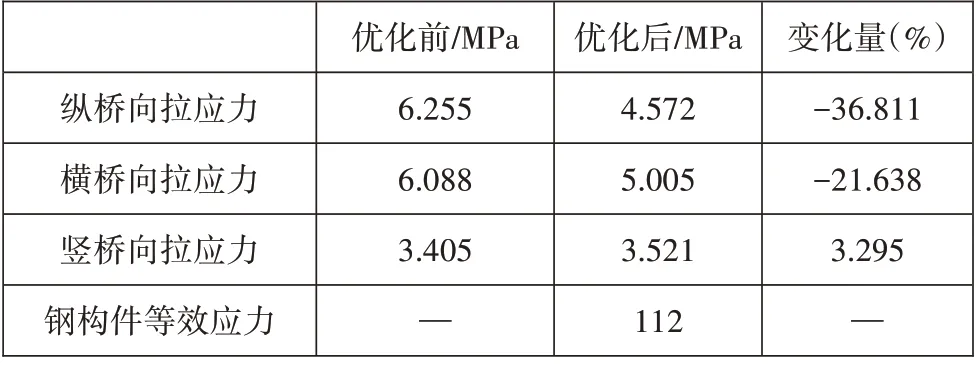
表1 (续)
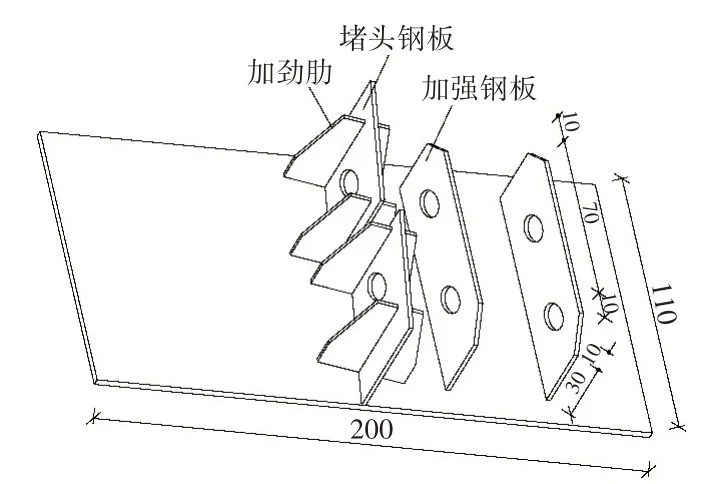
图4 锚固区新增钢构件示意图(单位:cm)

图5 锚固区新增钢板等效应力云图

表1 锚固区优化前后应力对比
由表1可知,锚固区设置条件有限,锚固装置尺寸大小设置受限,为有效降低局部应力集中现象,防止混凝土受拉开裂,在锚固区应力集中区域通过增加钢构件能有效改善锚固区及原梁受力性能,实际施工时也可在混凝土表面刻槽粘贴锚固钢板,并在条件允许的情况下尽量与原钢筋相连接。
3 混凝土锚固的配筋
锚固区内需设置用以抵抗横向拉力的锚下钢筋,一般由螺旋筋、封闭箍筋或两者共同组成,使锚下钢筋与锚固区混凝土共同工作,承受劈裂应力,控制局部裂缝,满足结构的使用要求。同时,在锚固区的锚具下应预埋钢垫板,并设置间接钢筋和附加钢筋。
针对锚固区受力特点及传统方法的局限性,将利用Midas FEA“局部方向内力总和”功能确定锚固区局部内力并进行配筋设计,结合规范验证实际工程中锚固区的配筋状况。
箱梁及锚固区局部构造如图6所示,锚固区预应力采用5ϕs15.2mm钢绞线,张拉控制应力为0.75fpk=1395MPa,原结构与锚固装置混凝土标号采用C40,弹性模量为3.15×104MPa,泊松比为0.2,有限元模型如图7所示。

图6 锚固区构造图(单位:cm)
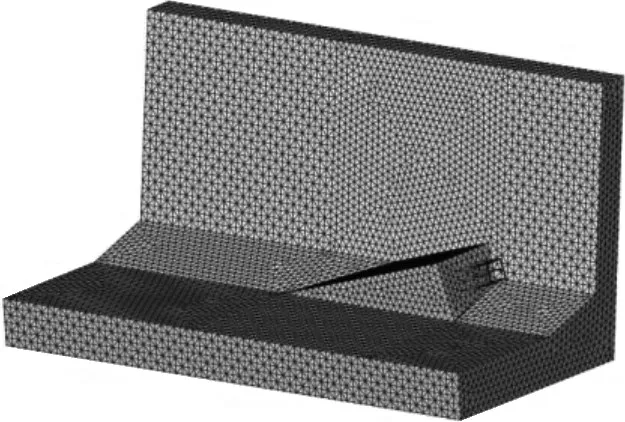
图7 锚固区有限元模型
纵桥向最大拉应力出现在锚固装置端面与箱梁底板倒角交界处,数值为2.296MPa;横桥向最大拉应力出现在锚固装置端部与箱梁腹板交界处,数值为0.819MPa;竖桥向最大拉应力位置基本与纵桥向最大拉应力位置相同,稍偏底板侧,数值为0.884MPa,三向压应力最大均集中在锚点位置。锚固区最大主拉应力为2.732MPa,位置与纵桥向最大拉应力位置相同,锚后应力影响区域长度约为60cm。锚固区最大主应力及纵向应力云图如图8、图9所示。

图8 锚固区最大主应力云图

图9 锚固区纵桥向应力云图
根据应力分析结果计算配筋,使用程序提供的“局部方向内力总和”功能,可以获得计算位置的剖面内力。
锚固区受力示意见图10所示,受力特点有:①锚固区背面Z方向上的剥离力T1;②锚固区背面Y方向上的破裂力T2;③锚固区前和箱梁混凝土翼缘上的张拉T3;④锚固区下部张拉T4;⑤因预应力偏心布置引起的弯矩张力T5;⑥预应力弯起位置张力T6。

图10 锚固区受力示意
锚固区配筋示意图如图11所示,其中F1为针对T1的配筋;F2为针对T2,T3的配筋;F3为针对T4,T5的配筋;F4为针对T6的配筋。

图11 锚固区配筋示意
按照本节所述方法,利用Midas FEA“局部方向内力总和”功能确定锚固区局部内力并进行配筋设计,指导了多座桥梁的加固工程,详见表2。

表2 理论计算配筋量和实桥配筋量比较
5 结语
预应力张拉后锚固构造区受力复杂,除直接承受巨大的压应力外,锚固构造与原结构约束界面常出现较大的拉应力及主拉应力,设计时必须考虑对拉应力较大区域采取措施,防止锚固装置受拉破坏,同时也需重视产生的拉应力对原结构局部区域的影响,必要时需对原结构局部进行加固。
对于锚固区配筋较为准确的方法是通过建立实体有限元模型确定应力并进行配筋,但应力需通过积分或建立拉-压杆模型进行拓扑优化转换为内力方可用于直接配筋。本文利用Midas FEA“局部方向内力总和”功能相对准确地得到了关键截面的内力,直接可以用于设计配筋,可大幅减少材料浪费,锚固区配筋合理,且经多个工程实践得以验证。

