桥梁损伤识别中的指标优化和机器学习应用研究

杨超，孙建朋，刘凯，邵永军，刘卫刚，刘亚红

（1.陕西高速公路工程试验检测有限公司，陕西 西安 710086；2.西安建筑科技大学，陕西 西安 710055）

0 引言

近年来，随着经济发展，交通基础建设长期处于高位水平，对安全性和时效性的要求也不断提高。桥梁作为可跨越河流、山谷等的路线构筑物，随着承载力和跨径的提升，其在路线中的占比也逐年攀升。据统计，仅2020 年我国新建公路桥梁就达7 700 座[1]，近年来的新建量甚至超过了以往的总和[2-3]，而这也意味着“老龄”桥梁数量的增长[4]。随着桥梁服役时间的累积，部分桥梁由于设计荷载考虑不足、施工缺陷、偶发事故等因素，致使其性能劣化加剧，出现了不同形式的损伤，而由上述原因导致的桥梁安全事故也时有发生，因此在新建的同时，也应重视桥梁的检测维护。

我国中小跨径桥梁占比较多，如果能考虑损伤随时间的发展，在其出现或发展的前期进行有效识别，明确损伤位置和程度，便可及时修复并制定合理的运营养护措施，进而抑制损伤发展，使得桥梁剩余寿命延长，同时间接降低事故发生率，因此损伤识别研究变得亟需。而早期为获取桥梁状态的有效信息，较依赖检测人员通过外观检查及试验结合经验做出判断，此类方法存在易受主观影响、时效性差、成本较高等弊端，已难以适应当前快速增长的任务量，因此积极快速的损伤识别方法研究尤为重要，国内外许多学者也据此做了大量研究[5-15]。

基于桥梁静动力特性的整体识别法可在一定程度上提高识别效率，并能改善以往方法中存在的不足，而频率和位移影响线作为可操作性较好且精度较高的参数，涉及研究也较多，但该类参数通常难以直接利用自身进行损伤信息表征，而需通过衍生变形或重构才能实现较好的识别效果。Cawley等[16]发现单处损伤位置可通过两阶频率变化比来表征；Bicanic 等[17]通过框架结构试验，也发现损伤与固有频率存在关系；王艺霖等[18]基于位移影响线的增量图差异实现损伤识别；孙珂[19]针对非理想支承条件下的梁式结构，提出基于对称测点的差值指标和基于平滑技术的曲率指标。在此基础上，有学者将机器学习方法与指标结合，以实现更高效的识别，Kirkegaard 等[20]以频率变化进行BP网络训练，并完成对钢梁的损伤识别；Kaminski[21]利用算法模型对自振频率、正则化的频率变化率进行了识别效果对比分析；孙宗光等[22]将频率和振型结合作为输入，也取得了较好的效果。

综上，频率和位移影响线是包含损伤信息的参数，但以往构建的指标中仍存在不足。由于多数桥梁具有对称性及频率改变的非唯一性，以往频率指标可能会造成对称损伤的误判，因此具有一定的局限性。另外，以往的位移影响线指标还存在难以有效表征损伤程度的问题。鉴于此，本文首先在以往研究的基础上进行两类参数指标的优化，并通过数值算例进行验证分析，最后结合两类机器学习算法探究智能识别模式。

1 指标构建

1.1 有载频率指标

桥梁属于多自由度体系，在移动荷载作用下考虑质量影响的自由振动方程可表示为：

式（1）中：K(p)为刚度矩阵；{ p}(nump × 1)为刚度未知参数，nump为数量；M(xi)为质量矩阵，xi(i=1,2,…,N+1)为移动荷载位置；ωi,j(j=1,2,3,…,numf)为移动荷载处于i 位置时结构第j 阶有载频率；{ }ϕi,j为相应的振型向量。而其无阻尼方程可表示为：

由上式可得，频率是受体系刚度和质量影响的全局参数，其可反映桥梁的整体性能变化。由于桥梁体系庞大，局部损伤主要表现在刚度下降，而对质量影响较小[20]，因此依托其关联性，可反演桥梁的损伤信息。

此处结合车桥耦合理论，利用移动质量荷载位置变量来使得损伤对频率的影响显性化，且由于该放大效应会随车辆位置的移动而发生变化，可避免以往频率指标识别中的对称性和非唯一性问题。该方法可描述为：首先在桥梁合理位置安装传感器采集频率数据，然后将桥梁划分为N个单元和N+1个节点，当移动荷载依次通过第i(i=1,2,…,N+1)个位置时，获取前m 阶有载频率数据，同样利用无损数值模型或新建桥梁获取该数据，最后利用损伤前后的数据进行参数指标构建，进而通过图像的趋势和异常位置来识别损伤。

假设桥梁无损状态下的有载频率数据为ωi,j;0(i =1,2,…,N + 1; j = 1,2,…,m)，而当前状态下为ωi,j(i =1,2,…,N + 1; j = 1,2,…,m)，利用这两组数据定义桥梁有载频率平方变化率参数指标，移动荷载位于i 处，桥梁损伤前后第j阶有载频率平方变化率可表示为：

考虑到当移动荷载位于振型节点时对频率的影响有限，因此为防止漏检情况出现，进一步将移动荷载处于同一位置时的前n阶SFFC进行求和，将其表示为：

1.2 位移影响线指标

此处以简支梁为例，只考虑小变形和线弹性阶段，由位移互等定理：

该位移通常包含线位移和角位移，此处仅针对竖向线位移进行讨论。位移影响线表征测点位移与荷载位置间的函数关系，因此求解某点的位移影响线可简化为移动荷载作用于测点求解梁上其他位置的位移表达式。受集中荷载作用，简支梁上某位置的位移可由单位荷载法求解，其中忽略轴力和剪力，可简化表示为：

其与损伤的关系，文献[23]中已有介绍，此处不再赘述。改进指标还需借助灰度分析理论实现，通过对灰度关联模型的改进，进一步完成参数指标的构建，可表示为：

2 SFCR数值算例效果分析

本文选用如图1所示的三跨连续梁桥对该指标进行验证分析。采用Euler-Bernoulli 梁单元，从左至右以0.1m 划分为100 个单元，编号为E1#～E100#，而节点编号为N1#～N101#，采用等截面箱梁形式，材料采用C50混 凝 土， 容 重γ = 25kN/m3， 弹 性 模 量E = 3.45×107kN/m2，泊松比μ = 0.2。依据Saint-Venant′s Principle 理论，局部损伤模拟采用调整材料弹性模量的方式实现，移动荷载为300kN，梁单元采用BEAM3单元。

图1 连续梁单元划分示意图

采用移动的MASS21 质量单元模拟移动荷载。通过绑定完成质量单元与梁单元的结合，在模态分析时，采用Block Lanczos特征值求解器计算移动荷载在不同位置的有载频率数据，计算仅在竖向平面内进行，忽略阻尼和温度的影响，且考虑到实际应用中高阶频率通常较难获取或误差较大，因此结合振型分析结果，此处仅利用前四阶竖弯频率进行指标参数的计算分析。

在完成模型建立后，还需进行损伤工况的模拟设置，由于设置工况较多，此处仅列出四种工况进行分析，具体工况如表1所示。

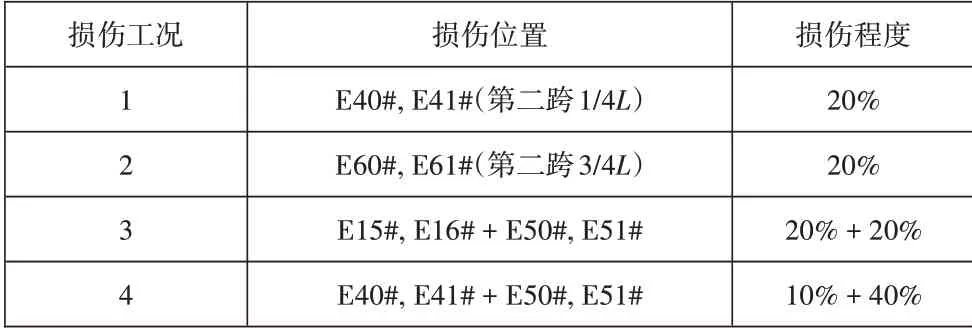
表1 连续梁损伤工况

进一步依据指标计算方法获取各损伤工况下的参数值并进行归一化处理，结果如图2所示。

图2 不同损伤工况下的SFCR参数值

由工况1 和工况2 单位值损伤下的识别结果可看出，SFCR 能有效识别出桥梁的损伤位置，未损伤处的图像基本保持稳定的小幅度波动状态，而损伤处均产生了明显的突变，同时验证了该指标能有效避免对称损伤频率变化的非唯一性限制。

工况3 和工况4 为两处损伤下的识别结果，可以看出SFCR 图像仍可准确识别出损伤工况中的每一个损伤位置，且当损伤程度不同时，图像峰值也存在显著差异，损伤大的更容易被识别，而小损伤则可能被大损伤所掩盖。综合模拟结果表明：SFCR 参数指标能有效进行桥梁损伤定位。

3 IGCC数值模拟分析

对于利用灰度分析方法构建的位移影响线指标IGCC 的验证分析，本文利用跨径为20m 的等截面预应力简支箱梁实现。以1m 为一个单元长度，从左至右共划分为20 个单元和21 个节点，预应力钢束选用钢绞线1860，其余参数同上个模型，且由于该指标需验证对于损伤程度的识别效果，因此在损伤程度范围变化中以5%进行分级设置，由于工况设置较多，此处仅给出如表2所示的4种工况。

表2 简支梁损伤工况

完成模型的建立和损伤工况设置后，提取跨中节点位移影响线数据，并计算各对应位置参数指标，其中单处损伤和多处损伤识别结果分别如图3、图4所示。

由工况5 和工况6 识别结果分析可得，无论损伤位置处于跨中或1/4 跨，对于损伤前后的指标计算结果，图像在损伤位置均产生了突变，且随着该位置损伤程度的增大，指标系数会降低。通过该点系数的值，可对损伤程度实现一定误差范围的表征，且当损伤程度在10%～30%范围时，该指标的表征精度更高。通过其他工况的试算发现，当损伤程度较小时，该指标的敏感性会降低，并可能伴随对损伤位置的误判；当损伤较严重时，该指标对损伤位置的表征愈发明显，但损伤程度的识别精度会受影响，并可能导致图像上其他位置的波动性增强。

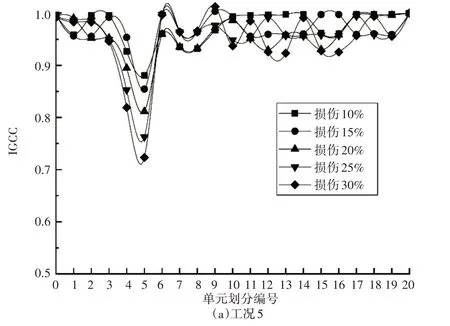
图3 单处损伤工况下的IGCC参数值

而单从损伤程度的表征来看，该指标对于远离跨中测点的损伤表征中，当损伤在20%范围内时，其存在一定的放大现象，而对超过20%的具有一定的削弱效应；而对于靠近测点位置的损伤，损伤程度表征在两种情况下均呈现出一定的放大效应，该现象与测点影响线分布规律有关，但总体而言，该指标对涉及的单损伤工况仍具有较好的识别效果。

多处损伤工况下的IGCC 参数见图4。由多处损伤识别结果可得，对于两处对称位置的损伤，当损伤程度不一致时，对损伤较大位置的抑制效应相对明显，而小损伤位置受影响相对较小。通过试算，当两处损伤程度一致或接近时，移动荷载施加在该位置，造成的位移影响线的异常改变基本一致，因此损伤程度识别误差相对较小，且由于对称损伤会引起整体趋势的变化，也在一定程度上提高了该位置的关联性，使得识别到的程度偏小。即使面对复杂的三处损伤工况，该指标对应的参数图像仍可有效标定损伤位置，且各损伤处对应由系数表征的损伤程度也基本吻合。当损伤处于对称位置且损伤程度一致时，各位置的损伤程度表征误差将会受到抑制，使得精度有所提高。综上，IGCC 指标同样具有较好的损伤定位能力，且可对损伤程度实现一定误差范围的表征。

4 SFCR损伤定位抗噪性分析

虽然SFCR 指标已通过数值算例得到了较好的验证效果，但考虑到实际应用中可能存在的噪音干扰，而在噪音影响下仍能利用指标进行有效的识别是更具实际价值的。以往研究表明，损伤识别结合机器学习的智能识别模式，可提高识别的效率和精度[21-22]，因此利用机器学习中的堆栈降噪自动编码机，通过将加噪的识别参数作为堆栈降噪自动编码机网络的输入，可进一步进行降噪和识别，以此对损伤定位的抗噪性进行分析。采用Tensorflow 平台构建网络模型，该网络模型具有3个DAE隐藏层和1个分类层，分类器采用Softmax回归模型。

图4 多处损伤工况下的IGCC参数值

此处主要选取单损伤工况进行定位抗噪性分析，其中无监督训练采用随机生成的600个单损伤指标参数样本实现，而监督训练采用每跨4等分处损伤对应的指标参数实现，监督训练样本共有9种损伤工况，每种工况涵盖7%～50%内的9 个程度，添加10%～80%服从Guass 分布的随机噪音形成独立的训练和测试集，网络的配置为[101,200,100,50,9]，位置标记采用One-Hot 编码。在测试的同时，结合BP网络进行对比分析。

最终测试效果主要从准确率和置信度两方面进行评价，而SDAE-Softmax 和BP 网络测试的准确率随噪音程度变化曲线如图5所示。

由图5 可看出，当噪音低于50%时，BP 网络和SDAE-Softmax 定位准确率趋势基本一致；而当超过50%后，BP 网络准确率下降较SDAE-Softmax 更为显著；当噪音达到80%时，SDAE-Softmax 准确率仍有56.17%，高出BP 网络22.21%。由此可看出，SDAESoftmax在高噪音下具有一定的优势。

图5 不同噪音程度下的损伤定位准确率

进一步选取各跨跨中损伤工况下含50%范围内噪音的SFCR 进行分析，通过对比BP 网络和SDAE-Softmax的输出置信度来分析其降噪性能，其10次测试的平均置信度如图6所示。

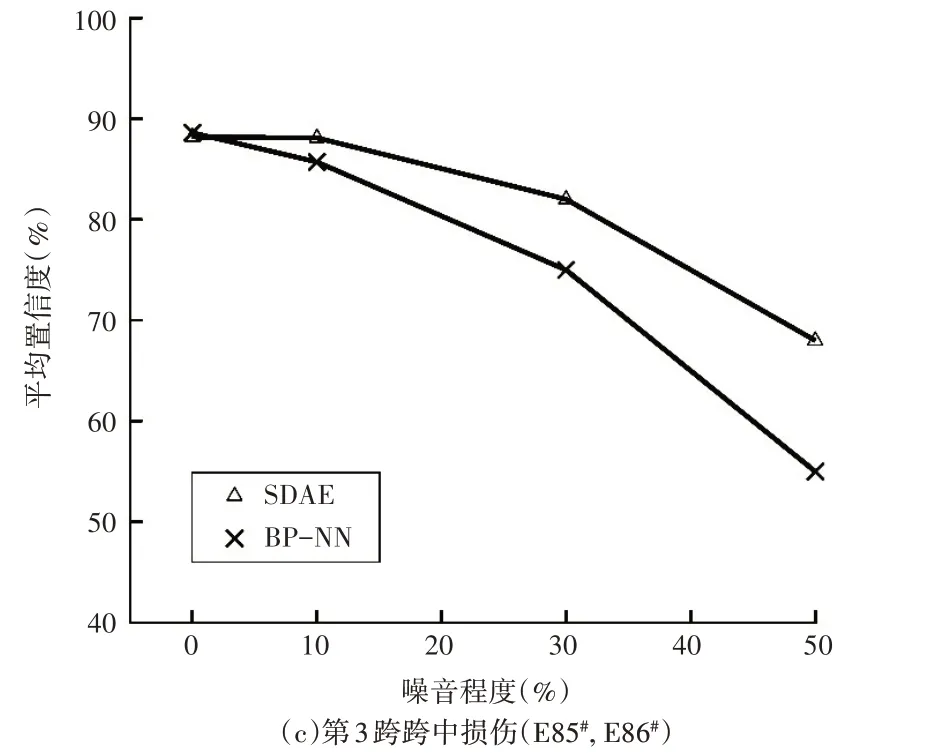
图6 连续梁不同位置损伤置信度随噪音程度变化曲线

由图6可看出，SDAE-Softmax 置信度高于BP网络，虽然随着噪音程度的上升，两类网络的置信度均有下降，但SDAE-Softmax 的下降幅度小于BP 网络。综合两种评价结果表明，SDAE-Softmax 引入的降噪手段可有效提高参数指标识别的抗噪性能。

5 IGCC结合BP的识别效果研究

由于机器学习具有较强的非线性映射能力，能更好地提取关键特征，因此尝试利用BP算法结合IGCC指标数据探究识别效果，以期弱化原始指标存在的波动效应，并改善原始指标对部分工况损伤程度表征精度不足的问题，同时进一步提升识别效率。此处共提取46组数据，然后通过重构方式扩容至966组，再对全部样本进行随机划分，将其中80%作为训练集，剩余20%作为验证集。

由于每组数据需识别两层特征信息，因此对于模型搭建，如果同时处理定位和损伤程度判断，则可能导致嵌套增多，出现耦合的概率变大，从而导致运行效率降低；且由于是同时完成，缺少中间的判断过程，最终也可能存在较大的误差风险。基于上述原因，此处采取分步实现的策略，先进行损伤位置的分类识别，进一步完成程度的回归拟合，而分类模型效果评价采用f1-score 指标，回归模型采用MAE（平均绝对误差）进行效果评价，其中分类和回归模型前两层均采用relu激活函数来进行映射输出。分类模型最后一层由于需进行离散输出，因此选择softmax 作为激活函数，而回归模型由于输出为连续变量，未设置激活函数。通过多次的调试训练，其最终训练迭代效果如图7所示。

由图7 可看出分类模型训练误差呈不断下降趋势，而精度不断上升，在经过500次迭代后，分类模型已经收敛，在训练集上的精度接近95%，而误差接近0.1，但受模型结构影响，后期参数更新过程中波动较为明显。而回归模型训练误差MAE 同样呈下降趋势，在接近第10 次迭代后趋于稳定，后续呈缓慢下降趋势，收敛性较好，最后训练误差基本稳定在0.07左右。

图7 BP分类和回归模型误差迭代趋势图

搭建的两类模型经过多次训练后，误差均已稳定在合理范围内，进一步结合两类模型进行验证，对随机划分的验证数据进行分类预测，其f1-score 为0.738，虽与训练时相比有所降低，但也体现出模型已形成较好的推测能力，总体而言能较好地完成损伤定位，且其召回率始终保持在较高水平。而回归计算的MAE 为0.092，与训练时的最终迭代误差相比有所增加，但对于所划分的验证集，其平均绝对误差也处于较小的范围内。

6 结论

本文以损伤识别问题中的指标优化和机器学习应用为主要研究内容，通过对频率和位移影响线两类参数进行指标改进，并在此过程尝试结合两类算法进行验证分析，获得的主要结论如下：

（1）SFCR 指标由于引入移动质量荷载，具有一定的“类时频域”特性，克服了对称结构频率变化的非唯一性限制；而IGCC 综合考虑了不同量纲下的趋势变化，具有较好的动态适用性，因此能更好地进行损伤定位，且可对损伤程度实现一定误差范围的表征。

（2）利用SFCR 分析数据结合构建的堆栈降噪自动编码机网络模型，可增强指标参数的表达能力，并提高识别时的准确率和抗噪性。

（3）构建的BP网络模型结合IGCC指标数据进行训练，可形成较好的推测能力，能弱化原始指标数据中的波动效应，并能改善部分工况损伤程度表征精度不足的问题。