瞬态过程中闸阀的流场温场及形变分析

王　冰，郭　赟,*，辛素芳，任春明，彭　倩，毕树茂

瞬态过程中闸阀的流场温场及形变分析

王冰1，郭赟1,*，辛素芳2，任春明2，彭倩2，毕树茂2

（1. 中国科学技术大学，核科学与技术学院，安徽 合肥 230000；2. 中国核动力研究设计院，四川 成都 610041）

闸阀是反应堆一回路系统的重要部件，瞬态过程中流体温场的变化会影响阀体的温场变化，进而影响阀门的密封情况。本文使用计算流体动力学方法对包含部分管路系统的闸阀进行瞬态三维流固耦合分析。通过对闸阀内流体的流场和温场的模拟计算，获得了瞬态过程中闸阀阀体温场的变化以及由于温场变化导致的热变形和热应力；在此基础上对不同边界条件和不同阀门结构进行了计算分析和评价，其结果可供闸阀设计参考。

闸阀；热应力；计算流体动力学

闸阀作为反应堆一回路中的重要设备，在某些瞬态过程中会经受温度和流量的迅速变化，从而产生额外的热应力。这会影响闸阀的密封性，因此需要对瞬态过程中闸阀内的三维流场和温场进行分析，确定瞬态过程中闸阀内温场的变化，以及由于温场变化导致的阀体变形情况。

国内的科研工作者对这类阀门的安全性和密封性等开展了相关的研究。秦武[1]等对核阀的使用现状及其主要特点进行了介绍，并指出了国内阀门现存的不足。熊冬庆等[2]对核电厂主蒸汽隔离阀的研制难点进行了分析。王湘江等[3]针对我国现有核阀不足，提出了一种新型谐波螺旋式阀门设计。赵英博等[4]对高温锻钢闸阀的温度场和应力场进行了分析。目前对闸阀的分析主要是稳态分析，随着研发要求的提高，闸阀在一些瞬态过程中的温场和形变的变化也需要在设计中明确，这就需要开展相应的瞬态分析。

采用数值方法，可以获得闸阀内部的流动和传热细节，以及阀体的应力场和形变场。本文采用CFD计算软件ANSYS Fluent 18，对包含部分管路系统的闸阀进行流动和传热的稳态和瞬态分析，得到了流场和温场，并在此基础上分析闸阀主体密封结构的形变程度。基于本文提出的方法，对闸阀在不同边界条件，以及不同几何结构条件下的计算结果进行了深入分析。

1　物理模型

1.1　湍流模型

标准模型是CFD中模拟湍流时均流动特性的最常用模型。标准模型可以在较少的计算资源下获得相对准确的结果，故可以对大尺度的工程问题进行数值模拟，被广泛应用于工程流动分析中。

标准模型允许求解两个独立的输运方程来确定湍流长度和时间尺度，关于和的守恒方程如下：

闸阀的上部腔室流速较慢，所以用湍流模型描述是不准确的，在研究的初期也考虑过使用分区模型来计算。使用分区模型存在两个问题，一是无法准确确定层流和湍流的分界位置，二是使用分区模型收敛性较差，无法达到收敛标准。湍流模型可能会增强换热，但是对于本研究来说增强换热是相对保守的，闸阀上部腔室也采用湍流模型是可以接受的。

由于阀体结构的复杂性，譬如在进入阀体后的连续突扩突缩流动以及通过阀板和阀体之间进入阀体上腔室内的狭缝流动，以及在瞬态过程中来流速度的变化，均会使得流动极为复杂，所以在一定的网格下使用时均模型时，无法得到普适的壁面函数，所以对于近壁区域需要做出一定的妥协，使用尺度化的壁面函数来求解边界层。近壁区域中的网格分辨率可以用*来表征，*是距壁面的无量纲距离。对于尺度化的壁面函数方法，*建议在11.225和300之间，在具体算例中已经通过优化网格使得尽量不触及这一区间的上下限。

1.2　边界条件和求解方法

研究对象为高温高压闸阀，闸阀的几何结构如图1（b）所示，一回路管道直径为300 mm，闸阀内部流道直径为250 mm，所以在进入闸阀前需要由渐缩管连接，支管直径为100 mm。闸阀的宽度为400 mm，高度为1 000 mm，闸阀上腔室宽度为300 mm。

计算区域如图1（a）所示，进出口边界为速度入口和压力出口。闸阀由阀体和内部流体区域组成。阀体的内壁面和流道的边界都被定义为无滑移的壁面。所有流道的热边界定义为绝热，闸阀的外表面也定义为绝热条件，以计算热应力的变化程度。阀体和内部流体之间的交界面定义为耦合壁面以进行温度数据的交换。

通过使用用户定义函数的功能（UDF），入口温度和速度被定义为与时间相关的函数。系统压力为15 MPa，平均温度为579 K。由于温度变化范围不大，因此根据压力将粘性，密度和热导率等物理量近似设置为常数。

图1　计算区域及边界示意图

采用有限体积法离散控制方程，差分格式选择二阶迎风，使用典型的SIMPLE算法进行求解。收敛标准为连续性残差小于1.0×10-5。对于瞬态计算的时间步长设置，在入口1的速度迅速变化的3 s内时间步长设置为0.002 s，其余为0.02 s。在每个时间步长内可以在不超过100次迭代下达到收敛标准。

计算环境为32核AMD处理器，128GB内存，Window10操作系统，完成一个典型瞬态算例约需1周时间。

1.3　网格及其独立性验证

使用软件UG NX 12.0进行几何建模。如图 2 所示，除了上腔室外，大部分流道采用结构六面体网格划分，闸阀阀体和上腔室采用非结构化四面体网格划分。边界层的网格被加密以满足*的要求。图3显示了*的分布，99%的壁面网格*达到了要求。因此，*最小值限制的影响基本上可以忽略不计，所以近壁网格是合理的。

为了验证网格独立性，选取网格数目分别为120万（粗糙网格），260万（基准网格），和400万（加密网格）的三套网格进行网格独立性验证。当流体流入闸阀的内部时流道突然扩张，下腔室内产生回流，此时流场相当复杂，所以选择阀体中心横截面的水平中心线（垂直于流动方向）的速度分布进行比较。图4所示为三套网格的计算结果中所选参考线的速度分布。根据比较结果，基准网格（260万）可以满足计算要求。

图2　闸阀网格示意图

图3　壁面分布

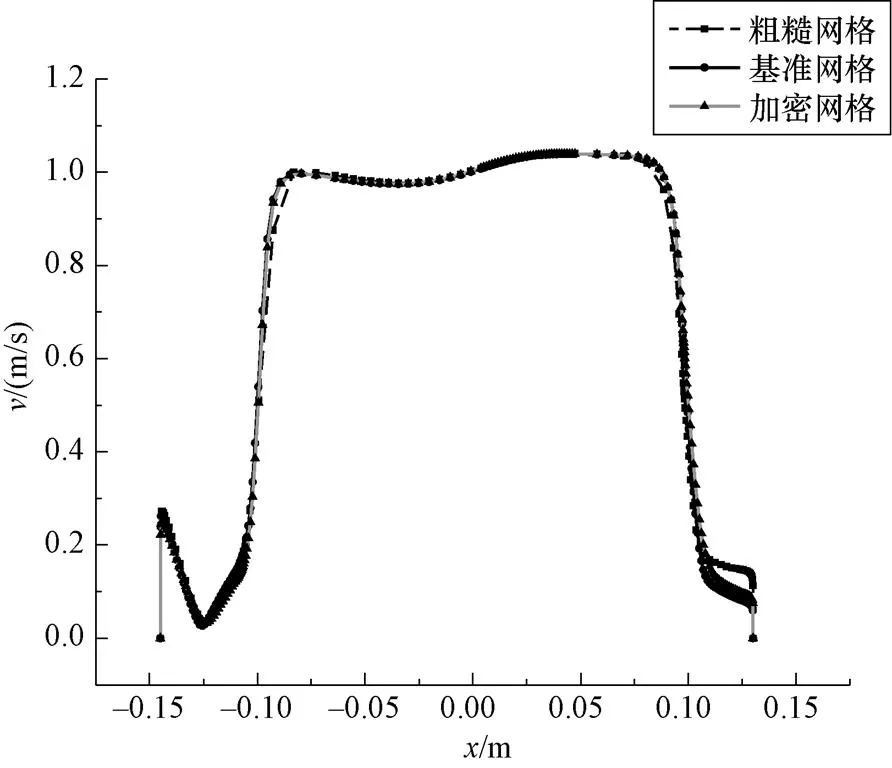
图4　参考线的速度分布比较

2　结果和讨论

2.1　闸阀内流场的稳态分析

闸阀内的流场是研究的重点，稳态分析结果作为瞬态分析的初始条件，得到闸阀内准确的稳态流场结果至关重要。阀体内部的流体区域可以视为突扩和突缩的组合，并且变化距离非常短，类似于不平滑变化的喷嘴结构。

2.1.1流场分析

图5显示了主流和截面的流场云图。沿主流方向中部在未进入阀体前为普通的管内流动，当流体流入阀体后，在截面的左右两侧观察到两个流向涡，在截面下方也可以观察到流向涡。可以理解为在进入突扩后，流体撞击对面的壁面，从而逆流形成涡流。这种现象可以在参考文献[5]中得到证实。闸阀的上腔室内以及阀板运动的区域内的流动都非常缓慢，流速均小于0.1 m/s，但值得注意的是在通往上部腔室的狭缝处的流速还比较大。综上所述，定性来看本文的计算是合理正确的。

图5　闸阀XY截面和YZ截面流场

2.1.2二次流流场分析

由于涡流和二次流对温场或热量的传递有很大的影响，所以下面对阀门内的二次流进行分析。

雷诺应力模型是目前最好的时均模型，它能够充分反映雷诺应力的各向异性，因此可以更准确地捕捉二次流流场。图6（a）所示为标准模型的计算结果，图6（b）为雷诺应力模型的计算结果，两者的中心区域均有一个大涡流，壁面边界附近有许多小涡流。相较于标准模型，雷诺应力模型对于靠近壁面的涡流捕捉更细致。总体来说二次流的流动相似，所以使用标准模型的计算可以反映该系统中流动的典型特征，并且相比RSM模型大大节约了计算量，这一点在后续瞬态计算中有重要意义。

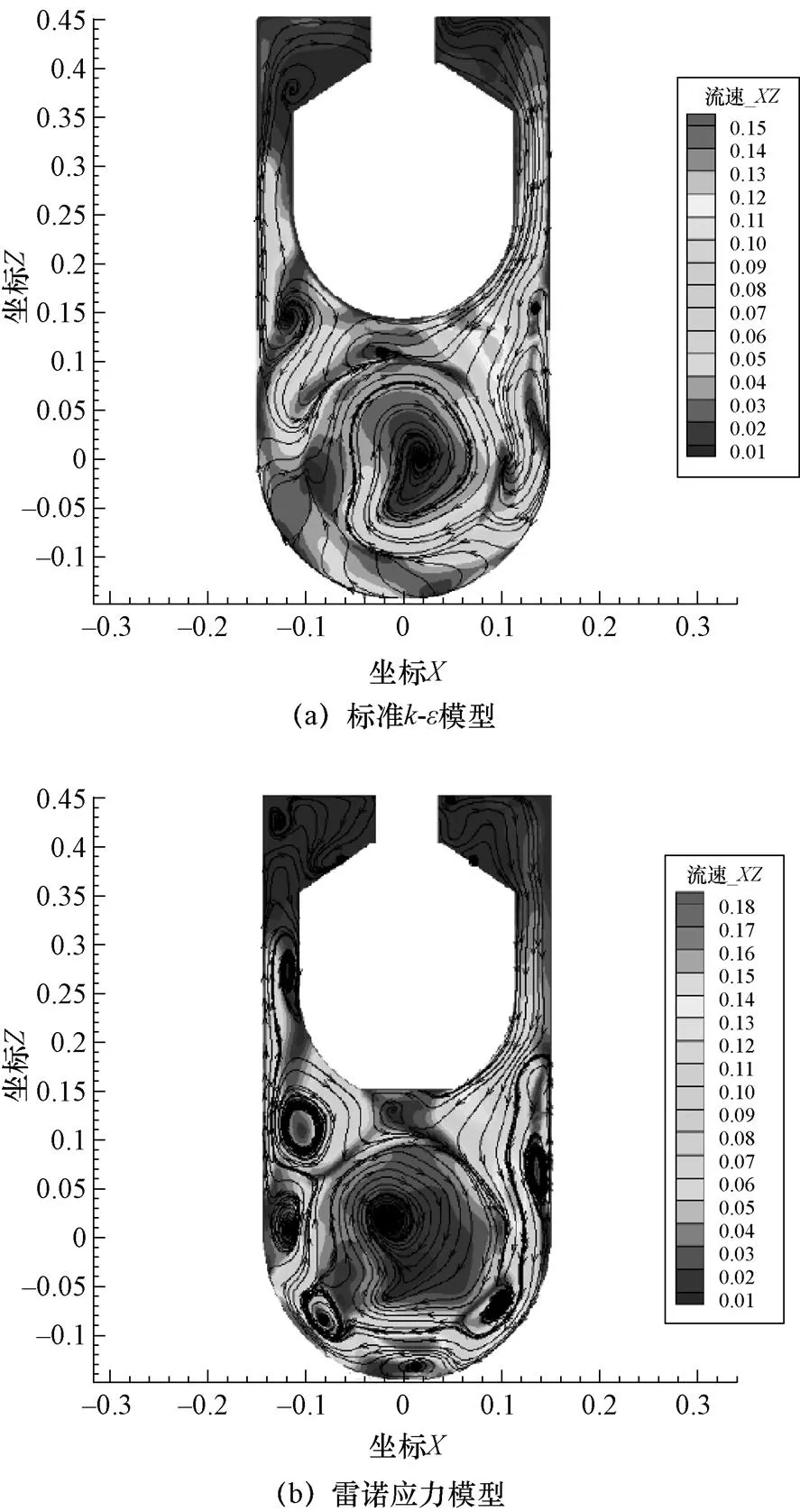
图6　闸阀内二次流流场

2.2　闸阀内流场温场的瞬态分析

本节对瞬态过程中闸阀内的流场和温场变化进行了分析，瞬态计算得到的不同时刻的温度分布是分析闸阀热应力和形变的基础。稳态时主管道内的流速为0.7 m/s，入口温度为591.5 K。在瞬态过程中，主管道的流速在10～13 s内迅速线性增大至3.6 m/s，随后在13～40 s内减小至3.2 m/s并不再变化；主管道内流体的温度在10～50 s内线性下降了55 K，随后在50～80 s上升至546.5 K，在80 s后保持为546.5 K。而支管仅在0～40 s注入热流体，支管流速为3.5 m/s，流体温度为591.5 K。瞬态过程中流量的增加和温度的降低会对闸阀产生冷却作用，闸阀内的温度会降低，并使闸阀的温度分布更加不均匀，和产生附加的热应力和形变。

在瞬态过程中，闸阀内的流场同稳态基本相似。随着主管道流速的增加，二次流流场整体强度显著增强，由厘米量级增加到了米量级，这会增强同阀体的换热，同时也使得更多流体进入阀体上腔室，同上部阀体进行换热。

闸阀受到主流的冷却温度逐渐下降，图7所示为150 s时闸阀截面的温度分布。

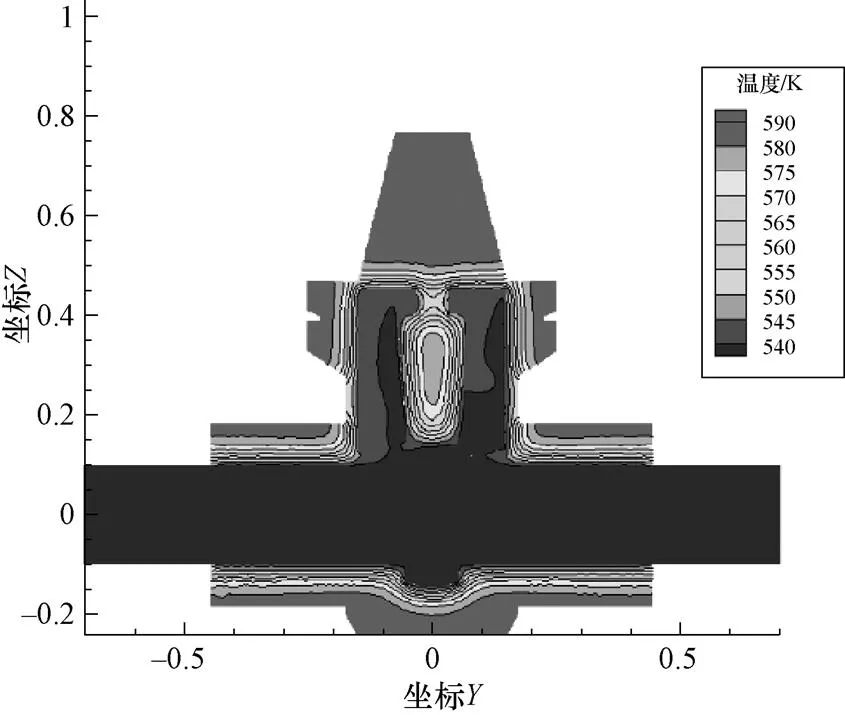
图7　150 s时闸阀内的温度分布

图8所示为监测点和监测线的选取。监测线选取为阀盖与阀体的分界面左侧截面的水平线，监测点选取为参考线上距离内壁面10 mm的位置。图9（a）所示为监测线在0 s，50 s，100～150 s时的温度分布。从图中可以看出，在外壁面绝热条件下，短时间内流体对闸阀的冷却作用只影响到了靠近闸阀内壁面的区域，而接近外壁面的区域温度变化较小。图9（b）所示为瞬态过程中监测点的温度变化。监测点的温度在20～80 s内下降较快，随后温度下降的速率逐渐减缓。150 s时监测点的温度为562.42 K，相较于稳态温度下降了29.08 K。

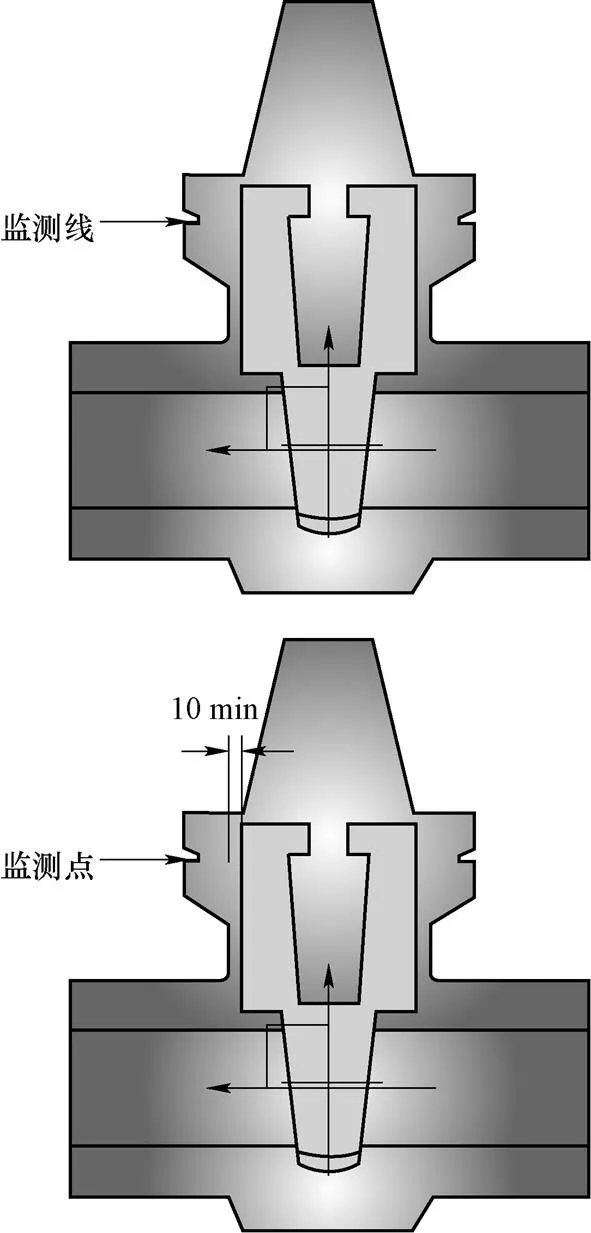
图8　闸阀内监测线和监测点的选取

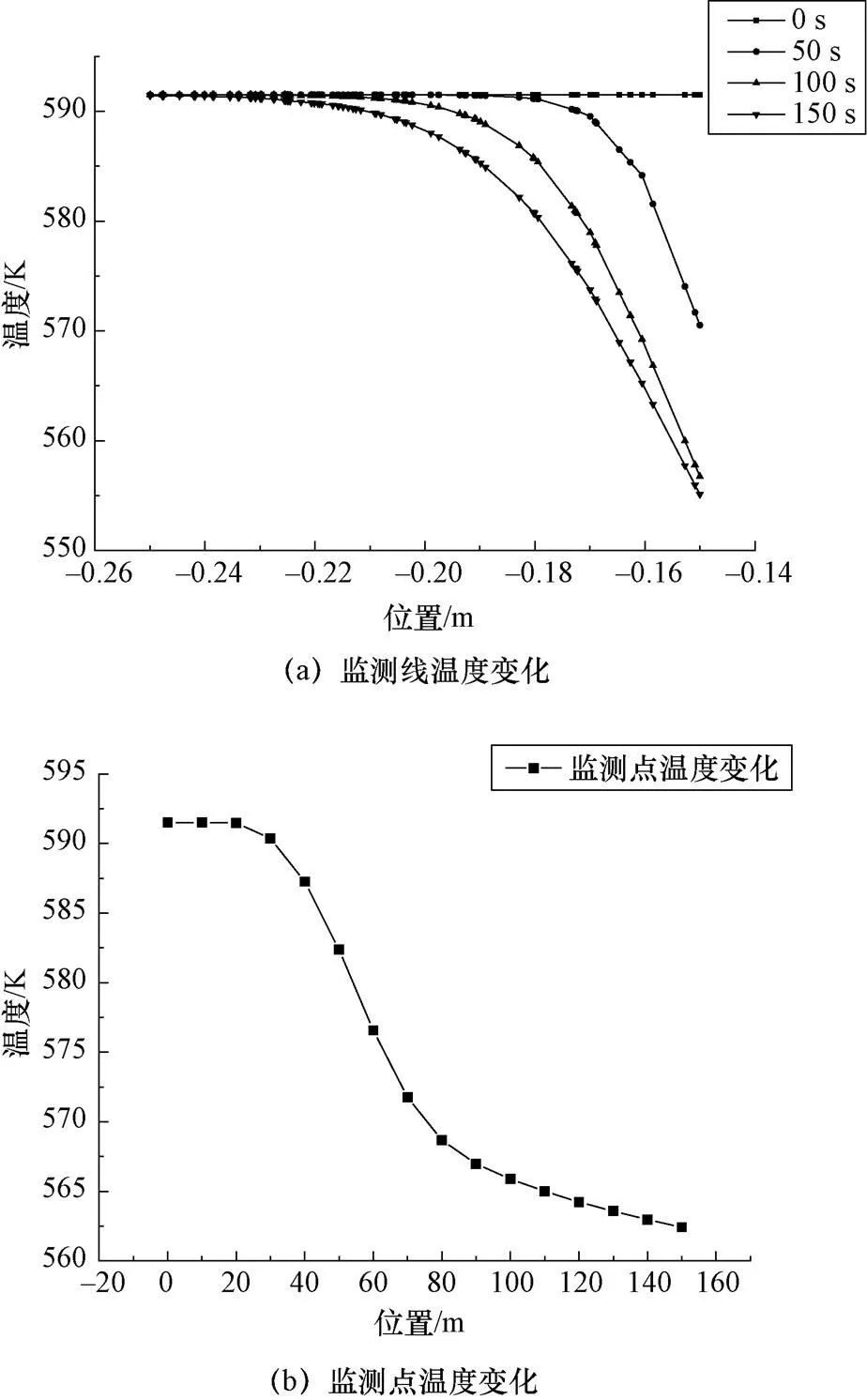
图9　监测线和监测点温度变化

图10所示为瞬态过程中闸阀最低温度和平均温度的变化。在瞬态过程中，闸阀的最低温度迅速下降，随后略微上升并趋于稳定，闸阀的最低温度为540.32 K，相应的最大温差为51.18 K；闸阀的平均温度缓慢下降，在150 s时，闸阀的平均温度为581.02 K，平均温度下降了10.48 K。

图10　闸阀的最低温度和平均温度变化

2.3　闸阀内的热应力和形变分析

闸阀的材料为304不锈钢，由于温度变化范围不大，所以不锈钢的物性近似设置为平均温度时的常数，物性参数如表1所示。如图1（b）所示闸阀的两端给定固定约束，参考温度设定为591.5 K。稳态计算时闸阀内为均匀的温度场，所以稳态时闸阀内的热应力和形变均为0。以下热应力和形变分析的结果均为瞬态过程中相对于稳态时的温度变化引起的热应力和形变。在热应力和形变分析中，选取瞬态计算中每间隔十秒的数据进行分析。

表1　不锈钢物性参数

图11（a）所示为150 s时闸阀截面的热应力分布。闸阀内部直接与流体换热的壁面处热应力较大。在瞬态过程中闸阀产生的附加热应力最大达到了246.46 MPa，位于上腔室与闸阀内部流道的连接处附近的壁面。图11（a）所示为150 s时闸阀截面的形变分布。闸阀的中上部形变较大。形变最大达到了0.242 mm，位于闸阀的阀盖，在闸阀的中部也产生了一处形变较大的区域，越接近闸阀的阀盖处形变越大。

图12所示为闸阀内的最大热应力和最大形变随时间变化。闸阀内的最大热应力在前70 s内迅速增大，随后逐渐趋于一个定值；在150 s时，闸阀内的最大热应力达到了246.46 MPa。闸阀内的最大形变随时间逐渐增大，但是增加的速率逐渐减缓，在150 s时，闸阀内的最大形变达到了0.242 mm。

图11　150 s时闸阀内的热应力和形变分布

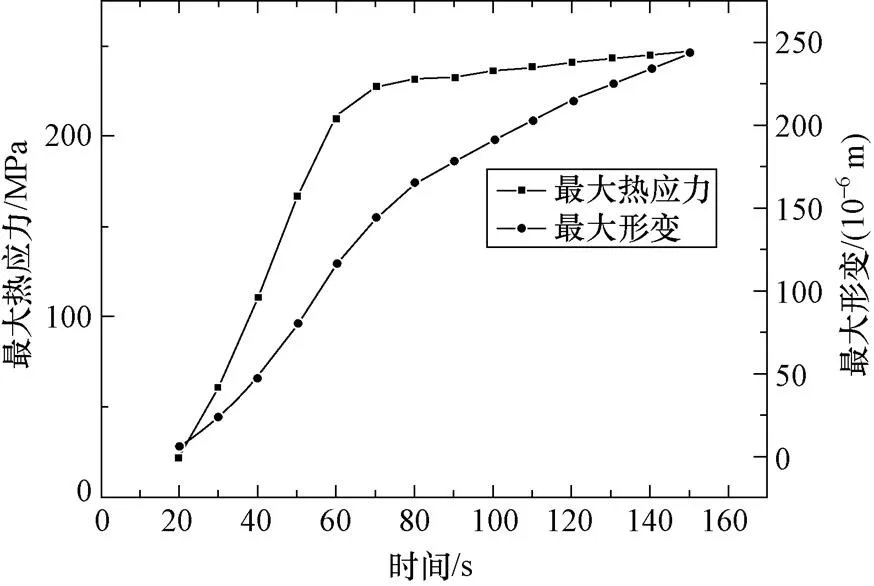
图12　闸阀内的最大热应力和最大形变变化

2.4　闸阀几何结构影响分析

基于上述计算结果，对主闸阀和流道的结构提出了改善结构，将连接上腔室和闸阀内部流道的狭缝由160 mm缩小为100 mm。物理模型和其他边界条件的设定均与2.2节相同。

图13所示为改善后的闸阀和原型在瞬态过程中的平均温度变化规律。缩小连接上腔室和闸阀内部流道的狭缝可以减弱上腔室的流动和换热，所以平均温度的下降更加缓慢。150 s时，原型的温度下降了10.47 K，而改变结构后的闸阀的温度下降了9.45 K，闸阀的温度变化减小了9.7%。

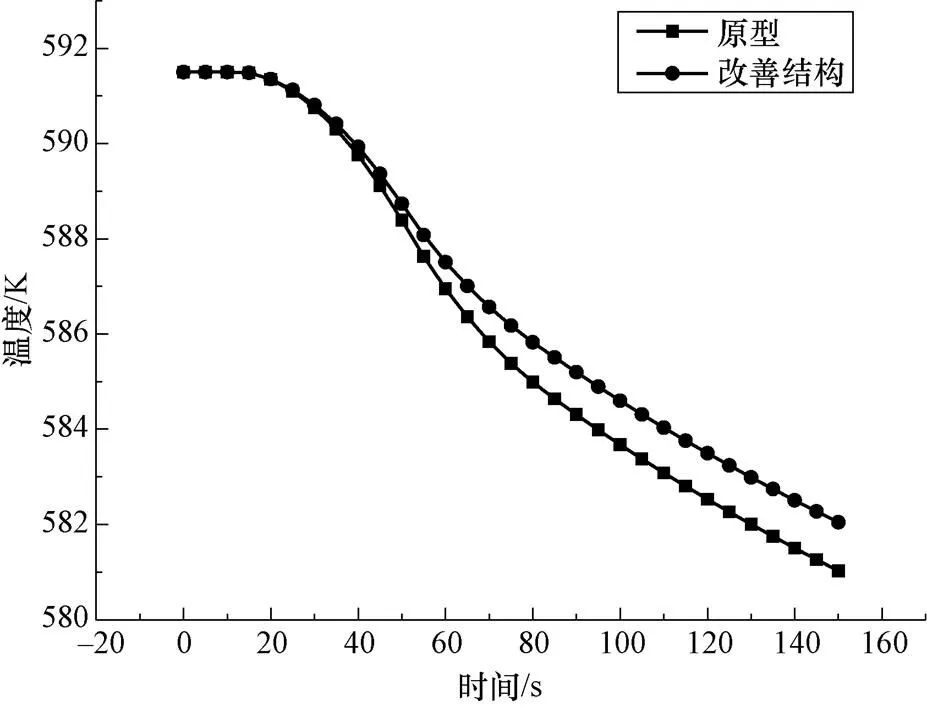
图13　闸阀平均温度随时间变化

2.5　闸阀外表面边界条件的影响分析

在瞬态计算中闸阀外表面的热边界条件近似设定为了绝热，在本节中将闸阀外表面的边界条件设定为自然对流边界条件，换热系数近似设定为10 W/（m2·K）。物理模型和其他边界条件的设定均与2.2节相同。

图14所示为150 s时闸阀内的温度分布，闸阀的阀盖处温度最低，闸板中心温度最高。

图15（a）所示为监测线的温度分布变化，与绝热的边界条件类似，流体对闸阀的冷却作用只影响到了闸阀接近内壁面的区域。图15（b）所示为监测点的温度变化，监测点的温度在150 s时下降了24.12 K，相较于绝热边界条件温度下降减少了4.96 K。

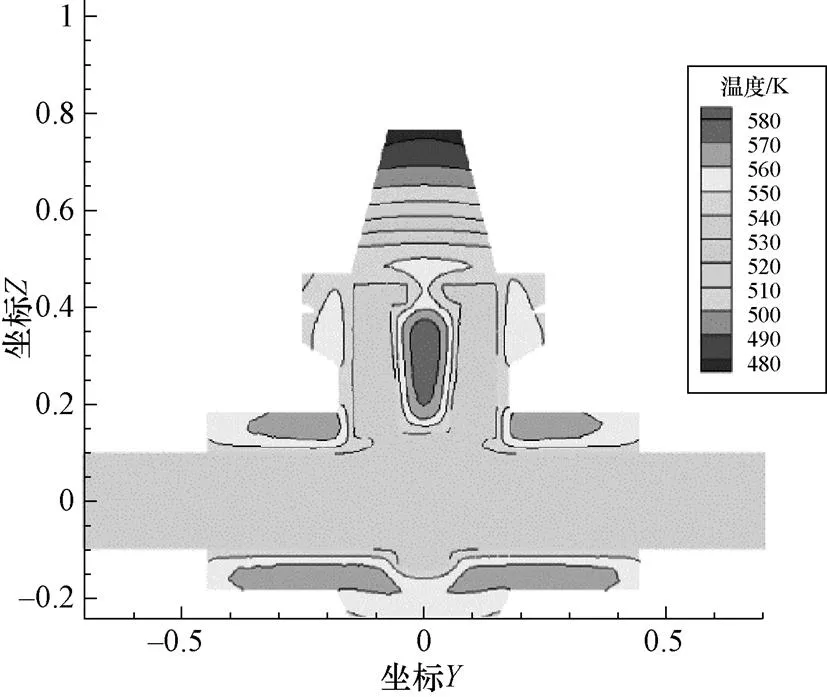
图14　150 s时闸阀内的温度分布

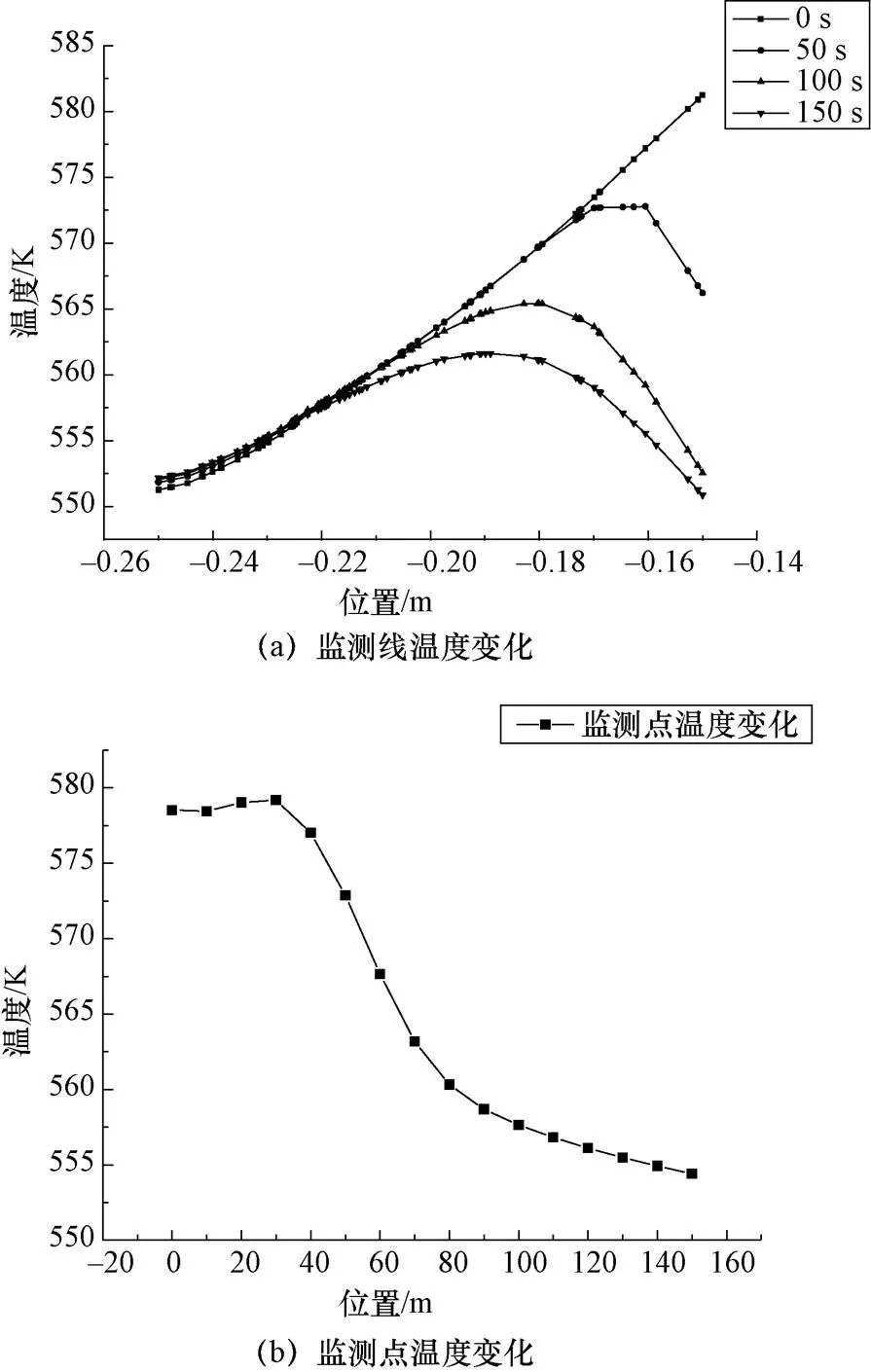
图15　监测线和监测点温度变化

图16所示为闸阀的平均温度变化，在自然对流边界条件时闸阀的平均温度在150 s内下降了9.71 K，而绝热边界条件时下降了10.48 K。总的来说，虽然绝热边界条件和自然对流边界条件计算结果的温度分布差异较大，但是在瞬态过程中温度分布的变化规律是相似的，所以形变也是类似的。

图16　闸阀的平均温度变化

图17所示为150 s时阀体的热应力和形变的分布，参考温度选取为318.35 ℃。与绝热边界条件相比较，取自然对流边界条件时闸阀的最大热应力出现在闸阀两端的尖角处，最大热应力达到了826.81 MPa。闸阀的形变分布较为相似，闸阀的中部形变较大，越接近阀盖处形变越大，最大形变达到了0.641 mm。

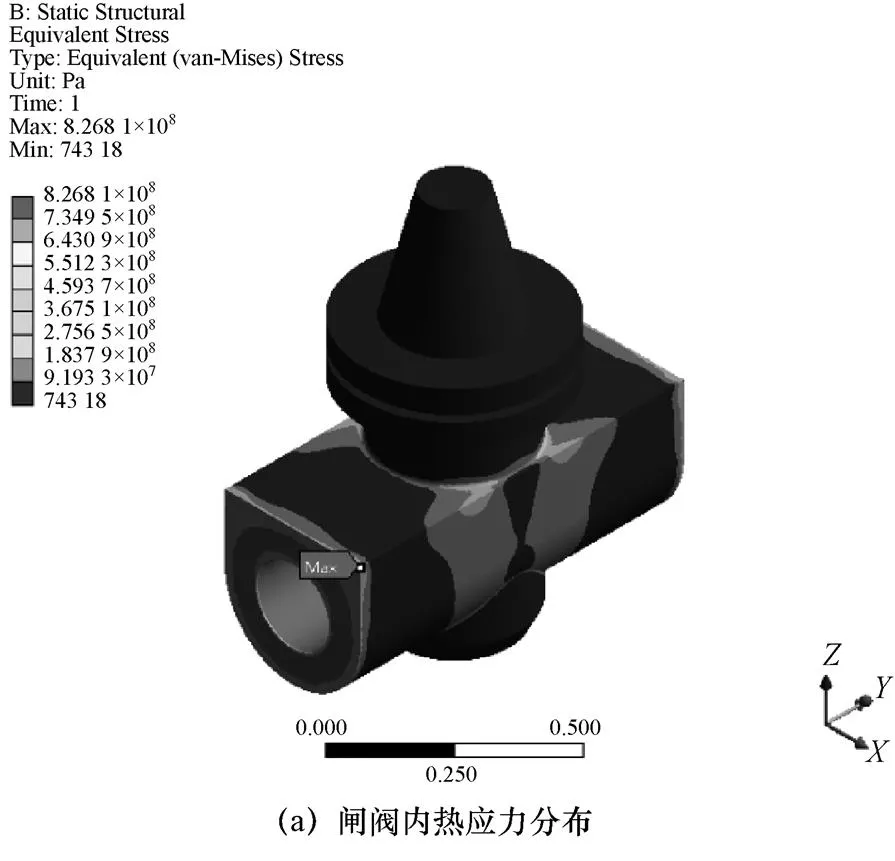
图17　150 s时闸阀内的热应力和形变分布

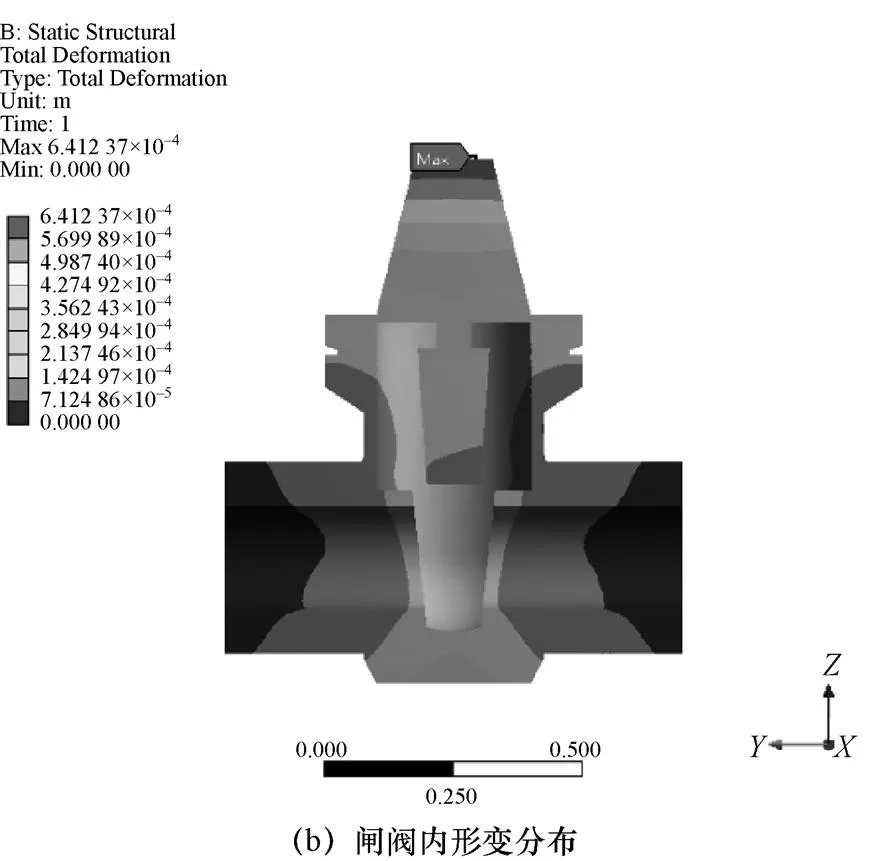
图17　150 s时闸阀内的热应力和形变分布（续）

3　结论

本文对包含部分管路系统的闸阀进行了三维瞬态流固耦合分析，同时对瞬态过程中闸阀的热应力和形变分布进行了分析，得到了瞬态过程中流场、温场、应力场和形变场的详细变化规律。

通过分析，得到如下结论：

（1）标准模型结合尺度化壁面函数可以较好地分析闸阀内的流场和二次流动；

（2）改变流体同阀体的换热可以改变温度变化幅度从而影响形变，所以要想改变阀体的形变量需要从改变流动与换热进行考量；

（3）闸阀自然对流散失的热量相较于流体带走热量非常小。闸阀外表面的热边界条件对瞬态过程中的温度变化规律影响较小，需要注意的是改变换热边界条件后应力极值的位置可能会出现变化。

本工作得到了中国核动力研究设计院国家重点实验室开放基金（HT-JDYYB24-07- 2017001）的支持。

［1］ 秦武，李志鹏，靳卫华，等．核阀的使用现状和发展［J］．通用机械，2008（01）：41-47．

［2］ 熊冬庆，贺振宇，李世欣，等．核电厂主蒸汽隔离阀研制难点分析［J］．核动力工程，2018，39（03）：138-142．

［3］ 王湘江，李必文，蒋果君．谐波传动式核动力装置用闸阀的设计［J］．核科学与工程，2003（04）：375-379．

［4］ 赵英博，张强升，陈天敏．高温锻钢闸阀的温度场计算和热固耦合分析［J］．发电技术，2019，40（02）：181-186．

［5］ Stalio E，Piller M．Direct numerical simulation of heat transfer in converging–diverging wavy channels［J］. Journal of heat transfer，2007，129（7）：769-777

Flow and Temperature Fields, and Deformation Analysis of the Gate Valve in the Transient Condition

WANG Bing1，GUO Yun1,*，XIN Sufang2，REN Chunming2，PENG Qian2，BI Shumao2

（1.University of Science and Technology of China，School of Nuclear Science and Technology，Hefei of Anhui Prov. 230000，China；2. Nuclear Power Institute of China，Chengdu of Sichuan Prov. 610041，China）

The gate valve is an important part of the reactor primary loop. The variation of fluid temperature during the transient process will cause rapid changes in the temperature filed of the gate valve and affect the sealing of the gate valve. In this paper, the computational fluid dynamic method and fluid-structure coupling method are used to analyze the flow field and temperature field of the gate valve including the primary pipe system during the transient process. Through numerical simulation, the evolution laws of temperature in the gate valve during the transient process as well as the thermal deformation and thermal stress are obtained in details. The results can be referenced in the safety analysis of the gate valve.

Gate valve; Thermal stress; Computational fluid dynamics

TL48

A

0258-0918（2022）02-0381-09

2021-01-20

中国核动力研究设计院国家重点实验室开放基金项目（HT-JDYYB24-07-2017001）

王 冰(1996—)，男，河南人，硕士研究生，硕士，现从事核反应堆热工方面研究

郭 赟，E-mail：guoyun79@ustc.edu.cn