基于概率模型检测器的核电厂分布式控制系统动态可靠性分析

夏林路，张雪松，赵鹏飞，陈浠毓，周世梁

基于概率模型检测器的核电厂分布式控制系统动态可靠性分析

夏林路1, 2，张雪松1, 2，赵鹏飞1，陈浠毓3，周世梁1, 2, *

（1.华北电力大学核科学与工程学院，北京 102206；2.非能动核能安全技术北京市重点实验室，北京 102206；3. 中国核电工程有限公司，北京 100840）

分布式控制系统（DCS）是核电厂的神经中枢，对其进行可靠性分析，识别薄弱环节，开展有针对性的设计优化和运维改进，提高电厂安全水平。DCS部件存在备用自投、在线修复等动态行为，传统故障树不能充分描述上述动态行为。针对上述问题，采用马尔科夫模型建立完整的DCS子系统可靠性模型，包括操作终端、PU处理单元、交换机，以及处理器、电源等各类模件，采用概率模型检测器PRISM对马尔科夫模型进行定量计算，得到系统的不可用率，并对系统各失效状态维修率进行了敏感性分析，结果表明，操作与监视系统（OM690）、电厂总线和采集卡失效对系统不可用率的贡献高达95%，因此，通过增加OM690系统、总线设备、采集卡的备件数量和维护人力，可有效提高上述设备的可靠性。

DCS；马尔科夫模型；概率模型检测器；转移矩阵；动态可靠性

DCS是核电厂的神经中枢，多个设备同时故障可导致其控制/保护功能丧失，进而使核电厂关键设备丧失手动/自动控制功能[1]，造成非计划停堆、设备损坏等严重后果。因此，DCS的可靠性分析是核电厂概率安全评价的关键工作之一。

传统的故障树分析方法是以布尔代数为基础的静态逻辑分析方法，处理与时序有关的问题或主设备失效-备用自投、修复等动态行为，一般需对其进行近似处理，使计算结果偏于保守。针对故障树方法的上述局限性，国内外学者开展了大量相关研究工作，文献［1］采用动态故障树法分析核反应堆稳压器数字压力控制装置可靠性，文献［2，3］采用动态流图法（DFM）建立了反应堆功率自动控制系统的动态可靠性模型，文献［4，5］采用BDMP分别建立了核电厂蒸汽发生器水位控制系统和稳压器水位控制系统的动态可靠性模型。这些方法具有各自独特优势，反映了控制系统动态可靠性方法的发展方向。但因建模过程复杂，缺乏成熟软件支持，在控制工程界还没有得到广泛应用。马尔科夫模型是国际国内工控系统可靠性相关标准推荐的控制系统可靠性评价模型，文献［6］已成功将马尔科夫模型应用于DCS的N取K（KooN）表决系统的可靠性分析，文献［7］采用了马尔科夫模型对数字化安全级DCS紧急停堆系统进行了共因失效分析。但尚未见采用马尔科夫模型分析整个DCS子系统可靠性的论文。因此建立了DCS完整子系统的马尔科夫模型，并采用在可靠性界得到认可并广泛应用的概率模型检测器RPISM进行定量分析，根据分析结果，识别了对系统可靠性贡献最大的关键设备，并进行了部件修复率对系统不可用率的敏感性分析。最后，基于分析结果，给出了维护建议。

1　系统的结构和硬件配置

西门子公司的TXP平台由AS620自动化系统、OM690操作与监视系统、ES680工程系统、DS670诊断系统和SINETH1通讯系统组成[8]。核电厂正常运行仪控系统多功能测试、诊断和培训平台由AS620自动控制系统与OM690操作监视系统两部分组成。AS620系统完成工业过程的自动化任务。AS620从过程获取测量的数值和状态，进行开环和闭环控制功能，传递产生的操作变量数值，校正数值及其对过程的命令。其他子系统利用AS620子系统作为过程的接口。AS620传递来自OM690操作员通讯和显示系统的命令至过程，从过程读出OM690、ES680或DS670系统所需要的信息，并传递这个信息到OM690。OM690系统则由SUN、HP等各类型的工业计算机组成[8-10]。其硬件配置如表1所示，结构图如图1所示。

表1　分布式控制系统TXP系统硬件配置表

图1　分布式控制系统TXP架构与连线图

2　系统故障分析

核电厂正常运行DCS多功能测试、诊断和培训平台由AS620自动控制系统与OM690操作监视系统两部分组成。历史上，由于通信中交换机的失效导致的系统故障案例不在少数，且西门子官方也给出了与本系统相关的交换机的失效数据，为了便于分析总线交换机对系统的影响，根据图1核电厂正常运行仪控系统多功能测试、诊断和培训平台架构与连线图，划分出Plant Bus部分，该部分由OSM ITP53和DES-1008D两台交换机构成。

（1） AS620自动控制系统

TXP控制机柜是AS620自动控制系统的主要组成部分，机柜内配置了一对冗余的AP处理器，通过CP1430模件连接到电厂总线，两个AP之间通过IM304/IM324模件实现AP之间的冗余，此机架占两个完全独立的底板总线，它在机架中各FUM模块之间提供连接。在AP中的一个IM 304接口模块和在EU901机架中的一个IM614接口模块提供在AP与一根总线之间的连接。每个EU902机架可以安装19个功能块和2个IM614接口模件。每个总线接口通过一个单独的机架总线与一个单独的IM614接口模块连接。带有功能块的EU902机架通过IM314和IM614接口模块连接到AP。一个IM614接口模块连接到AP（A），另一个IM614接口模块连接到AP（B），从而形成了从AP到功能块的连续冗余总线。

AS620系统中存在AP到功能块的连续冗余，因此当两列均失效的时候，AS620系统就失效了，A列线路由3个IM614和一个IM304模块构成，当其中任意一个模件故障的时候，A列线路就失效了；B列线路同样由3个IM614和一个IM304模块构成，当其中任意一个模件故障时，B列线路就失效了，同时，A、B列线路各模件对应位置、组成、型号均相同，所以需要考虑A、B列线路的共因失效；AP-A处理器模件是主处理器，由AP电源模件、CPU948R模件和CP1430模件，当其中任意一个模件故障时，AP-A处理器模件就失效了；AP-B处理器模件是冗余的处理器，由AP电源模件、CPU948R模件和CP1430模件，当其中任意一个模件故障时，AP-B处理器模件就失效了，同样AP-A、AP-B处理器的模件组成、对应于机架上的位置、模件型号等均相同，也需要考虑共因失效；两个AP之间通过IM304、IM324模件实现AP之间的冗余。当A列线路失效时，若B列线路或AP-B处理器失效时，则AS620失效。AP-A处理器失效时，若B线路或AP-B处理器模件失效时，AS620系统失效。此外，设置了冗余的AP和A、B列线路均存在共因失效（共因失效采用β模型建立在系统马尔科夫模型中），一旦发生共因失效，AS620系统失效。

（2）电厂总线

电厂总线连接了AS620自动控制系统和OM690操作监视系统两个部分，实现了两部分的信息传递，没有设置冗余。本多功能平台中，当OSM ITP53交换机或DES-1008D交换机失效时，认为信息将无法传输，那么电厂总线就失效了。

（3） OM690操作监视系统

OM690系统主要用于对生产过程进行控制核监视，是操纵员与电厂之间的人机接口。在TXP系统多功能平台中主要包括操作终端OT、处理单元PU及AT-FS716交换机。当OT、PU和交换机AT-FS716失效时，OM690就失效了。根据上述的分析，以及实际系统可能出现的故障形态，我们把系统状态分为正常状态、降级失效状态和系统失效状态。其中系统失效状态包括总电源失效、总线失效、采集卡失效、OM690系统失效、切换失效、AP失效、AB线路失效和A/B-AP失效八个状态。降级失效状态包括A列线路失效、B列线路失效、AP_A失效、AP_B失效和切换模件失效五个状态。这个分类为后面马尔科夫模型的搭建提供了状态的参考。

3　失效数据收集与估算

系统各模件失效率主要是通过西门子官方数据确定下来的，而修复率主要是参考某核电站的标准，即模件修复时间不能超过4 h。其失效数据如表2所示。

表2　失效数据表

注：1* 参考研华工控机；2* 西门子官方数据；

根据表3即β因数估计表[4]进行β因子值进行定性估计，TXP系统多功能平台中主要有冗余的AP处理器和冗余的A、B线路存在共因失效，由β=0开始计算，其中冗余的AP处理器安装在同一个机架上，β增加0.01，各自使用独立的电源，有电流地隔离，β增加0.002，它们之间设置了物理隔离，在设计上是相同的，β增加0.01，β因子的估计值为0.022，记为β1。A列与B列线路各个对应传输卡件都安装在同一个机架上的同一块背板上，β增加0.01，使用公共电源，β增加0.01，它们之间设置了物理隔离，在设计上是相同的，β增加0.01，故β因子的估计值为0.04，记为β2。

表3　β因数估计表

续表

4　马尔科夫模型定量分析

马尔科夫模型，是由俄国科学家安德烈马尔科夫提出来的，是一种采用状态图的可靠性和安全性建模的方法。被广泛应用于工业系统的可靠性的分析中[11, 12]。概率模型检测工具PRISM是由M.Kwiatkowska在英国牛津大学开发的。主要用于系统可靠性方面的建模和分析，其可以用于分析离散时间马尔科夫链、连续时间马尔科夫链、马尔科夫决策过程以及概率和时间自动计算模型[13-15]，PRISM通过模块化建模，提高了建模效率，大幅度降低可靠性工程师建模工作量。

4.1　建模假设

（1）只考虑运行失效，不考虑启动失效等。

（2）只考虑硬件失效，不考虑软件失效、操作员误操作失效等其他失效。软件失效和操作员误操作分析方法与马尔科夫方法属于不同体系，在马尔科夫模型中很难准确描述。

（3）不考虑DCS系统机柜背板的失效，公开发表的文献上没有一例背板失效导致的系统失效的案例。

（4）考虑到组合失效的概率极低，为了简化分析，对AS620系统中的AP到功能块的连续冗余部分，只考虑AP-A处理器、AP-B处理器、A列线路和B列线路的两两失效组合，而忽略三个及以上的同时失效所导致的系统失效。这种忽略发生概率极低的组合事件的“截断”方法在概率安全分析中是广泛使用的。

（5）不考虑鼠标、键盘、显示器和ASCLL终端的失效，其失效一般不会导致整个系统失效，修复一般很快（典型值为数分钟到数十分钟），且其产品型号及失效数据难以获取。

（6）不考虑ES680系统，ES680主要用于逻辑功能图的修改、AP代码的生成及传送、MMI画面的修改、生成及传送，是核电厂正常运行仪控系统多功能测试、诊断和培训平台的组态和调试工具。故其失效并不会导致系统失效。

（7）不考虑ESDBA系统管理员站，ESDBA是本系统的调试管理工具，用来对本平台的OT、PU等系统设备进行安装、软件组态灯光工作。其失效并不会使得系统丧失正常运行能力，不会导致系统失效。

（8）系统由各部分失效到正常所需要的修复时间均设为国内某核电站修复时间的标准，即4小时。

（9）不考虑连接网线、电缆等的失效，此类设备若采用满足设计要求的产品并按相关规定铺设，失效率一般很低，将此类失效归并到所连接设备的失效中是广泛接受的做法。

4.2　马尔科夫模型

我们按前面系统状态的划分及故障分析，建立了如图2所示的马尔科夫模型。

4.3　定量分析及结果

使用PRISM验证方法（将马尔科夫模型用PRISM语言描述后，使用PRISM软件输入模型并设置计算参数，包括计算的时间、间隔时间、计算的失效状态等，选择验证方式进行定量分析）。同时通过状态转移矩阵直接进行系统不可用率计算，主要过程是根据系统马尔科夫模型、失效率和修复率，写出状态转移矩阵，对不断进行自乘，直到P+1=P（矩阵中的数值不再变化，达到稳态），得到系统各个状态的可用率，而各个失效状态的不可用率相加便得到了系统的不可用率。系统不可用率随时间的变化情况如图3所示，基于PRISM和直接采用转移矩阵的定量计算结果均为2.198×10-4，系统不能正常工作的概率在万分之一的量级，满足可用率大于99.9%的设计要求，验证了PRISM计算马尔科夫模型的方法的正确性。同时，也得到了不同设备的不可用率及其对总不可用率的贡献，如图4所示，而求得的各设备稳态不可用率分别如表5及图5所示。

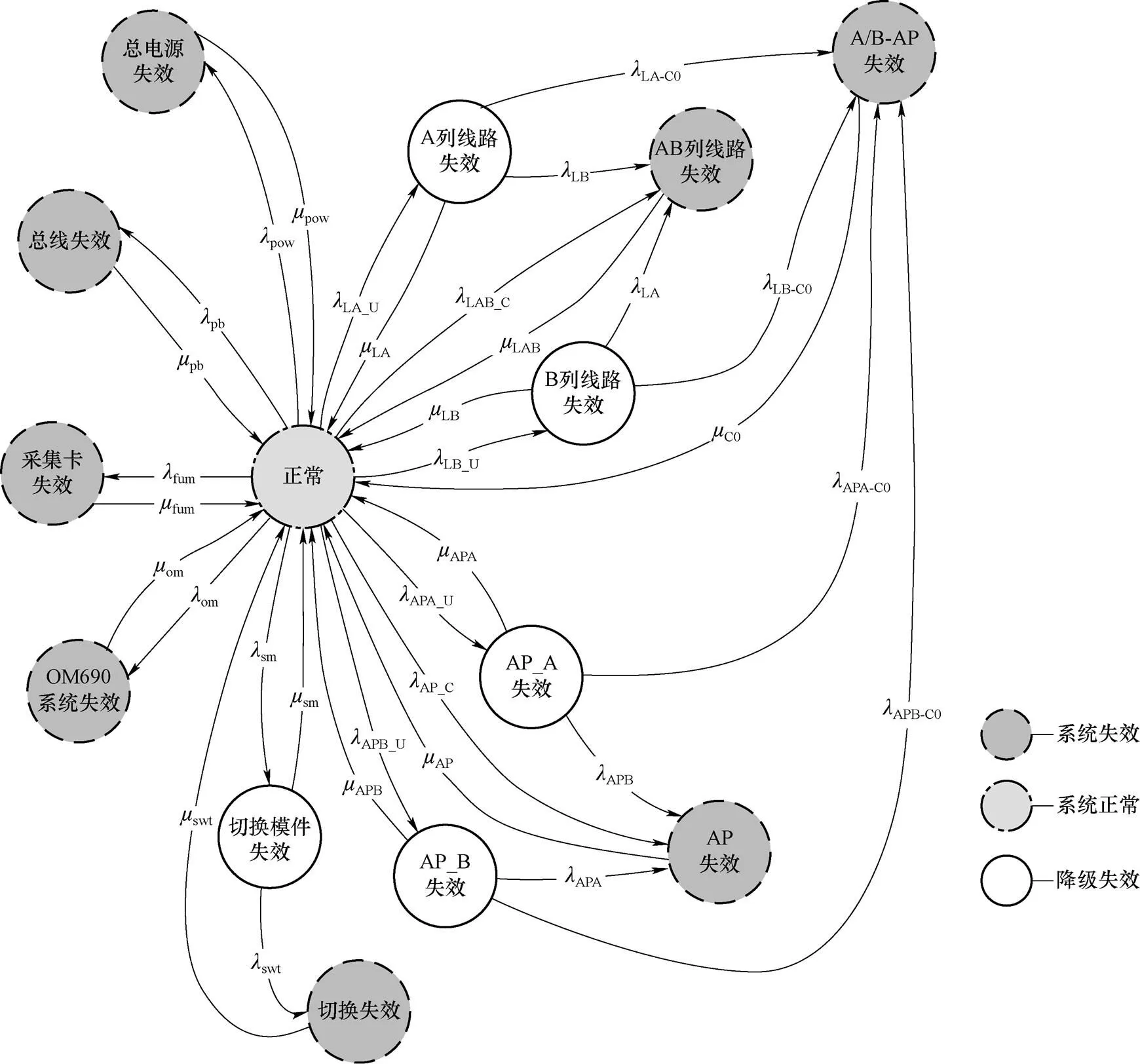
图2　分布式控制系统TXP系统多功能平台马尔科夫模型

图中虚线圈表示系统失效状态，点线圈表示系统正常状态，粗线圈表示降级失效状态，分降级失效状态可以在线修复为正常状态，失效状态可以停机修复为正常状态。图中各参数如表4所示。

表4　马尔科夫模型参数表

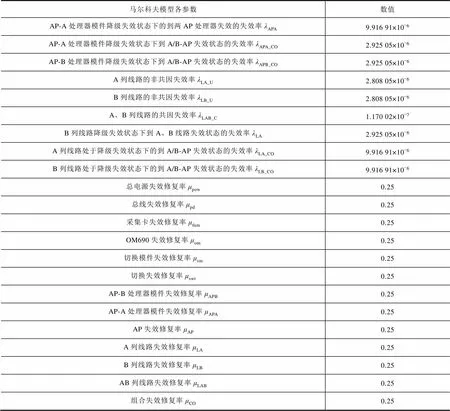
续表

表5　各设备不可用率表

图3　多功能平台不可用率

Fig.3 The non-availability of the multifunctional platform

图4　各系统失效状态的饼状图

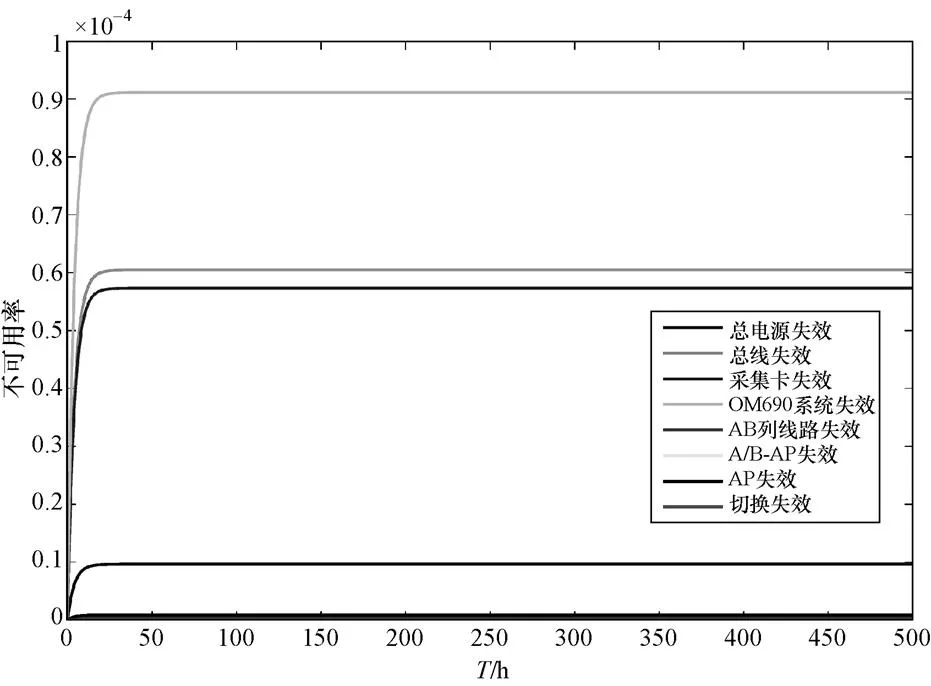
图5　各系统失效状态的失效率

此外，对系统失效状态中的切换失效状态的修复时间取2 h、4 h、8 h、12 h、24 h，而保持其他所有修复率不变，得到不同切换失效修复率swt下的系统不可用率随时间的变化，如图6（a）所示，设（＞1）为维修时间24 h和维修时间2小时系统稳态不可用率的比值，值越大，说明该设备对系统不可用率的影响越大。可知swt约为1，则swt对系统的不可用率几乎没有影响。同理分别对电源失效、总线失效、采集卡失效、OM690系统失效、AP失效、AB线路失效和A/B-AP失效的修复时间按上述方法取2 h、4 h、8 h、12 h、24 h，得到对应修复率下系统不可用率随时间的变化情况，计算出pow、pb、fum、om、LAB、AP、co分别约为1.24、2.74、2.63、4.02、1.02、1.09、1，如图6所示。

5　结论

建立了某核电站DCS完整子系统（包括DCS实时运行涉及的所有子系统和设备）的马尔科夫动态可靠性分析模型，计算了该子系统的不可用率，分析了不同设备失效对总不可用率的贡献，并对各设备的修复率进行了敏感性分析，得到以下结论：

（1）基于PRISM和直接采用转移矩阵的定量计算结果均为2.198×10-4，系统不能正常工作的概率在万分之一的量级，满足可用率大于99.9%的设计要求，验证了PRISM计算马尔科夫模型的方法的正确性

（2）操作与监视系统（OM690）、电厂总线和采集卡失效对系统不可用率的贡献高达95%；

（3） OM690系统、电厂总线、采集卡、总电源修复率降低会显著增加系统不可用率。在运行环境满足设计规定的前提下，这些设备的失效率主要取决于DCS制造商的工艺水平和质量控制能力，维护策略对上述设备失效率影响不大；而适当缩短OM690系统、总线设备、采集卡、总电源的定期检测周期，增加它们的备件数量和维护人力，可有效提高上述设备的修复率，从而显著降低系统不可用率。

［1］ 钱虹，古雅琦，刘鑫杰．基于动态故障树的核反应堆稳压器数字压力控制装置可靠性研究［J］．核动力工程，2019，40（3）：103-108．

［2］ 周世梁，刘玉燕，杜文．基于故障树方法的核电厂数字化反应堆功率控制系统可靠性分析［J］．核科学与工程，2013，33（4）：419-428．

［3］ 周世梁，王浩，田聪．动态流图法对核电厂数字化仪控系统的可靠性评价［J］．核科学与工程，2018，38（1）：88-98．

［4］ 王浩，余嘉炜，周世梁，等．基于 BDMP 的核电厂蒸汽发生器水位控制系统可靠性评价［J］．原子能科学技术，2017，51（12）：2330-2337．

［5］ Mao Yijing，Chen Xiyu，Zhou Shiliang，et al．Reliability analysis of Digital Pressurizer Water Level Control System in NPP based on Boolean logic Driven Markov Process［C］// 2018 14th Probabilistic Safety Assessment & Management conference．International Association for Probabilistic Safety Assessment and Managemen，2018．

［6］ 张庆，马权，许标，等．基于马尔科夫法的核电厂安全级DCS功能安全分析［J］．仪器仪表用户，2016，23（10）：77-81，24．

［7］ 马权，罗琦，宋小明，等．数字化安全级DCS紧急停堆系统共因失效分析［J］．核动力工程，2018，39（3）：95-99．

［8］ 王新，张宝龙，魏龙彪，等．田湾核电站数字化仪控TXP系统多功能平台的研制［J］．中国仪器仪表，2014（1）：55-58．

［9］ 徐正清，王兴叶．西门子TXP系统在扬州二电厂600 MW机组上成功投运［J］．电力自动化设备，1999，19（1）：41-43．

［10］王云伟，冷杉，刘志声，等．虚拟TXP控制系统软件设计与开发［J］．核动力工程，2008，29（6）：128-131．

［11］李元章，何春雄．马尔科夫过程与实用随机模型［M］．广州：华南理工大学出版社，2018．

［12］施仁杰．马尔科夫链基础及其应用［M］．西安：西安电子科技大学出版社，1992．

［13］张国强，殷博，朱静雯，等．基于概率模型检测的移动应用缺陷评估［J］．计算机工程与设计，2019，40（7）：1908-1914．

［14］ Clemens Wiltsche，Marta Kwiatkowska，David Parker. PRISM-games：verification and strategy synthesis for stochastic multi-player games with multiple objectives［J］. International Journal on Software Tools for Technology Transfer：STTT，2018，20（2）：195-210．

［15］ Kwiatkowska M，Norman G，Parker D．PRISM 4.0：Verification of probabilistic real-time system［C］// Computer Aided Verification-International Conference，2011：585-591．

The Dynamic Reliability Analysis of the Distributed Control System of Nuclear Power Plant Based on the Probabilistic Model Detector

XIA Linlu1, 2，ZHANG Xuesong1, 2，ZHAO Pengfei1，CHEN Xiyu3，ZHOU Shiliang1, 2, *

（1. North China Electric Power University School of Nuclear Science And Engineering，Beijing 102206，China；2. Beijing Key Laboratory of Passive Nuclear Safety Technology，Beijing 102206，China；3. China Nuclear Power Engineering Corporation，Beijing 100840，China）

The distributed control system (DCS) is the nerve center of nuclear power plant. It can improve the safety level of power plant by analyzing its reliability, locating its weak links, and carrying out targeted design, operation and maintenance improvement. DCS components have dynamic behaviors such as the standby self-cast and online repair, which cannot be adequately described by traditional fault trees. To solve the above problems, the Markov model is used to establish a complete reliability model of the DCS subsystem, including operating terminals, PU processing units, switches, processors, power supplies and other modules. The probabilistic model detector (PRISM) is used to carry out quantitative calculation on the Markov model to obtain the system unavailability. The sensitivity analysis is also carried out for the maintenance rate of each failure state of the system, the results show that the operation and monitoring system (OM690), the contribution of the failure of power plant bus and acquisition card to the system unavailability is as high as 95%, by increasing OM690 system, bus equipment, acquisition card number of spare parts and maintenance of human, which can effectively improve the reliability of the equipment.

Distributed control system; Markov model; PRSIM; Transition matrix; Dynamic reliability

TL48

A

0258-0918（2022）02-0318-11

2021-01-05

夏林路（1997—），男，湖南邵阳人，硕士研究生，现主要从事DCS系统可靠性方面研究

装备预研重点实验室基金项目资助（6142A07200311）；中央高校基本科研业务费专项资金资助（2019MS022，2019MS036）

周世梁，E-mail：zhoushiliang@ncepu.edu.cn