疫情下考虑疲劳度的可变服务率排队模型

卢宜玲，李军祥，齐缘

（上海理工大学 管理学院，上海 200093）

2020 年2 月11 日，世界卫生组织（WHO）正式将造成肺炎疫情的新型冠状病毒命名为COVID-2019[1]。截至2021 年9 月23 日，全球累计确诊病例达22 937 万人，中国达124 232 人[2]。以中国为例，在疫情爆发达到峰值时，医生的感染占比达到所有确诊患者的2%，并发生多起因医生坚守工作岗位而疲劳猝死的事件。同时，全球多个国家与地区爆发疫情，造成全球性医疗资源短缺。因此，在公共突发的大规模应急医疗中，为了最大程度地提高患者的救治率，实现科学的医生资源分配，协同实施快速有效的救治任务显得尤为重要。

目前，应急医疗资源配置引起了国内外研究者的广泛关注，比如，Belciug等[3]将排队系统、分区模型和基于进化的优化方法整合在同一框架下，对医院科室资源配置进行复杂分析，探讨输入参数的系统性变化对排队系统的结果和资源利用的影响。Cochran等[4]推导出一个开放排队网络模型的急诊科设计，实时地用等待时间和溢出概率作为服务质量目标来衡量区域的大小，旨在提高急诊室的效率。以上研究主要考虑外界因素对整体服务流程效率的影响，探究疲劳度对医生的服务效率产生的影响。现有的医生疲劳度相关研究中，学者们大多采用主观分析法（如问卷调查法和定量打分法）进行研究，但这些方法的科学性和严谨性存在一定的不足之处。比如，殷雪莲等[5]采用疲劳评定量表对急诊医生的疲劳情况进行评分，得出资源的优化及合适的培养模式可能是降低医生疲劳度的有效策略。

疫情期间，医患矛盾更加突出，这也可能是导致医生疲劳度增加的一个重要因素。但实际研究中，很少有学者在研究医生疲劳度的同时，综合考虑系统中排队的患者，大量文献仅限于单独运用排队论、生灭过程、马尔可夫链相关的知识来研究排队系统中各项指标并进行优化。例如，周臻等[6]用排队论模型计算消化科普通门诊患者排队系统中的各项运行指标，并提出合理的配置方案。

本文将急诊科医生作为研究对象，通过分析疫情下影响急诊医生疲劳度的内外疲劳因子，建立可靠的降低急诊医生疲劳度的数学模型，将主观式的疲劳度进行定量化分析，并利用熵权-模糊层次分析法计算各疲劳因子对医生疲劳度的影响权重。其次，运用排队论相关知识将离散稳态的医生服务速率根据医生的工作时间长度分段设置成可变值，建立了多服务台、服务率可变且考虑医生座席轮休制度的患者排队系统生灭模型。最后，建立医生疲劳度与患者排队模型之间的联系，探究急诊医生的最优工作时间段长度。同时，满足医生疲劳度最小化和患者的满意度最大化，实现国家突发公共卫生事件一级响应期间医生和患者之间的双方互利。由于现实系统的复杂性及其本身的随机性，需要使用仿真方法来对系统进行研究。因此，借助ProModel 这一灵活、可靠的离散事件仿真软件，将医院面临的诸多排队问题可视化，从而对其进行有效合理的分析。

1 影响医生疲劳度的内外因子

1.1 问题描述

在系统中考虑复杂多变的内外疲劳因子对医生疲劳度的影响情况，针对不同影响因子制定相应缓解疲劳度的方法。以1 个工作日为单位，研究多名急诊医生1 d 中各疲劳因子的累计值。因医生在工作间隙需休息调整，设ai为第i次工作(i=1,2,···,Φ)，Φ为医生工作次数的最大值。Ti为第i次工作中的工作持续时间。bi为第i次休息，休息时长为。急诊医生的疲劳度与其工作时间成正比例关系，假设当总工作时间超过T时，其服务速率将发生变化，将以一个降低的速率进行服务，从而用生灭过程分析在多服务台可变服务速率的条件下患者的排队情况。系统要求根据患者需求和实时情况制定合理的医生排班计划，降低医生疲劳度的同时最大化患者的满意度。

1.2 疲劳因子

调查研究显示由于疫情的特殊性，医务工作者出于治病救人的心理特征会忽视更多外在的影响因素，但自身无法控制的因素会直接影响医生的疲劳状况。文献[6]根据美国精神行为科学研究室的疲劳评定量表，结合医生职业的情况得到医生的疲劳评定量表排序，选取4 个重要的影响因子进行详细分析。为了准确地体现各项指标对于医生疲劳度的影响程度，采用熵权-模糊层次分析法确定各个指标的相对权重。

1.2.1 内疲劳因子

a.年龄。有研究表明疲劳度与年龄有关，例如：尹绍雅等[7]通过单因素方差及多因素Logistic 回归分析的方法得出结论：年龄大、从业年限长的医生更容易出现疲劳现象。据统计，40 岁以上的医生发生疲劳的概率高达64.3%，明显超过40 岁以下的医生[8]。工作年限高的医生在作业疲劳因子的怠倦感和视觉疲劳感上明显高于工作年限低的医生。

在考虑年龄对疲劳度的影响情况时，假设医生的年龄和从业年限成正比。在应急就诊过程中，精神高度紧张引起的精神疲劳会影响医生的工作效率。40 岁以下的年轻医生单位时间引起的精神疲劳度值为 υ，40 岁以上的年长医生单位时间引起的精神疲劳度值为 υ′，且υ ＜υ′。医生因年龄因素产生的疲劳度累计值设为L1，通过两类年龄段医生人数分别与ai次工作所有工作时段的疲劳值进行求和来表示，即

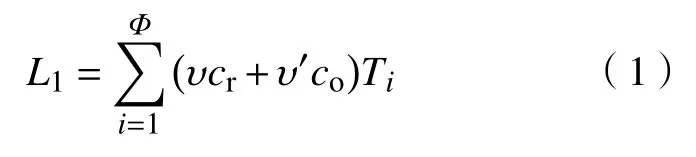
式中：cr为年轻医生人数；co为年长医生人数。

为了综合减少疲劳度，在配置医生比例上要遵从年轻和年长医生人数的均衡搭配，设 Δ1为配置比例系数，以保证两类年龄层级医生在精神层面和经验层面的互补，即

b.性格特征。医生不同的性格特征对疲劳度的感受是不一样的，艾森克用因素分析法提出了神经质、内-外倾性以及精神质三维性格特征的理论[9]。根据内-外倾性理论对医生的性格特征进行分类，假设内倾性格的医生数量为cq，在正常条件下，他们的大脑皮层已具有高度的兴奋水平，其单位时间引起的疲劳度值为 σ，如果进一步提高他们的兴奋水平，那么会增加他们的疲劳效果k1。外倾性格的医生数量为cp，正常条件下，单位时间内他们大脑皮层兴奋水平所引起的疲劳度值 φ相对较低，若提高他们的兴奋水平，相反会减少他们的疲劳效果k2。医生因性格差异所产生的疲劳累计值L2通过两类性格的医生人数分别与ai次工作所有工作时段的疲劳值进行求和来表示，即

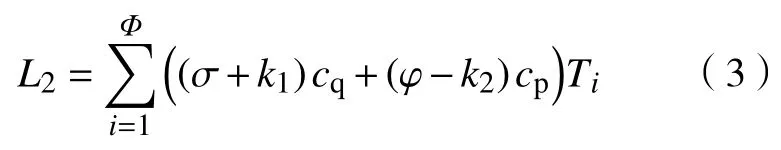
为了减少医生的疲劳度，以避免内倾性格的医生之间进行搭配工作，在实际人员排班中应实行性格互补原则，设 Δ2为配置比例系数，即

1.2.2 外疲劳因子

a.工作压力。医院复杂的环境因素会直接影响医生的疲劳感。急诊科医生在疫情爆发阶段，每天需接待成百上千的疑似患者，首先，暴露在嘈杂的物理环境中而导致人体产生的单位急性疲劳值为m1。其次，医院中仍存在生化有害因子及传染性病毒，导致医生产生的单位生化疲劳值为m2[10]。最后，有研究表明[11]，在遇到众多重症患者时，医生精神高度紧张，心理压力加重，导致其因心理能量耗竭而出现疲劳，医生因此产生的单位心理压力疲劳值为m3。以上工作压力是客观存在并难以轻易消除的。为了缓解医生在紧急环境下的工作压力与疲劳，国家政府单位及医院管理者颁布和制定了对医生的相关激励政策，其所能缓解的单位疲劳效果值设为 ℘。医生因工作压力影响的疲劳度累计值为L3，通过医生数量c在ai次工作所有工作时段产生的3 种单位疲劳值与缓解单位疲劳效果值的累差进行求和来表示，即

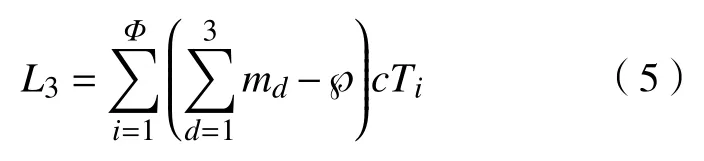
b.休息制度。休息制度的科学性会影响医生疲劳状态。假设以1 个工作日为单位，将医生一天的工作负荷L4作为评估值，用累计工作阶段的疲劳值减去工作间隙休息所减轻的疲劳值，即

式中：c为医生数量；α为医生的工作疲劳度权重系数；γ为医生休息效果的权重系数；A为医生工作期间疲劳度累积值；B为医生休息效果的累积值，即

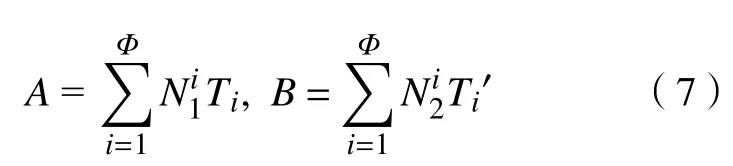
另外，考虑疲劳现象引起恶化效应[12]的现实因素，必须设定一个医生服务时间的上界Timax，避免患者开始时间较晚或排队位置靠后导致实际医生服务时间趋向无穷，即

1.2.3 其他疲劳因子

除了以上分析的4 个内外疲劳因子，医生的工作疲劳状况还与一些可控的因素有关，比如：所处岗位及职称、所承担的责任大小、工资水平、家庭负担及支持度、同事之间的相处模式等[13]。假设将以上的s个疲劳因子作为一个整体考虑，每个因子在每次工作时间段的单位时间内产生的疲劳值为Qϖ(ϖ=1,2,···,s-4)，则各疲劳因子1 个工作日的累计值为L5，通过其他疲劳因子（除上述已分析的4 个以外）与ai次工作所有工作时段的疲劳值进行求和来表示，即

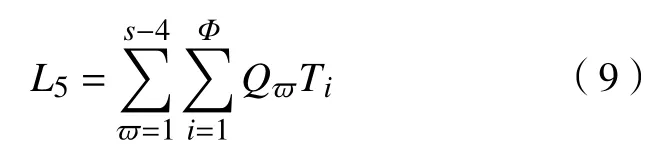
1.3 熵权-模糊层次分析法计算指标权重

在模型研究中，医生的疲劳度是复杂的多因子系统，模糊性较强，采用传统的方法进行描述显得主观性太强。因此，运用层次分析法结合模糊矩阵[14]的相关性质和理论来计算各内外疲劳影响因子的权重（如图1 所示），并用熵对准则层的指标权重进行修正。此方法将主观权重和客观权重结合使用，不仅可以解决不能够准确反映指标的模糊性和不确定性等问题，还可以有效减少主观因素对评价结果的影响，使得评价具有良好的实用效果和可靠性。

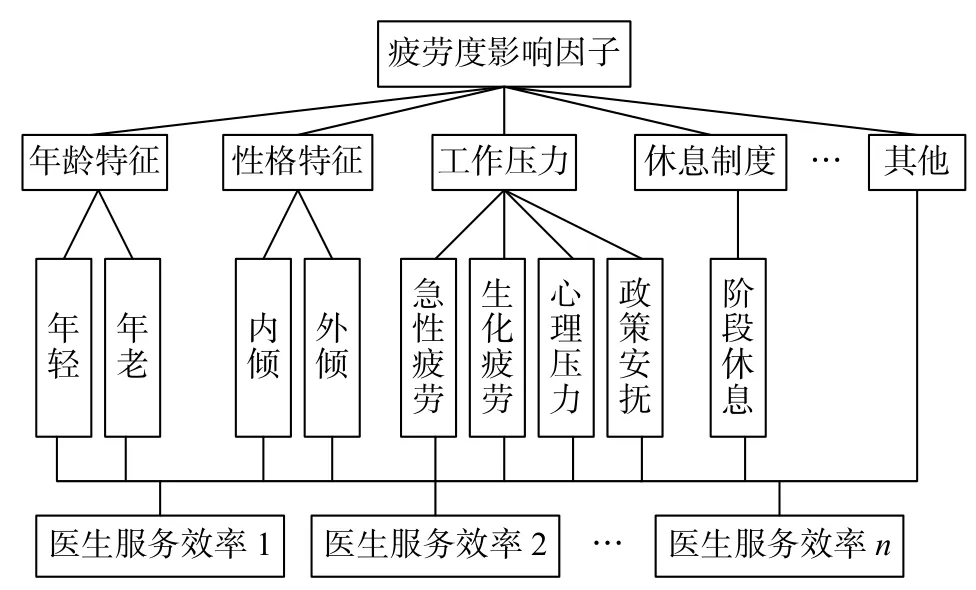
图1 疲劳因子层次结构模型Fig.1 Hierarchical structure model of fatigue factor

1.3.1 构建优先关系矩阵

在构造的层次模型中，因素间的两两比较判断采用对比一个因素比另一个因素的重要程度来定量表示，则得到模糊判断矩阵E=(uvw)x×x，v,w=1,2,···,x分别表示不同的疲劳因子。利用0.1～0.9标度法给予数量标度，如表1 所示，并使用判断矩阵，两两比较各因素的相对重要程度。

表1 模糊标度及含义Tab.1 Fuzzy scale and its meaning

1.3.2 构建模糊一致矩阵

1.3.3 利用公式求出各疲劳因子的权重

因为E=(uvw)x×x是一个模糊互补判断矩阵，W=(e1,e2,···,ex)T是E的权重向量，则W满足

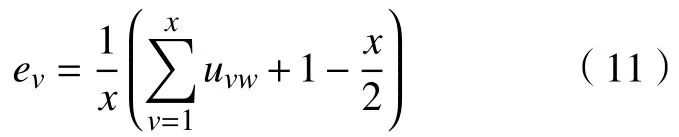
1.3.4 熵权法修正疲劳因子权重

步骤1通过标准化处理后的评价矩阵J=(jvw)x×x计算评价疲劳因子权重的信息熵yv：

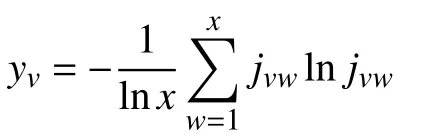
步骤2计算疲劳因子v的偏差指数gv：

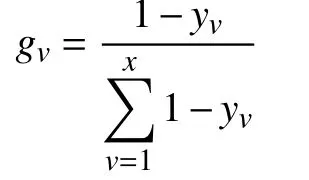
步骤3利用偏差指数对所求权重进行修正：

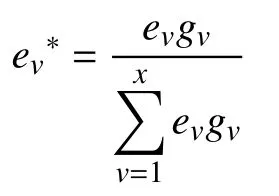
综上，急诊科全体医生1 个工作日中各疲劳因子累计值为

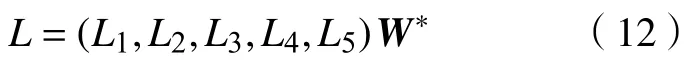
式中，W*=表示修正后的权重向量。

每次工作时间段的平均每时刻疲劳值为

2 考虑疲劳度的可变服务率排队策略

2.1 排队系统规则

排队论是在研究各种排队系统概率规律性的基础上，解决相应排队系统最优设计和最优控制的问题。一般排队系统都有输入过程、服务规则和服务台3 个组成部分[15]。本文结合排队论的相关知识建立针对新型冠状病毒患者的急诊排队模型，将每个急诊医生服务点假设为一个服务台。该模型可描述多服务台排队系统，按照排队论的3 个组成部分进行合理的仿真，如图2 所示。

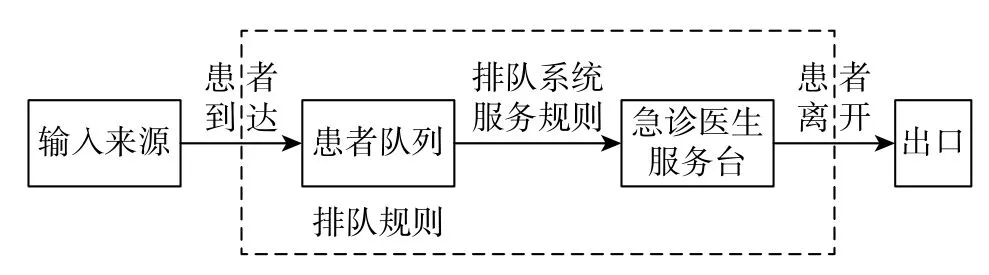
图2 排队流程图Fig.2 Flow chart of queuing

2.1.1 输入来源

输入来源指新型冠病毒疑似患者到达急诊服务台时的规律。对于每一个时段，患者到达急诊服务台的时间间隔可能是随机的，可以近似地假设各类患者的到达时间间隔均服从参数为 λ的负指数分布[16]。

2.1.2 患者排队规则

新型冠状病毒的疑似患者到达急诊服务台后，一般情况应服从先到先服务（first come first serve）的排队规则，以免不公平或插队现象造成不必要的医患纠纷。但是，由于急诊的特殊性，对新冠病毒病症严重的患者实行非强占优先权服务（non-preemptive priorities）[17]，即指当一个重症患者到达时，也需等医生正在服务的患者服务结束后，方可接受服务。

2.1.3 医生服务机构

服务机构指急诊服务台，体现为患者提供服务的数量及规律和每位急诊医生的服务时间及速率。考虑现实情形建立多服务台并联式服务，即给定的c个急诊服务台（每个服务台一位医生进行工作，即服务台数量等同于医生数量）同时为不同患者提供服务，且服务台每次工作时仅服务1 位患者，每位患者不可重复就诊，则设XIΓ为0-1 约束变量，若患者I在服务台 Γ就诊则为1，否则为0，即

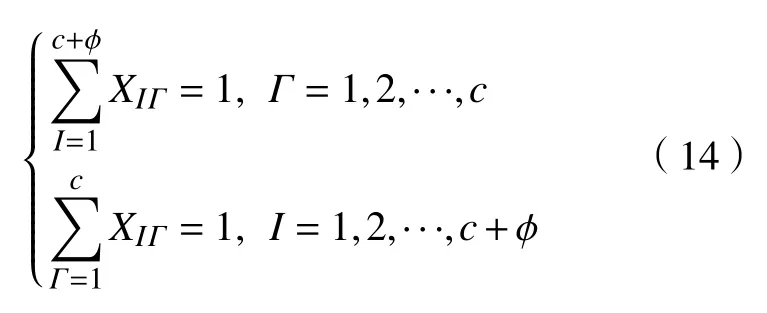
式中，c+ϕ为系统可容纳最大负载量。

2.2 排队系统模型建立

在诊治患者的过程中，可根据当前的医生工作时间改变其平均服务强度。当医生总工作时间未超过T，且此时系统中的患者人数小于c+n时（为了方便后续计算，此时系统总患者阈值用c+n表示），医生的服务速率为 µ1（表示单位时间诊治人数均值），ρ1为患者在快诊治速率下的诊治强度；反之，医生的服务速率 µ2因产生疲劳而有所降低，设 ρ2为患者在慢诊治速率下的诊治强度，其中µ1＞µ2，即

b.因医生需要轮休，假设每次仅一位医生进行休息，则

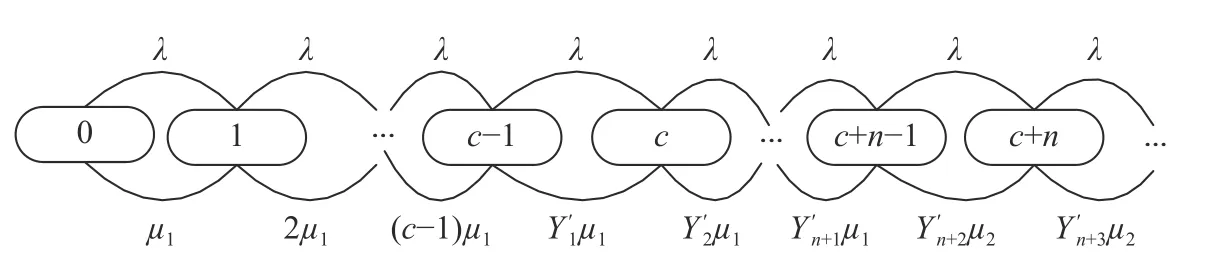
图3 多服务台可变服务速率排队模型流程图Fig.3 Flow chart of variable service rate queuing model for multiple service stations

当系统中患者人数超过服务台人数后开始考虑多服务台轮休制度，其中ι=1,2,···分别表示在系统中状态时医生服务台的服务数量。

对上述情形采用生灭过程进行建模，寻找稳态水平是生灭过程建模的重要问题，现给出生灭过程稳态条件的定理及证明。

定理若ρ1=λ/µ1，ρ2=λ/µ2，且ρi＜1(i=1,2)，即系统是稳定的，则存在服务率可变的排队系统的稳态分布：

证明由生灭过程平衡状态的K 氏代数方程[18]（输入率等于输出率）得：

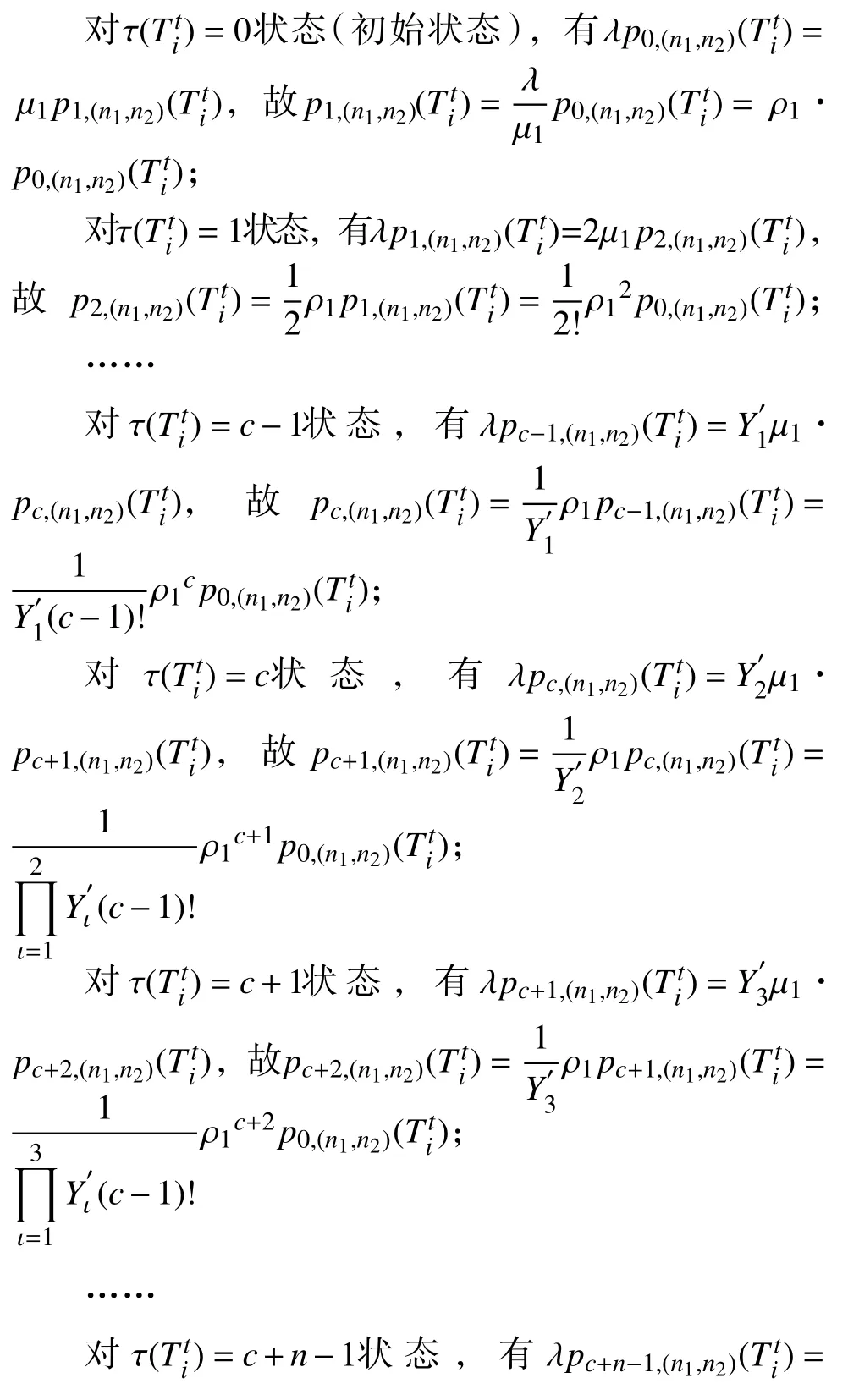
利用以上求得的运行指标，根据Little 公式[19]推出，患者等待时间为

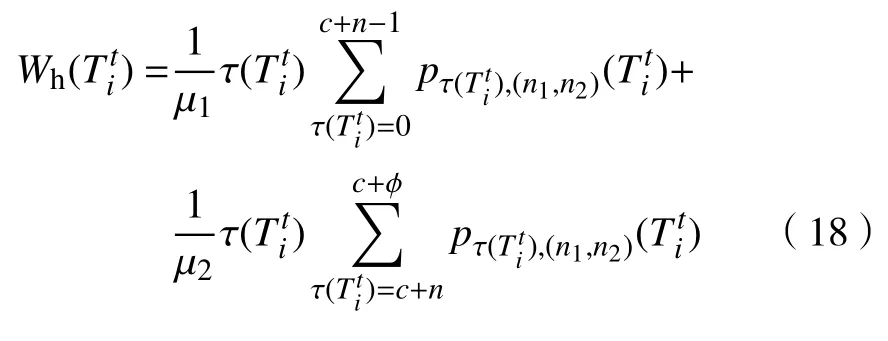
在疫情期间，患者对医生的服务满意度并不是刚性的，此时等待时间则变成决定患者满意度的重要因素。类似文献[20]，假定患者满意度是其等待时间的指数函数：

式中：S为患者的满意度；β(β ≥0)为患者满意度对等待时间的影响系数。由式（19）可知，患者的等待时间越长，则患者的满意度越低。

充分考虑医生和患者双方的需求，以其为出发点，优化目标为急诊医生疲劳度最小化和患者满意度最大化，则

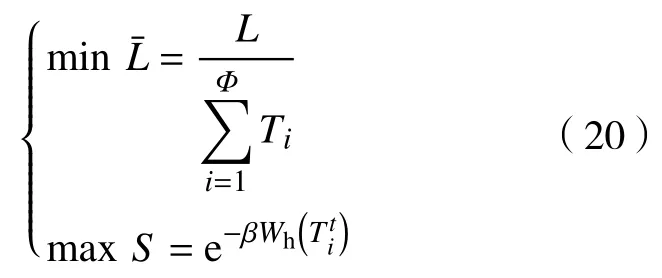
相关文献研究表明[21]，对于多目标问题，一般转换为单目标进行优化。在转换时，因2 个参数指标的单位不同，故对二者进行无量纲处理，使最小，S最大，得到如下多目标联合优化模型：

3 ProModel 仿真

3.1 模型仿真步骤

对考虑疲劳度的可变服务速率排队模型进行仿真优化求解有以下两个难点：其一，由于考虑医生疲劳度的模型具有抽象性、动态性等问题，采用一般的优化算法不易求解；其二，基于生灭排队过程分析有多个运行指标需要经过大量的数据处理，运用现代启发式优化算法反复迭代不仅复杂，且难以考虑其他因素对各运行指标的影响。

借助ProModel 这个模拟离散系统的仿真软件，将整个研究过程可视化，并分类整合各运行数据，其时间分辨率可达0.000 1～36 s[22]，可高效和精确地对模型进行求解。具体运行流程如图4所示。仿真实验根据现实的场景进行，将实验组与对照组进行对比分析，实验组仅增加考虑急诊医生在工作中的内外疲劳因子的影响因素，使服务效率发生变化，其余变量与对照组保持一致，从而判断缓解医生的疲劳度是否对减少患者等待时间和提高满意度有一定的影响。

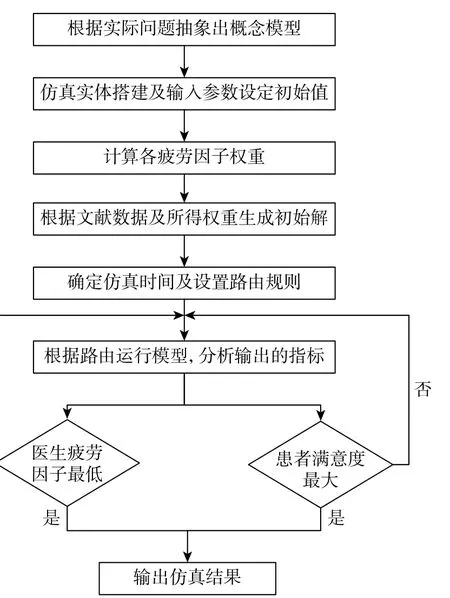
图4 模型仿真步骤流程图Fig.4 Flow chart of model simulation step

3.2 仿真模块分析

3.2.1 Location（位置）

Location 主要用来表示在医院对患者进行排队等待的固定地点或场所、相应的容量及单元数，并设置时间序列（time series）收集基本的数据和追踪位置的时间序列值，定义位置的优先等级及排队规则，如表2 所示。

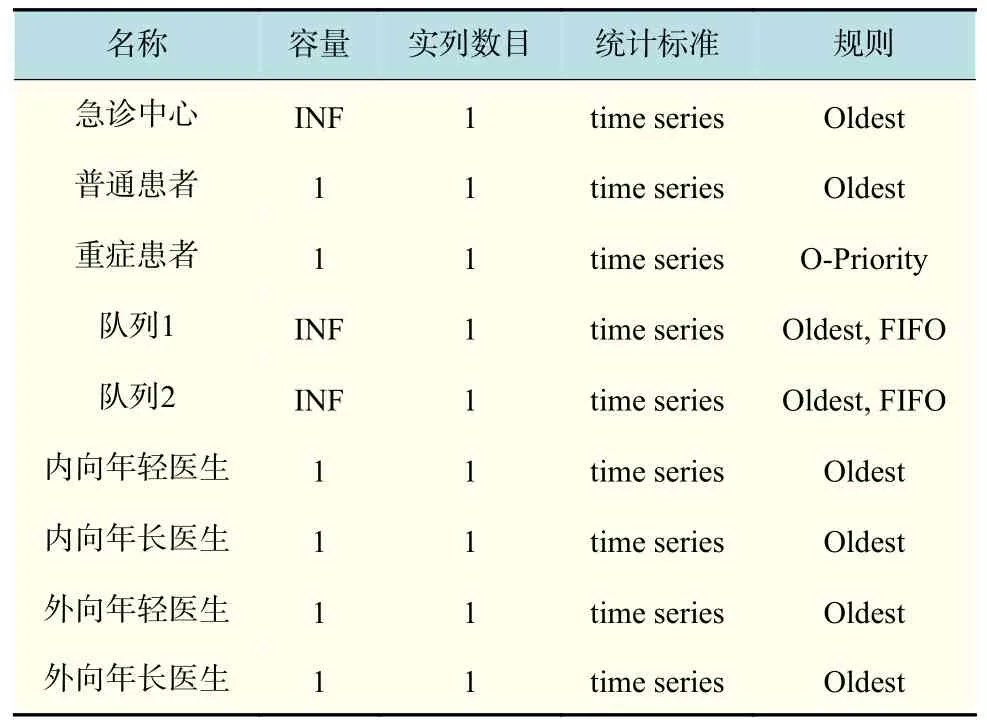
表2 位置界面Tab.2 Location interface

3.2.2 Entities（实体）/Arrivals（到达）

Entities 是仿真要服务的对象，本文指医院中就诊的患者。Arrivals 指新患者进入仿真系统，如表3 所示。表中，P(2)表示患者的到达服从λ=2 的泊松分布。

表3 实体/到达界面Tab.3 Entities/Arrivals interface

3.2.3 Resources（资源）

Resources 是指医生，一般在位置之间移动并且按照路径网络设置的路线运动。仿真配置比例系数 Δ1和 Δ2均为1。资源模块主要包括详细参数设置，如医生分配路径网络、医生速度、服务每个患者的时间。收集统计资源中所有单元的平均利用时间和活动时间。设置每个医生座席停工时间，考虑模型的可实现性，假设各服务台医生每次工作时长近似相等。由于轮休、初始和末尾工作阶段时长之和近似相等，依旧取其均值进行分析，休息、轮班如图5 所示。其中，停工时间设置每个座席停工时间的优先级（包括进入及保持休息的优先等级），目的是为了保证医生在预设的休息时间结束之前回到座席，运用逻辑节点来定义医生进入或者离开某个节点的逻辑动作。

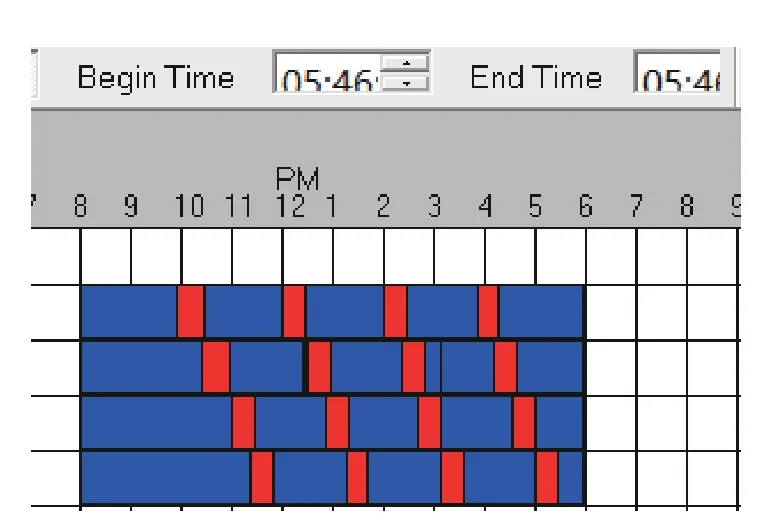
图5 医生座席轮休图Fig.5 Rotation of doctors' seats

3.2.4 Processing（处理）

Processing 定义了患者在仿真运行中的路由，也定义了患者进入每个位置上的作业内容。设置各个患者和医生之间的逻辑关系，通过使用系统函数及数学语句实现医生的疲劳度约束，利用处理编辑表为系统中每个位置的患者创建操作逻辑及移动逻辑来实现模型约束。

3.3 模糊层次分析法计算各疲劳因子权重

赋值v,w=1,2,3,4,5分别表示年龄特征、性格特征、工作压力、休息制度、其他疲劳因子。通过相关文献研究得到各数量标度即疲劳度的相关性系数[13]，得到相关性分析结果，如表4 所示。

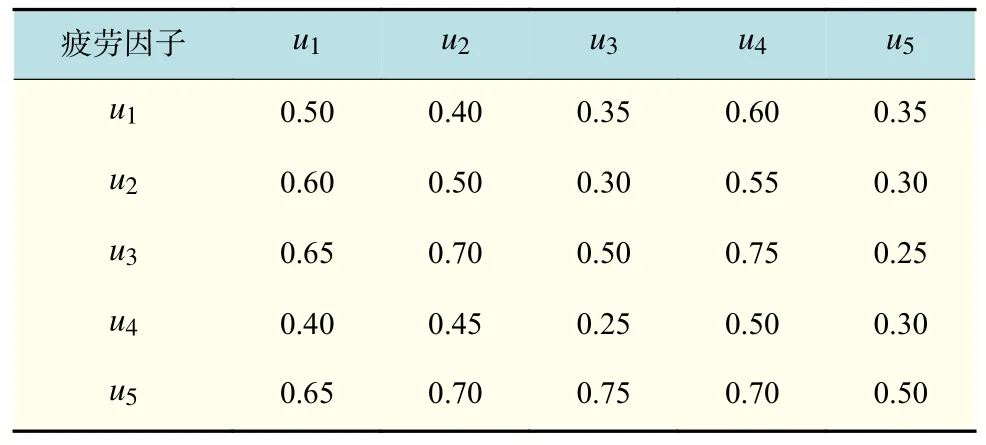
表4 相关性分析结果Tab.4 Results of correlation analysis

在计算内外疲劳因子对医生疲劳度的影响权重过程中，通过式（10）验证唯一靠人的主观而给出的模糊互补判断矩阵已通过一致性检验。根据式（11）及熵权法修正权重步骤1～3 计算得出内外疲劳因子对医生疲劳度的影响权重如表5 所示。

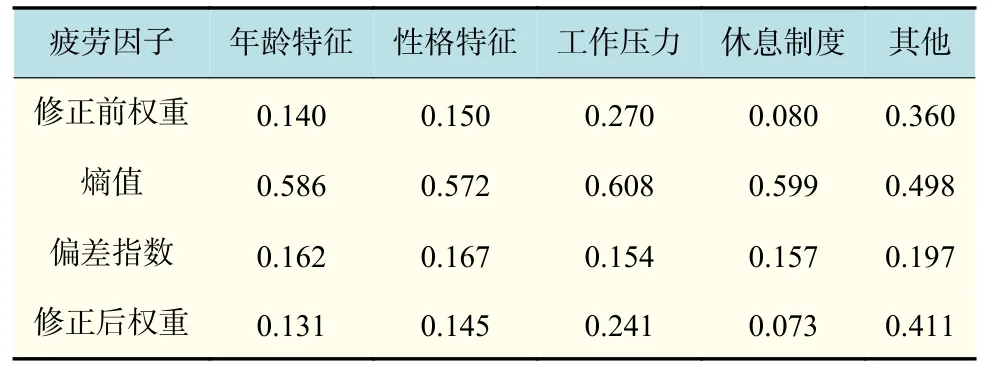
表5 熵权修正后的疲劳因子权重Tab.5 Entropy-weighted corrected fatigue factor weights

在内疲劳因子仿真中分别探析不同年龄和性格医生的各服务指标，从而创建多条路由，其权重用在选择路由目标的规则（Rules）模块中。外疲劳因子各种类医生均受用，因此不分别讨论，其权重用在资源（Resources）模块的路径网络中。熵权-模糊层次分析法所得权重更加细化了仿真的约束条件，增加了仿真结果的精确度。

4 数值分析

优化模型中 ς的取值对P产生影响，不同的 ς可能出现不同的评价结果。由文献[23]中医生和患者的演化博弈模型结论得出：在考虑医生的疲劳度和患者的满意度处于1∶1 均衡时，预期可达到均衡。因此，在仿真实验中将 ς取0.5 的固定系数进行求解分析，对二者赋予同等权重。

根据上述仿真输出结果，可作如下分析：由表6 仿真结果可知，考虑医生疲劳度的医生服务模型中，其实际总工作时间明显降低，控制在8.68 h。与此同时，各项服务指标也发生了变化，传统医生服务模型的队列阻塞率高达57.69%，医生门诊座席的平均空闲率达49.23%。由此，可初步判定，队列如果长期处于拥堵的状态，并且门诊座席的利用率不高，将造成时间成本和人力成本的浪费。由人因工程学相关经验，人员工作空闲率一般控制在15%～25%。在考虑医生疲劳度的医生服务模型中，队列阻塞率下降了22.2%，且座席的平均空闲率降低了22.99%，医生服务率提高了27.54%，总体的利用率达到了优化的效果。

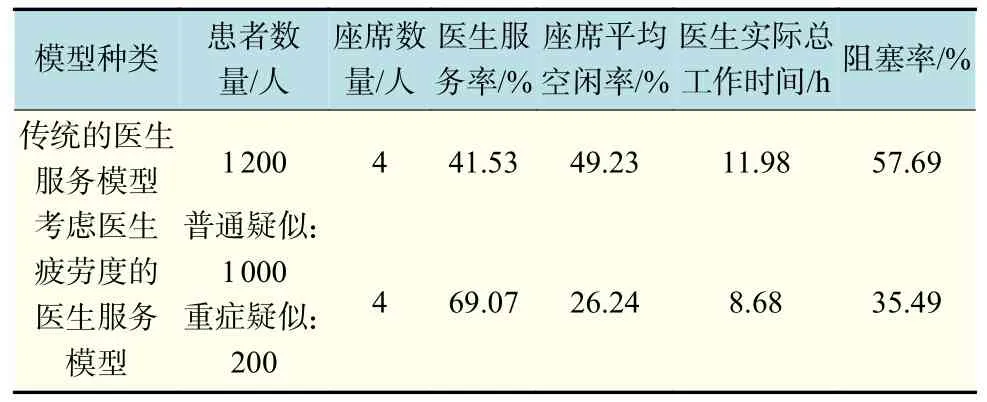
表6 仿真结果Tab.6 Simulation results

如图6 所示，在考虑医生疲劳度的模型中，分别研究不同性格、年龄医生的座席利用率。优化后的各座席利用率明显高于不考虑医生疲劳度的座席利用率。由此可见，若医生产生一定的疲劳度，对其座席的利用率是有一定影响的。其中，外向年长的医生座席利用率一直处于较高的水平，说明该种类的医生临床经验丰富，心理素质较强，在面对高强度工作时能保持最佳的状态。相反，内向年长医生在降低其疲劳度之后，依然有2 个时间段的座席利用率低于优化前，说明在面对高压高强度的紧急事件时，内向年长的医生可能会有更高的心理压力，导致其座席利用率不高。年轻医生的座席利用率的增速明显较快，因经验不足，在适应一段时间后，接受新鲜事物能力较强。因此，在抗疫期间，年轻医生成为了不可或缺的主力军。

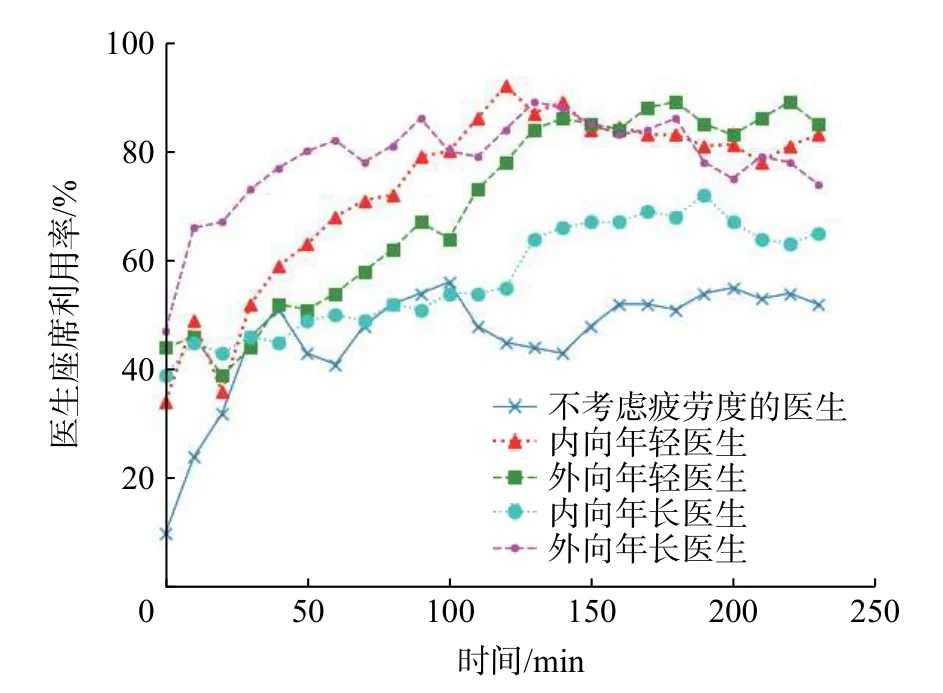
图6 医生座席利用率对比图Fig.6 Comparison chart of doctors' seat utilization

如图7 所示，对模型优化前后各医生座席的服务效率进行对比分析。不考虑医生疲劳度的座席服务效率呈下降的趋势，说明医生的疲劳状况会影响其服务效率。在考虑了医生疲劳因素后，对年轻医生的服务效率有明显的改善作用，说明本文提出的科学轮休制度等相关方法对改善年轻医生的身体和心理具有一定的帮助。而年长医生的服务效率均在一定范围内进行波动，没有明显的下降趋势。因此，医生疲劳度的降低对各医生座席的服务效率均有正向影响。

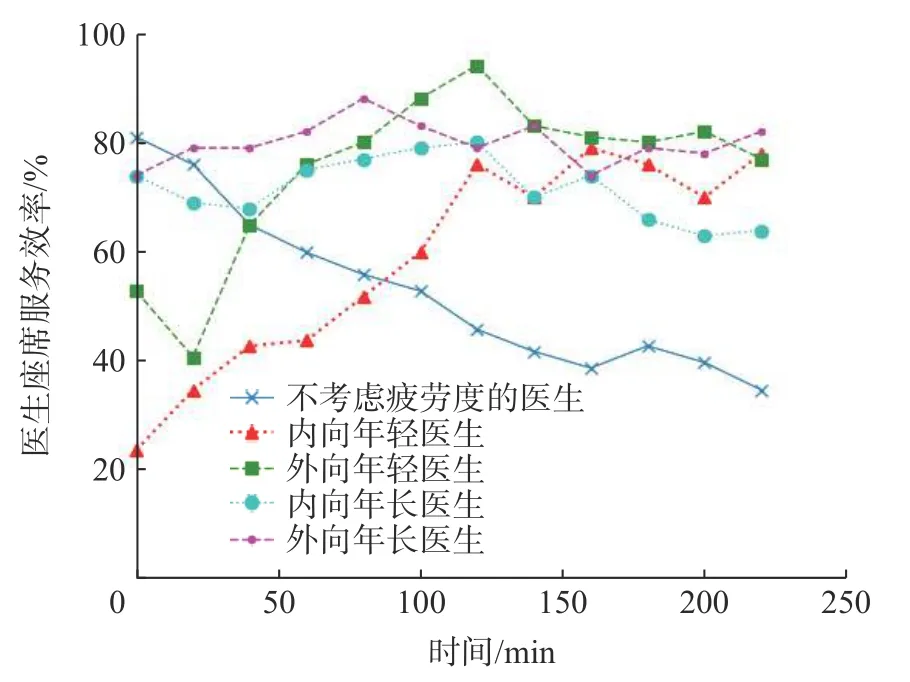
图7 医生服务效率对比图Fig.7 Comparison chart of doctors' service efficiency

如图8 所示，可以得出两点结论：其一，由于重症疑似患者到达队列时，有非强制优先权，因此重症疑似患者的输出率均大于普通疑似患者，从而保证了高效筛选和检查重症患者；其二，在考虑医生疲劳度的模型里，其患者输出率均大于不考虑医生疲劳度模型的患者输出率，换言之，降低医生单位时间内的疲劳度后对患者的输出率有正向影响作用。

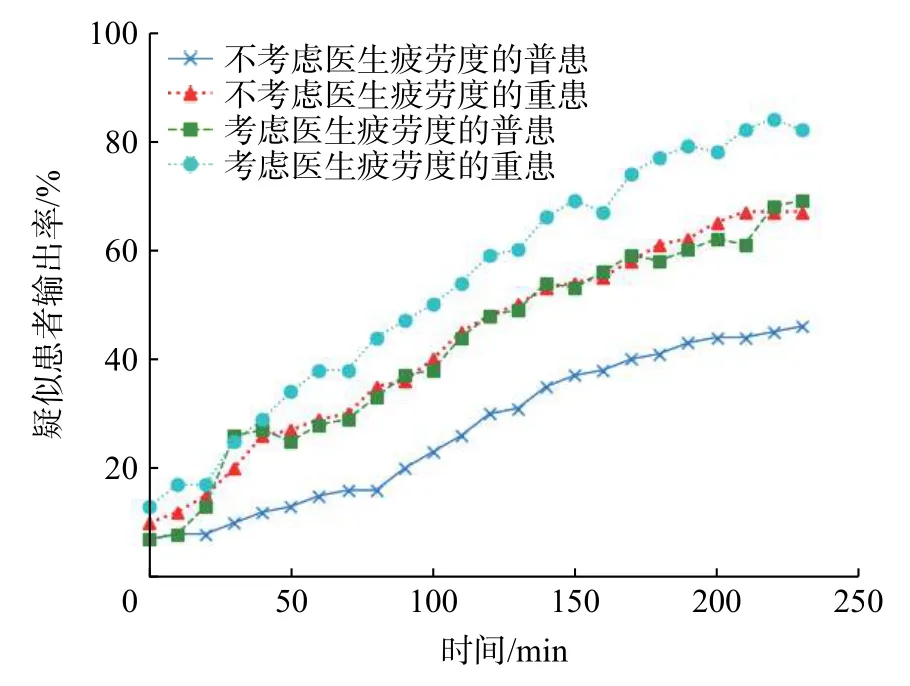
图8 疑似患者输出率对比图Fig.8 Comparison of output rates of suspected patients

图9 描述的是患者等待时间及患者满意度的一个双坐标轴图。无论是在疫情期间还是日常就诊，患者的等待时间是评价患者满意度的一个重要指标。尤其在此次新型冠状病毒疫情期间，感染者人数众多，时间尤为紧急，这严重影响了患者的满意度。考虑医生疲劳度的优化模型，患者的等待时间明显低于传统模型，这说明通过对医生座席的合理调度和患者排队的科学安排，能够有效提高患者的满意度。

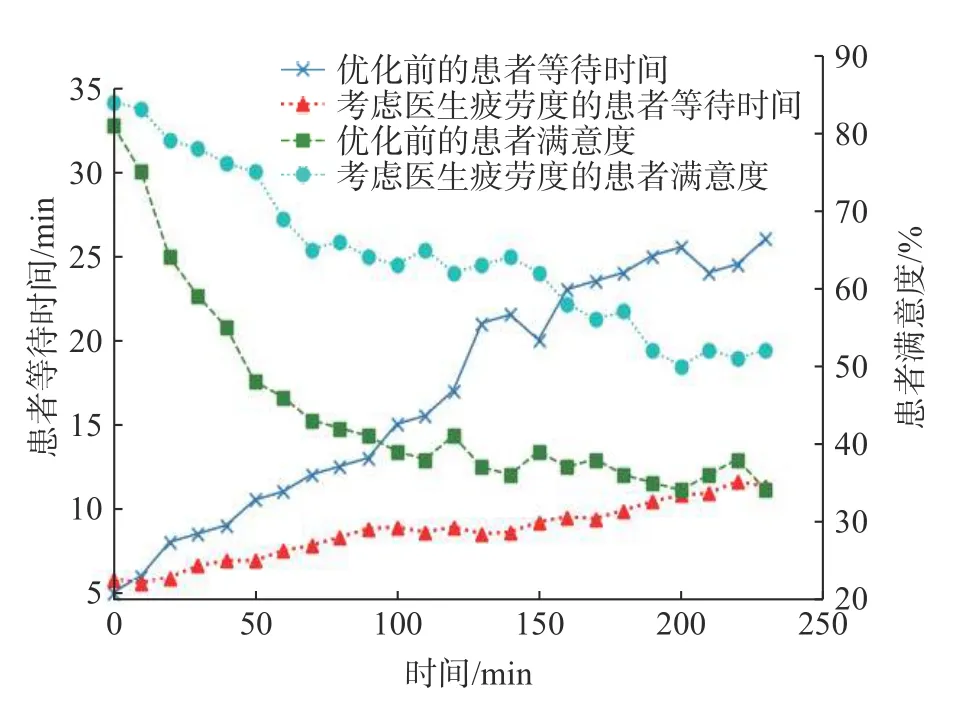
图9 患者等待时间和满意度对比图Fig.9 Comparison of patients' waiting time and satisfaction

5 结论

降低医生的疲劳度不能仅从政策福利的角度来进行，还需要考虑医生自身的基本属性。本文考虑医生内外疲劳度影响因子，分析疫情下如何将医生疲劳度和患者的满意度达到一种动态平衡，优化医患双方利益。内外并进地对医生进行合理搭配排班，科学制定休息时间，加强对医生的政策保障，是缓解医生的疲劳度和提高医疗服务工作的重要因素。其优化结果对紧急突发事件中合理调整医生的日工作量、工作密度、最大负载，以及合理安排休息时间、改善工作条件等提供了科学依据。本文使用ProModel 仿真软件，通过对实例进行仿真分析，说明了仿真方法对于研究问题的有效性。作为对数学建模及求解方法的一个补充，运用理论方法考虑医生疲劳度对服务效率的影响具有局限性，仿真研究可以使优化方法更适合现实场景的应用，具有很强的理论及现实意义。