水平管内积液特性的实验及理论预测模型

马有福，曾珊珊，吕俊复，吴雨昕，张玉燕

（1.上海理工大学 能源与动力工程学院，上海 200093；2.清华大学 机械工程学院，北京 100084）

在天然气开采中为提高气井产量，希望伸入气田目的层的井段与产气层有最大的渗流面积。水平气井在增大气井渗流面积从而大幅提高气井产量方面具有明显优势[1]。积液现象是影响气井稳定生产的主要问题之一。气井中的液体主要来自地层中的间隙水以及烃类气体在上升过程中降温形成的凝析液。若井中气相不能提供足够的能量使液体连续流出井口，井中就会出现积液。积液使气相渗透率减小，从而降低气井产量，严重时可能导致气井停产[2]。因此对水平井内积液特性进行研究具有重要意义。

管内积液现象类似于管内气液两相逆向流动中使管内倒流液量恰好为零的工况，该工况下的管内表观气速常被称为临界携液气速。为预测临界携液气速，目前存在两类模型——液滴模型[3-4]和液膜模型[5-8]。在临界携液工况下，液滴模型认为液相主要以液滴形式被气流带出气井，液膜模型认为液相主要以液膜形式沿着管壁流出气井。针对垂直气井，Turner等[3]分别基于液滴模型和液膜模型提出了临界携液气速预报模型，并基于气井生产数据提出了相应的关联式。近期Zhang等[4]进一步区分了垂直井内出现积液时的3 种流型，针对每种流型提出了相应的最大液滴尺寸预测关联式。潘杰等[9]在液膜模型基础上进一步考虑了液滴夹带对垂直井内实际气速及相界面剪切力的影响，并通过气井生产数据分析了模型的预测准确性。在倾斜气井中，气、液两相倾向于分层流动，因而多是采用基于液膜模型的关联式预测临界携液气速[10]。Chen等[7]在Turner 液膜模型的基础上考虑了气井倾斜对液膜重力的影响，从而得出倾斜井积液预测模型并通过相关实验数据分析了模型的预测性能，但该模型仍是以管内环状流为基础进行分析。

迄今对水平井内积液的研究鲜有报道。在常见的气井管径范围（≤100 mm），积液工况下水平管内气液两相流动呈典型的分层流流型，因此以往基于环状流或搅拌流的分析模型均不适用于水平管内的积液预报。此外，水平管与垂直管的积液特性有明显差别。在垂直管内，积液发生工况（管内液体恰好不倒流）与积液排出工况（管内液体恰好连续排出）之间的气速差别较小，因而以往文献中未对二者进行严格区分。而在水平管内，积液发生与积液排出对应的气速差别非常明显[10]。为深入认识水平管积液机理并建立相应的预测模型，笔者对水平管积液特性进行了气液两相流动实验，并通过一维两相流动分析建立了水平管积液预测模型。

1 实验方法与数据处理方法

1.1 实验方法

1.1.1 实验系统

实验以常温的空气和水作为两相流体，采用管长2 m、矩形管截面尺寸高×宽106×60 mm 的有机玻璃水平管进行积液特性实验，实验系统见图1。环境空气经高压风机升压后，依次经过空气稳压箱（降低气流脉动）、整流格栅（降低气体湍流度）、低位水箱（防止水倒灌入风机）和水平管测试段后进入高位水箱，再由高位水箱顶部排入大气。给水箱内的水由水泵送入高位水箱。在高位水箱的排气口侧面设置了玻璃观察窗，排气口对面正对测试管的管轴设置了溢流管。实验过程中保持水泵运行使水从溢流管连续流出，从而维持高位水箱内水位稳定。如水平管内风速不足以维持管内积液状态，高位水箱内的水会经水平管流入低位水箱。实验中低位水箱底部保留一定水位，从而防止气体从水箱底部排水阀泄露。

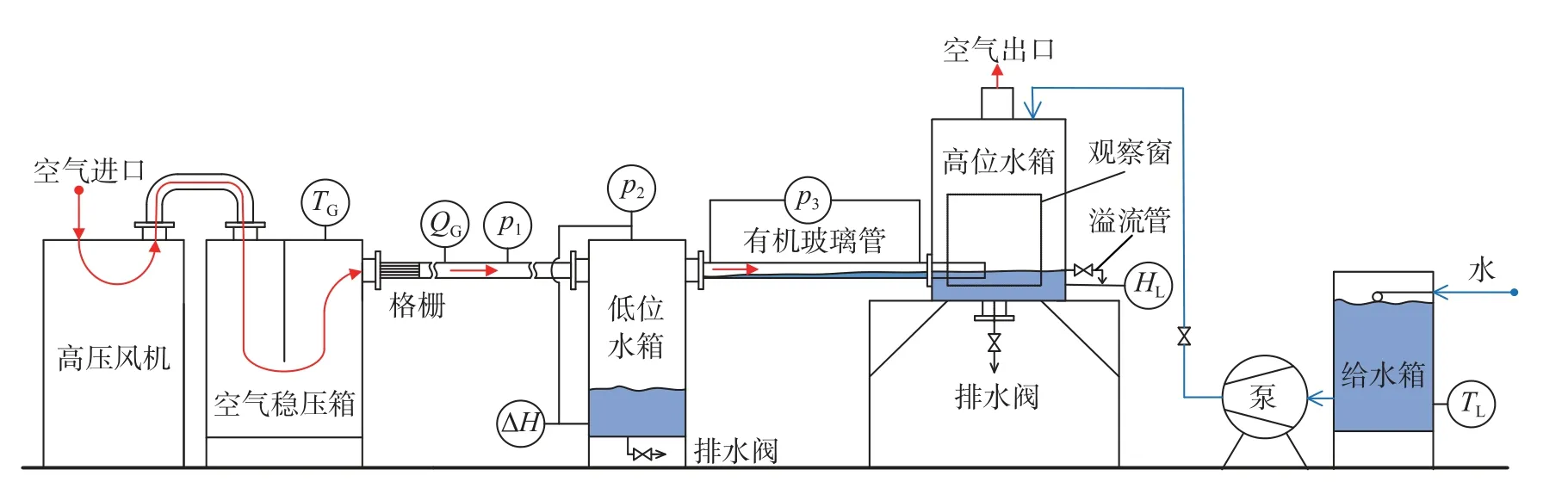
图1 水平管积液特性实验系统Fig.1 Experimental system used for the liquid loading of horizontal pipes

1.1.2 测量参数

本实验通过测量仪表确定空气在水平测试管内的流量和沿程流动压降，同时监测高、低位水箱的水位高度，采用的仪表见表1。水平管内的滞留水长度和滞留水液面倾角由图像法确定。在一个稳定工况下，各仪表输出的模拟信号由模块采集并输入计算机，同时通过相机拍摄管内两相流动图像。

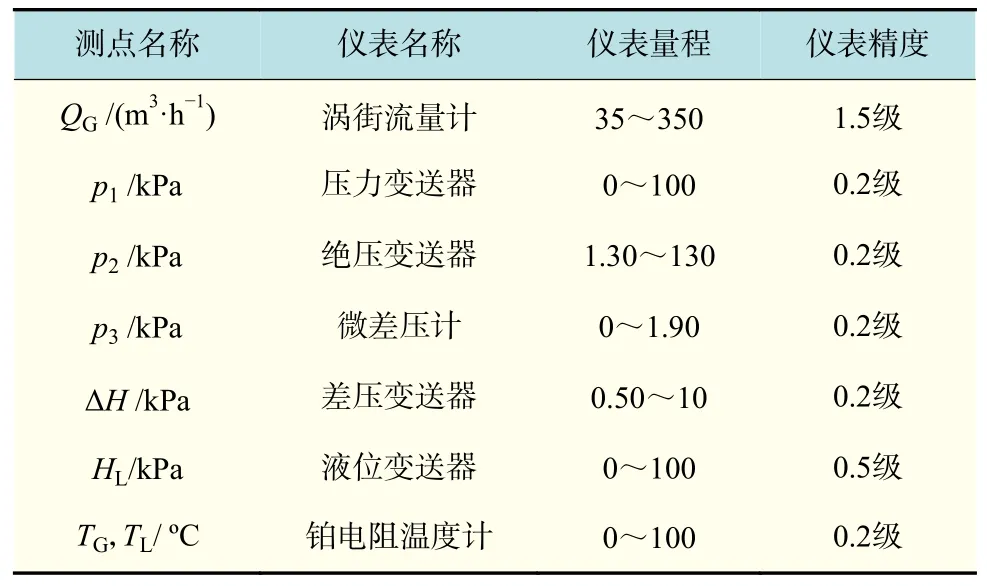
表1 实验用仪表Tab.1 Instruments used for the experiment

在靠近气体流量计和水平管入口的位置设置压力测点，并测量气体温度，从而由气体流量计测得结果换算出水平管内气体容积流量。在水平管上方设置2 个取压孔，由微差压计获得沿管长的气相压降。入口侧取压孔距离水平管进口100 mm，出口侧取压孔距离水平管出口200 mm，取压孔间距1.70 m。

1.1.3 实验过程

首先进行积液特性实验。a.开启高压风机，调节风机风量至较大值。b.开启水泵，向高位水箱注水至高位水箱溢流管有水流出；调节风机风量，使水平管内无积液。c.通过变频调节逐渐减小风机风量，至水平管内有水滞留；在一个稳定的管内滞留液长度LW（排气口至管内滞留水末端的水平距离）下采集实验数据；LW随风机风量减小而增大，在LW为 0～2.0 m 范围内采集6 个稳定工况；同时通过拍摄每个实验工况下水平管内的积液照片，获得管内滞留液长与液面倾角。

之后对该矩形截面水平空管进行气相压降实验，以获得该水平管的壁面剪切因子。该实验中气相流量范围参照积液特性实验的气相流量范围确定，在该流量范围内测量了6 个工况。

1.2 实验数据处理方法

1.2.1 气相Wallis数

在管内气液两相逆流极限（cunter current flow limitation，CCFL）研究中，常通过无量纲气相Wallis数[11]表征管内气速大小。管内积液与CCFL流动中的零液渗透点（Zero Liquid Penetration）相似，故本文由气相Wallis 数表征管内气速，其表达式为

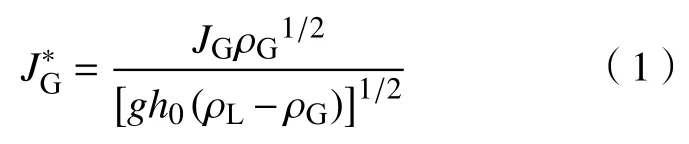
管内气相表观流速JG为

式中：QG为管内气相容积流量；A0为水平管的流通横截面积。

1.2.2 滞留液长

在水平管内，积液现象在一个较大的JG范围内始终存在[16]，在该范围内，管内积液的滞留长度LW随JG的增大而减小，如图2。因而本文通过关系表征水平管积液特性。LW的确定方法为：将积液照片导入AutoCAD 软件中，以已知水平管长度2 m 为标尺，按比例求出LW。对于水平井，LW的大小可表征积液的范围大小或严重程度，因而由表征水平管积液具有明确的物理意义。

图2 水平管内积液实况图Fig.2 Flow scenes of liquid loading in the horizontal pipe

1.2.3 液面倾角

为通过实验获得气液两相界面剪切因子，需确定积液工况下的管内空泡份额。在水平管内，积液的液层厚度沿气相流动方向逐渐增厚，即：管内滞留水的液面呈一定倾斜角度，在积液段，管内空泡份额沿气相流动方向逐渐减小。为求得积液段平均液膜厚度（即平均空泡份额），本文由图像法确定LW的同时，也用相同方法获得液面倾角θ，如图3。

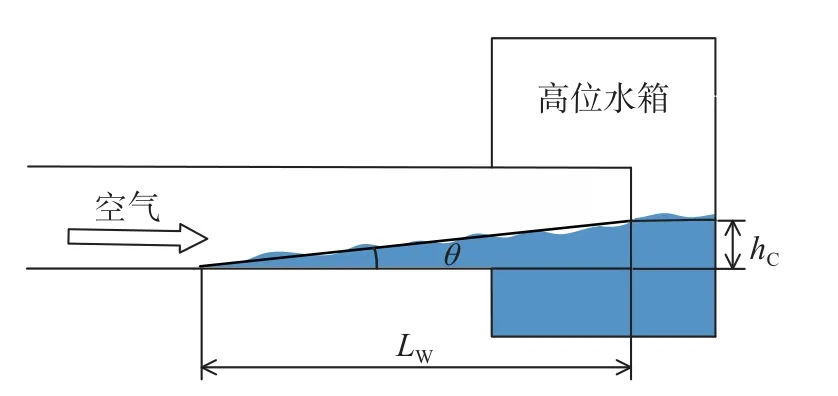
图3 水平管内积液的滞留液长与液面倾角Fig.3 Liquid length and inclination angle of the liquid loading in horizontal pipes

进而求出水平管出口处液面高度hC。相应地，积液段的管内平均空泡份额由hC/2确定。

式中：θ为水平管内积液液面与水平方向所成角度；hC为水平管出口处液层高度。

1.2.4 气壁剪切因子

由该水平管的气相单相压降特性实验，确定气相—壁面（简称气壁）剪切因子fWG，从而获得fWG与气相雷诺数ReG的关系

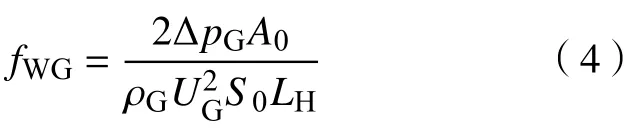
式中：ΔpG为水平管上两取压孔间的气相压差；UG为管内实际平均气速；S0为水平管单相流动湿周；LH为水平管上两取压孔间的距离。

1.2.5 界面剪切因子

将水平管内积液段视为平均高度为0.5hC的滞留液膜（如图4 所示），则积液工况下水平管上两取压孔间气相压降为

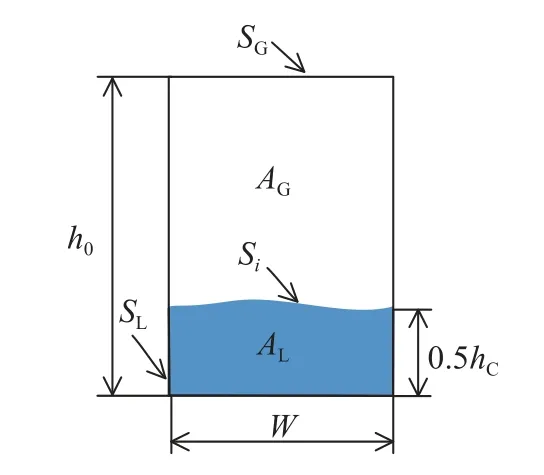
图4 水平管横截面内积液两相分布示意图Fig.4 Schematic of the gas and liquid distribution in the cross-section of horizontal pipes under liquid loading

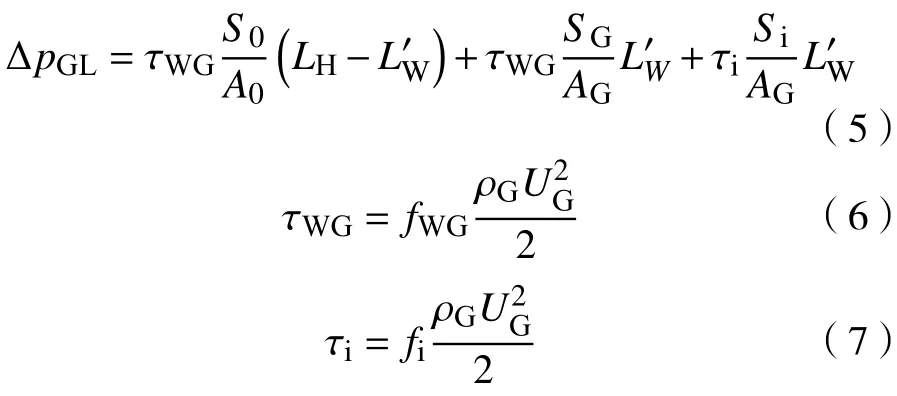
式中：ΔpGL为积液时水平管上两取压孔间的气相压降；τWG、τi分别为气壁、气液界面剪切应力；SG、Si分别为气相与管壁、液相的润湿周界；AG为气相在水平管内的实际流通面积；为压降测量段内的滞留液长，=LW-0.20。

其中，AG为

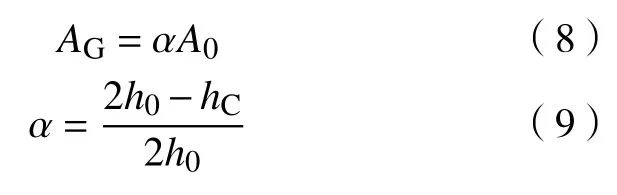
式中：α为水平管积液段平均空泡份额；h0为水平管流道高度。

因而在不同ReG下，根据已知的fWG预测方法、实验获得的LW和θ，可求出界面剪切因子fi。

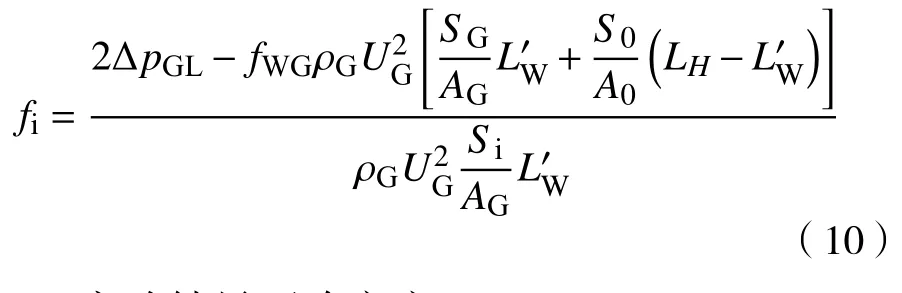
1.2.6 实验结果不确定度

根据误差分析，本文由实验获得的，LW和θ的不确定度见表2。

表2 实验结果的不确定度Tab.2 Uncertainties of the experiment result

2 实验结果及分析

2.1 管内滞留液长实验结果

水平管内滞留液长LW与管内气相Wallis数间的关系如图5。由图5 可见，水平管内积液的存在对应于一个较大范围（0.33～0.55），与垂直管或倾斜管的积液特性明显不同。对气井而言，这意味着＞0.55 时积液被气相排出水平段，在0.33～0.55 时积液在水平段稳定滞留，＜0.33 时积液可倒流进更深的井段。

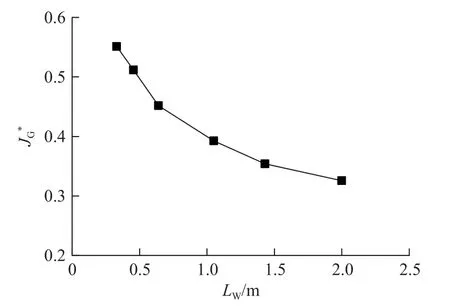
图5 水平管内滞留液长实验结果Fig.5 Experimental results of the liquid length in horizontal pipes under liquid loading conditions

2.2 气壁剪切因子实验结果

气壁剪切因子fWG实验结果如图6。

由图6 可知，fWG随管内气相雷诺数ReG的增大而降低，处于层流至湍流的过渡区。图6 中也示出了Blasius 公式的预测结果，可见本文实验测得的fWG较之Blasius 公式计算结果平均偏低约9%，在Blasius 公式的预测精确度（15%）之内。

对图6 所示结果进行拟合，可得fWG关联式

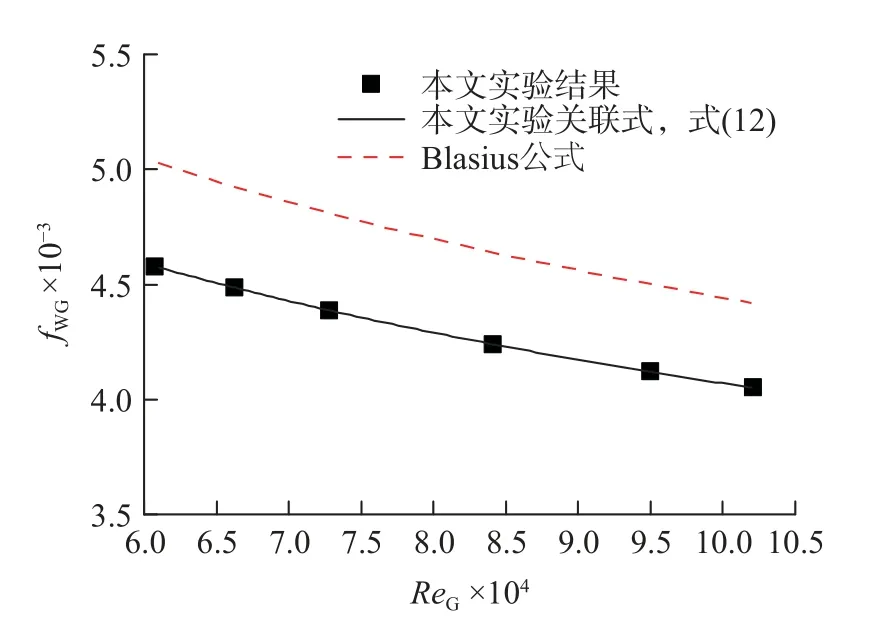
图6 气壁剪切因子实验结果Fig.6 Experimental results of the shear factor between the gas phase and pipe wall

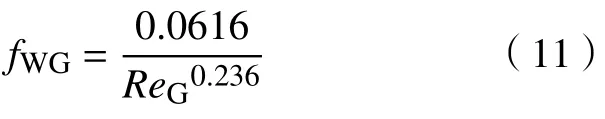
式中，ReG的定义为

式中：Dh为水平管内气相流道的水力直径，气体单相流动时Dh=4A0/S0，气液双相流动时Dh=4AG/(Si+SG)；υG为气相运动粘度。

2.3 界面剪切因子实验结果

气液两相界面剪切因子fi实验结果如图7。由图7 可知，本文实验获得的fi随ReG增大而略有升高；但变化不明显，随ReG由60 988 增大至101 247，fi由0.063 升高至0.108。这因于随管内气速增大，气液两相界面的波动更加剧烈，使fi随ReG的增大而升高。

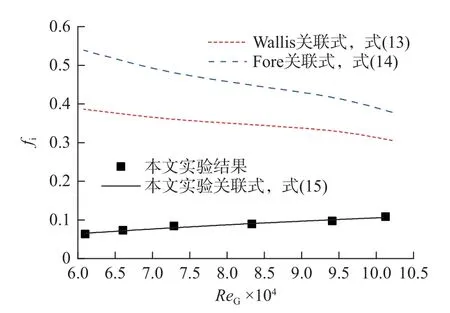
图7 气液两相界面剪切因子实验结果Fig.7 Experimental results of the interfacial shear factor between the gas and liquid phases

图7 中也示出了Wallis等[17]和Fore等[18]基于垂直管内气液逆流CCFL 实验得出的fi关联式

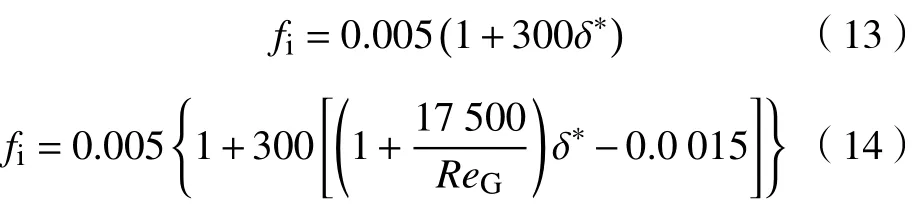
式中：δ*为无量纲液膜厚度，对于圆管δ*=δ/D，对于矩形截面管δ*=δ/h0；δ为管内平均液膜厚度。

由图7 可见，本文由水平管实验获得的fi明显低于这2 个关联式的预测结果，这与水平管与垂直管在积液气速、界面面积、液膜厚度、界面流动行为等方面的不同均有关系。因此，基于本文fi实验结果，提出关联式如下：

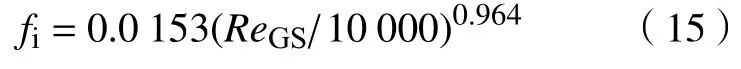
为便于应用，式中雷诺数ReSG的计算采用了表观气速JG和单相流动水力直径Dh0，其定义为

式中，水平管单相流动水力直径Dh0=4A0/S0。

3 理论分析模型的建立与验证

3.1 水平管内积液的液面倾斜机理

除积液工况对应的管内气速范围较大这个特点外，水平管积液的另一重要特征是积液液面呈倾斜状，如图8。与管内CCFL 流动相似，积液工况下，气相为压差驱动流动，液相为重力驱动流动，气液两相通过相界面的切向粘性作用和法向压力平衡互相制约，形成特有的一一对应关系。由于气相压力沿流动方向降低，因而积液液面呈倾斜状。随着JG的增大，气相对液相的曳力增大，同时单位管长的气相压降增大，因而表现为随JG增大，LW减小，液面倾角θ增大。

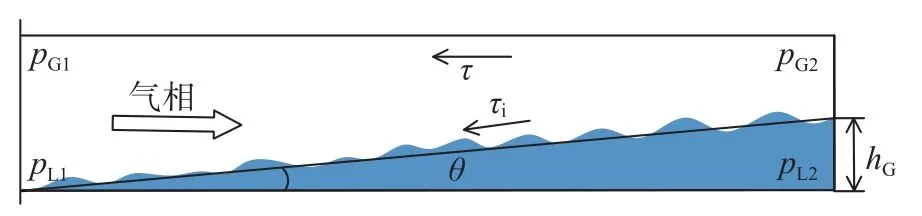
图8 水平管积液时两相流动的受力分析Fig.8 Force analysis of the gas and liquid phases for the liquid loading in horizontal pipes

3.2 水平管积液特性的预测模型

3.2.1 模型的基础方程

为建立水平管内液相滞留长度与气相表观速度之间的理论关系，对积液段两相流动进行受力分析，如图8 所示。将积液段内两相流动视为具有一定液膜厚度的气液分层流动，忽略液相与管壁间的粘性损失，对气、液两相分别建立动量方程，得

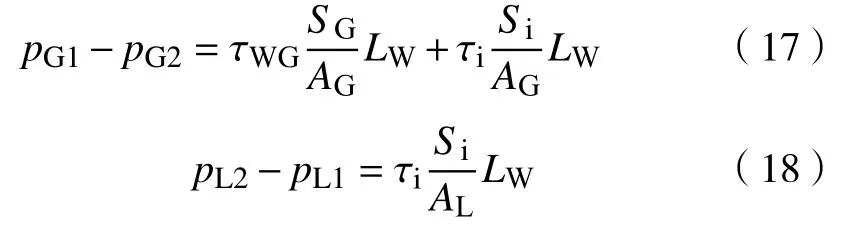
式中：pG为管内气相压力；pL为管内液相压力；AL为管内液相流通面积，AL=A0-AG；下角标1和2 分别表示积液段的进气端和排气端。

由图8 可知，在积液段两端存在如下关系：

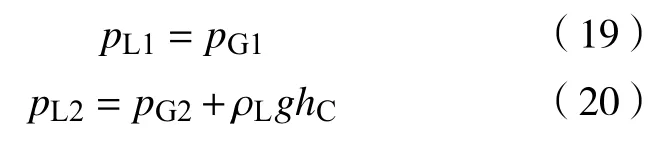
将式（19）、式（20）代入式（18），并进一步和式（17）联立消去压力项，可得

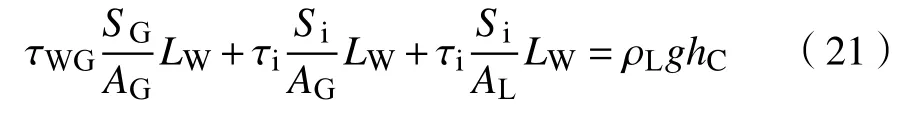
假定液膜厚度在积液段内沿管长线性增大，则积液段内平均液层高度为0.5hC。因而，AG、AL、Si、SG均可由h0、管内流道宽度W及hC表征，如

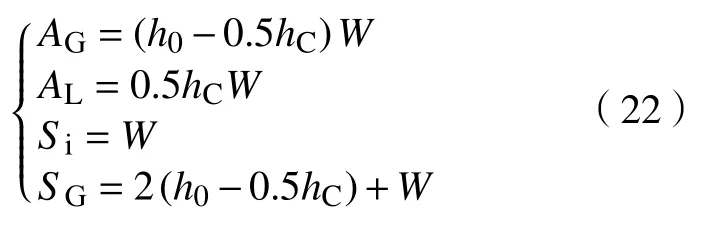
将式（6）、（7）、（22）代入式（21），可得

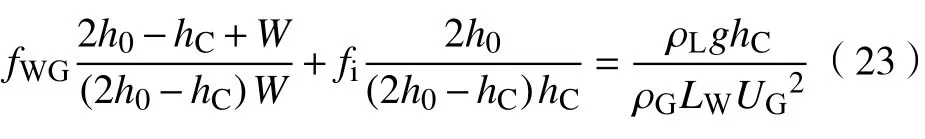
将UG=JG/α代入式（23），得

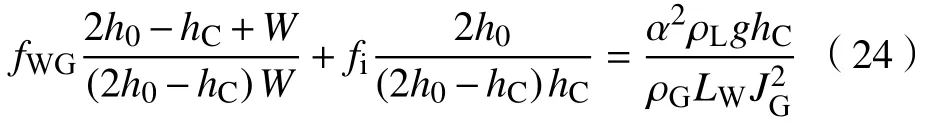
再将式（9）代入式（24）消去α，得

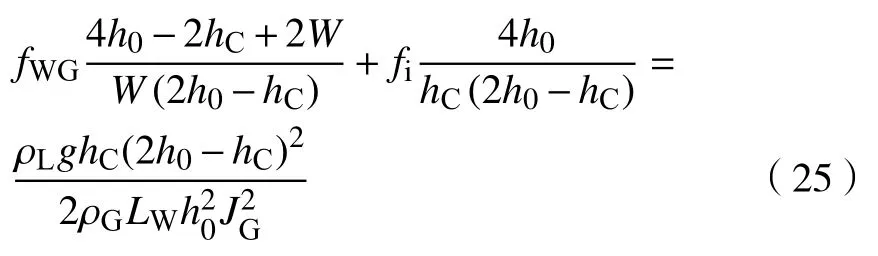
式（25）反映了LW与JG的内在关系，是水平管积液特性理论分析模型的基础方程。

3.2.2 模型的封闭

式（25）中，h0和W为已知结构参数，fWG和fi可通过实验关联式求得，因此对应于每一LW，未知数有2 个，分别为JG和hC。鉴于JG与hC存在一一对应的唯一性关系，基于包络原理，由式（25）对hC求偏导，可得

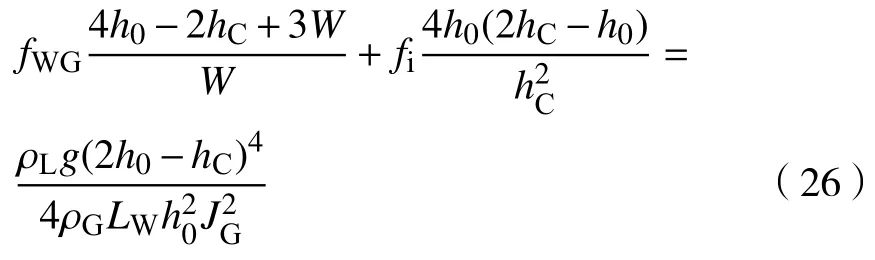
联立式（25）和（26），即为封闭的水平管积液特性理论预测模型。

3.2.3 模型的无量纲化

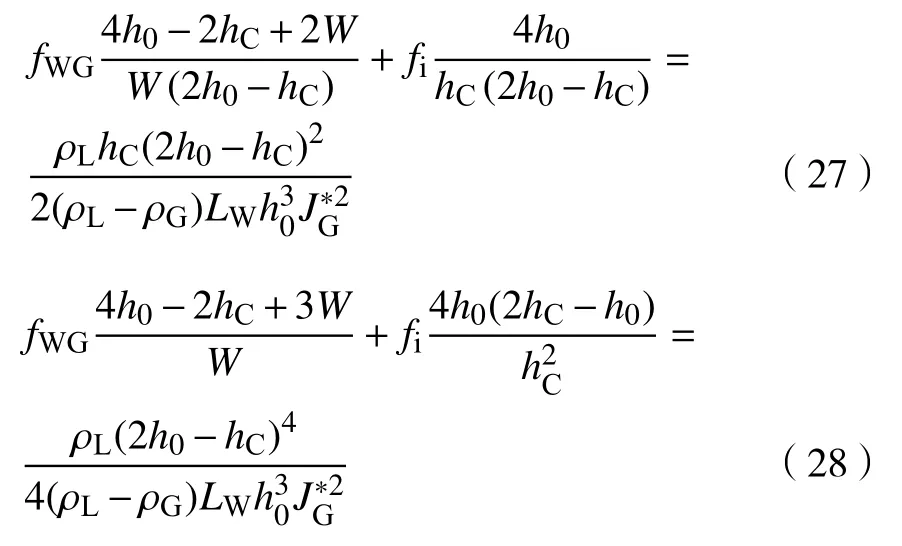
3.3 模型实验验证

基于式（27）和式（28）所示模型，其中fWG和fi分别由式（11）和式（15）确定，对本文予以实验的矩形截面水平管的积液特性进行计算，所得结果如图9 所示。作为比较，图9 中同时也示出了本文实验结果。由图9 可见，本文基于一维两相分层流动建立的水平管积液特性理论模型的预测结果与实验结果间的相对偏差小于8.0%，二者相符良好。因此本文建立的理论分析模型可用于水平管积液特性的预测。本文模型建立是以矩形截面管为例，对于水平圆管，仅区别于AG，AL，Si，SG等结构参数的几何计算方法，读者可自行推导得出水平圆管的理论预测模型。

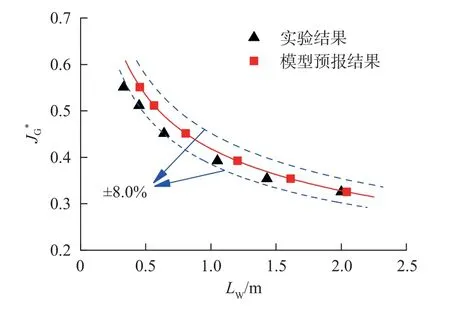
图9 水平管积液特性的模型预报结果与实验结果比较Fig.9 Comparison of the liquid loading characteristics in horizontal pipes between the experimental results and the corresponding predicting results by the proposed model

4 结论

水平管内积液的特点为：管内积液稳定存在对应于一较大的管内气速范围；在该积液气速范围内，积液在管内的滞留长度或积液覆盖范围随气速的增大而减小，但二者并非线性关系。管长2 m的水平管的实验结果表明，其发生积液的范围为0.33～0.55。

气液两相界面剪切因子的大小是建立水平管积液特性理论预报模型的关键参数。本文由实验获得，在水平管积液工况下，气液两相界面剪切因子随管内气相雷诺数增大略有升高，但变化不明显；随雷诺数由60 988 增大至101 247，剪切因子由0.063 升高至0.108。基于本文的实验结果，提出了预测气液两相界面剪切因子的实验关联式。

基于积液液面倾斜机理分析和两相流动受力分析，以及将水平管积液段内两相流动简化为具有一平均液层高度的气液分层流动，根据两相分相流一维分析，获得水平管积液特性，即与LW关系——理论分析模型的基础方程。进而基于包络原理使模型封闭，提出了水平管积液特性理论预测模型。

所提出理论模型的积液特性预报结果与本文实验结果间的相对偏差小于8.0%，二者相符良好，说明该模型可用于水平管积液特性的预测。