流体平移式电卡制冷系统模拟及性能分析

江松轩，韩 华，任正雄，高嘉檠

（上海理工大学，能源与动力工程学院 上海 200093）

传统的蒸汽压缩式制冷技术的卡诺循环效率低，使用的制冷剂对环境有害、噪声大、体积大。根据蒙特利尔协议，考虑发展中国家经济水平和科技水平，以及在当时只有少数国家生产含氯氟利昂的客观情况，协议要求各国在2000 年之前逐步淘汰协议中的化学物质（如氯氟烃类氟利昂（CFC）），氢氯氟烃类氟利昂（HCFC）作为CFC类物质的重要过渡性替代物质，部分将在2030 年前逐步淘汰（如R123）。目前制冷剂的生产主要是氢氟烃类氟利昂，如R134a 或是无氟无氯类冷媒如R600a 等，对环境的破坏较小[1-2]。目前生产的氟利昂虽然不存在破坏臭氧层的缺点，但仍保留了制冷效率低和能耗大的不足，甚至有的还保留了加剧温室效应的缺点或是易爆造成安全问题。因而研究新型节能环保高效的制冷方式意义非凡[3-4]。

基于固态相变热效应的制冷技术作为一种最具希望的替代技术，近几十年受到广泛关注，这种技术采用的固态相变制冷材料会在遇到外部刺激的时候产生温度变化，利用这种温度变化将热量从冷端转移到热端，达到制冷效果。磁卡制冷技术目前发展较为成熟[5-6]，基于磁卡效应实现制冷循环的器件也非常多，但磁卡制冷所需的稀土材料价格高昂[7]，人们开始探索材料更为廉价、绝热温变更高的电卡制冷。

电卡制冷是基于电卡效应的新型制冷方式，电卡效应与磁卡效应相似，施加电场时，材料内部偶极子被极化，从无序化状态转变为有序化状态，温度升高；去除电场时，材料内部偶极子去极化，从有序化状态转变为无序化状态，温度降低，从而实现制冷[8]。电卡效应的大小取决于电卡材料的性质与形状，以及所施加的电场、环境温度等因素。研究表明[9]，对于一级相变的铁电体，存在两种显著的电卡响应（response），均取决于电场的大小。材料一定时，电场是影响电卡效应大小的关键因素。

电卡材料的研究起初源于对罗希盐的研究，1930 年Kobeko等[10]首次在罗希盐中观察到了电卡效应，从而开始了对其的研究历程。1943 年，Hutzenlaub等[11]又成功对其电卡效应值进行了定量测量。在1962 年，Karchevskii等[12]发现电卡效应在其材料居里温度点处达到最大值。在随后的30 年里，人们分别在SrTiO3，PZT，PbSc0.5Ta0.5O3等材料中测得电卡效应并进行定量分析[13-14]。在2006 年，Mischenko等[15]在Pb0.05Zr0.95TiO3薄膜中发现巨电卡效应，在此之前的电卡效应其温升值非常小，仅为1～2 K，巨电卡效应却能达到12 K左右的温升，因而重新引起了新一轮对巨电卡效应材料的研究[16-17]，并推动了人们在薄膜铁电材料方面的研究和电卡制冷器件的发展。

目前测量电卡材料产生的温度变化主要有两种方法：直接法[18]和间接法[19]。直接法通过温度传感器直接测量材料的温度变化，但存在一定的漏电流，不适用于高温环境；间接法则是通过测量材料电滞回曲线、比热容和密度，再由麦克斯韦关系得到温度变化。Liu等[20]在2015 年基于介电常数随温度和电场变化的非线性特征，提出了一种预测电卡效应温升的解析方程，适用于普通铁电体和弛豫铁电体电卡效应的间接测量。

整体上，无机材料导热性能强于有机材料，易于加工制作，块体材料耐电压能力不及有机材料，但可以通过多层结构弥补，达到较大温宽。无机材料中的含铅陶瓷类材料有毒、安全性较差。有机材料导热性能不如无机材料，但产生的绝热温升高、延展性较好、无毒、安全性高，且有机材料的相变温度在室温附近，实用性更高。本文针对目前电卡制冷器件的发展，采用基于三元聚偏氟己烯（PVDF）的三元聚合物弛豫铁电体作为电卡材料，设计了一种流体平移式电卡制冷系统，并对系统性能进行了模拟分析与研究。

1 电卡制冷原理及器件

1.1 电卡制冷原理

图1 为电卡制冷循环与蒸汽压缩式制冷循环的对比图，其中，电卡制冷循环中包含2 个绝热过程和2 个等温过程。

图1 电卡制冷循环过程Fig.1 Cycle of electrocaloric refrigeration

a.绝热极化：电卡材料与冷端分离，被置于绝热环境中同时施加一个突然上升的电场，电场强度从E1变化到E2，导致偶极子的排列顺序一致，紧接着制冷剂的热容量和熵下降（整个过程中制冷剂是绝热的且没有热损失），电卡材料的温度从T0上升到T0+ΔT。

b.热量转移过程：制冷剂与热端进行等温热接触，与此同时电场强度从E2变化到E3，确保制冷剂温度为定值。然后热量从制冷剂传递到热端。整个过程中传递到热端的热量为

式中：Qh为热端吸收热量；Th为热端温度；ΔSh为材料熵的变化量。

c.绝热去极化：电卡材料再次从热端分离，与此同时电场强度从E3变化到E4。偶极子变得无序化，因而制冷剂热容量和熵增加。随着材料与其环境分离（绝热条件），便不存在热量的交换，因此，制冷剂温度下降到T0-ΔT。T0为电卡材料初始温度，ΔT为材料在极化和去极化过程中的温度变化。

d.熵的转移过程：制冷剂与冷端等温热接触，热量从冷端转移至制冷剂，冷端温度冷却到Tc。电卡制冷系统制冷剂从冷端吸收的热量为

式中：Qc为冷端吸收热量；Tc为冷端温度；ΔSc为材料熵的变化量。

1.2 电卡制冷器件

自巨电卡效应发现以后，电卡制冷器件得到了较为快速的发展。Gu等[21]在2013 年设计了一种利用电机驱动材料在冷热端之间进行换热的固体平移式电卡制冷器件；Guo等[22]在2013 年设计了一种流体平移式制冷器件；Gu等[23]在2014 年设计了一种无需外部蓄热器的固体旋转式制冷器件；Wang等[24]在2015 年设计了热开关形式的层叠式制冷器件，并对其进行了实验和理论研究；Ma等[25]在2017 年设计了一种静电驱动的固体平移式制冷器件；Torello等[26]在2020 年设计了一种实现巨大温宽的流体平移式制冷器件；Shi等[27]在2020 年基于文献[23]进行了模拟估算，实现了千瓦级的电卡制冷系统。

图2 为Blumenthal等[28]总结的目前电卡制冷器件的9 种分类。其中，采用层叠式(Cascades)的制冷器件以及主动式电卡蓄冷器(active electrocaloric regenerator）是目前应用程度最高、发展最成熟的电卡制冷技术[28]。

图2 电卡制冷设备的分类[28]Fig.2 Classification of electrocaloric refrigeration device

主动式电卡蓄冷器源于磁制冷中的AMR（active magnetic regenerator），按其传热媒介可分为固体和流体形式，主要以PVDF 等高分子聚合物材料为主。利用传热媒介在冷热端移动，拓展温宽[3]。层叠式电卡制冷器件则是利用电卡材料层层叠加，拓展温宽，主要采用BaTiO3以及PST 系列陶瓷材料[28]。

流体平移式AER 相较于固体平移式AER，减少了系统中的传热单元，避免了传热单元和材料之间的摩擦造成的热损失。流体平移式AER 相较于层叠式电卡制冷器件又具有结构简单、紧凑、制冷量大、温宽大的优点，成为目前电卡制冷器件研究的热点[26]。

2 流体平移式AER 建模

2.1 流体平移式AER 模型

基于图2 中电卡器件的分类以及COMSOL Multiphysics 软件建立了流体平移式AER 系统，研究电卡制冷。图3 为建立的二维模型、三维示意图以及在理想情况下系统的运作原理。电场施加在材料上时，材料升温，AER 内部流体由冷端向热端进行流动，并与材料进行换热，材料将热量传递给流体而降温，流体将热量带向热端；电场移除时，材料进一步降温，AER 内部流体由热端向冷端流动，并再度与材料进行热量交换，流体将热量传递给材料实现降温并与冷端换热，最终实现冷端温度的降低，完成一个电卡制冷循环。

二维流体域矩形长51 mm、宽18.1 mm，由电卡材料组成的圆半径0.45 mm，在流体域内呈50×18 阵列规则排列。同时假设：

a.电极。极化为施加电场的过程，去极化为电场减弱直至消失，乃至消失后材料极化仍在减弱的过程。

b.忽略电畴翻转产生的能量损失以及漏电流引起的损失。

c.固体流体之间的较好的热接触。

电卡材料的圆柱状设计增大了与换热流体之间的换热面积，从而能够提高制冷效率。材料中共计布置8 个温度测点（图3）：冷、热端监测点分别位于矩形左、右侧边界中心处，用于监测冷、热端温度变化，分别计为T1，T8；为观察极化及去极化过程中材料中心、边缘以及附近流体的温度变化情况，分别在冷、热端附近选取第1 列、第9 列中从上起第9 个圆柱形电卡材料进行检测，依次为T2，T3，T4和T5，T6，T7。

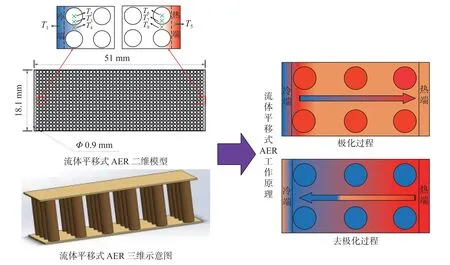
图3 理想情况下的流体AER 系统工作原理以及二维模型Fig.3 The working principle of ideal AER system and the two-dimensional model

矩形的上下边界为绝热无滑移的理想壁面；左端为冷端，设置为外部恒温的对流热通量边界条件，在本模型中可以视为一个理想换热器；右端为热端，同样设置为外部恒温的热通量边界条件，同样可以视为一个理想换热器。

电卡效应归结到微观层面是铁电材料由铁电相转变为顺电相产生相变热，而不同的材料相转变的温度点（居里温度点）不一样，对于铁电驰豫型材料而言则是居里温宽，即所能发生电卡效应的温度区间[29]。本文采用基于PVDF 的三元聚合物弛豫铁电体作为电卡材料，配比为：P(VDF-TrFECFE) 59.2/33.6/7.2 mol%。根据文献[30]中的电滞回线可知，该材料击穿电场强度在300 V/μm 左右，高于一般的块状陶瓷和薄膜陶瓷击穿电场强度；居里温宽（固-固相变点）在300～350 K[31]，接近室温，材料的实际应用更为可行，且聚合物材料施加电场后能够产生巨电卡效应，应用在小型制冷器件以及电介质器件具有很大的优势。

带走热量的流体采用HT-70 全氟聚醚热传导液[22]，该流体只包含碳、氟、氧三种元素，具有优良的介电性能，化学性质稳定，不与PVDF 三元聚合物产生化学反应。材料性质如表1 所示。

表1 HT-70 与PVDF 三元聚合物物性Tab.1 Physical properties of HT-70 and PVDF

图4 为流体平移式AER 一个周期内所施加的电场强度变化以及流体所对应的流速变化。一个周期为0.3 s，在0.05 s 时达到最大电场强度Emax=150 V/μm 并保持到0.1 s，之后电场强度开始减弱，到0.15 s 时电场消失；最大流体流速umax=0.3 m/s，流体在0～0.15 s 时流速先增大后减小，由冷端向热端移动；在0.15～0.3 s 时，流速同样先增大后减小，由热端向冷端移动。理论极化阶段和去极化阶段分别为0～0.15 s 和0.15～0.3 s，因0.1 s 起电场强度开始减弱，将其定义为开始去极化点，将去极化阶段定义为电场逐渐减弱、消失，乃至电场消失后材料中极化程度仍旧在减弱的全过程。因此，实际系统运行中的极化阶段为0～0.1 s，去极化阶段为0.1～0.3 s。

图4 流体平移式AER 中的电场变化及流体流速变化Fig.4 Variation of electric field and fluid velocity in fluid translation AER

2.2 控制方程及定解条件

模拟基于有限元法，式（3）和式（4）分别为Navier-Stokes 方程和连续性方程，描述模型中流体的流动；式（5）和式（6）分别为流体传热方程和固体传热方程。内热源取决于电场的施加或去除，如式（7）所示。二维模型中包含固体域和流体域，固体域中的电卡材料温度变化符合热源方程（式（7））；流体域中流体为不可压缩黏性流体，流动速度及方向受流体流速曲线控制，流体流动及热量传递符合式（3）～（5）。

Navier-Stokes 方程：

连续性方程：

式中：ρf为流体密度；u为流体流速；U为质量流量；µf为流体动力黏度；p为压力。

流体传热方程：

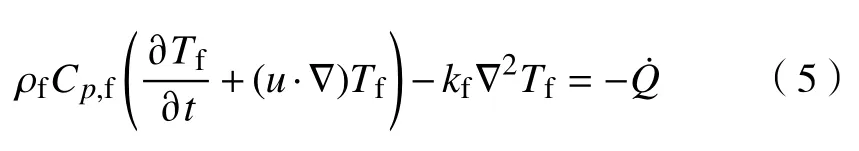
式中：Tf为流体温度；Cp,f为流体定压比热容；kf为流体传热系数。

固体传热方程：

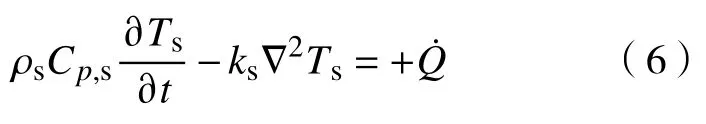
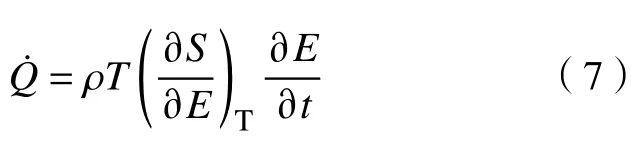
式中：E为外加电场强度；S为熵。

熵与电场之间的关系通常与温度有关，但在实验中，当温度从270～320 K 变化时，该PVDF的电卡效应变化不大，可视为与温度无关[32]，两者关系为[32]

式中：S为材料熵；E为施加电场；C1，C2为实验拟合系数，由材料本身性质决定。对于PVDF 三元聚合物材料，C1=-2.71×10-15J·m2/（kg·K·V2）；C2=-6.85×10-8J·m/（kg·K·V）。

初始温度：

边界条件：

式中：q为热流通量；h为对流换热系数，取为1 629 600 W/（m2·K）。

材料热穿透长度：

式中：ω为电卡制冷器件的运行角频率，满足ω=2f，f为电场频率；δ为材料热穿透长度，代入表1 中数值，可得δ ≤6.9×10-5m。

2.3 网格无关性检验

图5（a）为系统边界和壁面以及材料的网格分布。为了保证结果对网格不敏感，不断细化网格，结果如图5（b）所示，当网格单元数增加到266 015 时，冷端温度基本不随网格数目的增加而变化，取为模拟所用网格数。网格中最小单元质量为0.802，包含边界层、三角形网格、四边形网格及边界壁面网格。平均网格质量为0.878，网格质量良好。

图5 网格细节、边界条件及无关性检验Fig.5 Mesh details,boundary conditions and grid independence test

3 分析与讨论

3.1 流体平移式AER 基准工况性能分析

基于COMSOL Multiphysics 软件，对前述流体平移式AER 进行模拟。基准工况取为：最大电场强度150 V/μm；最大流体流速0.3 m/s；电场频率3.33 Hz（周期0.3 s）；材料厚度根据式（12）取为40 μm；环境温度300.15 K。图6 为冷热端温度分布（T1，T8）以及所取冷热端圆柱形材料中心点、边缘点以及附近流体温度变化（T2，T3，T4和T5，T6，T7），电场强度曲线示于图的下部，方便分析。图7 为不同时刻温度分布云图。T为系统温度。

冷热端温度如图6（a）所示，在0～0.1 s 的过程中电场持续施加在材料上，向热端流动的流体不断与材料进行换热并将热量传递到热端，热端温度T8不断升高，0.1 s 达到最大，近308 K。0.1 s时电场开始减小，去极化开始，材料温度开始下降（图6（b）中T2，T5），而此时直到0.15 s，流体仍然在流向热端（图7（c）-（f）），折损了流体温升，使热端检测温度T8开始下降。0.15 s 时电场消失，流体开始回流，此时冷端才监测到流体温度变化（图7（g），7（h）），在0.19 s 时冷端温度T1达到最低，近297 K。冷热端温差Ts约为11 K（（308-297 K））。此后冷端温度不断升高，在0.24 s左右时材料与流体之间几乎没有温差，冷端温度趋于平稳并最终回到初始温度。

图6 各监测点温度随时间的变化情况Fig.6 Temperature versus time of each detection point

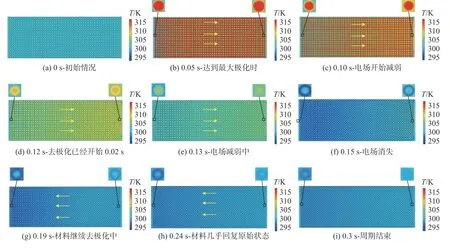
图7 电卡制冷系统不同时刻温度分布Fig.7 Distributions of temperature of the electrocaloric refrigeration system at different times

材料中心温度（图6（b）中T2，T5）变化趋势与电场强度变化趋势一致，因材料导热性能不佳，冷端温度T2与热端温度T5重合，表明材料中心温度未受冷热端流体温度的影响，材料中心未与流体换热，仅材料边缘与流体换热，电卡效应未得到充分利用。热端附近材料边缘温度（T6）与流体温度（T7）曲线在0.12 s 时相交，图7（d）温度云图也可见其相等，之后，T6＜T7，流体仍在流向热端，却由被加热转为被冷却（图7（e）），类似于换热器发生温度交叉时的情形[33]，电卡效应产生的效果被部分抵消。冷端附近材料边缘温度（T3）与流体温度（T4）曲线的交点在0.13 s，图7（e）温度云图也可见其相等，之后，T3＜T4，冷端附近流体开始被冷却（图7（f）），此时电场还未完全消失。0.15 s 电场消失时，冷热端附近材料边缘温度T3，T6及中心温度T2，T5均达到最低。在0.15 s 之后的回流过程中，材料中心温度均高于边缘温度，致使材料边缘一边冷却流体、一边冷却材料中心（图7（f）-（i）），损失部分冷量。

在整个周期中，材料中心最高温度可达到318.50 K，比环境温度高18.35 K。

3.2 不同电场强度下系统冷热端温度变化、制冷量以及冷热端温差

为了进一步研究系统中的变量（电场强度、流速等）对制冷量和冷热端温差的影响，进行变参数模拟。首先，保持其他参数不变，使最大电场强度Emax从25 V/μm 增大 到225 V/μm，步长 为25 V/μm，观察其冷热端温度及制冷量等的变化情况。

图8（a）和8（b）分别为不同电场强度下冷、热端温度变化。

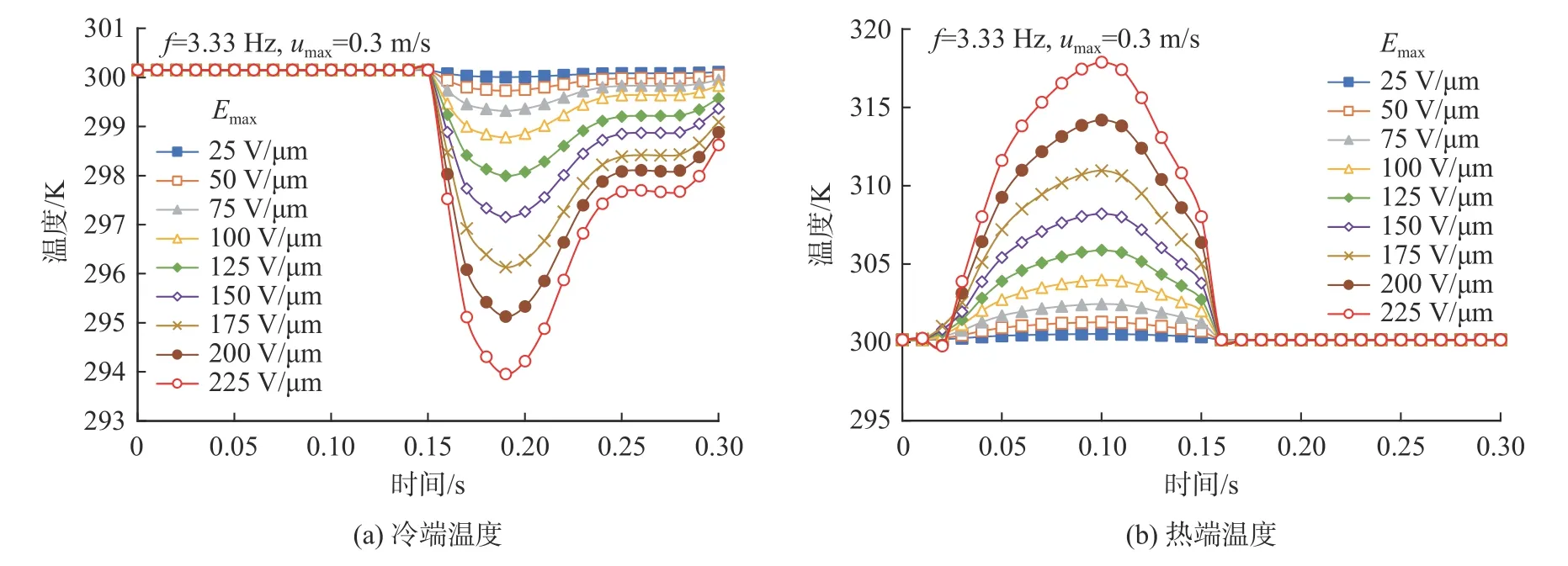
图8 不同电场强度下冷热端温度变化Fig.8 Temperature change of cold end and hot end under different electric field

当电场强度不断增大时，冷端最低温度不断降低，在电场强度大于150 V/μm 后，每升高25 V/μm，冷端最低温度可以降低1 K 左右，在225 V/μm 电场强度下冷端所能达到的最低温度为293.90 K；热端最高温度不断升高，在电场强度大于150 V/μm 后，每升高25 V/μm，热端最高温度可升高3 K 左右，在225 V/μm 电场强度下热端所能达到的最高温度为317.90 K 左右。

图9 为不同电场强度下系统制冷量及冷热端温差变化。系统的制冷量和冷热端温差也会随着电场强度的增加而增大，在225 V/μm 时所能达到的制冷量为10 W，冷热端温差为24 K。在此系统中，制冷量和冷热端温差都会随着电场强度增大而增大，但总体的趋势却并非线性增长，而是二次函数型增长。其中，制冷量Q与电场强度的拟合关系为：Q=0.0002E2+0.01E-0.25，对应的R2值为0.99；冷热端温差Ts与电场强度的拟合关系为：Ts=0.0004E2+0.008E+0.04，对应的R2值为1。

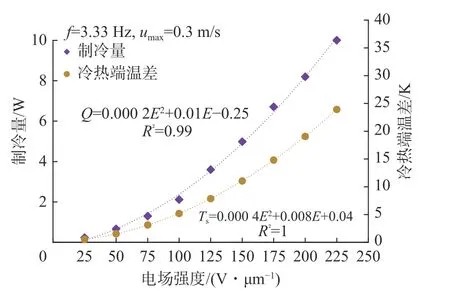
图9 不同电场强度下系统制冷量及冷热端温差变化Fig.9 Variation of cooing power and temperature span between cold and hot ends of system under different electric field

3.3 不同流体流速下系统冷热端温度变化、制冷量以及冷热端温差

保持其他参数不变，使最大流体流速umax从0.05 m/s 增大到0.3 m/s，步长为0.05 m/s，观察其冷热端温度及制冷量等的变化情况。

图10（a）和10（b）分别为不同流体流速下冷热端的温度变化。可见，在流速处于低流速状态时（小于0.1 m/s）系统的冷热端温度变化不同于高流速状态，在低流速状态下冷端会更早达到最低温度，热端会更晚达到最高温度。这是由于流体流速较慢时，流体与材料之间的对流换热效率较低，使得材料与流体之间的换热量较少，所能达到的最低温度高于高流速时所达到的最低温度。

图10 不同流体流速下冷热端温度变化Fig.10 Temperature change of cold end and hot end under different fluid velocities

图11 为不同流体流速下制冷量及冷热端温差的变化情况。可见，系统的制冷量会随着流体流速的增加而增加，在低流速情况下（小于0.1 m/s）的制冷量较小且增长缓慢，当流速大于0.1 m/s 后制冷量会快速变大，几乎呈线性增长。其中，制冷量与流体流速的拟合关系为：Q=20.03u-1.18，R2值为0.99。系统的冷热端温差会随着流体流速的增大而增大，但当流速超过0.15 m/s 后，其增长速度变缓并进一步趋于稳定，但在低流速情况下，增加流体流速会很大程度上提高冷热端温差，其趋势几乎呈指数增长。冷热端温差与流体流速的拟合关系为：Ts=2.27lnu+14，R2值为0.96。

图11 不同流体流速下系统制冷量及冷热端温差变化Fig.11 Variation of cooing power and temperature span between cold and hot ends of system under different fluid velocities

4 结论

采用PVDF 三元聚合物作为电卡材料、HT-70热传导液作为传热流体，在室温环境下（300.15 K），基于COMSOL Multiphysics 软件建立了电卡制冷器件中的流体平移式AER 二维模型，实现了电卡制冷，并进行了变参数性能分析。得出结论：

a.电卡材料导热性能是制约电卡效应发挥的重要因素，导热性能不佳不但导致施加电场时材料热量无法有效传递给流体，而且会发生温度交叉，导致去电场时未有效降温的材料中心与流体抢夺电卡效应冷量的现象。整个周期内，电卡材料中心几乎不与流体换热，电卡效应未得到充分利用。

b.去极化可以理解为电场强度开始减弱、消失，直到材料内部偶极子恢复完全无序的全过程。系统整体的冷热端温度变化受电卡材料电卡效应、导热性能、流体热物性、流体流动速度和方向的共同影响。电卡材料对流体的降温从电场强度减弱到一定程度即开始（0.13 s），并非电场消失后才开始。材料中心温度、与流体直接换热的材料边缘温度均在电场消失时达到最低，冷端流体的最低温度略有滞后。

c.在本系统中，电场强度为225 V/μm、频率为3.33 Hz（周期为0.3 s）时，最大冷热端温差达到24 K（冷端最低温度294 K、热端最高温度318 K），最大制冷量为10 W。

d.制冷量Q、冷热端温差Ts均随（最大）电场强度E的增加而增大，总体趋势呈二次函数型增长，但二次项系数较小。两者回归关系式分别为：Q=0.0002E2+0.01E-0.25（R2=0.99）；Ts=0.0004E2+0.008E+0.04（R2=1.0）。

e.制冷量Q随流体（最大）流速u的增加基本呈线性增长趋势，回归关系为：Q=20.03u-1.18（R2=0.99）；冷热端温差Ts也随u的增加而增大，近似关系为：Ts=2.27lnu+14.07（R2=0.96）。

总之，利用电卡效应实现制冷是一个系统工程，需各个环节有效配合，为使电卡效应得到充分利用，提高材料导热性能至关重要。有机材料虽然电卡效应明显、温升较大，但其导热性能较差，使电卡制冷系统的性能受限。因此，在今后的研究中应综合考虑电场、温升、导热性能、安全性以及经济性，可以设计更加微细的材料形态与器件结构，以弥补导热性能不佳所致电卡效应无法充分利用的不足，或可考虑采用导热性能较佳的无机材料，使电卡效应与导热性能取得较佳平衡，避免出现抢夺冷量的现象。开发导热性能与电卡效应俱佳的材料可从根本上解决该问题。