内埋武器机弹分离相容性及流动控制试验研究

宋 威，艾邦成

(中国航天空气动力技术研究院 空气动力科学中心，北京 100074)

0 引 言

新一代先进有人或无人战斗机一般会配置内埋式武器（多为细长旋成体布局的空空导弹），这不仅能提供空气动力学效率，而且能提高战斗机的机动性能、巡航速度和生存能力[1]。然而，当内埋式武器舱打开释放武器时，弹舱会暴露在载机的高速气流中，从而产生较为复杂的非定常流动现象，如边界层分离与再附、剪切层结构不稳定、激波与激波干扰、激波与边界层干扰等[2]。这些复杂的非定常流动会引起武器上大面积周期性的压力脉动，从而导致作用在武器上的气动力和力矩的不确定性，使得内埋武器机弹分离的运动轨迹和姿态角具有可变性[3]。在内埋武器的质量-惯性载荷比非定常空气动力载荷大的情况下，有效的武器分离通常不是问题。然而，在武器的质量-惯性载荷比非定常空气动力载荷小的情况，由于沿着来流方向逆压梯度的存在，武器穿越舱口剪切层时会产生抬头俯仰力矩，导致武器分离有时会发生俯仰角过大、急速滚转等不相容分离现象[4]。因此，针对内埋武器机弹分离相容性问题开展流动控制研究具有重要的工程应用价值。

正如Coley 和Lofthouse[5]所述：“为判定内埋武器机弹分离相容性，需了解内埋武器的机弹分离动力学特性，当机弹分离出现不相容现象时，可通过主动或被动流动控制方式改变流场来解决”。内埋武器机弹分离动力学属于多体分离动力学研究领域，其主要研究有网格法（包括理论分析、数值模拟和风洞试验等）、风洞CTS 试验和风洞投放试验等[6]。从检索的文献看，目前关于内埋武器机弹分离流动控制的研究方法主要集中在理论分析[7-8]、数值模拟[9-13]、网格测力[14]和风洞CTS 试验[15]上。Sahoo 等[7-8]将内埋武器机弹分离过程分为舱内、穿越剪切层和舱外三个阶段；并基于细长体小扰动理论分析获得导弹低阶气动力和力矩解析解，对弹舱前缘有微射流情况下的导弹分离动力学进行仿真分析，研究微射流的流动控制方式最佳参数。数值模拟主要思路是采用不同方法和网格类型等模拟不同形式的流动控制方程（N-S方程），得到导弹周围的流场和气动参数；将气动参数代入六自由度运动方程（6DOF 方程），在 Δt时间内进行数值积分得到导弹的运动参数，以此重复此过程。如Stanek 等[9]采用RANS-6DOF 方法数值模拟了武器舱前缘稳定喷气射流对内埋武器机弹分离的影响。结果发现，当弹舱前缘施加喷气射流时，武器穿越舱口剪切层时的抬头俯仰力矩会减小或变为低头俯仰力矩。Shipman 等[11]采用LES-6DOF 方法数值计算武器舱前缘稳定吹气对机弹分离动力学特性的影响，并发现前缘稳定吹气对机弹分离的控制效果较好，导弹在分离过程中未出现碰撞载机、姿态角过大等情况。Zhu 等[13]采用DES-6DOF 方法数值模拟了三种不同的流动控制方式（矩形块、棱柱形、楔形块等）对内埋武器机弹分离特性的影响，发现三种流动控制块均能改善内埋武器舱的流动和气动特性，并可增强内埋武器机弹分离安全性。在内埋武器机弹分离流动控制的风洞试验模拟方面，Bower 等[14]采用网格测力试验方法并结合纹影流场显示技术研究弹舱前缘喷气射流对MK-82 炸弹与载机分离动力学特性的影响。结果发现，当弹舱前缘无流动控制装置时，内埋武器在分离过程中出现俯仰抬头，俯仰抬头最大角度达到15°左右，抬头角度过大会对载机安全性产生威胁。当施加喷气射流后，内埋武器出现了低头运动现象。管德会和蔡为民[15]采用风洞CTS 试验手段研究了武器舱前缘布置不同扰流板对内埋武器姿态角的影响，主要关注的是偏航方向。结果表明，不同高度的扰流板可以有效地改善内埋武器舱内的流动结构特性，大大地增加导弹分离的航向安全性。

理论分析、数值模拟、网格测力和风洞CTS 试验等研究手段给定的气动力数据本质上是时间平均或静态的，很难反映机弹分离动态运动过程中的非定常气动力效应。如准定常的风洞CTS 试验是测量分离体在固定位置的时间平均气动力和力矩，利用分离体的质量和惯性信息，通过增量时间步长计算新的空间位置，并重复此过程以实现完整的轨迹模拟[16]。风洞CTS 试验能对机载外挂物分离有很好的预测，但与内埋武器所处空腔流动的特征时间相比，这些空气动力学数据记录的采样率通常要低得多，这样大大地省略了空腔附近流场的任何时间变化。为了更为精确地预测武器轨迹，需要武器上与时间依赖的空气动力学特性，而不是时间平均值[17]。数值模拟在一定程度上像风洞CTS 试验，给定的气动力和力矩是在特定条件下的收敛解，其本质上还是时间平均或静态的气动力。因此，风洞投放试验被国内外研究学者用于内埋式武器机弹分离问题的模拟上，尽管该试验方法在相似设计上有部分缺陷，但在内埋武器机弹分离动力学模拟上具有一定的优势，其能够在动态飞行条件下提供数据，从而反映机弹分离过程的惯性力和非定常气动力效应[18]。如Flora[18]、Merrick[19]、宋威[20-21]等学者采用风洞投放试验研究了内埋武器机弹分离动力学特性，并发现在某些试验条件下内埋武器机弹分离过程出现大幅度俯仰抬头、碰撞载机等不相容现象，但从文献中未见到针对机弹分离流动控制方面的研究工作。

本文采用风洞投放试验方法并结合高速纹影流动显示技术对细长旋成体布局的内埋武器机弹分离流动控制进行探索研究，以期能为未来新一代先进飞行器的内埋式武器的机弹分离系统设计提供被动流动控制方面的些许参考。

1 试验方案及流动控制装置设计

1.1 试验设备、方法和模型

风洞试验在中国航天空气动力技术研究院的FD-12 风洞中开展。FD-12 是暂冲式亚跨超三声速风洞，运行马赫数Ma范围为0.3～4.0，雷诺数Re范围为（1.44～9.48）×106，总压P0范围为（1.2～16）×105Pa。超声速试验段横截面尺寸为1.2 m × 1.2 m。试验段侧壁上有两个观察窗（直径为500 mm），可供观察和纹影仪拍摄流场使用。

载机和导弹模型及武器舱尺寸等与文献[20]中所采用的模型尺寸相同，风洞投放试验方法和高速摄像机的拍摄速度也相同。图1 为风洞投放试验的现场布置图。

图1 试验布置图Fig. 1 The testing diagram in wind tunnel

1.2 被动流动控制装置设计

研究表明，当采用前缘扰流板控制空腔气动声学特性时，前缘扰流板尺寸设计与内埋武器舱前缘来流边界层厚度有关[22]；扰流板高度h与 边界层厚度 δ0相当时，控制效果较好。本文在机弹分离流动控制装置设计上参考此设计思想。

来流边界层位移厚度 δ0用平板湍流边界层厚度

图3 为前缘锯齿扰流板（sawtooth spoiler，STS）和平顶扰流板（flat-top spoiler，FTS）的尺寸示意图，由于载机模型不同导致估算的边界层厚度不同，扰流板的尺寸与文献有所差异。锯齿扰流板和平顶扰流板的高度全部为h=6 mm ， 宽度为w=53 mm，厚度为b=2 mm。其中，锯齿扰流板的锯齿均相同，锯齿距离为l=2 mm ，锯齿角度为 ζ=60°。锯齿扰流板在内埋武器舱前缘的安装示意图见图4 所示，平顶扰流板安装在相同的位置。

图2 平板边界层示意图Fig. 2 Schematic diagram of plate boundary layer

图3 锯齿和平顶扰流板的尺寸图Fig. 3 Dimension of sawtooth and flat-top spoiler

图4 前缘扰流板安装示意图Fig. 4 Schematic diagram of leading-edge spoiler

1.3 俯仰角速度和角加速度的求解方法

为分析机弹分离过程中导弹的俯仰角速度 ω和角加速度 ε变化规律，可采用俯仰角 θ求导的方法得到导弹俯仰角速度 ω和角加速度ε。俯仰角速度 ω采用五点中心差分算法，公式如下：

2 机弹分离相容性判据表达式

为提高外挂式武器（主要为轴对称旋成体）分离的安全裕度，Covert[24]在他的文章中介绍Schoch 提出外挂式武器在t=0.25 s内下降垂直位移Z不小于外挂物的最大半径rm（简称为“Schoch 判据”），其表达式为：

Schoch 判据表达式（4）只给出外挂物垂直方向位移Z的判定，且是基于外挂式武器分离给出的。如果考虑质量重、无精确制导要求的空对地武器分离，姿态变化不是很重要，采用Schoch 判据来判定外挂物分离安全性是合适的。然而，对于轻型化、精确制导和弹射延迟点火的内埋武器机弹分离来说，不仅要求武器在分离后要达到一定的安全距离，且此时武器姿态角也是较为重要的运动参数[25]。内埋式武器的机弹分离过程需要综合考虑载机和导弹系统设计要求，安全性主要是针对载机系统而言，只要导弹到达一定的安全距离不碰撞载机均可认为是安全分离。但若此时导弹的姿态角过大并不有利于导弹导引头锁定目标、控制或点火。因此，机弹分离安全性并不能全部概括内埋武器的分离过程。于是，国外的学者Coley 和Lofthouse[5]指出“aircraft-store compatibility（相容性） during internal weapon separation”更能概括内埋武器的机弹分离过程，但他们并没有给出内埋式武器机弹分离相容性的判据。中国航天空气动力技术研究院宋威积极引入并倡导“机弹分离相容性”概念，并给出内埋武器机弹分离相容性的判据，他指出：对像细长旋成体式空空导弹来说，导弹脱离载机后的0.5s 时间内，导弹下落的垂直位移需满足Z≥10dm，且达到安全距离时刻的俯仰角范围 |θ|≤9°，其中dm为导弹的最大直径。即有如下判据表达式：

由于内埋式武器的气动外形和分离类型种类繁多，该判据并不是通用的，可依据不同的情况进行调整。机弹分离安全性是机弹分离相容性的必要条件，不安全的分离运动一定是不相容的，安全的分离运动也不一定相容。式（5）可作为内埋武器机弹安全性的判据，即当导弹分离后的0.5 s 时间段内的垂直位移满足式（5）可认为分离是安全的，同时若此时的导弹俯仰角满足式（6），即可认为机弹分离是相容的。

3 风洞投放试验结果与分析

3.1 前缘有无流动控制时弹舱流场结构分析

图5 为武器舱前缘有无流动控制装置时，内埋导弹在武器舱内未分离时刻的流场结构。从图5（a）可以观察到，内埋武器机弹分离过程所经过的流场结构非常复杂和杂乱，与载机模型外形复杂有关，但可以主要分为以下几个流动区域：载机激波区Ⅰ；舱口剪切层区Ⅱ；舱内反射激波区Ⅲ；载机激波Ⅰ在风洞底部的反射激波区Ⅳ（飞行器真实机弹分离过程是不存在的，因此导弹在此区域内的运动是无效的）；前缘气流膨胀区Ⅴ。其中，载机激波区Ⅰ是超声速气流受到载机头部滞止减速、压缩产生的斜激波，激波后的压强增大，起到阻碍载机飞行效果。舱口剪切层区Ⅱ是由舱内近似静止流动与舱外高速流动剪切形成的，白色线为舱口剪切层的边缘线，剪切层附着在弹舱的舱口处，沿着风洞的来流方向，舱口剪切层厚度 δs呈现逐渐增大的趋势。舱内反射激波区Ⅲ是由进入武器舱内的气流在舱底反射形成的，区域范围最大。从图5（b）可以观察到：当武器舱的前缘布置扰流板时，在载机激波区Ⅰ和舱内反射激波区Ⅲ之间产生一道由前缘扰流板产生的激波区（扰流激波区Ⅵ）。比较图5（a、b）可以观察到，当弹舱前缘布置扰流板时，舱口附近处的剪切层厚度大于无流动控制装置时弹舱的剪切层厚度，表明前缘布置扰流板具有抬升或加宽弹舱附近剪切层的效果，从而可使得剪切层结构内部的速度梯度减小。

图5 有无流动控制时的弹舱初始流场结构特征Fig. 5 Initial flow field in internal bay with or without flow control

3.2 无流动控制装置时机弹分离结果与分析

图6 为武器舱前缘无流动控制时机弹分离运动图像序列，图7 为对应垂直位移Z、俯仰角 θ的时间历程图。其中，导弹分离时刻初始俯仰角为 θ0=−5°，弹舱长深比为L/D=11.86， 载机攻角为αA=2.2°，试验马赫数为Ma=1.5。 以下曲线中的垂直位移Z和俯仰角θ随时间变化值均为风洞试验数据换算到真实飞行时的数据。

图6 无流动控制时图像序列Fig. 6 Time sequences of images without flow control

结合图6 和图7（a）可看出，当内埋导弹与弹射架解锁分离后，在导弹头部未进入载机激波区Ⅰ前，垂直方向位移基本为线性下降（图7（a）中t≈0 ～0.43 s时间段），当导弹头部碰撞到载机激波区Ⅰ后，导弹头部未能穿过载机激波区Ⅰ，而是沿着载机激波区Ⅰ的内侧边缘向下运动（图6 所示）。该阶段的导弹垂直位移呈弱非线性变化，但仍然是一直向下运动（图7（a）中t≈0.43 s 以后）。当导弹分离时刻为t=0.5 s 时，导弹垂直方向位移为Z0.5=3.21 m，能满足第2 节提出的机弹分离相容条件式（5），导弹分离运动是安全的。从图7（b）的俯仰角曲线可知，当导弹以低头初始俯仰角与载机分离后，导弹俯仰角先非线性增大后减小，当分离时刻为t=0.5 s 时，导弹俯仰角为 θ0.5≈14°，不能满足第2 节提出的机弹分离相容条件式（6）。综上可知，机弹分离过程是安全的，未对载机产生碰撞或威胁，但这并不是一个相容的机弹分离过程，需要采用一定的流动控制技术进行优化。

图7 无流动控制时垂直位移、俯仰角历程图Fig. 7 History chart of vertical displacement and pitch angle without flow control

图8 为导弹俯仰角速度 ω和角加速度 ε的变化规律。俯仰角加速度 ε是导弹俯仰力矩特性的运动学体现， ε的变化能够反映导弹俯仰方向气动特性的变化。

图8 无流动控制时的俯仰角速度和角加速度历程图Fig. 8 History chart of pitch angular velocity and acceleration without flow control

如图8（a）所示，将内埋导弹的分离运动过程分为三个主要阶段：1）阶段A 为导弹分离后到 ε=0的时间段（t≈0～0.32 s），导弹运动区域主要为舱口剪切层区Ⅱ、舱内反射激波区Ⅲ及气流膨胀区Ⅴ；2）阶段B 从 ε=0 时 刻 开 始 到 ω=0 时 刻 为 止（t≈0.32～0.55 s），导弹运动区域主要为气流膨胀区Ⅴ；3）阶段C 为 ω =0开始直至分离过程结束，导弹头部沿着载机激波区Ⅰ内侧边缘滑动。结合图6 和图8（b）可知，导弹穿越舱口剪切层区Ⅱ时，由于来流逆压梯度的存在，导弹质心前部区域处于低压区，导弹后部区域处于低压区，产生了使导弹头部上仰的抬头俯仰力矩（ ε＞0）。当导弹全部穿越舱口剪切层区域Ⅱ后，导弹前半部处于前缘气流膨胀区Ⅴ，导弹后半部处于舱内反射激波区Ⅲ，因而导弹前部处于低压区而导弹后部形成高压区，作用在导弹上的俯仰力矩也为正值，效果是使导弹头部俯仰抬头。随着分离时间的增大，导弹前部处于前缘膨胀区域的面积变大（低压区变大），后部处于舱内反射区域的面积变小（高压区变小），从而使导弹上的抬头俯仰力矩有减小的趋势，但仍然为正值，导弹的俯仰角一直向正方向增大（ θ＞0），如图7（b）所示，俯仰方向加速上仰持续时间约为 0.32 s，在 0～0.32 s 时间段内，导弹的俯仰角速度 ω一直增加，至0.32 s 时刻达到最大值 ωmax，此时刻的俯仰角加速度 ε=0。在分离阶段B 内，导弹一直向远离载机腹部方向运动，当导弹头部遇到载机激波Ⅰ后，由于载机头部激波的阻碍作用，导弹向后运动，此时间段内导弹所受的俯仰力矩为负值，俯仰角加速度小于零，起到俯仰减速的效果，导弹的俯仰角速度不断减小直至反号，但由于导弹具有一定的俯仰角速度 ω，导弹俯仰角仍然一直增大，直至t≈0.55 s 时刻达到最大值，此时刻的俯仰角速度 ω=0（图8（a））。在分离阶段C 内，由于导弹俯仰角速度反号，且俯仰角加速度反向加速，使得导弹俯仰角逐渐变小。

3.3 不同被动控制装置对机弹分离相容性影响

图9 所示为武器舱前缘布置不同被动控制装置时的图像序列，图10 为相应的垂直位移Z和俯仰角θ的时间变化图。试验的来流条件与无流动控制装置时相同。

图9 不同被动流动控制时的图像序列对比图Fig. 9 Comparison of time sequences of images by means of different passive flow control methods

从图10（a）的垂直位移对比图可知，与无流动控制装置相同，在导弹头部未进入载机激波区Ⅰ前，垂直方向位移基本上处于线性下降，且变化趋势基本一致，斜率基本相同（t≈0～0.43 s）。当导弹头部进入载机头部激波区域Ⅰ后，垂直位移Z在t≈0.43 s 时刻出现拐点，之后继续下降，呈现出微弱的非线性变化。其中，弹舱前缘布置锯齿扰流板的导弹分离运动垂直位移斜率最大，平顶扰流板的斜率次之，无流动控制的斜率最小，也即导弹在锯齿和平顶扰流板的流动控制作用下，导弹在t≈0.43 s 以后的下降速度较快些，可能的原因是前缘扰流板产生的扰流激波Ⅵ作用在导弹的质心区域，加快导弹向下运动。

从图10（a）的垂直位移变化曲线可知，当分离时刻为t=0.5 s 时，三种状态下的垂直位移Z0.5均大于2.03 m，满足第2 节提出的机弹分离相容条件式（5）。这表明有无流动控制装置时，导弹均未出现碰撞载机现象，机弹分离是安全的。从图10（b）的俯仰角对比图知，当弹舱前缘布置不同的被动流动控制时，导弹俯仰角均呈现先增大后减小趋势。当前缘布置平顶扰流板时，导弹在分离时刻t=0.5 s 的俯仰姿态角为θ0.5=9.56°，不满足第2 节提出的机弹分离相容性条件式（6），但很靠近机弹分离相容的临界俯仰角|θ|c=9°。然而，当前缘布置锯齿状扰流板时，导弹在t=0.5 s 时的俯仰姿态角为 θ0.5=6.33°，满足第2 节提出的机弹分离相容性条件式（6），机弹分离过程是相容的。这表明，平顶扰流板和锯齿扰流板对机弹分离相容性均有一定的控制效果，锯齿扰流板对平顶扰流板的控制效果好。从图6 和图9（a、b）的机弹分离纹影图可以看出，当导弹头部穿过弹舱前缘扰流板产生的扰流激波区Ⅴ时，扰流激波后的压强会变大，且作用在远离导弹质心的头部区域，会起到使导弹上的抬头俯仰力矩减小的效果，从而使得俯仰抬头减缓，这对机弹分离相容性是有利的。前缘锯齿扰流板产生的扰流激波更靠近载机头部区域，且比平顶扰流板产生的扰流激波要强，前缘布置锯齿扰流板对机弹分离相容性的控制效果比平顶扰流板好些。

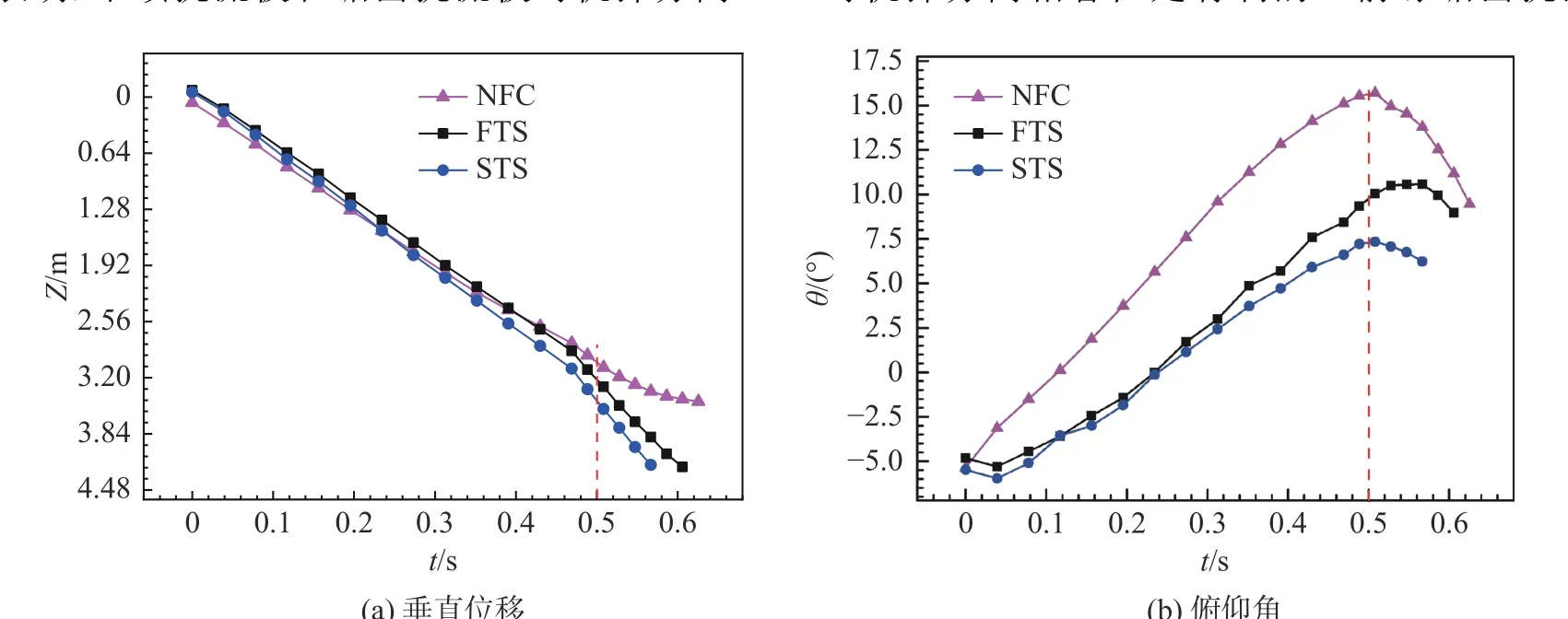
图10 不同被动流动控制时的垂直位移和俯仰角的对比图Fig. 10 Comparison of vertical displacement and pitch angle by means of different passive flow control methods

4 结 论

本文针对细长旋成体布局空空导弹武器的机弹分离相容性问题，通过非定常风洞投放试验方法并结合高速纹影流动显示技术研究了武器舱前缘有无流动控制装置时的机弹分离相容性，被动控制装置采用前缘锯齿和平顶扰流板。可得到以下主要结论：

1）本文指出了机弹分离相容性和安全性的关系，并对细长旋成体布局外挂式武器的机弹分离安全性的Schoch 判据进行改进和完善，提出了针对细长旋成体布局内埋武器的机弹分离相容性判据表达式；

2）前缘锯齿和平顶扰流板能在气流扇形膨胀区域内产生扰流激波，该扰流激波所产生的高压作用在导弹头部能起到减小抬头俯仰力矩的效果，对机弹分离俯仰方向运动产生较大影响，但对导弹垂直位移的影响并不大。

3）前缘锯齿扰流板产生的扰流激波更靠近载机头部区域，且比平顶扰流板产生的扰流激波要强，这导致前缘布置锯齿扰流板对机弹分离相容性的控制效果比平顶扰流板要好。

本研究清晰地显示了内埋武器机弹分离过程中的流场结构变化，对认识机弹分离相容性起到一定的作用，但可惜的是并未能测量到机弹分离过程的动态模型表面的大面积压力分布等更精细化的流场参数，以后可考虑将快响应动态压敏漆（PSP）技术应用到机弹分离问题的研究上，相信会为机弹分离过程中的气动干扰和流场机理分析提供更加精确的流场参数信息。