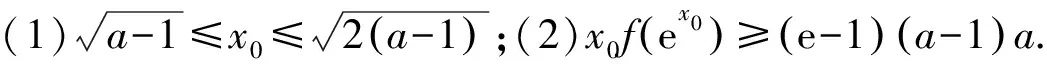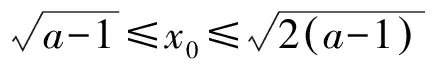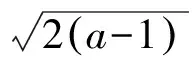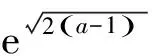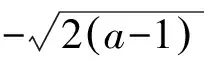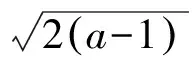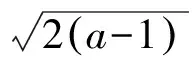构造函数解题教学设计示例

张 昆

(安徽省淮北师范大学数学科学学院 235000)

在探究数学问题解决的思路时，解题主体需要依据数学问题所提供的具体信息特点，从信息中选择相应的要素构成拟似于数学知识点(定义，公理，公式，定理；或者问题现场中所提供的真命题等)结构的信息轮廓，据此，选择使用具体的数学知识点作为范畴性框架，封装信息要素，解决面临的数学问题.这种将外在数学化信息形成拟似于数学知识点结构的过程称为“构造”，运用“构造”的途径探究数学问题解决思路的心理活动过程称为“构造法”.[1]这里举一个高考压轴题的例子，说明使用构造函数解题的教学设计及其课堂实施，其具体途径在于，充分暴露组织问题信息要素形成信息轮廓特点，从信息轮廓特点中萌生出适合于解题的具体函数解析式的心理活动过程.

例1(2020年普通高等学校招生全国统一考试浙江卷理科数学·题22·压轴题)已知1

(Ⅰ)证明：函数f(x)在(0,+∞)内有唯一零点；

关于第(Ⅰ)问的解答略.承认函数f(x)在(0,+∞)内存在唯一零点.

关于第(Ⅱ)问的第(1)小题，笔者实录自己在安徽省庐江中学的教学设计及其课堂实施的关键环节(省略号表示学生思维活动的暂时中断).

师：有价值的想法.那么，如何证明不等式②？

注在探究不等式②及其一类问题的证明思路过程中，使用过去经验形成的数学观念，即在具体函数作为条件的问题中，如果知道了在具体定义域内的函数的单调性，那么要比较两个自变量值大小可以转化为比较这两个自变量所对应的函数值大小而达到目的；反之，要比较两个具体函数值的大小可以转化为比较其中的两个自变量的大小.这是一个观念性问题，更深层次上说，这个数学观念其实来源于函数与自变量之间形成了一对矛盾，矛盾对立面的双方在一定条件下能够互相转化.在以具体函数作为条件的比较相关量大小的问题中，自变量与函数产生的矛盾对立面的转化条件是具体函数在相关定义域内的单调性.这种数学观念学生通过平时学习与解题，已经内化为经验存在于自己的智囊中了，从而面对这类问题时，就可以直接应用了.

师：通过生2的详尽分析，这一问题思路清晰了起来.可惜，生2没有思考出证明不等式④的具体途径，那么如何证明不等式④？

生：……

注(1)格式塔心理学派的创始人韦特海默在其名著《创造性思维》中指出，“产生创造性思维的最大敌人就是，在处理相关信息时，通过回忆过去已经掌握了的知识或某些事实，通过不辞劳苦的态度，盲目地应用学习过了的那些零碎的东西；而不是从信息的本来面目上，从结构上，从结构的要求上统观全局.后者的价值在于，随着结构特点的产生，决定了萌生思维活动的心理矢量，发现信息要素之间的空隙，情境的不完全性，导致有问题之处的具体化从而改变心理矢量.这种心理矢量的地点与方向没有一点是偶然的，所有使用的信息元素，它们不管来自回忆或目前的情境，都是由于信息要素的功能而实现，才进入到这个心理过程之中，它是结构上所需要的，它把初始情境带着空隙以及朦胧的状态转化为明朗的，完整的终极情境状态：一句话，从不完善的格式塔转变为完善的格式塔”[2].

师：非常好.那么如何证明不等式⑥？

注从笔者鼓励学生探究这个问题的解题思路过程中认识到，设出函数⑦只是学生经由长期思考结果的“一朝分娩”罢了.而思考怎样设出函数⑦的心理活动过程，却犹如“十月怀胎”，学生需要从这种“十月怀胎”的思考过滤中吸取各种各样的养分，才能助力于“一朝分娩”.教学设计及其课堂实施必须要注重于这种“十月怀胎”的心理过程，对于寻找函数式⑦与设出函数式⑦这一问题的两个方面，学生所投入的时间与思维资源大相径庭，迥然有别.这就启示数学教师，在教学设计及其课堂实施的过程中，充分暴露了构造函数式⑦的心理活动过程，就是通过不断地启发学生使用过去已经建立起来的数学观念与在某些关键环节中需要萌生新的数学观念的交替过程，完成了探究解题思路任务，萌生与定型了新数学观念，如此才能帮助学生提高构造能力，获得情感皈依.这种构造途径所生成的经验，容易迁移到解题主体面临的信息情境中去，形成具体的数学解题新经验[3].

注这里由于受到篇幅所限，没有实录课堂教学的关键环节.不过，从这个问题的解答实际过程认识到，所构造出函数是对于不等式⑧的一系列探究活动，从而得到了不等式的结果.尽管这里比较详细地写出了证明不等式⑧的逻辑路径，但必须提请数学教师注意的是，在教学设计及其课堂实施中，重在启发学生从将不等式⑧转化为不等式时探究活动的心路历程，这就是将证明不等式⑧的逻辑表达过程转化为学生发现思路的心理发生过程，否则就是将这道题解答的逻辑过程奉献于学生，那很难发挥数学问题解决的教学价值，实现数学解题教学目标.对此，高三数学教师必须思之再思，慎之又慎.

毛主席在其名论《中国革命战争的战略问题》一文中指出，“对于人，伤其十指不如断其一指；对于敌，击溃其十个师不如消灭其一个师”.[4]将这种解决问题时干净彻底的思想应用到指导学生学习数学上来，那就要求数学教师通过教学设计及其课堂实施，帮助学生彻底理解清楚解决一道数学题的想法的来龙去脉与思维的活水源头，这对于教师的施教与学生的学习，都具有十分重要的指导作用.在解题教学中，教师认真地启发学生从问题信息所可能具有结构性特点出发，独立认真地发现问题的思路，例如，在本例探究不等式②的证明思路中，启发学生通过自己思维活动，比较独立地构造函数式⑦，就会促使学生对“构造法”产生良好体验，理解“构造法”探究数学解题的本质要义，为迁移到面临新的问题信息时合理使用“构造法”创造出良好的条件.