改进量子遗传算法在岛礁防空部署问题中的应用

陶 杨， 颜仙荣， 孟田珍

(中国人民解放军92728部队， 上海 200436)

0 引 言

岛礁防空，作为要地防空的一部分[1]，与一般性的要地防空相比，岛礁具有占地面积狭小、分布区域分散、防御纵深缺乏、后勤补给困难、岛外支援有限等特点[2]，易攻难守的问题突出。在岛礁防空任务中，对防空武器的规模数量、布放位置等都有很高的要求，因此，在有限的资源、条件下，如何以尽可能高的效费比，优化部署各类防空武器，达到最优防空作战效果，是亟待解决的现实问题。当前，该类问题的解决主要依靠人工处理，受个人偏好、经验习惯等人的主观因素影响大，为了提高决策的科学性、有效性，本文提出了一种基于免疫操作的自适应量子遗传算法的岛礁防空武器部署优化通用解决方案。

1 岛礁防空问题的数学模型

1.1 岛礁防空区域模型

在进行防空武器部署分析之前，首先，需要设定岛礁防空区域。本文主要综合参考岛礁上的防御要地数量和进攻方可能采用的空袭武器射程，对岛礁防空区域进行划分和设置。不失一般性，假设需要在n个岛礁上进行防空部署，其中，I岛礁有1个主要防御要地和j个次要防御要地，主要防御要地的坐标记为Oi，次要防御要地的坐标记为Oi+k，其与主要防御要地之间的距离为di+k。不妨认为I岛礁防空区域是以主要防御要地Oi为圆心、以进攻方空袭武器射程Di为半径的圆形区域，如图1所示。

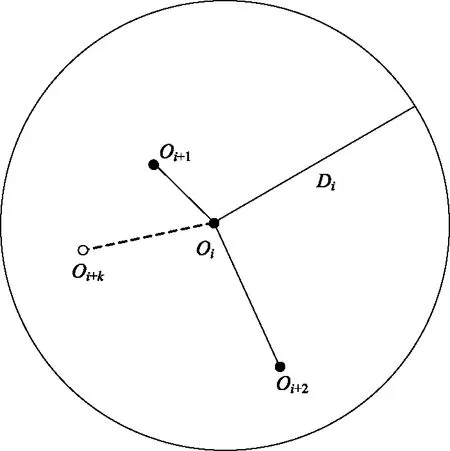
图1 I岛礁防空区域示意图

1.2 岛礁防空武器部署模型

依据设定的岛礁防空区域，建立防空武器部署模型。这里以可部署用于岛礁防空任务的防空武器的成功防御概率和岛礁防空区域的重要程度，构建岛礁防空武器部署函数。为简化问题，假设所有防空武器均部署在防御要地上，即两者之间的欧式距离为0，则第q类防空武器单独完成I岛礁防空任务的成功率为

k=1,2,…,j

I岛礁的重要度Mi为

设第q类防空武器的总数量为Xq={xiq}，I岛礁所有用于部署的r类防空武器共同完成防空任务的成功率为

引入岛礁重要度后，n个岛礁防空任务成功率为

2 岛礁防空武器部署优化方法

经过上述研究分析，该问题可抽象为带约束的目标函数优化问题，可建立如下的适应度函数：

对该类问题的求解，本文给出了一种通用的基于免疫操作的自适应量子遗传算法的解决方案，下面具体就算法实现和算法流程进行说明。

2.1 基于免疫操作的自适应量子遗传算法

量子遗传算法是文献[4]提出的一种改进的遗传算法，该算法融入了量子力学中关于量子纠缠、量子态叠加等理论，对标准遗传算法进行了一系列 “改造”，包括采用量子比特概率幅的形式对染色体编码、通过量子逻辑门对染色体基因演化等，实现了标准遗传算法的“升级”和“进化”，该算法在处理一般的目标优化问题时，也充分显示出了更优于常规遗传算法的效果[5]。但随着应用领域的不断拓展，该算法的弊端也不断暴露了出来，比如：染色体长度一般为固定值，在算法运算初期还未收敛到全局最优解附近时，会因进化不完全导致收敛速度变慢，反之，在中后期收敛后，会因为进化过多导致无效运算增多；量子旋转门的旋转角度一般为固定值，该角度设定过小，算法运算速度会下降，该角度设定过大，计算精度又难以保证，很难一次选中合适的旋转角度；算法在多代遗传获得稳定的最优个体后，整个种群会在其周围不断聚集，很可能造成算法陷入局部最优解而无法跳出等一系列新的问题的出现，也进一步限制了原生算法的使用范围。

鉴于上述出现的诸多新问题，近些年来，也不断有学者提出具有针对性的改进策略，例如：通过融合粒子群算法[6]、调整量子旋转门[7-8]、并行计算[9]提高算法的收敛速度和搜索效率；通过混沌搜索来帮助算法摆脱局部最优解[10]。经过这些改进方法，量子遗传算法的优化性能虽有了一定程度的提高，但计算精度和求解速度不能同时实现、进化过程盲目性较大、种群多样性易丧失等问题却未能完全解决。为进一步克服诸如此的不足，本文提出了一种基于免疫操作的自适应量子遗传算法。

2.1.1算法实现的关键步骤

(1)染色体长度计算

为动态调整算法运算速度，进一步提高运算效率，这里采用了自适应的染色体长度，计算方法如下：

1)设置染色体长度L的初始值为一较小数；

3)比较计算精度与之前预设的许用计算精度tolerance，如果ε>tolerance，则当前的染色体长度L加1后，返回步骤2)，反之，当前染色体长度为合适的染色体长度。

(2)量子比特编码

量子计算主要通过量子比特来完成，作为一种信息载体，量子比特是一种特殊的双态系统，它可以同时处于2个相异的量子态的叠加态中，如|φq〉=α|0〉+β|1〉，其中，|0〉和|1〉分别表示自旋向下和自旋向上态，概率幅常数(α,β)满足归一化条件：

|α|2+|β|2=1

量子比特对染色体进行编码的结果为

(3)量子旋转门

式中：θmax和θmin分别为最大和最小量子旋转门的旋转角度，依据文献[11]给出的旋转角度Δθ∈[0.001π,0.05π]，因此，θmin=0.001π，θmax=0.05π。

(4)免疫操作

免疫算法作为一种新兴智能算法，其基础是生物学中生命体免疫系统，该算法利用免疫系统中的抗体的保持机制和抗体多样性的特征来维持种群的多样性[12]。这里以适应度函数为抗原，以种群个体为抗体，则种群中个体的期望繁殖概率为

其中，

式中：λ为繁殖概率常数；Av为抗原和抗体之间的亲和力，由种群中的个体适应度表征；Cv为抗体浓度；N为种群规模；T为一个预先设定的阈值；kv,s为抗体与抗体之间的相同位数。由公式可知，随着个体适应度的升高，则个体的期望繁殖概率也会越大；当个体浓度增大时，个体的期望繁殖概率反而会越小。通过这种方式，即达到了鼓励适应度高、抑制浓度高的种群个体的目的，也实现了对种群多样性的保护。

(5)种群重建

由于免疫操作的特性，在抑制高浓度的种群个体的同时，也抑制了与抗原亲和程度最高的种群个体，极易造成已经求解得到的最优解的丢失。为了解决这个问题，本文采用了精英保留的策略，实现对计算结果的人工干预，具体操作为在算法中设置一个记忆库，在每次种群更新前，保留当前适应度最高的5个种群个体；在种群更新后，将期望繁殖概率最低的5个种群个体通过灾变操作剔除，并将之前记忆库中的个体补充进当前种群，实现种群重建。这样，即充分利用了免疫操作的优势，又实现了对最优个体的保护。

(6)染色体变异

从断面流速分布的形态变化来看，各级流量下断面流速分布的形态未发生大的变化，流速的变化主要表现为位于弯道的汇流断面的最大流速点位置发生了偏移和流向的变化，但最大流速点位置的变化幅度不大，一般在150 m范围内，而流向的变化一般也在10°以内。

为避免算法无法跳出局部最优，本文引入了量子变异的手段操作染色体变异，具体过程可分为交叉和变异两步：

1)交叉操作。交换概率幅常数(α,β)的值，实现染色体的交叉。由于单点交叉所需的父代染色体之间基因交换的数量较多，易造成对当前优秀种群个体的破坏，所以这里采用双切点交叉的方法，该方法对参与交叉变异的父代染色体基因交换量较少，能够更好地保留优秀种群个体；

2)变异操作。因通常情况下量子比特总会成对出现，所以这里将每对量子比特概率幅常数(α,β)作为一个整体，并随机改变当前染色体中的部分基因序列，实现染色体的变异操作。

2.1.2算法运算流程

在分析了算法实现的关键步骤基础上，梳理算法流程，流程图如图2所示，具体步骤如下：

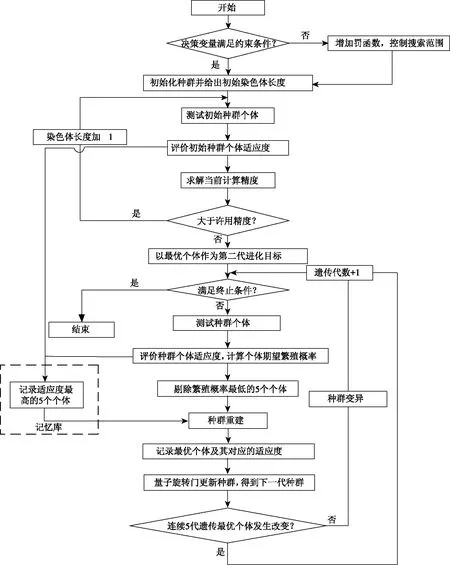
图2 算法流程

步骤1：判断决策变量是否满足约束条件，若满足则继续下一个步骤，若不满足则在适应度函数中增加罚函数，控制决策变量的搜索范围；

步骤3：采用自适应染色体长度的计算方法，得到所需的染色体长度L；

步骤4：判断进化过程是否已达到最大的遗传代数，若是，则输出计算结果，计算结束；反之，则继续下个步骤；

步骤5：从第二代种群开始，通过免疫操作对每个种群个体进行评估，并将期望繁殖概率最高的5个种群个体记录到记忆库中；

步骤6：通过量子旋转门更新种群个体，记录最优个体和适应度，获得新的种群；

步骤7：采用种群灾变和精英保留操作，对种群实施重建；

步骤8：对种群个体实施变异操作，得到子代种群，并返回步骤4。

2.2 算例分析

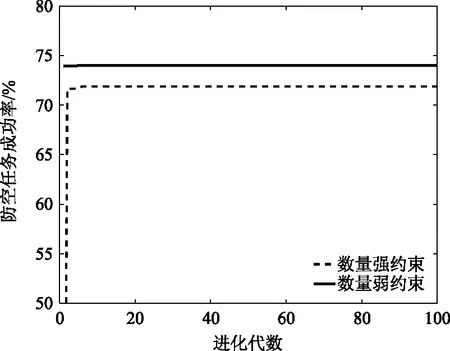
图3 计算结果对比

从自身计算效率来看，该算法稳定性高，计算值收敛不发散。与标准量子遗传算法相比，如图4所示，一是搜索速度快，在进化初期即可以迅速逼近并快速收敛到全局最优解，标准量子遗传算法收敛需要进化56代，而本文算法仅需6代；二是效果更优，标准量子遗传算法得到的防空任务成功率为63.46%，而本文算法的结果为71.90%，计算结果明显优于前者。

图4 标准量子遗传算法与本文算法对比

3 结 语

本文在对岛礁防空问题深入研究的基础上，提出了一种解决岛礁防空武器部署问题的通用方法，具体结论如下：

1)针对标准量子遗传算法的不足，本文提出了一种基于免疫操作的自适应量子遗传算法，该算法采用了自适应染色体长度和旋转门旋转角度，提高了优化效率；引入了免疫操作，淘汰繁殖率低的个体，保持了进化方向正确性，算法的计算效率和稳定性显著提高。

2)引入适应度函数，将多岛礁防空武器部署问题转化为对适应度函数最大值的求解问题，同时，通过增加罚函数来约束防空武器总数量。通过本文提出的智能算法进行优化计算，可以快速准确得到多岛礁防空武器的部署数量需求，经对比分析，证明了该方法的科学性。