基于列流组合的高速铁路列车开行方案编制方法研究

杨 晓

（中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081)

0 引言

截至2021 年底，我国铁路营业里程突破15 万km，其中高速铁路超过4 万km。随着“八纵八横”高速铁路加密成网，跨区省际、省内城际、城郊市域等客运需求呈现多样化发展趋势，要求传统运输组织加快向市场需求导向的根本性转变。而科学的高速铁路列车开行方案编制是提升供给能力与客流需求匹配度的关键所在，对于提升产品供给效率和服务供给质量具有重要意义。

国内相关学者对高速铁路列车开行方案编制进行了深入的研究。张春田等[1]构建了不确定旅客需求下高速铁路鲁棒列车开行方案优化模型，避免列车开行方案备选集合设置不合理对列车开行方案编制质量的影响；董乐谦等[2]提出考虑弧段容量限制的随机用户均衡客流分配策略，并构建双层规划模型，计算得出京沪高速铁路列车开行方案；唐洁等[3]针对高速铁路跨线旅客列车开行方案展开优化研究，建立高速铁路跨线列车开行方案的多目标规划模型，设计该模型的遗传算法；史峰等[4]建立面向旅客服务水平的高速铁路列车开行方案优化的双层规划模型，并将关键OD 对服务列车数约束转化为各车站的停站列车数约束，设计列车停站方案的确定方法；苏焕银等[5]构建了时变需求下高速铁路列车开行方案优化的Stackelberg 博弈模型，并针对京沪高速铁路进行算例分析；张博等[6]引入非集计理论的Logit 模型分析旅客的乘车选择行为，在此基础上建立高速铁路列车开行方案优化模型，协调优化高速铁路列车开行收益和旅客乘车选择满意度；杨宇正等[7]考虑不同时段列车开行方案与客流出行需求量之间的相互影响关系，分析列车开行方案与旅客出行选择之间的主从博弈关系，构建弹性需求下高速铁路列车开行方案优化的双层规划模型，并设计相应的模拟退火求解算法；付慧伶等[8]提出基于“备选集”的高速铁路列车开行方案优化方法，并设计拉格朗日松弛启发算法。

由此可见，以往研究侧重于列车开行方案编制模型和规划方法求解，但对通达性、时效性、便捷性、线路能力、列车载客能力、运输配套能力等研究尚有不足，故重点针对供给能力与客流需求的精准匹配问题，建立列流[9]组合模型，开展高速铁路列车开行方案编制方法的创新研究。

1 列车开行方案的影响因素

高速铁路列车开行方案的优劣取决于供给能力与客流需求之间的匹配度。因此，列车开行方案的影响因素主要包括客流需求、供给能力2 大类。

1.1 客流需求

客流需求由流量、流向、流时、流速等要素组成，是制定旅客列车开行方案的基础，直接影响到列车的开行数量、停站方案等内容。因客流成分、出行目的、经济条件等客流特征不同，客流可被划分为不同层次。不同层次旅客的需求不同，并且呈现日益多样化的发展趋势。在列车开行方案编制过程中，要针对不同特征客流设计差异化列车产品，持续提升列车开行方案的编制质量。

（1）通达性需求。对于高速铁路而言，通达性需求是指通过乘坐高速铁路列车到达某一车站的可达性需求；另一方面，通达性也表现为主要车站节点之间遍历度，即站间服务频率[10]。列车开行方案的服务频率越大，同一方向可供选择的车次数量越多，旅客出行就越方便。

（2）时效性需求。对于乘坐高速铁路列车出行的旅客，时效性需求主要包括全程旅行时间、可得出行时间段2 部分。其中全程旅行时间主要取决于线路运营速度和列车中途停站次数；可得出行时间段受限于列车产品的时间分布属性。

（3）便捷性需求。便捷性需求是旅客乘坐某种交通方式的便利程度。对于高速铁路来说，主要表现为旅客在不同列车之间换乘接续时间，其在列车运行图布线阶段确定。

1.2 供给能力

高速铁路列车开行方案的供给能力主要包括线路通过能力、列车载客能力、运输配套能力。

（1）线路通过能力。高速铁路线路通过能力是线路在单位时间内所能通过的最多列车数量，与列车追踪间隔时间、天窗时长、运行速度差、起停车附加时分、停站时间、停站率等多种因素相关。其中列车追踪间隔时间是关键影响因素之一，应根据动车组牵引制动性能、列车运行控制方式和车站咽喉布置等情况计算确定。

（2）列车载客能力。列车载客能力是列车的最大载客数量，由列车的编组和定员决定。高速铁路动车组主要包括复兴号CR 系列动车组、和谐号CRH 系列动车组，又分为4 辆、8 辆短编组和16辆、17 辆长编组。列车定员由座席位和站席位的总和确定，其中站席位能够反映列车的超员能力。

（3）运输配套能力。列车开行区段设计是编制列车开行方案的必要环节，需要根据各车站联络动车段(所)情况及存放、检修动车组条件来确定。在动车组类型一定的条件下，要求始发站、终到站能够经联络线去往动车段(所)进行存车及运用检修作业。

2 基于列流组合的列车开行方案编制模型

高速铁路列车开行方案编制是多层次多阶段决策问题，基于列流组合法，建立列车开行方案编制模型。

（1）构建OD 客流矩阵。以日均OD 客流密度表数据为基础，建立OD 客流矩阵。假设i，j分别表示起点车站O 的编号、讫点车站D 的编号，研究区段共包含n个车站节点，xij为第i个车站到第j个车站的日均客流量，则OD 客流矩阵Xij为

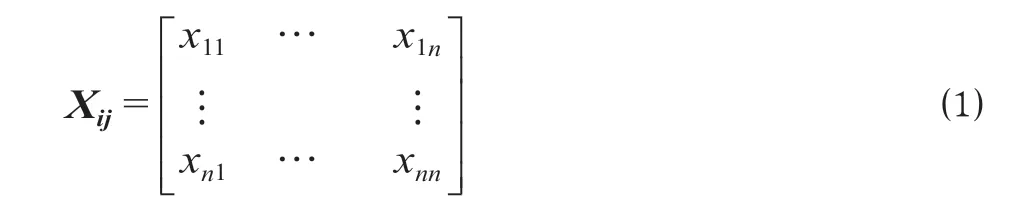
考虑到列车开行方案需要同时满足上下行客流需求，分别提取下行、上行OD 客流矩阵，以此为基础编制下行、上行方向列车开行方案，公式⑵ 至公式 ⑹ 均以下行为例进行阐述。

（2）OD 客流矩阵转化为OD 列流矩阵。假设lij表示第i个车站到第j个车站的OD 列流，α表示列车定员标准对应的客流量，则OD 列流与客流之间转化关系为

下行OD 列流矩阵为

（3）OD 列流矩阵标准化处理。对OD 列流矩阵进行标准化处理，变为n(n-1)/2 行(n-1)列的OD 列流矩阵，下行方向标准化列流矩阵为

（4）构建列车停站方案矩阵，并进行初始化处理。假设r，s分别表示列车种类编号、车站编号，研究区段共包含n个车站节点，对矩阵进行列流组合后生成m类列车，zrs为第r类列车在第s个车站的停站次数，则列流组合后的列车停站方案矩阵为

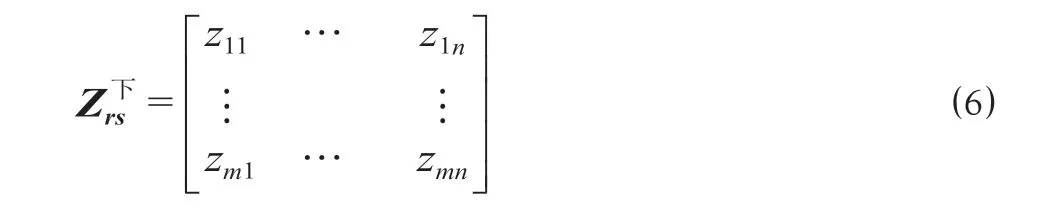
列流组合之前，对矩阵初始化处理，令Zrs=0。

（5）确定列流组合的约束条件。根据各车站联络动车段(所)情况及存放、检修动车组条件，确定列车开行区段。假设Si表示编号为i的车站，Sh，Sp，Sq，Sg分别表示第h，p，q，g个车站，且h≤p、g≥q，Sp-Sq表示第p个车站至第q个车站的区段，Sh-Sg表示第h个车站至第g个车站的区段，若第h个车站、第g个车站能够办理始发终到作业，则列流组合法是第h个车站至第g个车站之间所有Sp-Sq区段列流组合为Sh-Sg区段列车的方法，组合过程中列车停站方案矩阵应满足以下约束条件。

①单个车站总停站次数约束。假设Ss表示第s个车站，所有列车在该车站的总停站次数应不小于车站单日需要办理的最小列车停开作业量，即Ss的总停站次数应不小于车站日均旅客发送量(到达量)除以列车定员标准对应的客运量，该约束可表示为

式中：Qs为第s个车站日均旅客发送量、到达量的较大值，人。

②单列车总停站次数约束。列车旅行速度是列车产品供给效率的重要体现，单列车的总停站次数与列车旅行速度成反比。直达、大站停列车能够提升旅客服务质量，而交替停站、站站停列车能够增强列车产品对沿线客流的吸引力。为兼顾列车开行方案的整体旅行速度和旅客途中上下车实际需求，单列车总停站次数应不大于旅行时间上限的对应的最大停站次数，该约束可表示为

式中：Tr为第r列车的旅行时间上限，min；tr为第r列车所在运行区段上无停站列车的旅行时间，min；t附为列车在车站的起停车附加时分，min；t停为列车在中间站的平均停站时长，min。

③列车开行数量约束，即列车开行数量应不大于研究区段的线路通过能力，该约束可表示为

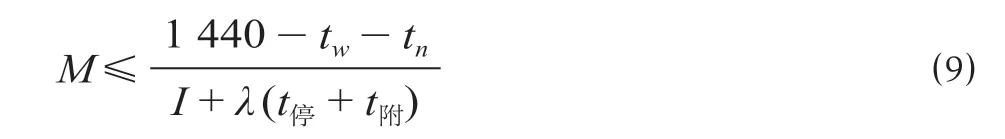
式中：M为列流组合后的列车开行数量，列；tw为综合维修天窗时长，min；tn为无停站列车在第1个站至第n个站之间的运行时间，min；I表示列车追踪间隔时间，min；λ为平均停站率。

（6）依次进行整列流组合、非整列流组合、基于运能适量虚糜的列流组合。

①整列流组合。按照运行区段由长到短、组合节点由少到多的顺序，将中的整列流组合为列车，放入列车停站方案矩阵。假设c为组合节点数量，fc为组合节点的车站编号，f0=1，lfc-1fc表示第fc-1个车站至第fc个车站之间列流，ye为矩阵中整列流按c个节点组合成的第e类列车数量，表示列流组合后第fc-1个车站至第fc个车站之间剩余列流，zefc为矩阵中第e类列车在第fc个车站的停站次数，运行区段S1-Sn的列流按以下公式组合成列车，并更新矩阵。

②非整列流组合。按照运行区段由长到短、组合节点由少到多的顺序，采用“加停站凑整列”方式，将中的非整列流组合为列车，放入列车停站方案矩阵。假设ε为组合节点数量，ℓε为组合节点的车站编号，ℓ0=1，lℓε-1ℓε表示第ℓε-1个车站至第ℓε个车站之间列流，y∂为矩阵中列流按ε个节点组合成的第∂类列车数量，l′ℓε-1ℓε表示列流组合后第ℓε-1个车站至第ℓε个车站之间剩余列流，zeℓε为矩阵中第∂类列车在第ℓε个车站的停站次数，运行区段S1-Sn的列流按以下公式组合成列车，并更新矩阵。

③基于运能适量虚糜的列流组合。按照运行区段由长到短、组合节点由少到多的顺序，采用“加停站与盈亏平衡点判断相结合”的方法，将中的列流组合为列车，放入列车停站方案矩阵。假设ζ为组合节点数量，θζ为组合节点的车站编号，θ0=1，lθζ-1θζ表示第θζ-1个车站至第θζ个车站之间列流，Dθζ-1θζ表示第θζ-1个车站至第θζ个车站之间运行区段长度，D1n为第1 个车站至第n个车站之间运行区段长度，β为盈亏平衡客座率，yδ为矩阵中列流按ζ个节点组合成的第δ类列车数量，表示列流组合后第θζ-1个车站至第θζ个车站之间剩余列流，zeθζ为Zrs矩阵中第δ类列车在第θζ个车站的停站次数，运行区段S1-Sn的列流按以下公式组合成列车，并更新矩阵。经过上述步骤，得出最终的下行方向列车停站方案矩阵。

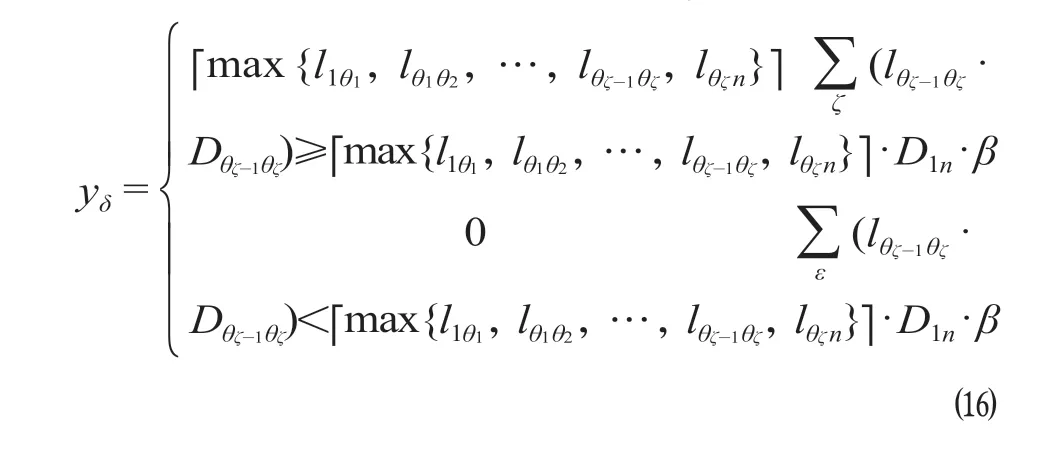
3 实例分析

以某高速铁路A 站—F 站区间为例，研究基于列流组合的列车开行方案编制模型求解及效果分析验证。

3.1 基础前提

（1）客流数据。2019 年A 站—F 站区间下行方向日均客流量如表1 所示。

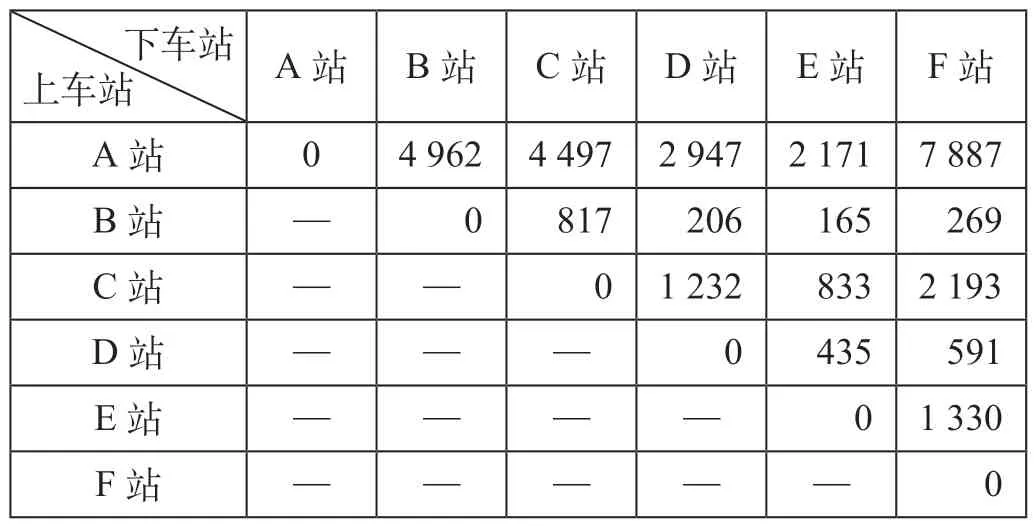
表1 2019 年某高速铁路A 站—F 站区间下行方向日均客流量人Tab.1 Daily average passenger flow in the downward direction of a high speed railway from station A to station F in 2019

（2）相关参数。根据线路实际情况，A 站—F站区间共设6 个车站，A 站—B 站、B 站—C 站、C 站—D 站、D 站—E 站、E 站—F 站的站间距分别为60 km，70 km，90 km，110 km，90 km；A 站、C 站、F 站具备办理客运始发终到作业条件，即列车开行区段为A 站—F 站、A 站—C 站、C 站—F 站。模型相关参数取值如表2 所示。

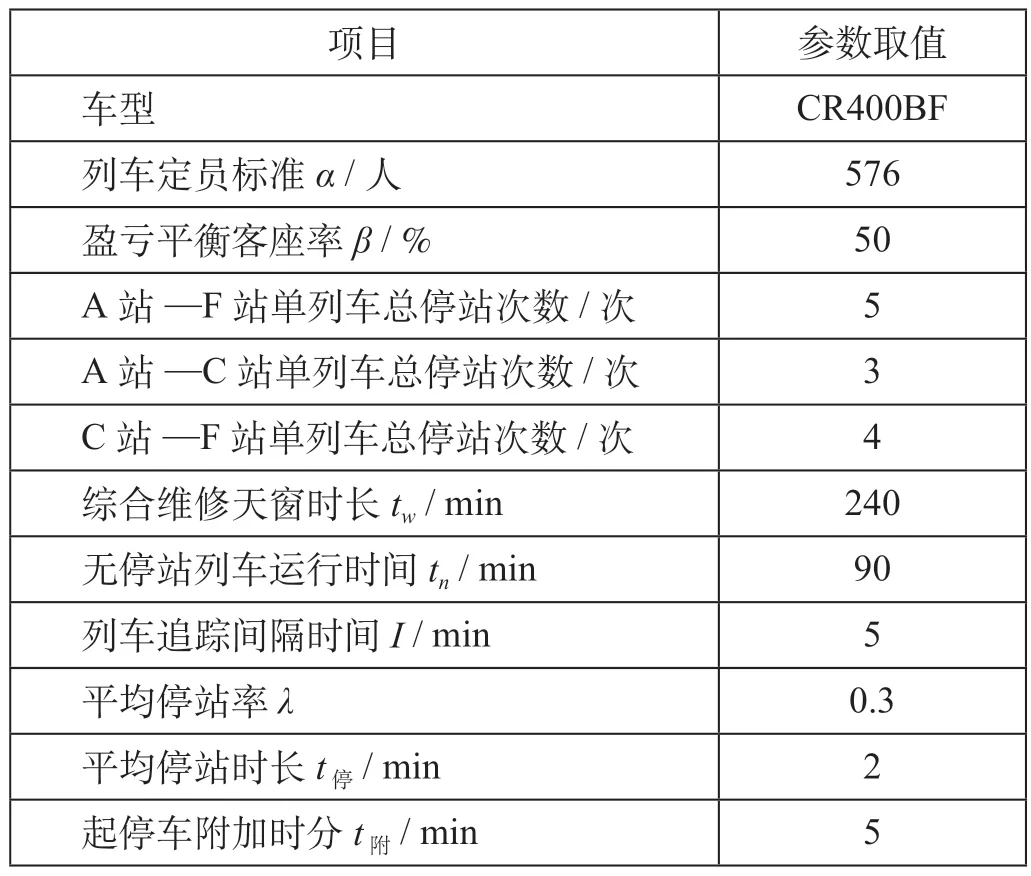
表2 模型相关参数取值Tab.2 Values of relevant parameters of the model

3.2 模型计算

以客流数据和相关参数取值为基础，将OD 客流转变为列流，应用列流组合模型进行列车开行方案编制研究。经计算，A 站—F 站区间列车开行方案结果为：A 站—F站间开行29 列，其中直达列车13列，交替停站列车16 列；A 站—C站间开行5 列，其中直达列车4 列，停站列车1 列，A 站—F 站区间列车开行方案结果如图1 所示。

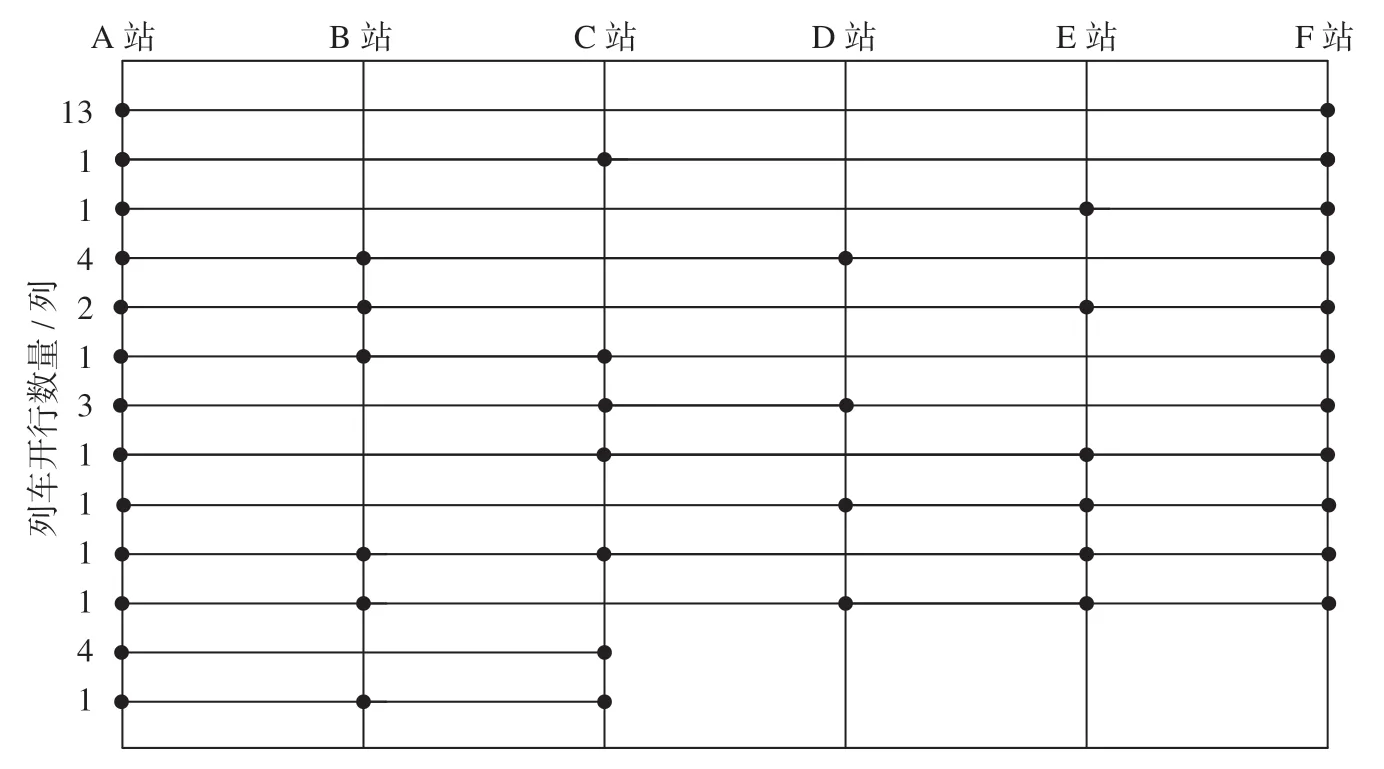
图1 A 站—F 站区间列车开行方案结果Fig.1 Results of train working diagram between station A and station F

3.3 效果分析验证

选取站间服务频率、平均客座率2 项关键指标，对列车开行方案进行优劣效果分析验证。

（1）站间服务频率。列车开行方案的各站间服务频率应不小于站间OD 客流量对应的开行数量需求，可表示为

式中：lij为第i个车站到第j个车站的OD 列流，列；zri，zrj分别为第r类列车在第i个车站、第j个车站的停站次数，次。

（2）平均客座率。平均客座率能够直接反应运力供给与客流需求之间的匹配程度，客座率越接近1，列车开行方案越优，其计算公式为

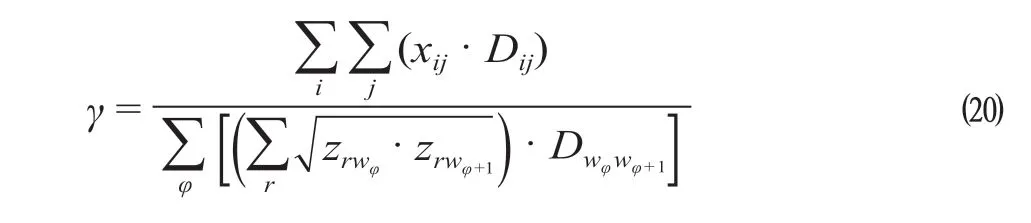
式中：γ表示平均客座率，%；xij为第i个车站到第j个车站的日均客流量，人；Dij为第i个车站至第j个车站的运行区段长度，km；wφ表示第φ个始发终到站的车站编号；zrwφ，zrwφ+1分别为第r类列车在第wφ个车站、第wφ+1个车站的停站次数，次；Dwφwφ+1为第wφ个车站至第wφ+1个车站的运行区段长度，km。

根据A 站—F 站区间列车开行方案结果，计算站间服务频率、平均客座率，得到站间服务频率如表3 所示。

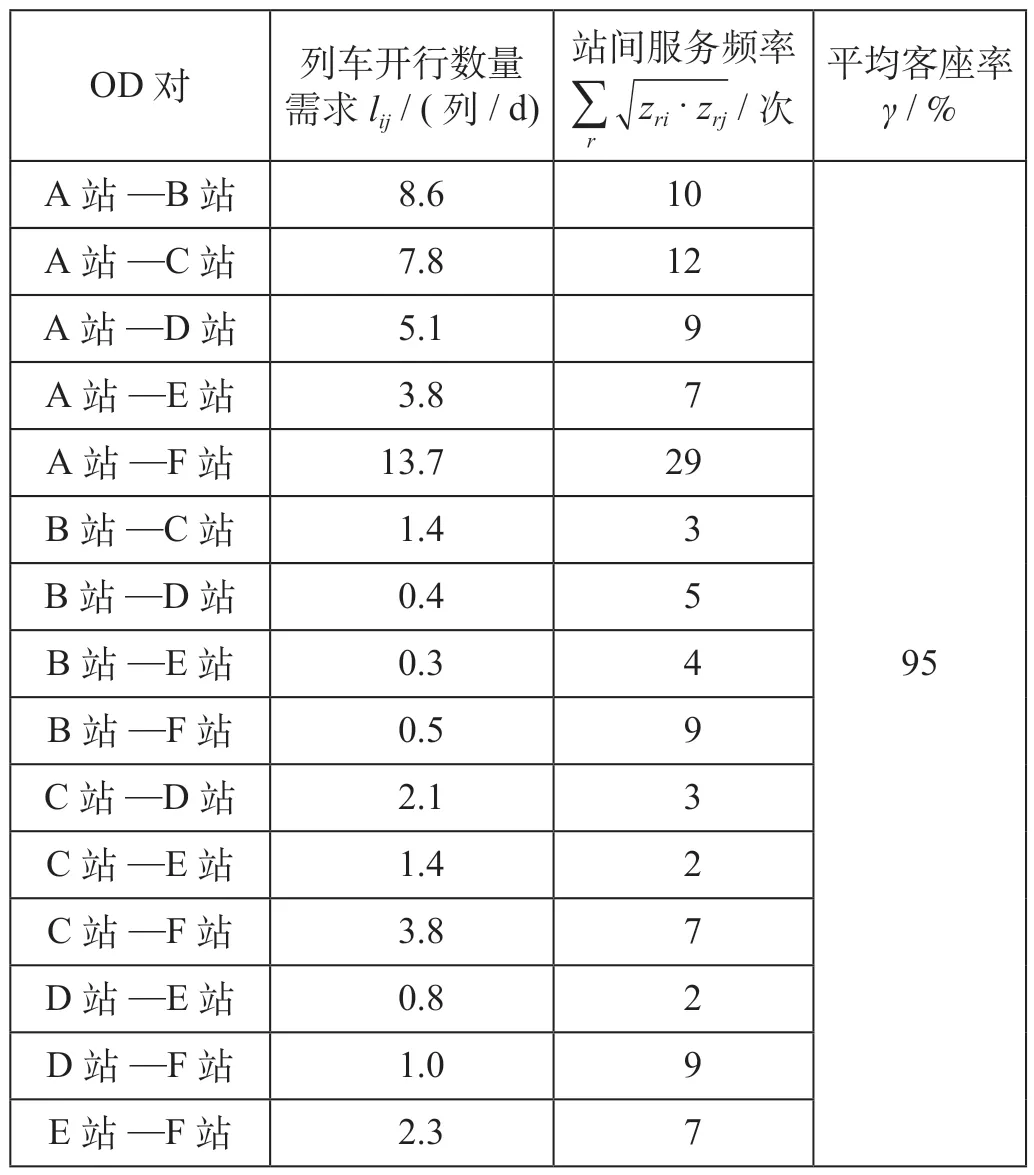
表3 站间服务频率Tab.3 Service frequency between stations

从表3 可以看出，各站间服务频率均大于站间OD 客流量对应的开行数量需求，方案的平均客座率达到95%。因此，该列车开行方案编制结果较优，提出的列流组合模型能够实现列车开行方案与客流需求的精准匹配。

4 结束语

列车开行方案编制是提升供需匹配度的关键所在，研究采用基于列流组合的高速铁路列车开行方案编制模型并进行求解，评判了列车开行方案的优劣。实例验证表明，A 站—F 站区间各站间服务频率均大于站间OD 客流量对应的开行数量需求，方案的平均客座率达到95%，提出的基于列流组合的列车开行方案编制模型及求解方法，在用于编制高速铁路列车开行方案时具有良好的可操作性，可以有效提升产品供给效率和服务供给质量、满足旅客多样化出行体验。后续应进一步深化研究列车开行方案与运行图一体化编制技术，支撑列车产品体系构建。