含LCC-HVDC 的交直流混联电网统一谐波状态估计方法

林晓婉，代 锋，刘沈全，王 钢，曾德辉，吴 为

（1. 华南理工大学电力学院，广东省 广州市 510640；2. 广州嘉缘电力科技有限公司，广东省 广州市 510610；3. 中国南方电网科学研究院有限责任公司，广东省 广州市 510663）

0 引言

为解决中国能源供需地理位置逆向分布的矛盾，中国大力推动基于电网换相换流器的高压直流（line commuted converter based high voltage direct current，LCC-HVDC）输电工程建设，以实现电能跨区域调配，这使中国输电网络逐渐演变成含大规模LCC-HVDC 的交直流混联电网［1］，谐波与谐振问题日益突出［2］。

正确获取电网谐波状态是电网谐波治理的基础，常用的方法是谐波状态估计，即已知电网拓扑结构以及网络参数信息，根据有限量测点所获得的量测数据，通过网络分析建立模型，估算出电网的谐波状态［3］。利用数据采集与监控系统所测的支路功率、节点注入功率建立非线性谐波状态估计模型［4］，求解过程烦琐，且波形畸变时无功功率定义不明确，存在量测量不合理的问题。以全球定位系统（global position system，GPS）同步技术为基础、同步相量测量单元（synchrophasor measurement unit，PMU）为核心的广域测量系统可实时获取母线电压、线路电流相量信息，由此建立的线性谐波状态估计模型求解速度大大加快［5-6］。基于广域测量系统，学者们提出了改进量测量编号顺序［7］、考虑相序特性［8］、划分可疑节点和非谐波注入节点［9］等方法对谐波状态估计模型进行改进。在算法方面，文献［10］对各次谐波状态估计模型采用并行运算以提升运算速度；文献［7，11］在考虑参数误差和测量误差的基础上，改进了最小二乘算法；文献［12-13］基于大量样本数据建立了谐波状态估计的人工智能算法；文献［14］采用动态谐波状态估计算法，快速跟踪系统变化；文献［15］在网络阻抗参数未知的前提下，将盲源分离（blind source separation，BSS）理论应用在谐波状态估计中，文献［16-19］从收敛速度、分离效果等方面改进了BSS 算法。然而，上述研究均面向交流电网，仅将非线性负荷和LCC-HVDC 输电系统视为注入交流电网的谐波电流源，若应用在交直流混联电网，将不能充分考虑交直流系统间紧密的谐波相互作用［20］，难以获取谐波的全局分布规律与关联特征。

LCC-HVDC 输电系统引发的谐波问题具有宽频带特征，而常规的PMU 侧重于工频信号量测，不能满足谐波量测需求。因此，近年来广域宽频同步监测系统得到重视［21-22］，其宽频同步相量测量单元（broad-band synchrophasor measurement unit，bPMU）可同步获取精确的电网宽频量测数据。另外，为降低量测系统成本，在保证电网谐波状态可观性和估计精确性的前提下，研究bPMU 优化配置方法，可提升监测系统的工程实用性。常用方法包括数值法和拓扑法：基于数值法的量测优化配置方法要求量测矩阵满秩，如序贯搜索法、线性无关排序法［23］、自适应遗传算法［24］等，计算量较大；基于拓扑法的量测优化配置方法是根据母线间的相关性判断配置方案是否可观，采用正余弦优化算法［25］、博弈演化算法［26］、改进粒子群两阶段算法［27］、改进自适应帝国竞争算法［28］等进行求解，加快了优化速度。但是，现有研究成果只针对交流电网的谐波状态可观性，其可观性约束和优化配置方法不适用于含LCC-HVDC 的交直流混联电网，因此，必须首先建立电网换相换流器（line commuted converter，LCC）直流母线的可观性约束，才能进而提出综合考虑量测系统成本和谐波状态估计效果的交直流混联电网bPMU 优化配置方法。

因此，本文针对含LCC-HVDC 的交直流混联电网的谐波问题，将交直流混联电网视作有机整体，提出统一谐波状态估计方法。首先，基于LCC 动态相量模型建立其直流系统量测方程，建立交直流混联电网统一谐波状态估计模型，以反映交直流系统间的谐波耦合机理；其次，提出交直流混联电网可观性约束，进而提出计及经济性、冗余度和鲁棒性的bPMU 综合优化配置模型和分阶段求解方法，在保证谐波状态估计效果的前提下，降低量测系统的成本；最后，利用MATLAB 编写统一谐波状态估计程序，实现谐波状态估计值的计算，并与基于PSCAD/EMTDC 仿真平台的仿真结果进行对比，验证其可行性和估计精度。

1 谐波状态估计模型

1.1 母线电压量测方程

量测设备对安装处母线i的电压相量进行量测，即为母线的电压量测，其量测方程为：

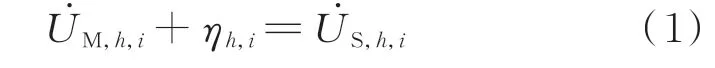
1.2 支路电流量测方程

量测设备对安装处母线i相连的支路电流进行量测得到支路电流相量，即为支路电流量测。基于图1 所示的输电线路或变压器支路的谐波模型，其量测方程为：

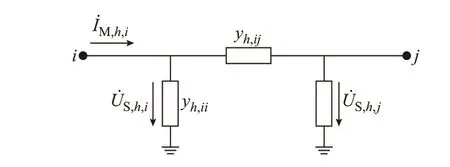
图1 支路谐波模型Fig.1 Branch harmonic model

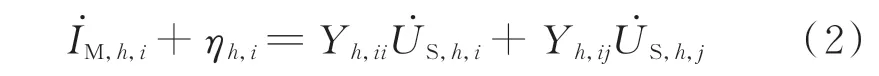
式 中：Yh，ii=yh，ij+yh，ii，Yh，ij=-yh，ij，其 中yh，ii为 支路i侧h次 谐 波 导 纳，yh，ij=1/zh，ij，zh，ij为h次 谐 波 阻抗为母线i流入支路的h次谐波电流相量的量测 量；、分别为待求解的母线i、j的h次谐波电压状态量。

1.3 LCC-HVDC 输电系统量测方程

LCC-HVDC 输电系统至少由2 个换流站和换流站间的直流输电线路组成，换流站主要包含换流变压器和换流器等设备，如图2 所示。在交直流混联电网中，交直流系统间存在着强非线性耦合关系，且在实际工程中bPMU 量测装置一般安装于交流电网中，要实现其统一谐波状态估计就必须建立能表征交直流系统间谐波相互耦合及传变特性的量测方程。动态相量法［29-30］基于换流器的调制理论建立三相开关函数和调制关系式，在沿时间轴变化的固定长度时间窗里对调制关系式进行傅里叶变换，将其转为动态相量形式。它可以准确描述换流器交直流系统间的谐波传变关系，具备物理意义明晰、计算复杂度较小、计算精度高等优势。因此，本文基于动态相量法建立LCC-HVDC 输电系统量测方程。

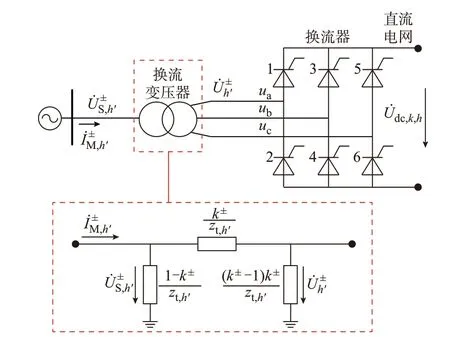
图2 LCC-HVDC 输电系统结构示意图Fig.2 Schematic diagram of structure of LCC-HVDC transmission system

根据图2 所示的换流变压器支路正、负序谐波模型，换流变压器阀侧h′次谐波正、负序电压可表示为：

LCC 直流母线电压udc和换流变压器阀侧电压ua、ub、uc满足：

式中：sua、sub、suc分别为a、b、c 三相电压开关函数，在换流阀的导通、换相和关断状态下，分别取值为1、0.5 和0，正常稳态下三相电压开关函数依次滞后2π/3。

对开关函数进行傅里叶变换，可得三相电压开关 函 数 的 各 阶 动 态 相 量、、。由 于 零 序分量对直流系统谐波没有影响，可将式（4）表示为含正、负序分量的动态相量形式［29，31］，即LCC 直流母线k的h次 谐 波 电 压U˙dc，k，h和 换 流 变 压 器 阀 侧 电 压满足：

联立式（3）和式（5），可对LCC 直流母线k的0至hdc次谐波电压状态量建立LCC-HVDC 输电系统量测方程：

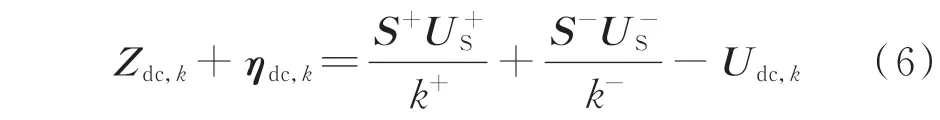
式中：

考虑到计算精度及计算量，取hmax=49、hdc=48。Udc，k为LCC 直流母线k待 求解的0 至hdc次谐波电压状态向量；U±S为待求解的换流变压器网侧-hmax至hmax次正、负序谐波电压状态向量；ηdc，k为0至hdc次 谐 波 量 测 量 的 误 差 向 量；Zdc，k为LCC 直 流 母线k的0 至hdc次 谐 波 量 测 向 量；I±M为 换 流 变 压 器 网侧-hmax至hmax次正、负序谐波电流量测向量，Zt为换流变压器谐波阻抗矩阵；S±为交流侧正、负序网与直流系统间的谐波电压传递矩阵，由电压开关函数的各阶正、负序动态相量组成。

1.4 统一谐波状态估计模型

根据交直流混联电网网络结构、元件参数及bPMU 量测量，综合母线电压量测方程（1）、支路电流量测方程（2）和LCC-HVDC 输电直流系统量测方程（6），可建立线性统一谐波状态估计模型：

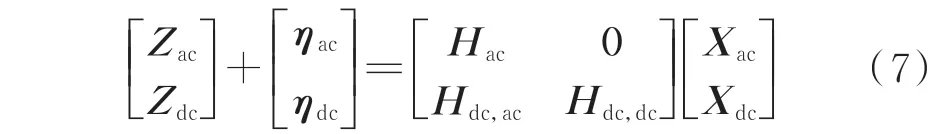
式中：Zac和Zdc分别为交流谐波量测量的Mac维观测向量和直流谐波量测量的Mdc维观测向量；ηac和ηdc分别交流谐波量测误差的Mac维列向量和直流谐波量测误差的Mdc维列向量；Xac和Xdc分别为待求解交流谐波状态量的Nac维列向量和直流谐波状态量的Ndc维列向量，一般选用各个母线的谐波电压；Hac为交流谐波量测量与交流谐波状态量之间的Mac×Nac量测矩阵；Hdc，ac为直流谐波量测量与交流谐波状态量之间的Mdc×Nac量测矩阵；Hdc，dc为直流谐波量测量与直流谐波状态量之间的Mdc×Ndc量测矩阵，由此构成交直流混联电网谐波量测矩阵H。

根据图3 所示的谐波状态估计模型对比图可知，现有的谐波状态估计仅针对交流电网，而本文提出的方法将含LCC-HVDC 的交直流混联电网统一在一个线性模型中进行谐波问题研究，不仅能全面地估计交直流混联电网的谐波状态，还能在物理概念上清晰反映交直流系统的谐波相互作用。

图3 谐波状态估计方法对比Fig.3 Comparison of harmonic state estimation methods

基于上述模型求解，即可通过有限的量测数据估算电网谐波状态。考虑到可能存在的量测粗差，本文采用基于IGG Ⅲ权函数的抗差最小二乘估计［10］进行迭代求解，相比最小二乘估计法，该方法对量测粗差的容错能力更强，计算精度更高。

2 bPMU 综合优化配置建模与分阶段求解方法

本章提出直流系统可观性的评估方法，改进了交直流混联电网统一谐波状态估计的可观性约束集合；进而，考虑量测系统的经济性、冗余度和鲁棒性，建立适用于交直流混联电网的bPMU 综合优化配置模型，并提出相应求解方法。其中，经济性和冗余度指标只与电网拓扑结构相关，较易计算；而鲁棒性指标需计算具体量测矩阵的条件数，计算量显著高于前两者。因此，综合考虑计算量和优化效果，本章提出分阶段求解方法，在Ⅰ阶段仅考虑经济性和冗余度筛出方案备选集，再在Ⅱ阶段增加考虑鲁棒性指标，确定最优方案。该方法可以减少需要进行鲁棒性指标计算的个体数，在保证优化效果的前提下，减小运算量。

bPMU 综合优化配置建模及分阶段求解方法的具体步骤如下：

1）基于量测量和状态量的相关性，考虑N-1准则，建立交直流混联电网的可观性约束；

2）考虑量测成本和冗余度，建立Ⅰ阶段优化目标函数，采用下文所提的改进多种群遗传算法（multiple population genetic algorithm，MPGA），选定目标函数最优的nmax个方案，构成配置方案备选集；

3）综合考虑量测成本、冗余度和鲁棒性指标进行Ⅱ阶段优化，在所筛选出的备选方案中，确定一组最优量测配置方案。

2.1 节至2.4 节分别对上述步骤及改进MPGA进行了详细阐述。

2.1 交直流混联电网的可观性约束

bPMU 优化配置必须满足交直流混联电网的完全可观性；同时，为满足电力系统线路的N-1 准则，要求任一线路发生故障时，电网谐波状态仍然完全可观。因此，基于量测方程（1）、（2）、（6）中量测量与状态量的相关性，考虑N-1 准则，可对含nac个交流母线和ndc个LCC 直流母线的交直流混联电网构建母线可观性约束关系式。

2.1.1 交流母线的可观性约束

对于第i个交流母线，可观性约束关系式为：

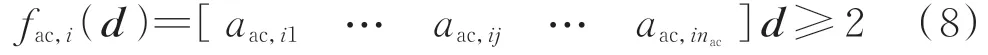
式中：fac，i(d)≥2 表示考虑N-1 准则下交流母线i可观；d=[d1，d2，…，dnac]T是一组二进制编码的nac维向量，当量测装置配置在母线i时，di=1，否则，di=0；aac，ij表 示 考 虑N-1 准 则 的 交 流 母 线i和j之间的关联系数，按式（9）所示原则取值。

式（8）的物理意义为：如果母线i装配有量测装置，或与母线i相连的至少两个交流母线装配有量测装置，则母线i谐波状态可观。

2.1.2 直流母线的可观性约束

在现有技术条件下，LCC 直流母线无法安装bPMU 装置，因此，对于第k个LCC 直流母线，可观性约束关系式为：

式 中：fdc，k(d)≥2 表 示 直 流 母 线k可 观；adc，kj表 示 直流母线k和交流母线j之间的关联系数，按式（11）所示原则取值。

式（10）的物理意义为：当且仅当与直流母线k相应的换流母线j装配有量测装置时，直流母线k谐波状态可观。

2.1.3 交直流混联电网的完全可观性约束

联立式（8）和式（10），即可建立交直流混联电网的线性不等式可观性约束集：

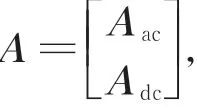
2.2 考虑成本和量测冗余度的bPMU 的Ⅰ阶段优化配置

2.2.1 量测成本指标

结合工程实际考虑，量测成本指标不仅计及bPMU 装置台数，还需考虑到不同数量的量测量造成的交流采集插件的插件成本差异。除了交流采集插件外，bPMU 装置的其余插件和模块均为固有配置。通常1 台bPMU 装置最多能配置5 个交流采集插件，且每个采集插件最多可量测12 个交流电气量，因此，需根据具体变电站所需量测交流电气量的数量，确定bPMU 装置的台数及其交流采集插件的插件数，以构成量测成本指标：

式 中：Fcost，1为 交 流 采 集 插 件 成 本；Fcost，2为 除 交 流 采集插件外的bPMU 固有成本；gi为母线i所在变电站配置bPMU 时所需要装配的交流采集插件数目，gi=ceil(3(Nu，i+Ni，i)/12)，其 中Nu，i为 母 线i所 在变电站的电压量测量数目，Ni，i为与母线i连接的支路数，即为变电站的电流量测量数目；ceil（·）表示向上取整函数。

2.2.2 量测冗余度指标

母线i量测冗余度定义为母线i可被观测的次数，可由yi表示：

量测冗余度指标除了计算交直流电网总冗余度，还需要考虑各个母线冗余度的均衡度。因此，综合交直流电网ngrid个母线的量测冗余度及其均衡程度构成电网的冗余度指标Jr：

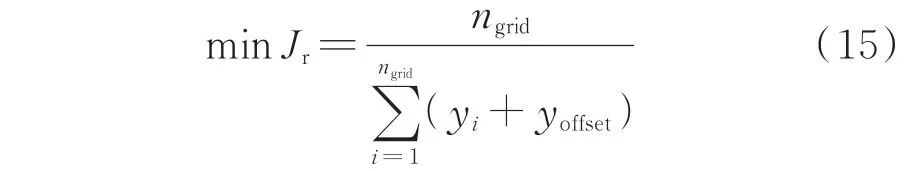
式中：yoffset表示母线i量测冗余度yi与量测冗余度平均 值yˉ的偏移程度，yoffset=-|/ygrid，其 中yˉ=为电网母线量测冗余度总和。电网母线量测冗余度总和越大，各母线量测冗余度越均衡，相应的冗余度指标Jr的分母部分就越大，因此量测配置方案的冗余度指标就越小。

2.2.3 Ⅰ阶段优化的目标函数

综合考虑量测成本指标和冗余度指标，Ⅰ阶段优化的目标函数为：

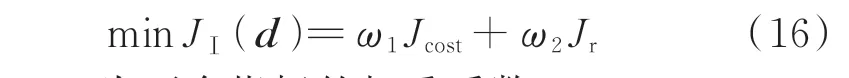
式中：ω1、ω2为两个指标的权重系数。

2.3 改进MPGA

Ⅰ阶段优化需要筛选出全局较优的nmax组解，以构成Ⅱ阶段优化的方案备选集。MPGA 具有全局搜索能力，但是只能输出唯一的最优解和部分全局较优解，为了使其能适用于Ⅰ阶段优化问题的求解，筛选出全局较优的nmax组解，本文提出了多输出的改进MPGA，主要改进以下方面。

1）精华种群更新机制

将历代所有种群中排列较前的nmax个精华个体记为精华种群Pmax，并在每次迭代后滚动更新Pmax，即第t次迭代时将本次迭代中所有种群的前nmax个个体的适应度值与Pmax，t-1的适应度值进行排序，取前nmax个精华 个体构成Pmax，t。

2）交叉概率pc和变异概率pm的自适应

在迭代初期，种群中多为适应度较低个体，pc、pm取值过小会导致不易产生新个体，迭代次数较多；在迭代后期，种群中多为适应度较高个体，pc、pm取值过大会导致优良个体被破坏，容易沦为随机搜索算法，而取值过小又会导致遗传个体多样性不足，不利于搜索全局较优解。因此，本文提出，随着迭代次数增多，逐渐增大pc和pm的下限；另外，还提出每个种群在每次迭代中基于个体适应度自适应调整个体pc和pm的方法，其自适应概率函数曲线如图4 所示，图中：pt，max、pt，min分别为某个种群第t次迭代的最大、最小交叉概率或变异概率；fmax、fmin分别为该种群第t次迭代的最大、最小个体适应度值。

第t次 迭 代 的 第m个 种 群Pm，t中，个 体n的 自 适应交叉概率pct，n的具体公式如下：

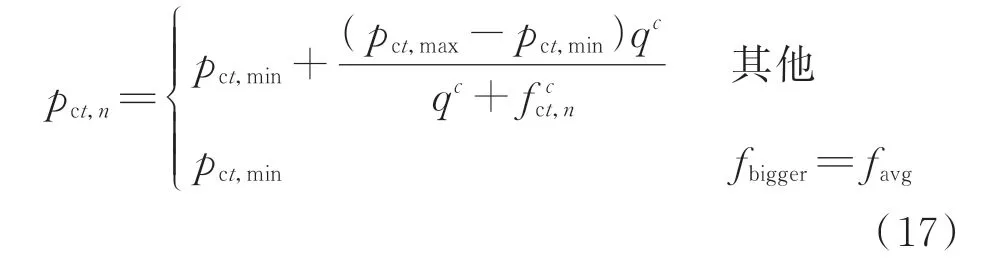
式 中：fct，n=(fbigger-fmin)/(fmax-fmin)，其 中fbigger为交叉运算中较大的个体适应度值；q、c用于调整图4所示自适应概率函数曲线，本文设q=0.75，c=7；favg为该种群第t次迭代的平均个体适应度值；pct，max、pct，min分别为该种群第t次迭代中的最大和最小交叉概率。

图4 自适应概率函数曲线Fig.4 Curve of adaptive probability function

迭 代 过 程 中，pct，max不 随 迭 代 次 数 改 变，而pct，min随着迭代次数线性增加，即：

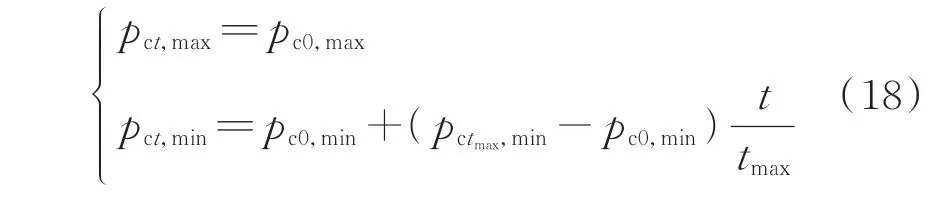
式 中：pc0，max、pc0，min分 别 为 该 种 群 最 大 和 最 小 交 叉 概率的初始设置值；pctmax，min为该种群最小交叉概率的最大设置值；tmax为最大迭代次数。

第t次 迭 代 的 第m个 种 群Pm，t中，个 体n的 自 适应变异概率pmt，n的具体公式如下：

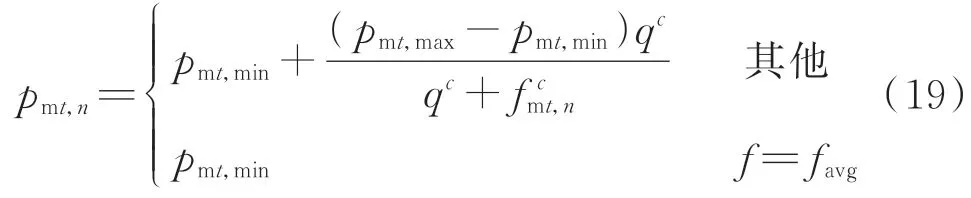
式 中：f为 个 体n的 适 应 度 值；fmt，n=(ffmin)/(fmax-fmin)；pmt，max、pmt，min分 别 为 该 种 群 第t次迭代中最大和最小变异概率，其变化趋势和交叉概率相似，如式（20）所示。

式中：pm0，max、pm0，min分别为该种群最大变异概率、最小变异概率的初始设置值；pmtmax，min为该种群最小变异概率的最大设置值。

3）移民运算

将 第m个 种 群Pm，t的 最 劣 解 由 第m-1 个 种 群Pm-1，t的较优解代替，保证全局搜索的可靠性和个体的遗传多样性。

综上，改进MPGA 的具体运算步骤如图5 所示，其中T为最优个体保持不变的代数，Tmax为最优个体保持不变的最大代数。

图5 改进MPGA 流程图Fig.5 Flow chart of improved MPGA

2.4 增加考虑鲁棒性的bPMU 的Ⅱ阶段优化配置

基于Ⅰ阶段优化筛选出的备选方案集，在Ⅱ阶段优化综合考虑成本指标、冗余度指标和鲁棒性指标，确定一组最优bPMU 配置方案。

交直流混联电网统一谐波状态估计模型的鲁棒性与量测矩阵H的病态程度有关，可由条件数K(H)=σmax/σmin表征，其中σmax、σmin分别为矩阵最大、最小奇异值。基于量测优化配置的可观性约束可知，LCC 相应的换流母线必定安装bPMU，所以在不同的量测配置方案中，线性统一谐波状态估计模型式（7）的Hdc，ac、Hdc，dc是相同的，不同之处在于Hac中的各次交流谐波量测矩阵。因此，鲁棒性指标为：

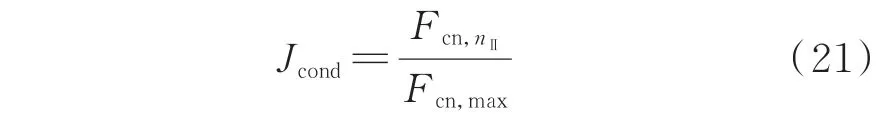
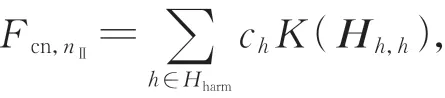
增加考虑式（21）鲁棒性的指标，Ⅱ阶段优化的目标函数为：

3 算例分析

为了验证本文所提的交直流混联电网统一谐波状态估计方法、bPMU 综合优化配置模型及其分阶段求解方法的正确性和有效性，本文基于PSCAD/EMTDC 构建了附录A 图A1 所示的仿真算例。该电网包含两个220 kV 交流电网，分别包含14 条和12 条交流母线，并通过“两交两直”线路将它们连接，其中直流线路为CIGRE-HVDC 系统标准模型，LCC 均为十二脉动换流器，具体线路及变压器参数见附录A 表A1、表A2。仿真及运算所用的计算机配 置 为Windows 10（64 bit），8.00 GB 内 存，Intel Core i5-8400 CPU。

3.1 bPMU 综合优化配置建模及分阶段求解方法

针对附录A 图A1 所示算例，利用MATLAB 编写bPMU 综合优化配置建模及分阶段求解方法的程序。首先，建立考虑成本和量测冗余度的bPMU的Ⅰ阶段优化配置模型，基于改进MPGA 获得50 种备选配置方案；然后，根据增加考虑鲁棒性的Ⅱ阶段优化目标函数进行排序，如表1 所示，表中仅列出Ⅱ阶段优化目标函数较小的前6 种备选方案。其中，利用层次分析法（analytic hierarchy process，AHP）给 出 Ⅰ 、Ⅱ 阶 段 优 化 目 标 函 数JⅠ(d)、JⅡ(d，H)中不同指标的权重：ω1=0.875 0、ω2=0.125 0；=0.778 8、=0.111 1、=0.111 1。另外，考虑到12h±1 次谐波的幅值相近，且随着h增大，谐波的幅值逐渐减小、传播过程中衰减更快、重要性降低，因此，根据谐波幅值大小，利用AHP 给鲁棒性指标中不同次数的谐波量测矩阵Hh，h的条件数赋予权重，重点考虑50 次以下的条件数K(Hh，h)，各次谐波量测矩阵的条件数 权 重 为：c11=c13=0.329 3，c23=c25=0.108 1，c35=c37=0.041 0，c47=c49=0.021 6。

表1 交直流混联电网的备选量测配置方案Table 1 Alternative measurement configuration schemes for AC/DC hybrid power grid

6 种备选方案具体的各项指标如表2 所示，方案A 不仅保证了电网的完全可观性和低成本性，而且有利于提高谐波状态估计的精确性，因此可确定方案A 为最优方案。

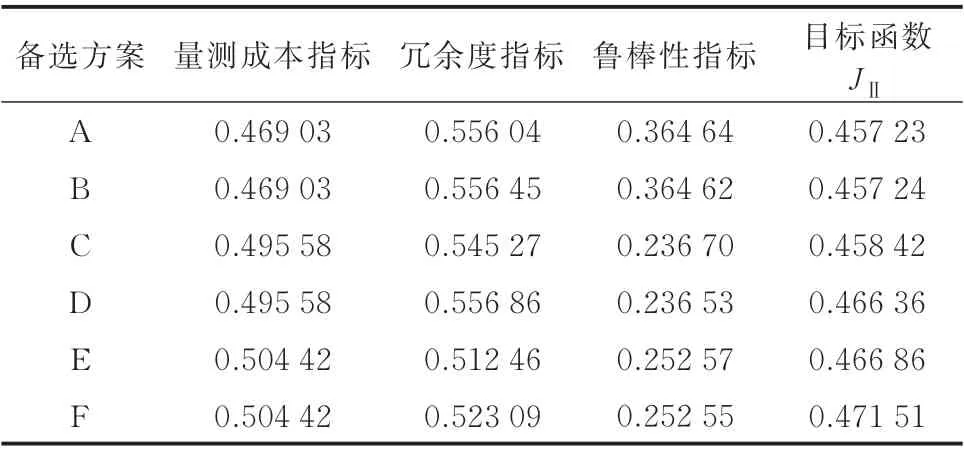
表2 备选量测配置方案的各项指标Table 2 Indicators of alternative measurement configuration schemes

另外，将本文方法与基于MPGA 的分阶段优化方法、基于MPGA 的不分阶段优化方法进行比较，结果如表3 所示，可见本文方法收敛到全局最优的效果最好，运算速度快。

表3 算法对比结果Table 3 Comparison result of algorithms

3.2 统一谐波状态估计

基于bPMU 最优配置方案A，利用MATLAB编写交直流混联电网统一谐波状态估计程序。同时，向量测数据中各次谐波的幅值加入±0.5%的正态分布误差，相位加入±0.4°的正态分布误差，且随机选取部分数据加入10%～50%的幅值误差和2°～15°的相角误差，采用基于IGGⅢ权函数抗差最小二乘法进行求解。

所得估计值与仿真值的误差结果如图6 所示，图中分别给出了各LCC 直流母线和各交流母线谐波电压估计值的幅值相对误差和相位绝对误差。由图6 可知，谐波电压幅值最大个体相对误差低于5%，谐波电压相位最大个体绝对误差低于5°。其中，部分母线谐波电压误差结果明显高于其他母线，是因为其幅值相对较小，较小的仿真误差或者估计误差也会造成较大的误差（各母线谐波电压的幅值及相位见附录A 表A3—表A6），但是总体上误差满足工程要求。同时可见，本文所提的统一谐波状态估计模型不同于现有谐波状态估计模型，不仅能获得交流电网谐波状态，而且在物理概念上能清晰地反映交直流系统间谐波相互作用，从而能同时准确地估计直流电网的谐波状态，这是现有谐波状态估计方法无法做到的；本文基于IGGⅢ权函数抗差最小二乘法的统一谐波状态估计，具有较好的抗差能力，可在含量测误差的情况下较为准确地估计含LCC-HVDC 的交直流混联电网的谐波状态。

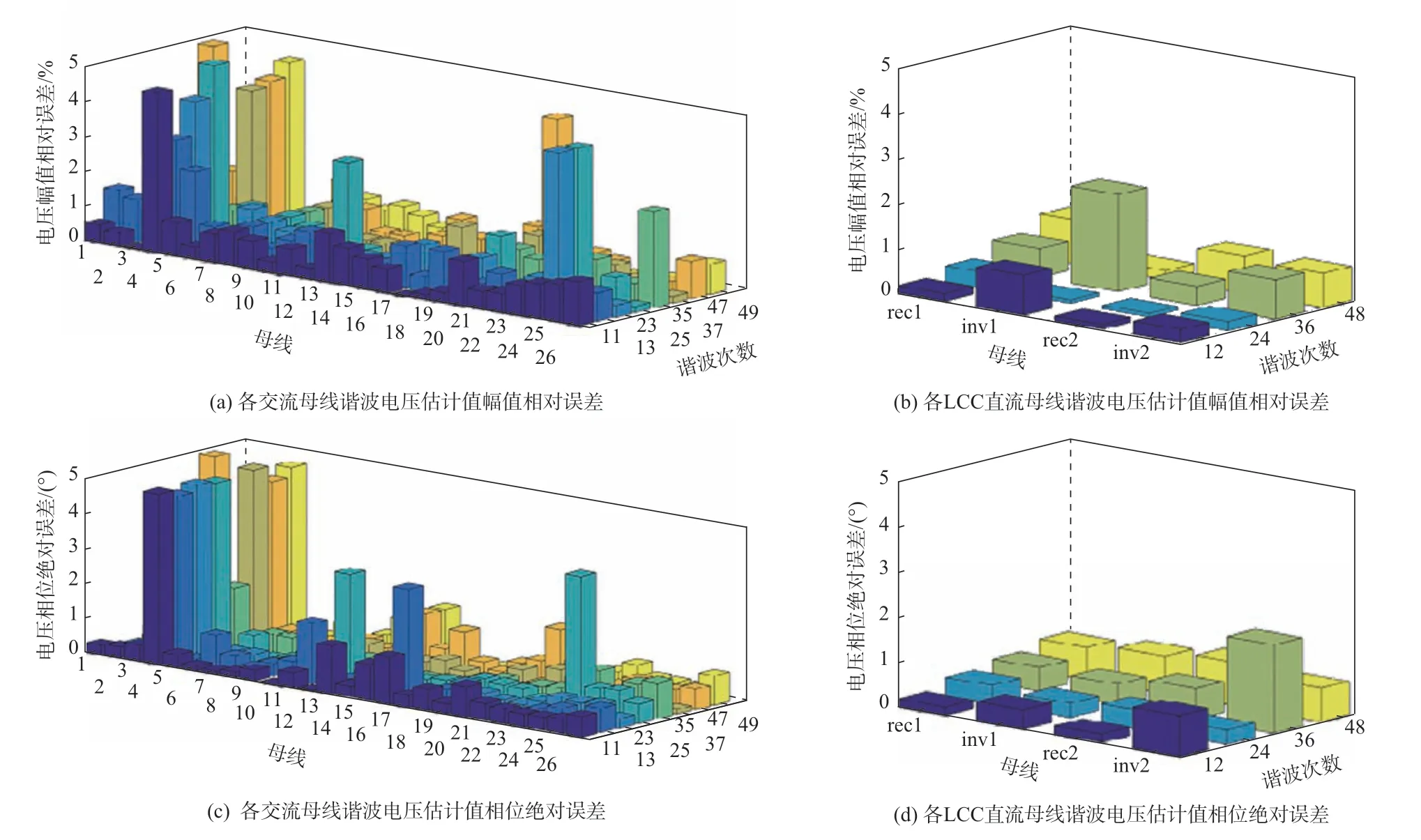
图6 统一谐波状态估计误差分析Fig.6 Error analysis of unified harmonic state estimation

4 结语

本文针对含LCC-HVDC 的交直流混联电网谐波分析问题，基于动态相量法建立了交直流系统间谐波传递模型，提出了统一谐波状态估计方法、bPMU 综合优化配置模型及其分阶段求解方法，得到如下结论：

1）交直流混联电网统一谐波状态估计模型不仅能从调制机理上明晰交直流系统间的谐波相互作用，实现交直流混联电网的统一谐波状态估计，且运算速度和计算精度能够满足工程应用需求；

2）本文提出的bPMU 综合优化配置模型及其分阶段求解方法能够在保证交直流混联电网的完全可观性的前提下，优化广域宽频同步监测系统成本，提升谐波状态估计的精度和鲁棒性，与传统方法相比收敛效果更好，具有良好的工程实用性。

由于实验条件的限制，本文仅基于PSCAD/EMTDC 对所提统一谐波状态估计方法进行了数字仿真验证，未能在半实物仿真平台上验证，且课题组研制的bPMU 尚未投入电网，因此也无法得到工程验证。交直流混联电网的统一动态谐波状态估计将是下一步的研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。