适用于配电网三相优化潮流的数据物理融合驱动线性化方法

巨云涛，杨明友，吴文传

（1. 中国农业大学信息与电气工程学院，北京市 100083；2. 清华大学电机工程与应用电子技术系，北京市 100086）

0 引言

潮流方程的非线性给配电网的优化调控带来了挑战，如非线性交流最优潮流的收敛性和全局最优无法保证［1-3］，随着配电系统规模变大，计算效率也会变低［4-5］。采用线性潮流模型代替原有非线性潮流方程，可降低配电网优化模型的求解难度，保障算法的收敛性，提高计算效率［6-7］。而潮流模型线性化精度决定了线性化最优潮流的适用性。

直流潮流模型是目前输电网中应用最多的线性模型［8］，但由于配电网电阻/电抗比高，直流潮流模型应用于配电网分析时会产生较大误差［9-10］。此外，目前提出的线性潮流模型多为假设三相完全对称的单相线性潮流模型［11-16］，这些线性化方法并不适用于三相不平衡特征明显的配电网［17-18］。因此，国内外学者提出了适用于三相不平衡配电网的线性潮流模型。文献［19-20］提出基于泰勒一阶展开的三相线性潮流模型；文献［21-22］提出适用于三相不平衡配电系统优化问题的Lin3DistFlow 线性潮流模型。这些三相潮流线性化方法在系统轻载时的计算精度在可接受范围内，但是在重载时线性化误差往往很大，这也是目前很多线性化方法需要解决的关键问题。

为了提高线性化潮流模型精度，可采用数据驱动类方法，该类方法通过对潮流数据的回归分析得到自变量和状态变量之间的线性关系［23-24］。虽然数据驱动线性化方法在大多数测试算例中的精度高于物理模型驱动的线性化方法，但是该方法无法保留线路连接关系信息，不易在优化潮流中描述支路约束。

针对以上问题，学者提出了数据物理融合驱动的线性化方法［25-27］。文献［25］提出基于数据物理融合驱动的支路潮流模型，其精度较文献［11-16］中模型的精度有很大提升，但其为单相线性潮流模型，不适用于三相不平衡特征明显的配电网。文献［26］采用最小二乘法获得误差修正项来提高线性化精度，但其无法考虑分布式电源（distributed generator，DG）以及三角形恒功率负荷模型。文献［27］基于经典电流注入法，通过最小二乘法拟合节点等效注入电流与负荷的线性关系，最终得到数据物理融合驱动的三相线性潮流模型，与文献［19-20，22］中的线性化方法相比，其精度有了明显提升，但在系统运行状态为重载时的精度仍然较低。

综上所述，本文结合数据驱动和物理模型驱动2 种线性化方法，提出了一种适用于配电网三相优化潮流的数据物理融合驱动线性化方法。主要贡献如下：

1）综合了物理模型驱动方法和数据驱动方法的优点，既通过物理模型驱动方法保留了线路的连接关系，又可以充分利用数据驱动的优化拟合能力获得线性化误差模型。通过偏最小二乘（partial least squares，PLS）回归将误差转换为高维状态空间的线性映射，以系统中所有的三相负荷为状态变量来描述线性化误差，并将线性化误差模型加入线性潮流模型，保证重载时所提方法的精度仍然足够高。

2）所提线性化方法具有更好的适用性，考虑了各种连接方式的三相变压器和负荷模型以及相间耦合的DG 三相模型。

3）在使用PLS 回归时，只需使用较少的训练样本便可获得误差与负荷的线性关系，且能保证最终的线性化精度在可接受范围内。

1 基于物理特性得到的线性潮流模型

1.1 线性化原理

为了得到物理模型驱动的线性潮流方程，根据实际配电网情况给出线性近似的基本原理：

1）系统运行时，各节点电压均在基准值附近，所以电压幅值约为1.0 p.u.；

2）在极坐标形式的潮流方程中存在节点相角的正弦和余弦非线性项，参考文献［19］中的网络模型，可将其近似处理，如式（1）和式（2）所示。

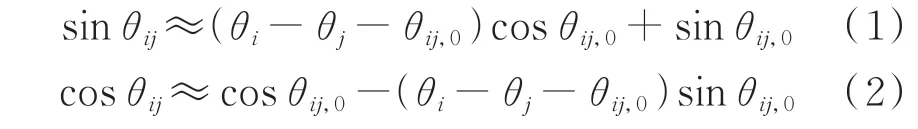
式中：θi和θj分别为节点i和j的电压相角；θij=θiθj为相角差；θij，0为初始相角差且θi-θj-θij，0≈0。

配电网三相线性潮流模型包括线路模型、变压器模型、负荷模型和DG 模型，这里详细介绍后3 种模型，线路模型详见附录A。

1.2 三相变压器的线性化模型

三相变压器模型包含星形/星形、星形/三角形、三角形/星形和三角形/三角形4 种连接方式［28］。虽然变压器的连接方式不同，但无论何种型号的三相变压器均可以由节点导纳矩阵表示，变压器节点导纳矩阵求解过程详见附录B。如附录B 图B2 所示，三相变压器共有6 个节点和6 条支路。为防止零漂问题，需要在变压器未接地侧接入接地大阻抗Rmax，本文设其值为1×109Ω。变压器6 个节点的等效节点注入功率可表示为：

式中：Ui和Uj分别为节点i和j的电压幅值；Pi和Qi分别为三相变压器节点i的注入有功功率和无功功率；Gij和Bij分别为变压器节点导纳矩阵（6×6 的复数矩阵）第i行、第j列元素的实部与虚部；ki表示变压器端子i是否接地，ki=0 表示接地，ki=1 表示不接地。

式（3）中 存 在 非 线 性 项UiUjcosθij和UiUjsinθij，根据1.1 节给定的线性近似原理可得：

所以变压器节点注入功率的线性表达式为：

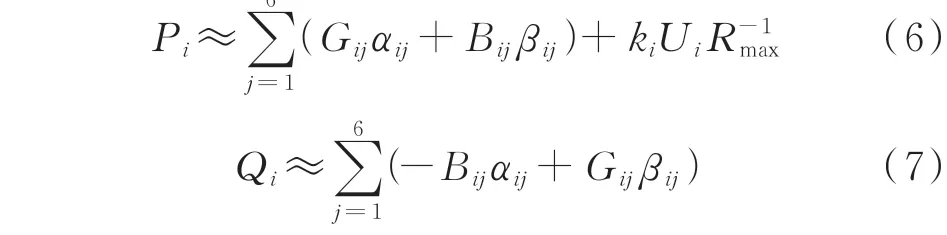
1.3 三角形恒功率负荷线性化模型

电动机是中低压配电网中常见的三角形恒功率负荷。为了在优化潮流中考虑三角形恒功率负荷，本文根据图1 所示模型给出了其线性潮流方程。

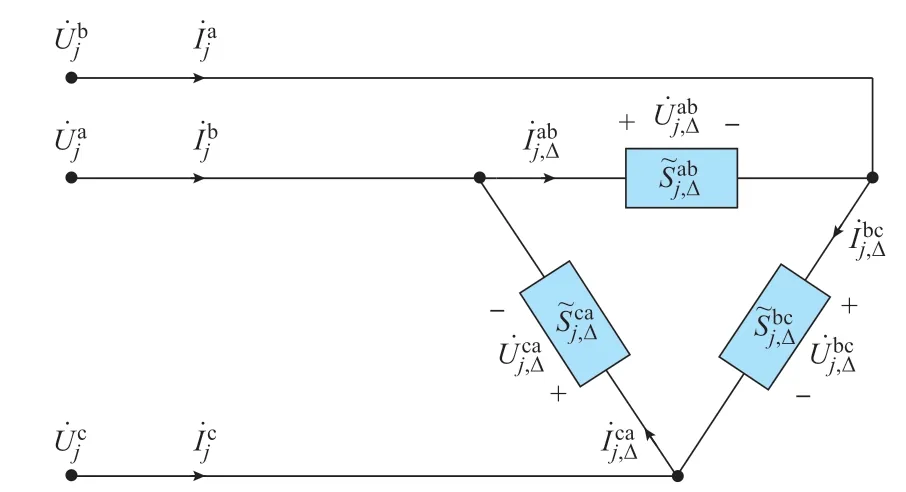
图1 三角形恒功率负荷模型Fig.1 Model of triangular constant power load

三角形恒功率负荷的负荷电流为：

由此可以得到三角形恒功率负荷节点等效注入功率的线性方程为：

式中：系数α=(1/2)-j 3 /6，β=(1/2)+j 3 /6。

1.4 DG 线性化模型

本文采用文献［28］描述的DG 模型，DG 满足结构参数对称的特点，采用序分量描述更方便。具体建模详见附录B，下面给出DG 的线性潮流约束。

1.4.1 零序分量

由于DG 采用三角形变压器隔离零序电流，所以零序电流为零，则DG 的零序电流方程如式（14）和式（15）所示。设共有s个节点与DG 相连，则DG节点导纳矩阵是一个3×3(s+1)的复数矩阵。公式推导详见附录C 第C1 章。

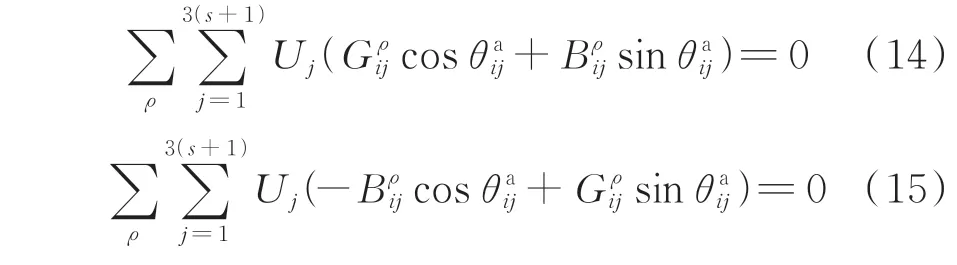
式中：ρ取a、b、c，表示a、b、c 相；和分别为DG节点导纳矩阵第i行、第j列元素的实部与虚部；=-θj为DG 所连 母 线i的a 相 相 角与θj的相角差。

1.4.2 负序分量

如果DG 不增加负序电流控制，负序电压和电流的关系呈负荷阻抗特性，可表示为阻抗方程。DG负序电流约束及线性化公式的推导详见附录C 第C2 章，最终得到的DG 负序电流约束线性表达式为：

观察两组患者的治疗效果，观察两组患者的护理满意度及生活质量。生活质量采用SF-36量表评分，得分越高，生活质量越高。

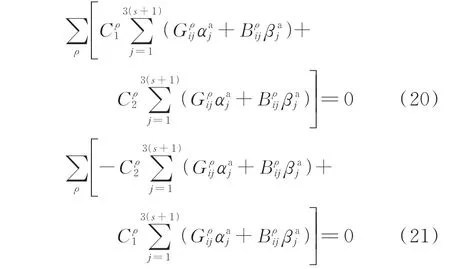
1.4.3 三相总加功率

配电网中DG 在优化潮流中的三相总加有功和无功功率都可控，总加功率方程如式（22）、式（23）所示，详细的公式推导见附录C 第C3 章。

1.5 线性化模型

基于配电网物理特性得到的线性潮流方程可表示为：

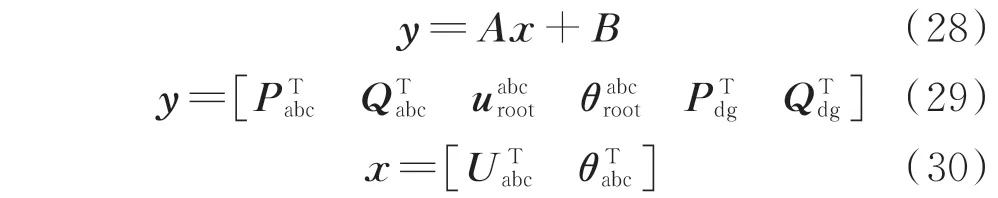
式中：y为已知量，即最优潮流问题中的变量；x为状态变量；Pabc和Qabc分别为三相有功和无功功率向量；和分别为平衡节点的三相电压幅值和相角向量；Pdg和Qdg分别为DG 总加有功和无功功率向量；Uabc和θabc分别为三相电压幅值和相角列向量；A和B分别为线性潮流方程的系数矩阵和常系数矩阵。

1.6 线性化方法适用性的讨论

在常用的线性化模型中，文献［13］通过复平面内的电压线性近似得到可以处理ZIP 负荷的线性潮流模型；文献［14］利用电压幅值的对数变换，通过对支路潮流的近似分析得到包含分接头和移相器的线性潮流模型；文献［19］中提出的极坐标系下的线性潮流模型可以处理星形和三角形连接的ZIP 负荷以及三相DG 等模型；文献［29］通过泰勒一阶展开得到可以处理各种类型DG 的线性潮流模型。但以上线性模型中均存在功率乘电压项，不适用于功率为变量的优化潮流建模。文献［30］采用基于库普曼算法的升维思想，通过提升维度来提高线性化模型的精度，但如果节点功率为待求变量，则潮流约束为非线性函数，故无法适用于优化潮流问题。

在已知的适用于优化潮流的线性化方法中，文献［20］提出的线性化模型虽然可以处理三角形连接的恒功率负荷模型，但未考虑DG 模型，适用性不足；文献［22］中的Lin3DistFlow 线性潮流模型无法处理DG 和三相变压器模型；文献［26］提出的线性化方法未考虑到DG 模型；文献［27］中的线性化方法无法处理三角形连接的恒功率负荷和DG 模型。

相比于其他线性化方法，本文基于配电网物理特性得到的线性化模型完全适用于优化潮流问题，且对三相不平衡系统有更好的适用性，可以处理各种连接方式的变压器和负荷以及DG 三相模型。

2 数据驱动

当系统的运行状态为重载时，电压幅值远离参考电压（1.0 p.u.），此时基于配电网物理特性得到的线性潮流方程在用于优化潮流时会产生较大的误差。因此，本文通过在线性潮流模型中加入线性化误差来修正线性潮流方程，从而提高计算精度。而潮流方程的误差同样具有高度的非线性特征，本文通过PLS 回归的数据驱动方法获得线性化误差Δy的模型。

式中：C和D分别为通过PLS 回归得到的系数矩阵和常系数矩阵；ΔPabc和ΔQabc分别为三相有功和无功功率的线性化误差向量；ΔPdg和ΔQdg分别为DG有功和无功功率的线性化误差向量；y′为系统中的三相负荷列向量；和分别为非零三相有功和无功功率列向量。

2.1 数据的获取

本文设定训练数据和测试数据可以通过2 种方法获得。

1）交流潮流模型

当系统线路参数已知时，可以基于交流潮流模型生成训练数据集和测试数据集。设系统的初始有功和无功负荷向量为和，共需要生成m组样本数据，则系统三相负荷可按照如下方式随机生成：

2）从量测数据获得

随着高级量测体系（AMI）的部署和微同步相量测量单元（MicroPMU）等量测设施的应用，可以从历史测量数据中获得足够的数据用于PLS 回归。

2.2 自变量集和因变量集的生成

设共有m组样本数据，其中包含节点负荷、三相电压幅值和相角，上标“^”表示已知量。第m组节点负荷构成自变量集R，即R=[]。将样本数据代入线性潮流方程求解 可 得 到 因 变 量 集Z=[]，其 中为求得的第m组误差修正项。

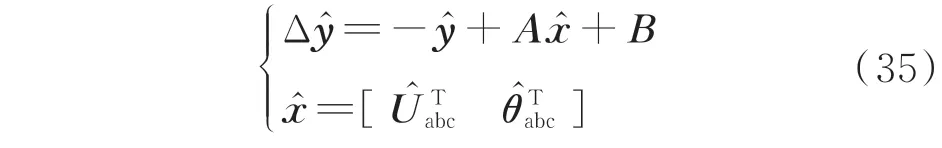
2.3 回归系数的求解

在PLS 回归中，为输入变量和预测变量提取彼此之间协方差最大的正交列向量对集。这些向量进一步用于获得输入变量和预测变量之间的线性关系。

在得到自变量集和因变量集后，将数据集标准化后可得：

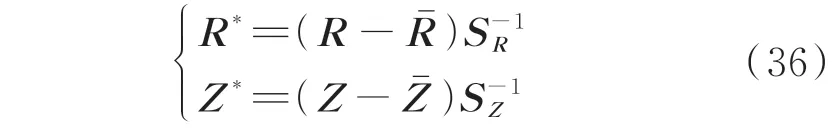
式中：R*和Z*分别为标准化后的自变量集和因变量集；和SR分别为自变量集R的均值和标准差；和SZ分别为因变量集Z的均值和标准差。

式中：β为通过PLS 回归求得的回归系数矩阵。

最终的数据物理融合驱动的线性潮流方程为：

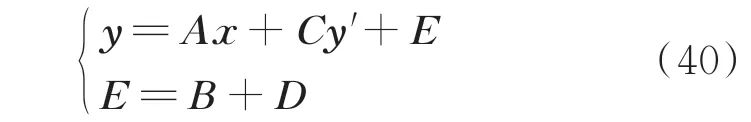
2.4 误差的线性化模型精度

误差的线性化模型精度决定了数据物理融合驱动线性化模型的精度。文献［30-31］证明可通过提升维度来提高线性化模型的精度。本文所采用的线性化误差模型中，状态变量为系统中的非零负荷列向量，每个误差均由所有非零负荷线性表达，即采用更多维信息描述误差，可显著提高线性化误差模型的精度。随着系统规模扩大、系统中的负荷增多、线性化误差模型的维数增大，线性化误差模型的精度也会增大。为了说明误差线性化模型的维度对整体线性化模型精度的影响，设计了一个三相不平衡的3 节点辐射状系统，该系统参数见附录D 第D1 章。系统的拓扑结构见附录D 图D1。图中，节点1 为平衡节点，电压幅值恒为1 p.u.，节点2 处bc 两相和节点3 接有负荷。

设有30 组训练样本，各节点误差的线性表达式为：

图2 的结果表明，随着维度的提升，线性化模型的精度也逐渐提高。

图2 线性化精度与维度的关系Fig.2 Relationship between linearization precision and dimension

3 算例分析

3.1 基准模型

本文通过测试以下5 种线性化模型进行精度比较。

M1：本文提出的数据物理融合驱动的线性潮流模型。

M2：本文第1 章中给出的基于配电网物理特性得到的三相线性潮流模型。

M3：文献［20］中提出的适用于配电系统强化学习训练的线性潮流模型，该方法以电压幅值的对数函数和相角作为状态变量。

M4：文献［27］中提出的基于经典电流注入法的数据物理融合驱动三相线性潮流模型，以电压实、虚部作为状态变量。

M5：文献［22］中提出的适用于三相不平衡系统的Lin3DistFlow 线性化潮流模型，以电压幅值的平方和支路功率作为状态变量。

3.2 评估框架

通过所有测试算例中的支路功率和节点电压幅值的AAE 和MAE 比较线性化模型的精度。其中，AAE 的表达式为：

式中：N为所有测试算例中的变量数；yn为第n个变量的真实值；为用线性潮流模型计算得到的第n个变量的线性值。

3.3 精度对比

选用IEEE 13 节点、34 节点、37 节点和123 节点系统进行算例测试，算例的训练数据样本数分别设置为100、200、200 和600 组［19］，4 个算例均设置为重载。训练数据和测试数据中的负荷在初始负荷的90%～110%内随机变化。所有算例的测试数据均设为900 组。最终求得4 个测试系统的电压幅值、支路功率的AAE 和MAE 分别如表1 和表2 所示。

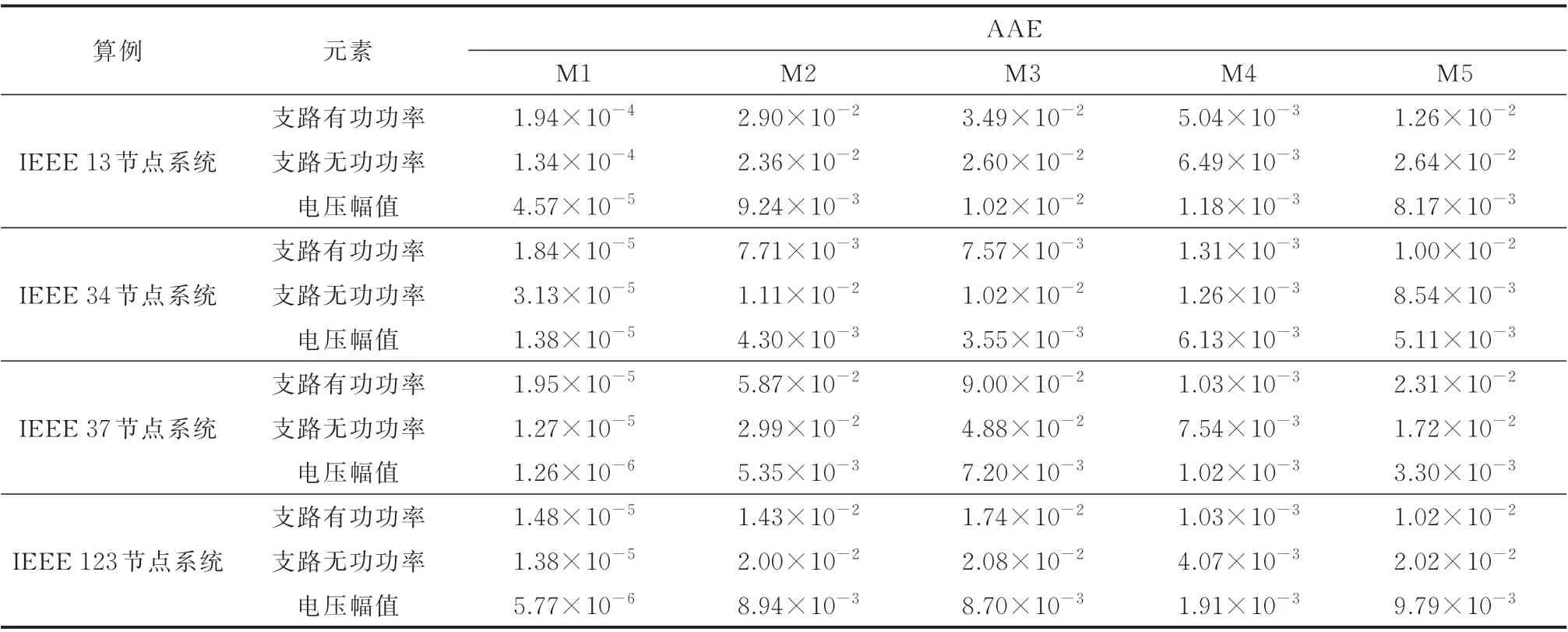
表1 AAE 对比Table 1 Comparison of AAEs

表2 MAE 对比Table 2 Comparison of MAEs

由表1 和表2 可知，所提三相潮流线性化方法的AAE 和MAE 至少比其他4 种线性化方法的结果低一个数量级。

3.4 模型在大规模系统中的效果验证

当系统规模更大时，分析所提线性潮流模型的适用性。选用改进的IEEE 8 500 节点系统进行测试，PLS 回归训练数据生成方式与上述IEEE 13 节点系统相同。由于系统规模更大，为了保证计算结果的精度，采用3 000 组训练数据用于PLS 回归拟合求误差修正项。将系统的运行状态设置为轻载和重载2 种状态，重载即对应系统的极端运行条件，部分节点的电压幅值降至0.75 p.u.附近，因为电压幅值远离参考电压（1.0 p.u.），此时交流潮流模型具有高度非线性特征，所以物理模型驱动的线性潮流方程具有较大误差。误差对比和分布分别如表3 和图3 所示。

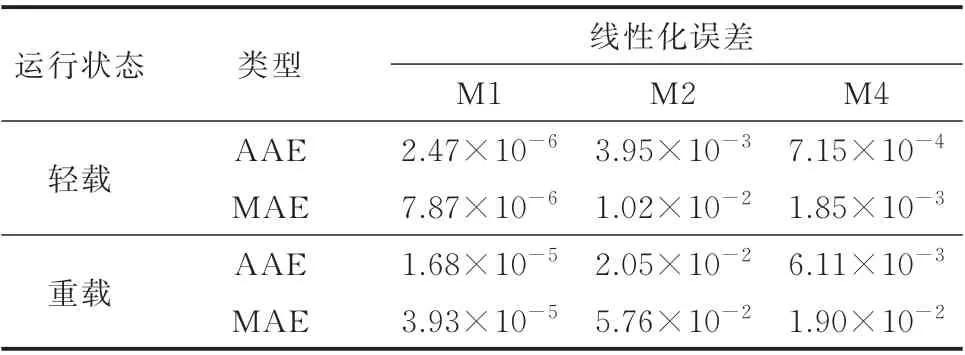
表3 IEEE 8 500 节点系统线性化误差对比Table 3 Comparison of linearization errors in IEEE 8 500-bus system

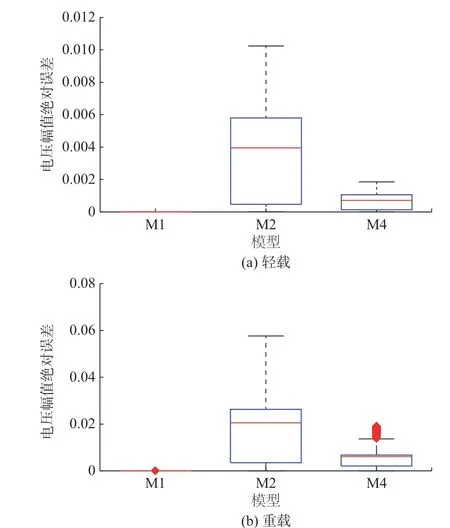
图3 IEEE 8 500 节点系统三相电压幅值线性化误差分布Fig.3 Linearization error distribution of three-phase voltage amplitude in IEEE 8 500-bus system

表3 和图3 的结果表明，在轻载和重载2 种运行状态下，所提线性化方法电压幅值的AAE 和MAE相较于线性化模型M2 和M4 的结果，至少低2 个数量级。在系统重载时，所提线性化方法的电压幅值的MAE 仅为3.93×10-5，比线性化方法M2 和M4的结果低3 个数量级，这表明所提线性化方法适用于运行状态为重载时的大规模系统优化潮流。

3.5 模型适用性分析

选用改进的IEEE 13 节点系统进行模型适用性分析，其系统拓扑如附录D 图D2 所示。节点13 处的负荷类型为三角形恒功率负荷；节点12 处加入DG；节点5 和节点6 之间加入一台DYn11 变压器，以变压器两侧的相电压为电压基准值，可得变压器的标幺值变比为 3 ∶1，其标幺值变比求解过程详见附录D 第D2 章。由于M3 至M5 均无法考虑DG，本文仅与M2 进行精度对比。2 种线性化方法的电压幅值绝对误差如图4 所示。

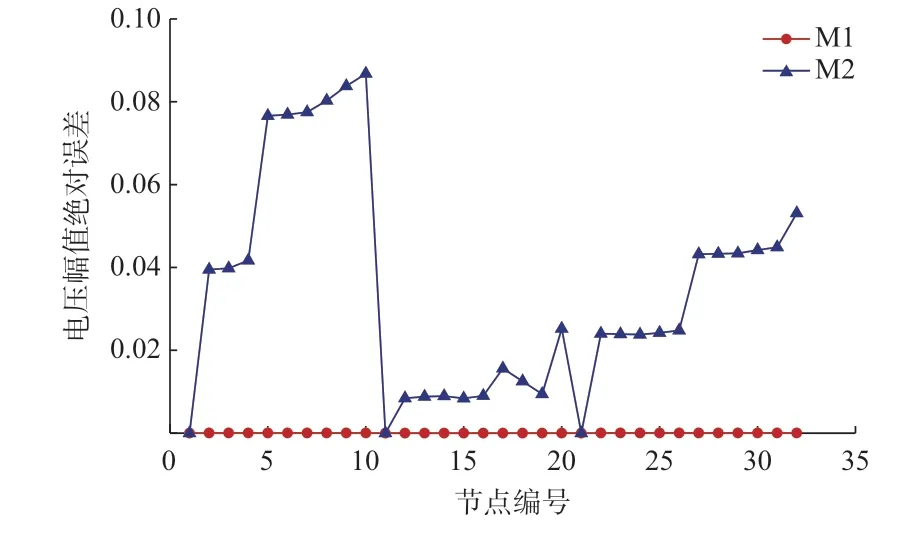
图4 改进的IEEE 13 节点系统电压幅值绝对误差Fig.4 Absolute errors of voltage amplitude in improved IEEE 13-bus system

图4 的结果表明，所提线性化方法的精度远远高于线性化模型M2，所提方法的MAE 仅为2.91×10-5，AAE 比M2 的 结 果 低3 个 数 量 级。这 表 明 所提线性化模型适用于含变压器、DG 和三角形恒功率负荷的系统，具有很强的适用性。

3.6 训练数据对线性化精度的影响

为了测试训练数据和测试数据中负荷随机变化范围对数据物理融合驱动线性化方案精度的影响，以IEEE 13 节点系统为例，在以下3 种场景下生成三相随机负荷。

场景1：负荷随机变化范围为初始负荷的90%～100%。

场景2：负荷随机变化范围为初始负荷的85%～115%。

场景3：负荷随机变化范围为初始负荷的80%～120%。

根据2.1 节中的方法获得所需的训练数据和测试数据，得到3 种场景下IEEE 13 节点系统的误差分布如图5 所示。结果表明，随着拟合数据中负荷变化范围的扩大，所提线性化方法的精度会降低，这是因为随着负荷变化范围的增大，误差修正项与各节点负荷之间的相关性降低。

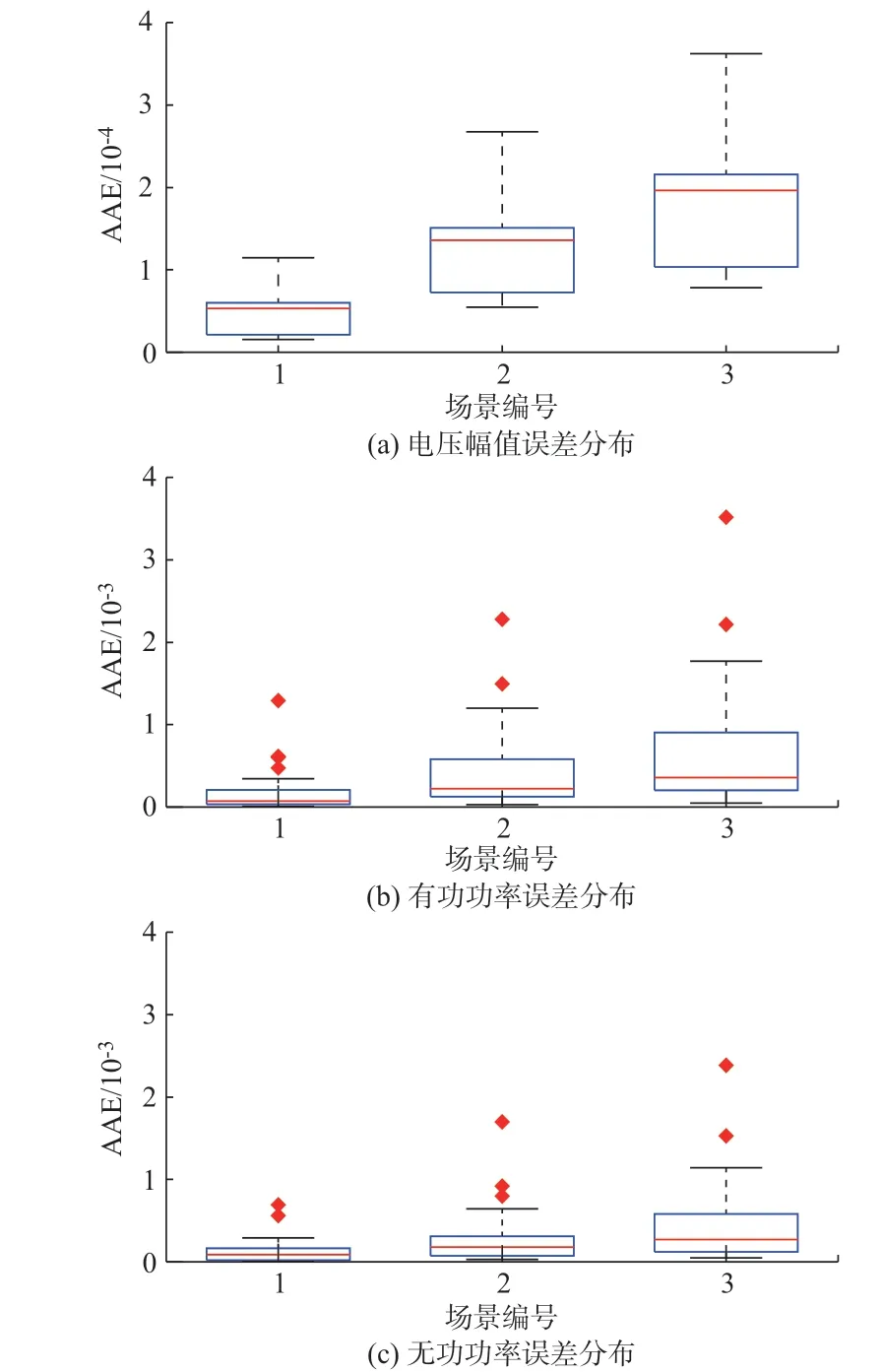
图5 IEEE 13 节点系统线性化误差分布Fig.5 Linearization error distribution of IEEE 13-bus system

进一步将负荷随机变化范围设置在初始负荷的70%～130%之间随机变化，采用IEEE 13 节点系统测试，训练数据仍设置为100 组，最终得到本文所提线性化方法与线性化模型M4 的电压幅值误差对比如图6 所示。结果表明，当拟合数据中负荷变化范围较大时，所提线性化方法的精度仍然高于M4，而M4 是除所提方法以外精度最高的一种线性化方法。

图6 IEEE 13 节点系统电压幅值绝对误差Fig.6 Absolute error of voltage amplitude in IEEE 13-bus system

3.7 训练数据样本数对线性化精度的影响

本文所提线性化方法在利用PLS 回归获取误差的线性化模型时，只需要少量的训练数据样本即可获得精度较高的结果。选用IEEE 13 节点、IEEE 34 节点、IEEE 37 节 点、IEEE 123 节 点 和IEEE 8 500 节点算例进行测试，负荷变化范围设置与3.3 节相同，只用少量训练数据样本拟合求误差的线性化模型，设系统可接受的最大AAE 为5×10-4，最大MAE为1×10-3，最终得到各算例线性化精度和训练数据样本数的关系如表4 所示。

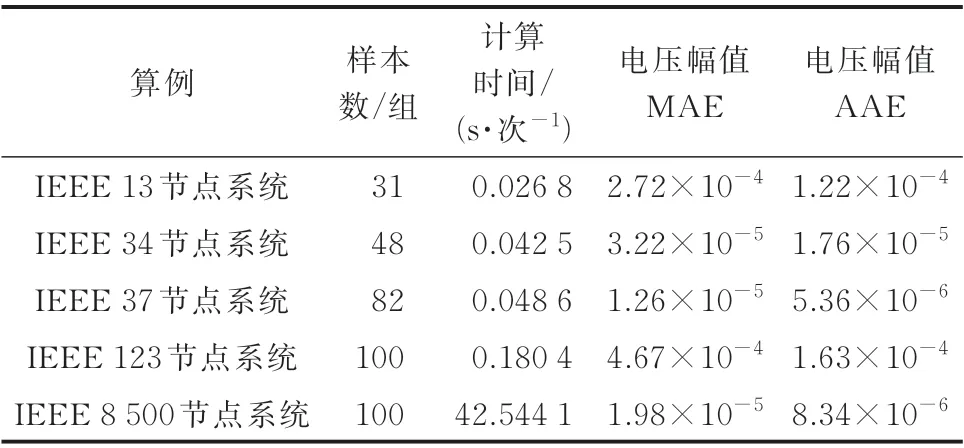
表4 各算例PLS 回归所需的最小样本数Table 4 The minimum number of samples required for PLS regression in each case

表4 结果表明，本文的线性化方法可以用较少的训练数据样本获得精度足够的线性化误差模型。

4 结语

本文提出了一种适用于配电系统优化问题的数据物理融合驱动型的线性化方法。使用PLS 回归拟合得到误差与节点负荷的线性关系，再将求得的线性化误差模型加入基于配电网物理特性得到的线性潮流模型，最终得到数据物理融合驱动的线性潮流模型。

算例结果表明，所提线性化方法精度远远高于其他线性潮流模型，在系统运行状态为重载时也能保持较高的求解精度，并且能够应用于含变压器、三角形恒功率负荷和DG 的配电网优化潮流问题。

后续还将对该线性化模型在交直流混联系统优化调度、中低压配电网规划等领域的应用进行进一步的研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。