润滑作用下平面正弦钢球传动机构法向接触刚度研究
李美求,陶文杰,郑瑞波,宁林飞,华剑
1.长江大学机械结构强度与振动研究所,湖北 荆州 434023 2.中国石化江汉油田分公司江汉采油厂,湖北 潜江 433123
平面正弦钢球传动机构是一种轻量化的活齿结构,不仅丰富了传动机构的种类多样性,而且还符合油气装备智能化工业领域的发展需求,尤其是在油气开采井下作业过程中,由于井眼空间限制,小型轻量化的活齿传动结构具有良好的应用前景。因此,关于平面正弦钢球传动机构的机械性能需要提出更高的设计标准,以提高材料机械性能的稳定性[1,2]。其中,活齿与其他机构元件之间的接触特性是评价机构承载能力和使用寿命的重要标准。如果钢球-轨道接触面的接触刚度过小,那么机构承受载荷的传动元件将产生不可逆转的塑性变形和接触疲劳损伤。并且,通常情况下钢球-轨道接触面都处于润滑状态。因此对接触面在润滑条件下的接触刚度进行研究,归纳总结出接触面微观形貌和材料性能参数对接触面接触刚度的影响规律具有重要的理论和实际应用意义。
长期以来,国内外许多研究学者对粗糙接触面的接触特性都进行了大量研究[3,4],其中以Majumdar和Bhushan提出的M-B分形理论最具有代表性,但是M-B分形理论忽略了弹塑性临界变形状态[5]。随后,温椒花等[6]、王南山等[7]研究人员又建立了一个包含弹性、弹塑性变形、塑性变形3种变形状态的分形力学模型;孙见君等[8]建立了接触面之间与测量尺寸无关的力学分形模型;CHEN等[9]进行了考虑摩擦应力因素的球面结合面法向接触刚度分形模型基础研究。
以上接触模型并没有考虑润滑作用,实际上,大部分传动机构元件之间的接触面靠润滑介质来降低磨损[10]。因此很多学者开始研究在润滑作用下的接触刚度,肖会芳等[11]提出了混合润滑状态下粗糙接触面的法向刚度模型;GASNI等[12]以超声波的方式测量球体与圆盘之间的接触刚度;李玲等[13]等把润滑液刚度与固体表面接触刚度相结合得到新的法向接触刚度模型。
笔者基于分形理论,建立了平面正弦钢球传动机构中主动圆盘-钢球接触面的法向接触刚度模型。然后由固体接触面的接触刚度模型推导出润滑介质的接触刚度模型,由此实现粗糙接触面的固体接触刚度与润滑液的接触刚度相结合,得到平面正弦钢球传动机构在润滑作用下接触面法向接触刚度的计算模型,利用数值计算的方法归纳分析了相关参数对法向接触刚度的影响规律。
1 平面正弦钢球传动机构接触模型的建立
1.1 润滑作用下的接触状态
平面正弦钢球传动机构的传动元件主要包括:主、从动圆盘、保持架和钢球等[14],活齿钢球在正弦曲线形状的半圆轨道上转动,如图1所示。
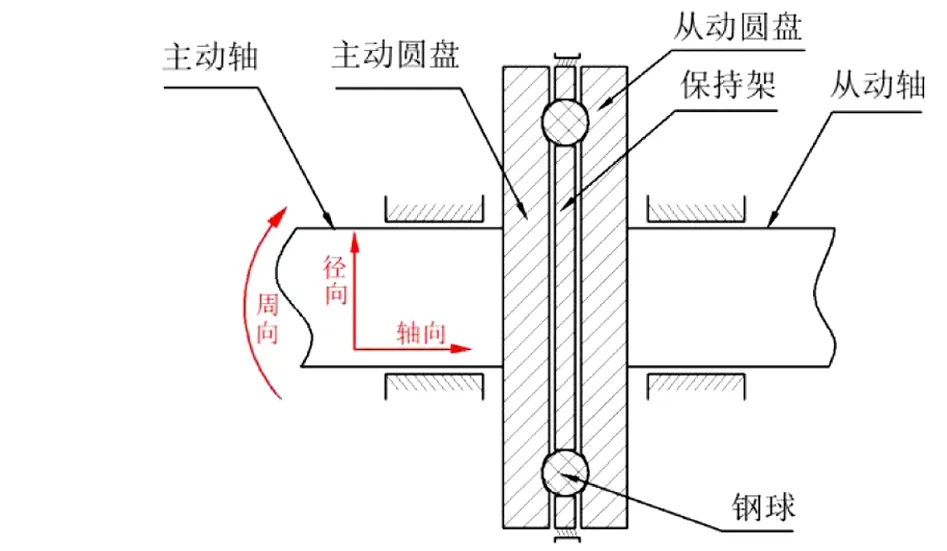
图1 平面正弦传动机构示意图
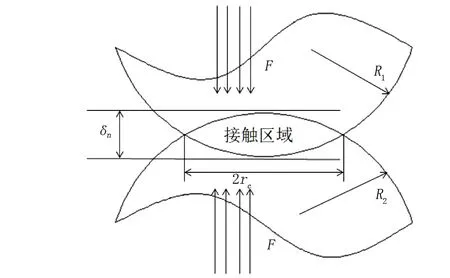
主、从动圆盘与活齿钢球之间均为球体与半圆轨道的接触形式,保持架与活齿钢球之间为球体与平面的接触形式,其中保持架可视为曲率半径趋近于无限大的圆形轨道。因此,主、从动圆盘-钢球及保持架-钢球的接触方式可以转化为钢球-半圆轨道接触形式的问题来分析,润滑作用下,他们之间的间隙由润滑液填充,如图2所示。
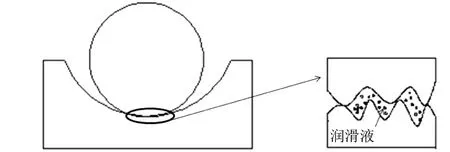
图2 润滑作用下钢球-半圆轨道接触示意图
将活齿钢球与其他传动原件的接触问题转化为粗糙球体与粗糙圆柱内切的模型,此时的接触区域已经由光滑的曲面接触转化为粗糙的曲面问题。该模型更加细化考虑了加工的真实面貌,更有利于接触特性的研究。
1.2 粗糙接触面分形接触表征
2个粗糙曲面接触可以等效为单粗糙面模型探究,如图3所示。粗糙面轮廓上的曲线可以由W-M函数表示[15]:
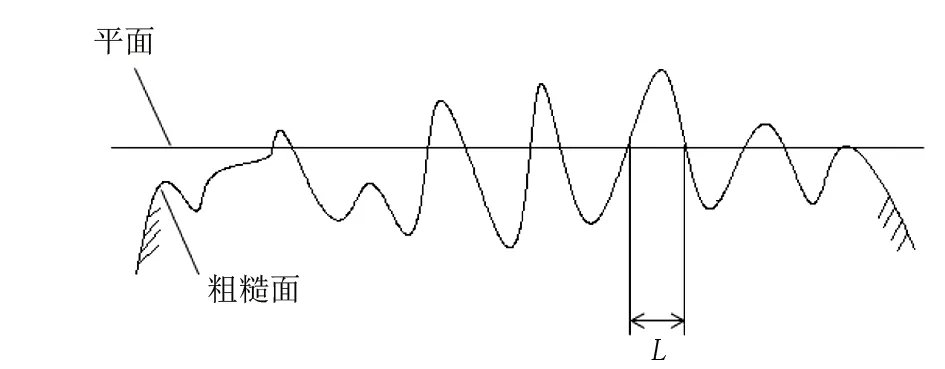
注:L为微凸体随机表面的采样长度。
(1)
式中:z(x)表示微凸体高度;x为轮廓位移坐标;D为接触面的分形维数;G为粗糙度幅值;γ为服从正态分布的随机接触表面,通常γ=1.5,nl为最低截止频率对应的序数。
可以看出z(x)由D、G、nl决定,D和G可以由W-M函数的功率谱获得。
1.3 粗糙接触面微凸体分布函数修正
M-B分形接触中微凸体的面积分布函数[15]:
(2)
式中:a为接触面微凸体面积;al为最大的接触面微凸体面积。
真实接触面积Ar为:
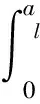
(3)
由临界接触点面积ac计算弹性接触面积Are和塑性接触面积Arp:
1)当al>ac时
弹性接触面积为:
(4)
塑性接触面积为:
(5)
总的接触面积为:
Ar=Are+Arp
(6)
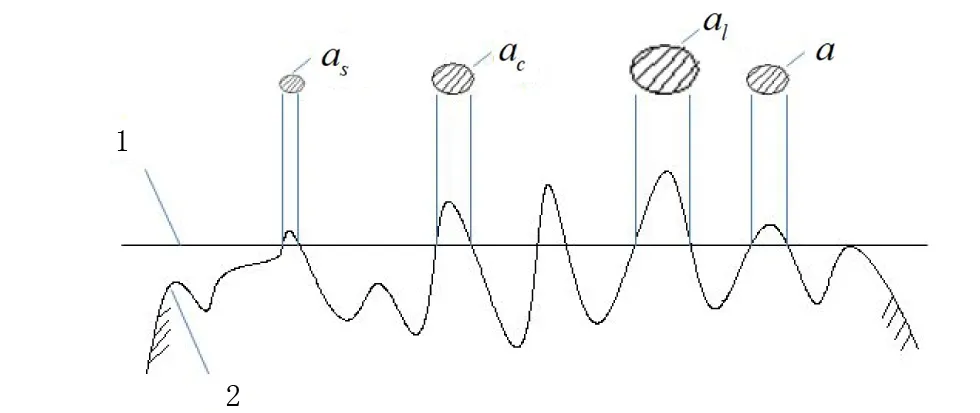
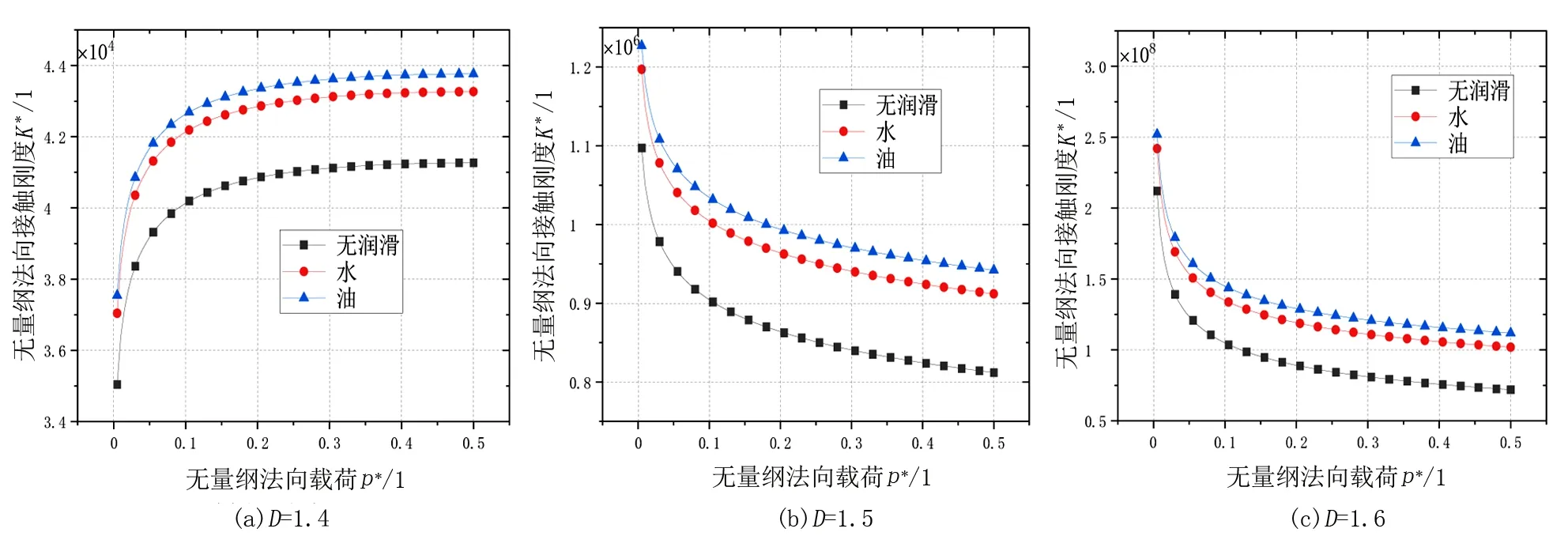
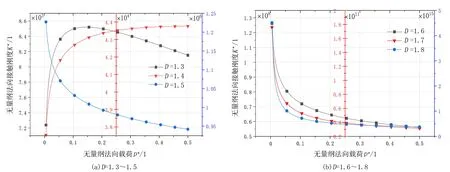
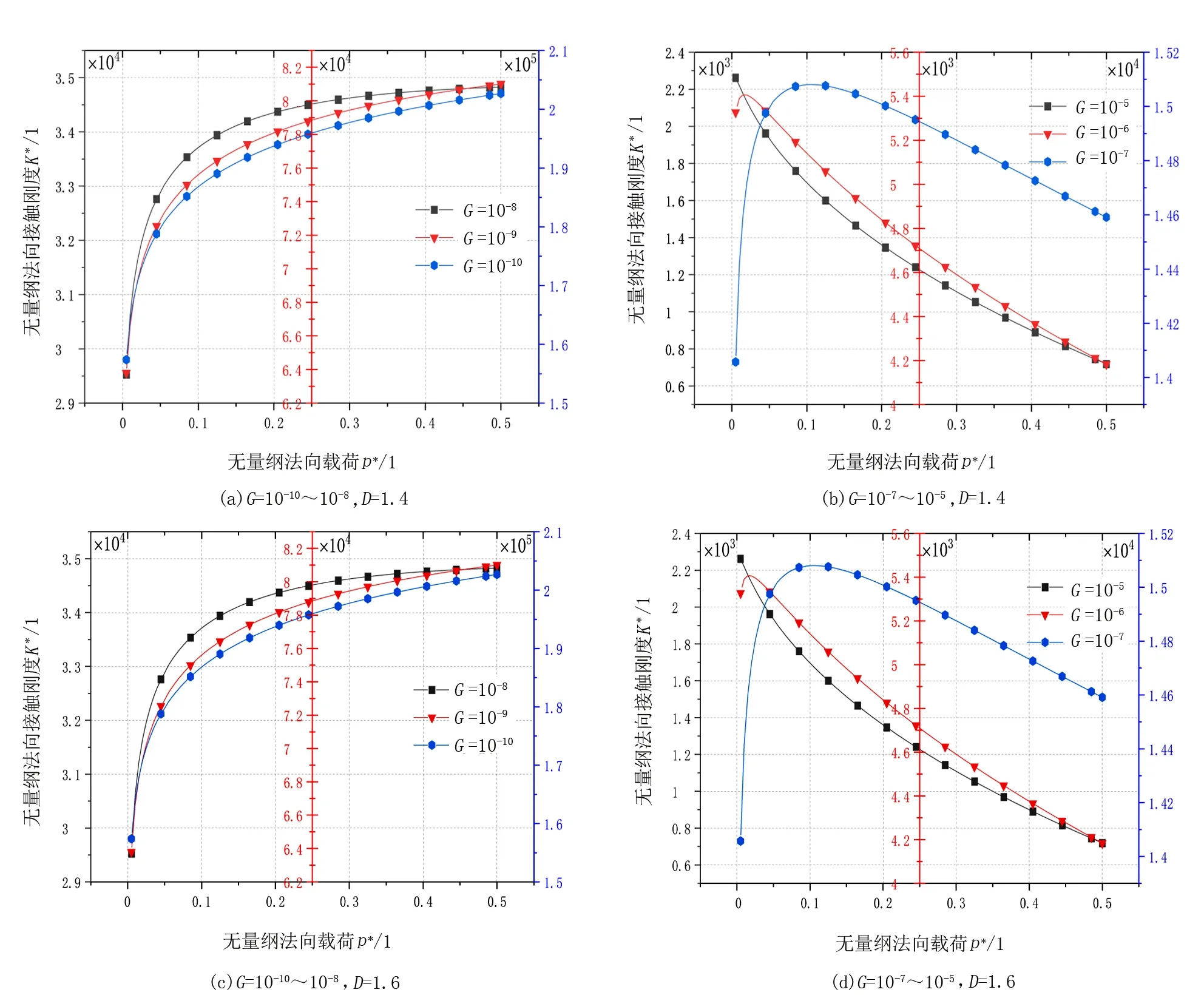
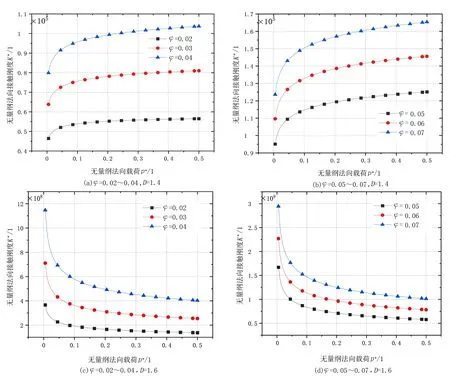
2)当al (7) 平面正弦钢球机构中的接触形式为曲面接触,若将分形模型合理地运用到传动机构的接触特性中去,需构造一个如图2所示接触形式的微凸体面积分布函数n(a)修正系数λ,修正后微凸体接触面积分布函数n′(a)为: n′(a)=λn(a) (8) 式中:λ为接触面修正系数。 根据微凸体面积分布函数n(a)可以构造出钢球-半圆轨道接触面微凸体面积分布函数的修正系数λ的函数表达式为: (9) 式中:R1为轨道半径;R2为钢球半径(假设R1>R2);Ee为综合弹性模量。 由图4可以看出,接触面修正系数λ随着钢球半径的增大呈现先增大而后趋于平缓的趋势,且λ不超过1。其原因在于随着钢球半径的增大,钢球与半圆轨道的曲率半径逐渐趋近于相等,此时钢球与半圆轨道的外轮廓互相包覆,两个表面接触面积增大。 图4 钢球半径与接触面修正系数λ关系 以单微凸体受力变形模型为研究切入点,基于分形接触理论推导出主动圆盘-钢球接触面微凸体弹塑性变形的临界面积计算公式,从而建立出主动圆盘-钢球固体接触面的法向接触刚度分形模型,然后利用固体表面的接触刚度模型建立润滑液的接触刚度模型。 2个半径为R1和R2的微凸体接触刚度模型,如图5所示。当法向载荷F作用到2个接触的微凸体上表面时,就会产生一个半径为rc法向位移量为σn的接触变形区域。 图5 单微凸体法向接触刚度模型 接触载荷与接触变形之间的关系表示为: (10) (11) (12) 式中:Re为主动圆盘-钢球的曲率系数;Ee为主动圆盘-钢球的综合弹性模量;a0为接触变形区域面积。 其中,Re和Ee的表达式分别为: (13) (14) 式中:E1和E2分别为主动圆盘和钢球材料的弹性模量;v1和v2分别为主动圆盘和钢球材料的泊松比。 根据式(10)、(11)和(12),单微凸体的法向接触刚度kn可以表示为: (15) 平面正弦钢球传动机构中主动圆盘-钢球接触面由无数个微凸体构成,在实际研究中,两粗糙接触面之间的研究问题简化为单粗糙面接触刚度模型,如图6所示。 注:a为微凸体的接触面积;as为微凸体最小接触面积;al为微凸体最大接触面积;ac为主动圆盘-钢球接触接触面微凸体发生弹塑性临界变形的面积;1为刚性平面;2为粗糙接触面。 平面正弦钢球传动机构中主动圆盘-钢球接触面为曲面,需引入前面所建立的修正系数λ,得到钢球-圆盘接触面载荷与真实接触面积之间的函数关系式[16]。 (16) (17) (18) (19) 2)当al≤ac时,微凸体发生塑性变形,接触面总载荷为: (20) 将单微凸体的法向接触刚度kn向多微凸体法向接触刚度进行推广,结合接触面微凸体分布函数n(a)对式(15)两边进行积分,可以得到: (21) 在式(21)中,最小微凸体接触面积 可以无限趋近于0。因此,式(21)可以改写为: (22) 假设主动圆盘-钢球接触面微凸体发生弹塑性临界变形的面积为ac,那么: 当al>ac时,主动圆盘-钢球接触面发生弹塑性变形; 当al≤ac时,主动圆盘-钢球接触面发生塑性变形,接触面刚度kn为0。 式(22)的积分将由0增大到ac,此时接触面微凸体法向接触刚度的计算式为: (23) 主动圆盘-钢球接触面微凸体临界接触面积ac与最大微凸体接触面积al的计算式为: (24) (25) 式中:kμ为摩擦力的修正因子;μ为摩擦系数。 将接触面微凸体分布函数n(a)以及接触面微凸体临界接触面积ac代入到式(23)中去,可得到主动圆盘-钢球接触面微凸体法向接触刚度公式为: (26) 主动圆盘-钢球接触面为曲面接触,因此还需要引入主动圆盘-钢球接触面微凸体分布函数n(a)的修正系数λ,将主动圆盘-钢球接触面微凸体分布函数修正为n′(a),其计算式为: (27) 将修正后的主动圆盘-钢球接触面微凸体分布函数n′(a)代入到式(26)中,可以得到主动圆盘-钢球接触面法向接触刚度的无量纲形式为: (28) 当主动圆盘-钢球接触面处于无润滑作用的状态下,接触面只有固体表面法向接触刚度,但是在润滑作用下,接触面的法向接触刚度由液体和固体两部分组成,假设粗糙接触面之间的空间充满润滑液,h为润滑液的厚度,F为施加的名义接触压力,因此润滑液的法向接触刚度可以定义为: (29) 假设润滑液内部没有切向应力,只有法向应力,体积模量B表示单位体积流体变化量引起的压力波动: (30) (31) 流体中的波速为: (32) 因此润滑液的接触刚度为: (33) 进一步简化计算,润滑液的等效厚度为: (34) 假设主动圆盘-钢球接触面的微凸体高度分布服从正态分布,则微凸体高度在z(x)=[-3σ,3σ]的概率为99.73%,因此接触面的初始距离可近似等于3σ,即d0=3σ;Δd为粗糙接触面的等效弹性变形量;Kn为主动圆盘-钢球固体接触面的法向接触刚度。 联立式(33)和式(34)可得润滑液的法向接触刚度为: (35) 对式(35)无量纲化: (36) 此时,在润滑作用下主动圆盘-钢球接触面的法向总接触刚度为: (37) 采用润滑介质的声学特性如表1所示,研究不同润滑液对主动圆盘-钢球接触面法向接触刚度的影响。 表1 润滑液材料的声学特性 图7所示为在不同分形维数下圆盘-钢球接触面不考虑润滑和不同润滑液下的法向接触刚度随无量纲法向载荷增加的变化曲线。由图7可以明显看出,圆盘-钢球接触面法向接触刚度受润滑作用影响较大,有润滑作用时接触面法向接触刚度明显比没有润滑介质时增加,润滑液的法向接触刚度随接触载荷的增加变化并不明显,并且润滑液为油的接触面法向接触刚度大于润滑液为水的接触面法向接触刚度,说明润滑液对主动圆盘-钢球接触面接触性能具有很重要的影响。 图7 不同润滑剂对主动圆盘-钢球法向接触刚度的影响 由于随着分形维数增加,表面将变得更加光滑,真实接触面积也逐步增大,法向变形量减少,提高了接触面的接触性能。但是法向接触刚度变化规律受分形维数影响较大,还需进一步探究分形维数变化对法向接触刚度的影响。 为了进一步探究分形维数对主动圆盘-钢球法向接触刚度的影响,由式(37)K*-D的关系,对D取不同的数值(D=1.3~1.8)来分析,公式中其他参数取值:G=10-9,φ=0.02,主动圆盘-钢球材料的硬度与屈服强度的相关系数K=2,弹性模量E=2.12×1011Pa,泊松比υ=0.3,摩擦系数μ=0.3。在传动机构转动一个周期的前提条件下得到图8所示分形维数对主动圆盘-钢球接触面法向接触刚度的影响规律。当D≥1.5时,接触面法向接触刚度随着法向载荷的增大先减小后保持不变。当D=1.3时,随着法向载荷增加,法向接触刚度先增大后减小,并且在p*<0.1增加速度较快。当D=1.4时,随着法向载荷增加,法向接触刚度先增大后不变,在p*<0.1增加速度也较快。通过数值计算发现,接触刚度在不同分形维数影响下呈现不同的变化趋势,K*与p*之间的关系受分形维数的影响如此之大,可能式(37)中大多数变量都存在D,如al,ac。分形维数D代表了主动圆盘-钢球半圆轨道微凸体的平整度,增大分形维数,真实接触面积也随之增大,法向变形量因此减少,法向接触刚度增加,接触面抗变形能力增大,有效地提高了接触面的接触性能。因此,通过改善主动圆盘半圆轨道的加工工艺,降低主动圆盘半圆轨道的粗糙度,可以有效提升主动圆盘-钢球接触面的接触性能。 图8 主动圆盘-钢球法向接触刚度与分形维数的关系 由式(37)K*-G的关系,对粗糙度幅值取不同的数值(G=10-10~10-5)进行数值计算,式中其他参数取值:φ=0.02,K=2,E=2.12×1011Pa,υ=0.3,μ=0.3,由于K*在不同分形维数D的影响下,随着p*的增大呈现不同的变化趋势,尤其以D≥1.5和D<1.5规律差异表现的尤为显著。因此,选取D=1.4和D=1.6在传动机构转动一个周期的情况下,研究粗糙度幅值G对主动圆盘-钢球接触面法向接触刚度的影响规律,如图9所示。 图9 主动圆盘-钢球法向接触刚度与粗糙度幅值的关系 当D=1.4时,随着p*的增大,K*在不同粗糙度幅值的影响下呈现不同的变化趋势;当G=10-10~10-8时,K*先增大然后保持不变;当G=10-7~10-6时,K*呈现先增大后减小的趋势; 当G=10-5,K*逐渐减小。同时,当p*保持不变,K*与粗糙度幅值呈递减关系。当D=1.6时,随着p*的增大,K*呈现先减小后趋于平稳的趋势。从整体来看,无论D=1.4还是D=1.6,当p*保持不变时,K*随着粗糙度幅值的增大而减小。 由图9可知,K*在不同粗糙度幅值下的变化规律会受到分形维数的影响。降低主动圆盘-钢球的接触面的粗糙度幅值,表面将变得更加光滑,真实接触面积增大,提高了接触面的接触性能。 根据式(37)中K*-φ的函数关系,对材料特性参数取不同的幅值(φ=0.02~0.07)进行数值计算。其他参数取值:G=10-9,K=2,E=2.12×1011Pa,υ=0.3,μ=0.3,由于分形维数影响接触面法向接触刚度与法向载荷之间的关系,在传动机构转动一个周期的前提下,取D=1.4和D=1.6分别研究材料特性参数对K*的影响规律,如图10所示。 图10 主动圆盘-钢球法向接触刚度与材料特性参数的关系 基于分形理论,建立在润滑作用下平面正弦钢球传动机构中主动圆盘-钢球接触面法向接触刚度模型,并利用数值分析的方法研究关键影响因素对接触面法向接触刚度的影响规律,得出以下结论: 1)主动圆盘-钢球接触面法向接触刚度受润滑作用影响较为明显,有润滑作用时接触面法向接触刚度明显提升,润滑液的法向接触刚度随接触载荷的增加变化并不明显,而与其材料特性和接触面分形参数有着密切影响关系。 2)分形维数D影响着主动圆盘-钢球接触面法向接触刚度与法向载荷的关系,以D=1.5为界限,其规律前后差异性表现尤为显著,在其他参数保持不变时,接触面法向接触刚度与分形维数呈递增关系。 3)其他参数保持不变,在一定法向载荷下,接触面法向接触刚度与粗糙度幅值G呈递减关系。因此,可以通过降低半圆轨道表面粗糙度来提升主动圆盘-钢球接触面的接触性能。 4)其他参数保持不变,在一定法向载荷下,接触面法向接触刚度与材料特性参数φ呈递增关系。对于软材料而言,弹性接触面积会随着φ的增加而增大,以此可以提升接触性能。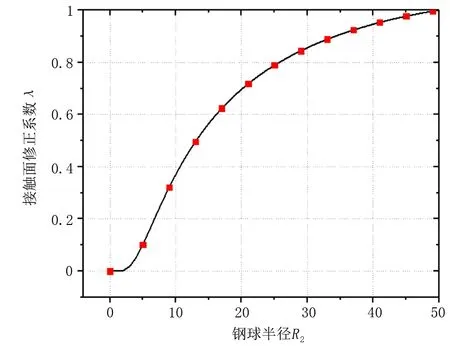
2 法向接触刚度模型的建立
2.1 单微凸体法向接触刚度模型
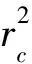
2.2 固体表面接触法向接触刚度模型
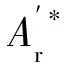
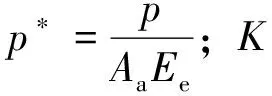
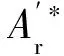
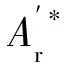
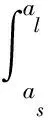
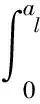
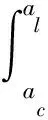
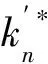
2.3 润滑液法向接触刚度
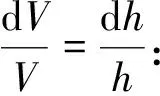
3 仿真结果分析
3.1 润滑液对法向接触刚度的影响

3.2 法向接触刚度与分形维数D的关系
3.3 法向接触刚度与粗糙度幅值G的关系
3.4 法向接触刚度与材料特性参数φ的关系
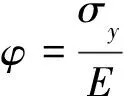
4 结论

