爆炸载荷作用下夹持方板动态响应量纲分析

王彦盛, 李伟兵, 于 良

爆炸载荷作用下夹持方板动态响应量纲分析

王彦盛1, 李伟兵1, 于 良2

(1. 南京理工大学 智能弹药技术国防重点学科试验室, 江苏 南京, 210094; 2. 山东特种工业集团有限公司, 山东 淄博, 255200)

爆炸载荷; 量纲分析; 夹持方板; 结构响应; 挠度厚度比

0 引言

随着反舰武器的迅速发展, 各种高性能反舰导弹已成为水面舰船最主要的水上威胁武器[1]。目前反舰导弹大部分采用半穿甲战斗部, 依靠弹体动能穿透舰船舷侧外板, 后通过智能引信使战斗部在舰船内部爆炸, 这时爆炸直接作用于舰船结构、设备和人员, 将对舰船生命力产生极大的威胁[2-3]。因此, 研究爆炸载荷作用下结构的动态响应, 对于爆炸结果分析、爆炸响应预测和抗爆结构设计等领域非常重要[4-5]。Geretto等[6]对不同约束条件下爆炸载荷对不同厚度靶板的最终变形量进行了试验研究, Yao等[7]对箱形结构内爆导致的壁面变形量进行了研究。

文中通过对前人的试验数据进行分析, 得出了适用于试验数据的无量纲数, 发现夹持方板的结构响应与所得到的无量纲数有较好的线性关系, 可为研究舱室密闭容器动态结构响应提供参考。

1 夹持方板模型

密闭容器内部爆炸的动态结构响应是许多学者广泛关注的问题, 其中涉及船舱内爆所导致的舱壁变形可以等效为爆炸载荷作用下矩形板动态响应问题, 先研究单一板在爆炸载荷作用下的变形情况, 并由此推广至舱室内爆情况。文中使用量纲分析方法对夹持方板在爆炸载荷作用下的变形情况进行分析。

1.1 理论模型

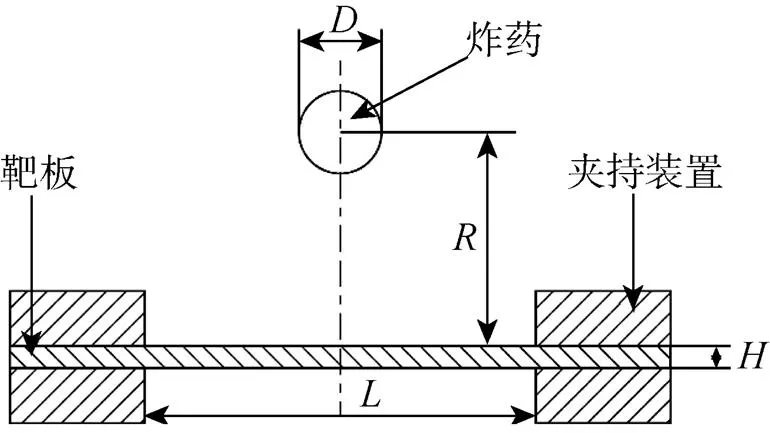
图1 夹持方板示意图

1.2 物理量分析

表1 独立物理量列表

2 量纲分析

以矩形板挠度为因变量, 给出其相关的函数表达式为

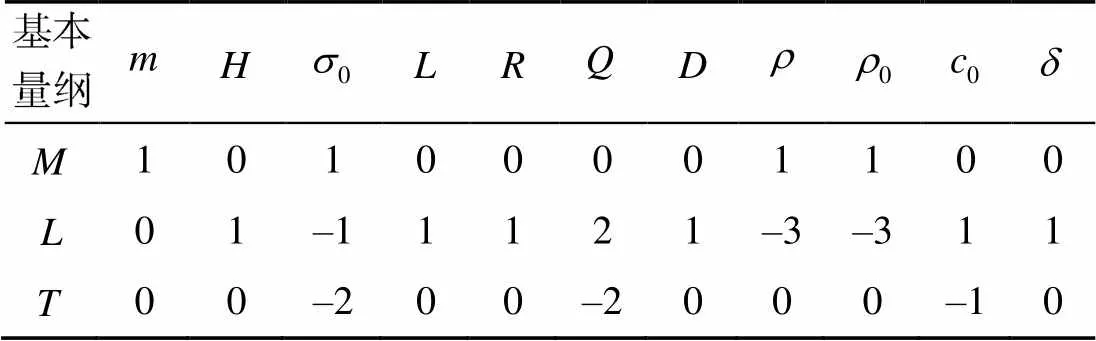
表2 爆炸载荷作用下矩形板变形变量的量纲幂次系数

对表2进行类似矩阵初等变换, 可以得到表3。

表3 爆炸载荷作用下矩形板变形变量的量纲幂次系数(初等变换)

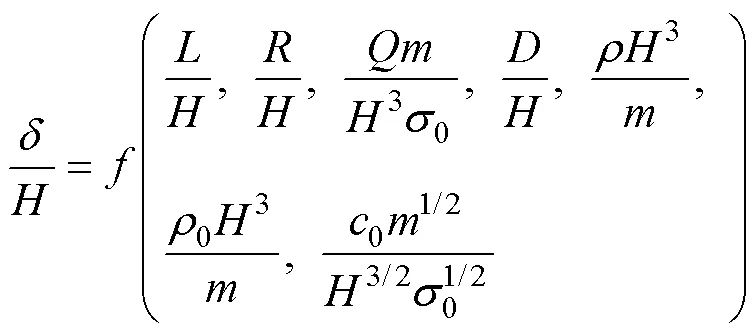
皇窑景区本着“立足景德镇、走出江西省、面向中国、放眼全世界”的发展目标，参考GB/T 24421—2009《服务业组织标准化工作指南》系列国家标准，遵循“分块负责、齐头并进，先建立、后细化整合”的标准化工作方针和“简化、统一、协调、优化”的标准化原则，突出陶瓷文化创意特色的相关内容，建立覆盖全景区的服务标准体系。

此时式(2)可以写为

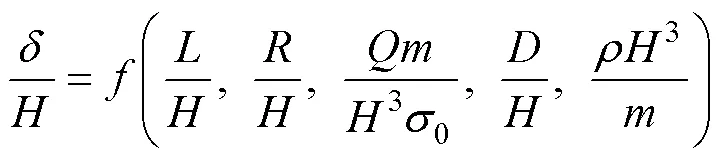
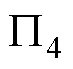
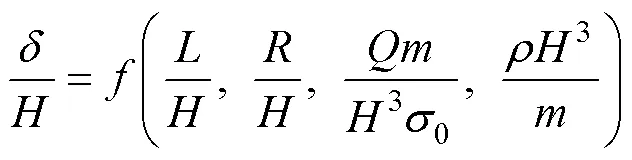
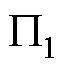
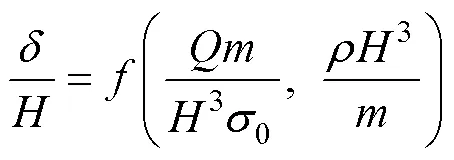
若模型中炸药、金属板材料与原型中对应一致, 则有

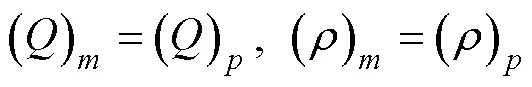
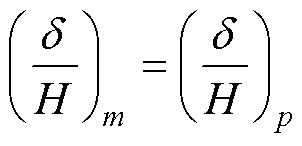
当模型与原型满足几何相似时, 式(2)可以写为

3 试验数据分析

图2 试验布置示意图

图3 试验板变形横截面图

表4 实验方案与最终变形结果

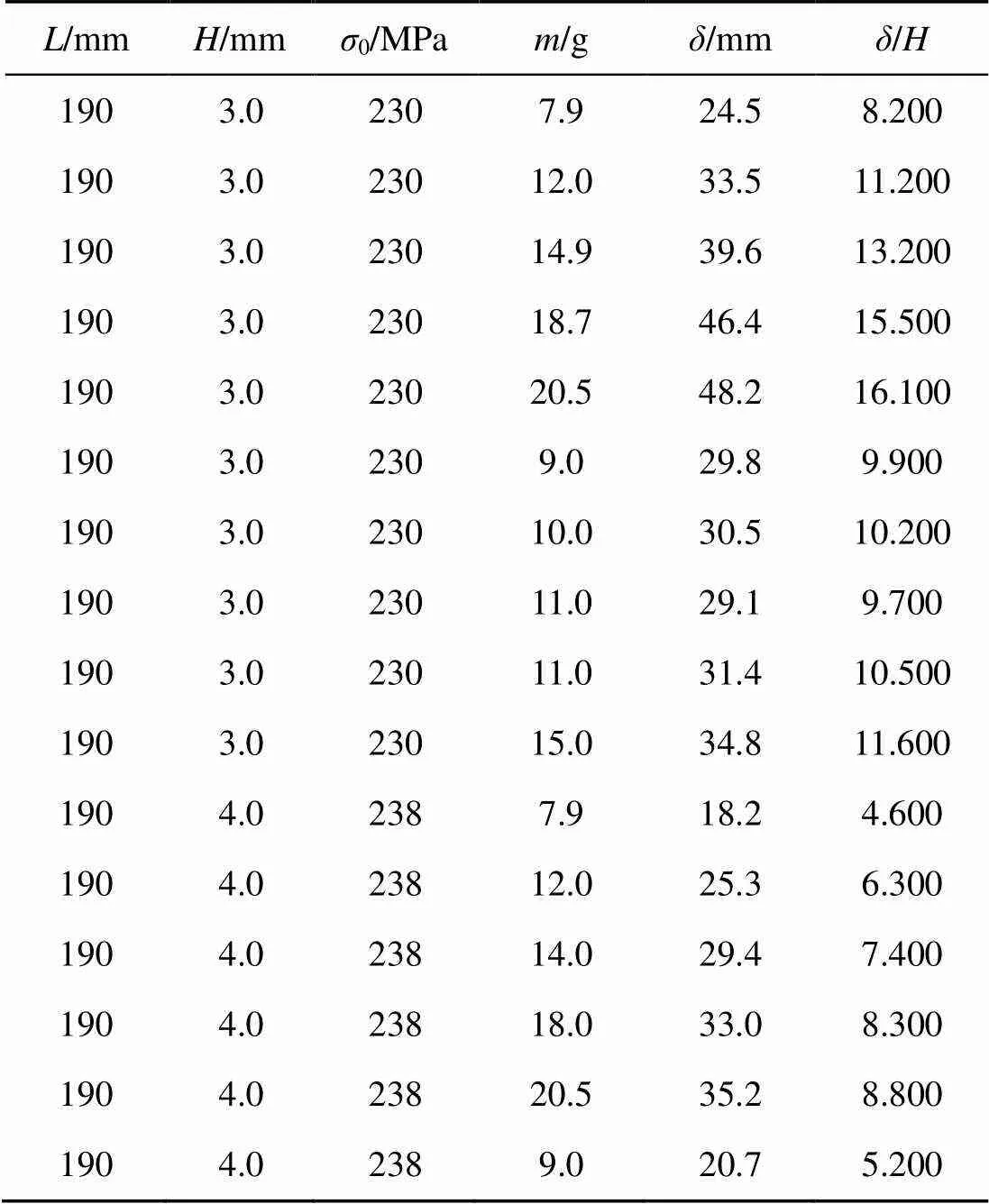
续表

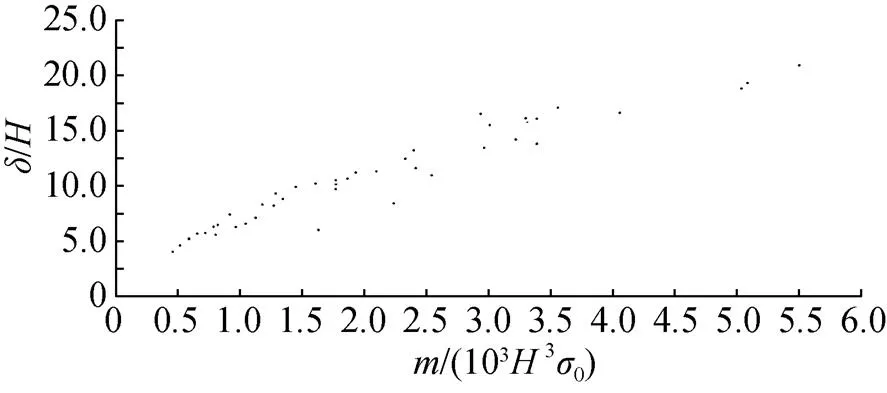
图4 爆炸载荷作用下夹持方板无量纲弯曲变形

4 结论

文中使用量纲分析对夹持方板在爆炸载荷作用下的动态响应问题进行了研究, 推导了靶板结构动态响应中变形量的无量纲挠度厚度比, 使用文献中公布的试验对所得到的结论进行了拟合, 由于试验数据的限制, 故没有考虑炸药爆距和靶板大小对变形量的影响, 对此还需进一步研究。当满足文中所假设的条件时, 靶板的变形量与文中所给出的无量纲数呈线性关系。主要结论如下。

3) 基于文中量纲分析所得表达式可以快速预测爆炸载荷作用下靶板的最大变形量, 可用于爆炸作用下舱室模型舱壁的毁伤特性研究, 为舰船毁伤研究提供参考。

[1] 朱锡, 张振华, 梅志远, 等. 舰船结构毁伤力学[M]. 北京: 国防工业出版社, 2013.

[2] 浦金云, 金涛, 邱金水, 等. 舰船生命力[M]. 北京: 国防工业出版社, 2009.

[3] 杨卫丽, 耿国桐, 李秋娜, 等. 国外反舰导弹发展初步分析[J]. 战术导弹技术, 2014(3): 1-5.

Yang Wei-li, Geng Guo-tong, Li Qiu-na, et al. Research on the Development of Overseas Anti-ship Missile[J]. Tactical Missile Technology, 2014(3): 1-5.

[4] Zhang D, Yao S J, Lu F Y, et al. Experimental Study on Scaling of RC Beams Under Close-in Blast Loading[J]. Engineering Failure Analysis, 2013, 33: 497-504.

[5] Wang W, Zhang D, Lu F Y, et al. Experimental Study and Numerical Simulation of the Damage Mode of a Square Reinforced Concrete Slab Under Close-in Explosion[J]. Engineering Failure Analysis, 2013, 27: 41-51.

[6] Geretto C, Yuen S C K, Nurick G N, et al. An Experimental Study of the Effects of Degrees of Confinement on the Response of Square Mild Steel Plates Subjected to Blast Loading[J]. International Journal of Impact Engineering, 2015, 79: 32-44.

[7] Yao S J, Zhang D, Lu F Y. Dimensionless Number for Dynamic Response Analysis of Box-shaped Structures under Internal Blast Loading[J]. International Journal of Impact Engineering, 2016, 98: 13-18.

[8] Zhao Y P. Suggestion of a New Dimensionless Number for Dynamic Plastic Response of Beams and Plates[J]. Archive of Applied Mechanics, 1998, 68(7-8): 524-538.

[9] Bridgman P W. Dimensional Analysis[M]. New Haven: Yale University Press, 1922.

[10] Johnson W. Impact Strength of Materials[M]. London: Edward Arnold, 1972.

[11] Johnson W, Sengupta A K, Ghosh S K, et al. Mechanics of High Speed Impact at Normal Incidence between Plasticine Long Rods and Plates[J]. Journal of the Mechanics and Physics of Solids, 1981, 29(5-6): 413-445.

[12] Zhao Y P. On Some Dimensionless Numbers in Fracture Mechanics[J]. International Journal of Fracture, 1997, 83: 7-13.

[13] 张振华, 陈平毅, 漆万鹏, 等. 舰船局部板架结构在水下爆炸冲击波下动态响应的相似律研究[J]. 振动与冲击, 2008, 27(6): 81-86.

Zhang Zhen-hua, Chen Ping-yi, Qi Wan-peng, et al. Scaling Law of Dynamic Response of Stiffened Plates for a Ship Subjected to under Water Shock[J]. Journal of Vibration and Shock, 2008, 27(6): 81-86.

[14] 高光发. 量纲分析基础[M]. 北京: 科学出版社, 2020.

[15] Jacob N, Yuen S C K, Nurick G N, et al. Scaling Aspects of Quadrangular Plates Subjected to Localised Blast Loads—Experiments and Predictions[J]. International Journal of Impact Engineering, 2004, 30(8-9): 1179-1208.

[16] Teeling-Smith R G, Nurick G N. The Deformation and Tearing of Thin Circular Plates Subjected to Impulsive Loads[J]. International Journal of Impact Engineering, 1991, 11(1): 77-91.

[17] Olson M D, Nurick G N, Fagnan J R. Deformation and Rupture of Blast Loaded Square Plates—Predictions and Experiments[J]. International Journal of Impact Engineering, 1993, 13(2): 279-291.

Dimensional Analysis of the Dynamic Responses of Clamped Square Plates under Explosion Loads

WANG Yan-sheng1, LI Wei-bing1, YU Liang2

(1. ZNDY of Ministerial Key Laboratory, Nanjing University of Science and Technology, Nanjing 210094, China; 2. Shandong Special Industry Group Co., Zibo 255200, China)

explosion load; dimensional analysis; clamped square plate;structural response; deflection-thickness ratio

王彦盛, 李伟兵, 于良. 爆炸载荷作用下夹持方板动态响应量纲分析[J]. 水下无人系统学报, 2022, 30(3): 378-383.

TJ6; U662.2

A

2096-3920(2022)03-0378-06

10.11993/j.issn.2096-3920.2022.03.014

2022-04-20;

2021-05-22.

国家自然科学基金(11972018).

王彦盛(1998-), 男, 在读博士, 主要研究方向为武器工业与军事技术.

(责任编辑: 吴 攀)