基于Finsler引理的一类连续时间多时滞系统稳定性分析

廖永龙，宋嘉琪

(北京石油化工学院数理系， 北京 102617)

稳定性是控制系统理论的一个重要特性，所谓稳定性是指在各种外部和内部因素的干扰下，系统保持预定运行或正常工作状态能力的一种度量。

稳定性问题实质上是控制系统自身的属性问题，在大多数情况下，稳定是系统正常运行的前提条件[1]。在实际系统中，过去状态往往不可避免地对当前的状态产生影响，即系统的演化趋势不仅依赖于系统当前的状态，也依赖于过去某一时刻或多个时刻的状态，这类系统称为时滞系统。时滞常见于传染病和流行病模型[2]、神经网络[3]、机械控制系统[4]等领域。连续时间域中的时滞系统是无穷维系统，有无穷多个特征根[5-6]，这给系统的稳定性分析和控制器设计带来很大的困难和挑战。因此，时滞系统无论在理论分析还是在工程实践中都是一个研究热点。

线性时滞系统的稳定性分析方法主要有谱理论、代数系统理论、泛函微分方程理论等[7-12]。尽管对定常时滞系统的精确稳定性问题的研究较多，但是目前还未建立起成体系的理论将定常时滞系统的稳定性判据推广到时变时滞系统，时变时滞系统的稳定性一直是一个开放的问题[13]。Lyapunov-Krasovskii泛函法(LKF)是一种研究时变时滞系统的主要方法，由Krasovskii于20世纪50年代末提出，通常由一个线性矩阵不等式表示。在不等式的放缩过程中，Jensen不等式发挥着重要的作用[14]。此外，Wirtinger积分不等式和Auxiliary积分不等式也经常用于不等式的放缩[15-16]。

由于Lyapunov-Krasovskii方法高度依赖于泛函的构造，而时滞个数的增加又相应地增加了泛函构造的难度。通过引入冗余方程对时滞系统重新表示，可简化Lyapunov-Krasovskii泛函的构造，并且可有效降低稳定性判据的保守性[17]。文献[18-19] 中的研究结果表明，基于Finsler引理可有效降低判别矩阵的阶数。

笔者将基于Finsler引理考虑多个时滞的情形，特别地以2个时滞为代表进行研究，给出稳定性定理，并构建新的Lyapunov-Krasovskii泛函，然后用线性矩阵不等式进行证明。

1 问题的数学描述和基本引理

考虑连续时间状态时滞系统：

(1)

其中：x(t)∈Rn表示系统的状态向量；hi(t)(i=1，2)表示时间的滞后量，并且满足：

0≤h1(t)≤h2(t)≤hm

(2)

(3)

这里的常数hm>0，表示滞后量的最大值;常数d≥0，表示滞后量变化率的最大绝对值。函数φ(θ)(θ∈[-hm，0] )是初始状态，A，A1，A2∈Rn×n均是常数矩阵。

将讨论时变时滞系统(1)的稳定性问题。首先，给出下述3个引理：

引理1[1](Lyapunov稳定性定理)对于n维自治系统：

引理2[11](Jensen不等式)对于任意的常数矩阵M∈Rn×n，M=MT>0，标量γ>0，向量函数ω:[0，γ] →Rn，若下述各积分存在，则有如下不等式成立：

引理3[17](Finsler引理)设B∈Rn×pn，Γ∈Rpn×pn为对称矩阵，对任意满足Bx=0的非零向量x∈Rpn，xTΓx<0当且仅当矩阵B⊥TΓB⊥<0(表示该矩阵负定)，其中B⊥表示B的任意右正交补。

2 主要结果

给出系统(1)的渐近稳定性定理，并构造Lyapunov-Krasovskii泛函对定理进行证明。

定理1对于给定的标量hm>0和d≥0，以及满足条件(2)～(3)的时变时滞hi(t)，i=1，2，系统(1)渐近稳定的充分条件是:存在n阶正定矩阵P、Qi(i=1，2，3)、R使得线性矩阵不等式：

S⊥TΓS⊥<0

(4)

成立，其中

(5)

(6)

矩阵Γ中的Wi(i=1，2，3，4)表示如下：

其中：S⊥表示S的右正交补。

证明:构造Lyapunov-Krasovskii泛函如下:

(7)

因为矩阵P、Qi(i=1，2，3)、R均为正定矩阵，所以V(x)≥0。对式(7)关于t求导，得

xT(t)Q1x(t)-xT(t-h1(t))Q1x(t-h1(t))×

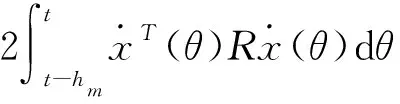
(8)

根据引理2可知

x(t-h(t)]

于是

x(t-h1(t))]

(9)

因为t-h2介于t-hm到t之间，所以有

(10)

结合式(8)～式(10)和式(3)可得：

xT(t-h1(t))Q1x(t-h1(t))(1-d)+

xT(t)Q2x(t)-xT(t-h2(t))Q2x×

(t-h2(t))(1-d)+xT(t)Q3x(t)-

x(t-hm)] -[x(t)-x(t-h1(t))]T×

(11)

令

(12)

式(11)可记作

(13)

其中，Γ由定义(6)给出。

此外，利用式(5)和式(12)可以将系统(1)重新记作：

Sξ(t)=0

(14)

根据引理1可知，如果对于满足方程(14)的所有ξ(t)不等式：

ξT(t)Γξ(t)<0

(15)

均成立，那么原系统(1)渐近稳定。根据引理3可知，不等式(15)等价于不等式(4)，定理得证。

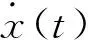
3 稳定性条件的进一步讨论

系数矩阵S∈Rn×5n的正交补S⊥∈R5n×4n，于是对式(4)作进一步的化简。取S的正交补：

则有

其中，

分别对U2和U3作如下分解：

则可得到如下简化后的稳定性定理。

定理2给定标量hm>0和d≥0，对于任意满足条件(2)～(3)的时变时滞hi(t)，i=1，2，系统(1)渐近稳定的充分条件是存在n阶正定矩阵P、Qi(i=1，2，3)、R使得矩阵负定。

(16)

依据定理2可直接通过矩阵不等式来判断时滞系统的稳定性。

4 数值仿真

通过2个数值算例对所得结论进行验证。

取正定矩阵P=10，R=1，Q1=0.1，Q2=0.1，Q3=1。计算得矩阵Ψ的特征值依次为λ1=-40.322 4，λ2=-6.731 4，λ3=-4.028 3，λ4=-0.527 8，即可判断出矩阵Ψ负定。仿真结果(如图1所示)也表明系统的零解渐近稳定。

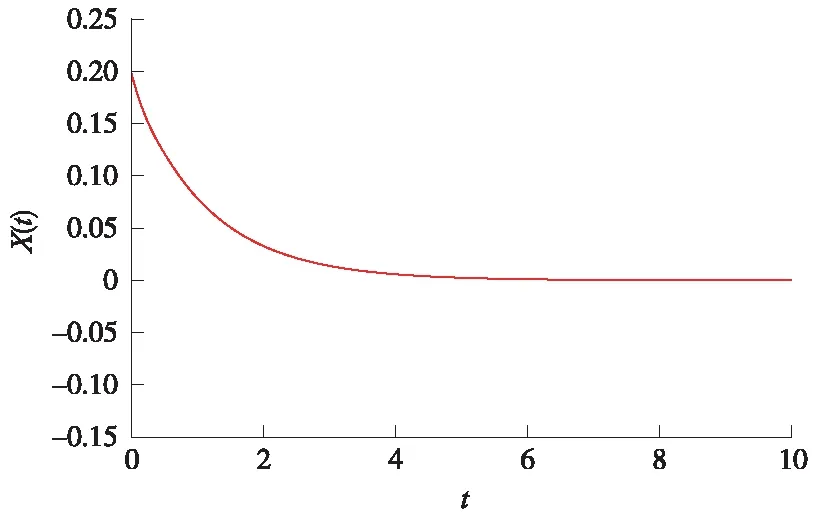
图1 一阶系统的状态轨迹Fig.1 State trajectory of the first order system

例2(二阶系统)考虑系统(1)，设其系数矩阵分别取为：

取正定矩阵

计算得矩阵Ψ的特征值依次为λ1=-168.040 5，λ2=-12.209 7，λ3=-10.654 5，λ4=-10.202 0，λ5=-1.712 5，λ6=-0.369 4，λ7=-0.011 7，λ8=-0.078 5。即可判断出矩阵Ψ负定。仿真结果(如图2所示)也表明系统的零解渐近稳定。

图2 二阶系统的状态轨迹Fig.2 State trajectories second order system

2个数值算例仿真结果表明，对于变时滞系统(1)，若存在正定矩阵P、Qi(i=1，2，3)、R使得二次型矩阵Ψ负定，即可知系统的零解渐近稳定。

5 结论

讨论了具有多个时变时滞的连续时间线性系统的稳定性问题，特别地，以2个时滞为例进行了研究。基于Finsler引理给出了这类系统的稳定性定理，并构造Lyapunov-Krasovskii泛函给出定理的证明。证明过程表明，若对于给定的最大滞后量系统稳定，则对小于该滞后量的时变时滞系统是否稳定还与其滞后量的变化速率有关，这是与常时滞系统的不同之处。此外，分析了正交补矩阵的结构，对稳定性条件做了进一步的简化。成功地将现有文献中的结论推广到多个时变时滞的情形。最后通过2个数值算例验证了结论的有效性。