变桨轴承螺栓连接建模方法及力学性能研究

朱 盟，张洪伟，窦艳涛，高 师，曹 钢

(北京石油化工学院机械工程学院，北京 102617)

随着我国风电产业的不断发展，截止2020年我国风电机组装机总容量超2.2亿kW，稳居世界首位。在风电传动系统中变桨轴承是必要零件，在风机单机发电量不断增加的背景下，变桨轴承所承受的工况更加恶劣，而螺栓是变桨轴承安全可靠运行20年的基础条件，要求其屈服强度高、螺栓等级高(10.9级或12.9级)、结构尺寸大，因此在风电机组中所使用的螺栓是一种高强度螺栓，螺栓连接一直是风电机组研究的重要部分[1-2]。风电机组中螺栓失效会造成严重的后果，而在风电机组中常见的失效形式有断裂和变形脱扣，断裂又分为螺纹根部断裂和螺头断裂。

目前国内外学者的研究主要集中在变桨轴承自身结构或采用Hertz理论来研究载荷分布对力学性能及寿命的影响，而对于螺栓连接对变桨轴承力学性能的影响研究较少。Vadean等[3]分析研究了螺栓连接在复杂外载荷下对变桨轴承力学性能的影响，基于二维模型中轴向刚度来控制螺栓连接性能的局部刚度。Aguirrebeitia等[4]基于赫兹接触理论计算，简化滚珠接触，将滚珠挤压变形等效简化为非线性弹簧单元与梁单元的组合，有利于仿真的收敛性。并研究了滚珠承载能力对轴承的力学性能影响。Yuan等[5]基于变桨轴承内圈与桨叶的螺栓连接关系，建立多种螺栓连接仿真模拟，并仿真得到螺栓应力和螺纹接触应力的精确分析结果，并提出了变桨轴承螺栓连接的有限元分析方案。石秀勇等[6-7]进行了螺纹连接的细节建模分析，均为单螺栓连接，不适用于螺栓组连接。考虑了摩擦系数，大大降低了风电系统的螺栓组有限元计算效率。Musto[8]研究高强度螺栓在不同材料的连接件之间刚度的影响关系，并运用有限元的方法得出了螺栓的有效刚度公式。Tomohiro NARUSE等[9]运用VDI 2230高强度螺栓连接理论与有限元分析相结合的方法，验证等效锥形压应力场，可以做为有限元计算理论支撑。史文博等[1]采用等效梁模拟螺栓连接，可以减少计算成本，但在计算螺旋副轴向径向接触刚度时存在误差。

针对以上螺栓连接建模方案中存在的问题，笔者依据VDI2230准则为理论基础，对高强度螺栓连接建模方法进行了研究，提出一种适用于变桨轴承螺栓组的建模方案；在此基础上，建立了变桨轴承螺栓有限元模型，分析其预紧力大小对变桨轴承应力结果的影响。

1 变桨轴承螺栓模型

变桨轴承所处的工作环境恶劣，受径向力(Fr)、轴向力(Fa)、倾覆力矩(M)复杂工况的影响，如图1所示，轴承内圈直径2.7 m，外圈直径3.2 m，内圈分布112个M39的螺栓与叶片连接，外圈分布118个螺栓与叶片连接。

图1 变桨轴承及其载荷图Fig.1 Pitch bearing and load diagram of pitch shaft

1.1 理论计算模型

为便于进行螺栓的理论计算，基于图1变桨轴承结构受力图建立单螺栓的理论计算模型，利用VDI2230进行理论计算，结果如图2所示。VDI2230是德国工程师协会发布的指南，主要用来计算校核螺栓连接的安全性。此方法用于工程实践已超过25年，对于螺栓连接的计算给出理论计算准则[10]。

图2 单螺栓连接计算模型Fig.2 Calculation model of single bolt connection

螺栓连接计算模型中，由2块圆柱板组成，上圆柱板为盲孔，下圆柱板为螺纹孔。初始条件为同心夹紧且同向加载，表面压力为5 MPa。取M12×80 mm螺栓为研究对象，螺栓具体尺寸根据DIN EN ISO准则进行建模。

运用VDI2230准则对单螺栓连接进行理论计算，通过对实际工况的分析，在模型中取出其中最危险的螺栓连接进行有限元建模分析，并与理论结果比对分析。

1.2 计算结果

单螺栓受力图如图3所示，对于同心加载计算最大轴向载荷和横向载荷，通过扭矩扳手加载的方式，并根据VDI223准则中表A7确定螺栓强度等级为12.9级。螺栓最大轴向载荷、横向载荷和螺栓最大装配载荷的计算式分别为：

图3 单螺栓载荷图Fig.3 Load diagram of single bolt

FAmax=Pmax×A=23.55 kN

(1)

FQ=0

(2)

FMmax=63 000 N

(3)

式中：FAmax为最大轴向载荷;Pmax为表面压力;A为上板承压面积;FQ为横向载荷；FMmax为最大装配载荷。

使用扭矩扳手和相对较大的夹紧长度比(lk/d=3.6)，对于摩擦系数等级B，根据规范表A8得到拧紧系数αA=1.8。

此螺栓连接为对称夹紧(Ssym=0)和同心加载(a=0)。因此得到最小夹紧载荷：

FKerf=FKRmin=103

(4)

式中：Ssym为螺栓轴线与横向变形体轴线距离；a为轴向载荷FA的作用线与横向对称变形体的轴向距离；FKerf为最小夹紧载荷；FKRmin为分界面残余夹紧载荷。

根据VDI2320 part1 5.1.1中的公式，确定螺栓弹性回弹量为：

δS=δSK+δi+δGew+δGM=5.796×10-6mm/N

(5)

式中：δSK为螺栓头部弹性回弹量；δi为任何部分i的弹性回弹量；δGew为加载旋合螺纹弹性回弹量；δGM为旋合螺纹和螺母弹性回弹量。

同心夹紧件回弹量δp由VDI2230准则公式(40)计算，则

δp=0.872×10-6mm/N

(6)

由准则可知本模型夹紧部件补充回弹量δpzu与变形螺纹牙体弹性回弹量δM相等，因此载荷系数∅K为：

(7)

由准则可知螺栓连接类型为SV4，确定载荷引入系数n=0.35，因此，确定载荷系数∅n为：

∅n=n·∅k=0.35×0.156=0.054 6

(9)

对于现有轴向载荷和粗糙度RZ=16，由准则中表5给出了每种情况下螺纹中3 μm、头部支承区域3 μm和分界面2 μm的嵌入，因此总嵌入量fz为：

fz=3+3+2=8×10-3mm

(10)

因此预加载荷损失为：

(11)

确定最小预加载荷FMmin为：

FMmin=FKerf+(1-∅n)FAmax+FZ+

(12)

因此，最大装配预紧载荷为：

FMmax=αA×FMmin=48 458 N

(13)

从VDI2230准则的表A1获得要求最小屈服点90%利用率和螺纹中最小摩擦系数μGmin=0.1，强度等级为10.9，螺栓的许用装配预加载荷FMzul为：

FMzul=FMTab=64.8 kN

(14)

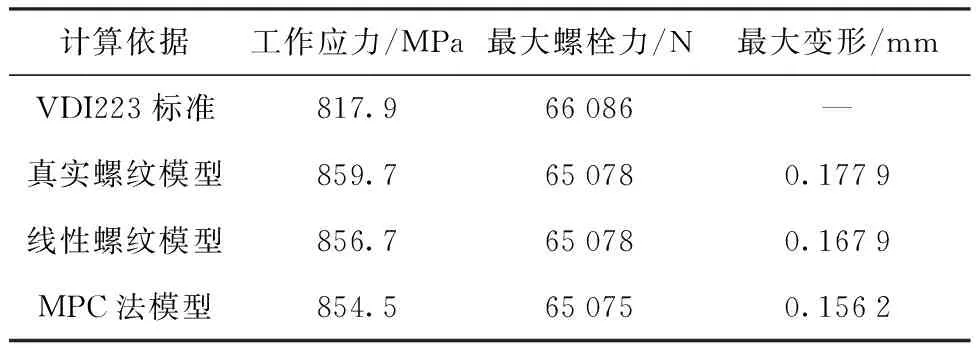
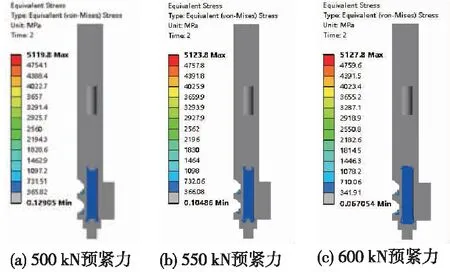
由于FMmax

根据VDI2230准则计算螺栓的工作应力[10]：

FSmax=FMzul+∅n×FAmax=66 086 N

(15)

σzmax)=FSmax/AS=783.9 N/mm2

(16)

58 700 N·mm

(17)

(18)

(19)

817.9 N/mm2

(20)

σred，B

(21)

(22)

式中：FMTab为装配预加载荷；FSmax为最大螺栓载荷；σzmax为螺栓最大拉伸应力；MG为螺栓拧紧扭矩；WP为抗扭截面模量；τmax为最大扭转应力；σred，B为等效应力；RP0.2为螺栓0.2%规定应力；SF为安全系数。

通过VDI2230规范计算了单螺栓的理论结果。通过计算得出单螺栓装配预紧力，给出了螺栓连接正常工作时螺栓的预紧力范围，并得到相应情况下的螺栓应力。其中最小预紧力是保证法兰连接不发生分离、滑动以及翘曲等情况的安全预紧力下限，可以用作极限拉压载荷作用下的螺栓状态验证；螺栓的装配预紧力可以为工程实践提供参考，也是有限元仿真参数设置和结果比对的重要依据。

2 螺栓连接的有限元建模方法

采用VDI2230中的相关理论建立了单螺栓的等效刚度数值计算模型，得出了合适的螺栓连接相应的数据参数，并计算出在一定工况下的最大拉伸应力、最大切应力、接触面压力等数据。采用有限元技术并依据上一节设计得到的单螺栓模型，建立不同的有限元分析模型。最后提取有限元仿真结果与VDI2230理论结果进行比较分析，得出螺栓建模的简化方法。

2.1 真实螺纹有限元模型

这种方法是最精确的螺栓模拟，真实螺纹模型如图4所示。螺纹的详细建模在模型中提供了准确的线程行为[11]。在螺纹区域需要非常精细的网格离散化，并且需要设置螺纹处的摩擦约束，而在有限元计算中，每增加一处摩擦约束，就会使计算效率降低。以某MW级的风电轴承为例，拥有208个螺栓，因此需要增加208对摩擦接触，导致计算效率低，所以在螺栓组连接中不建议使用真实螺纹建模，但是该模型适用于螺纹根部断裂破损和螺纹变形脱扣问题的研究，能够很好地研究螺纹根部裂纹的产生和扩展。

图4 真实螺纹模型Fig.4 Real thread model

2.2 截面螺纹有限元模型

在该方法中，通过将模拟螺栓螺纹赋予在螺纹接触区域的螺栓表面，按真实螺纹的参数设定螺距(p=1.75 mm)、螺纹旋入长度(l1=33 mm)、螺纹升角(β=60°)，这样就构成线性螺纹。该方法可以减少螺纹处的网格离散化问题，且接近真实螺栓连接。该方法需要在网格划分时，在螺纹区域的网格为螺距p的一半[9]，划分后的网格模型如图5所示。该模型适用于研究螺杆断裂破损相关问题。

图5 截面螺纹模型Fig.5 Section thread model

2.3 MPC法有限元模型

MPC(Multipoint coupling)是指多点耦合，在螺栓连接处直接采用绑定耦合的简单建模方法，如图6所示。该方法提供了一种接近真实螺栓模型精度的结果，但不需要详细的螺纹几何形状和精细的网格离散。该方法设置简单、计算效率高，可用于螺栓强度的校核计算、螺栓疲劳破损的相关问题的研究，适用于螺栓组连接的装配体力学性能的研究，因此MPC法建模更适用于螺栓组工程化建模。

图6 MPC法有限元模型Fig.6 Finite element model of MPC method

2.4 计算结果及分析

对比3种建模方法，其单元类型、材料参数和边界条件都相同，在螺栓上施加64.8 kN的螺栓预紧力，上表面施加-5 MPa的压力载荷，约束下板底面。螺头与上板、上下板之间的接触都为摩擦接触，摩擦系数为0.1。提取3种模型在预紧力和外载荷作用下的应力云图如图7所示。

图7 应力云图Fig.7 Stress nephogram

从图7中可以看出，三者的应力分布规律及大小基本吻合，线性螺纹模型和MPC法模型与真实螺纹模型最大应力误差小于6%。图7(b)与图7(a)的应力分布更接近，说明采用线性螺纹建模可以很好地替代真实螺纹，这种方法适用于对螺纹位置性能的研究。图7(c)应力云图螺栓杆位置、螺头位置和接触面位置的应力分布与真实螺纹应力分布吻合，只是在螺纹连接处有所区别，因此MPC法适用于风电轴承的螺栓组力学性能的研究。

提取的3种模型的螺栓等效应力、最大拉伸应力与理论结果如表1所示。

表1 结果比对分析表Table 1 Comparison and analysis of the results

由表1中可以看出，真实螺纹模型、线性螺纹模型和MPC法模型与VDI2230标准计算出的螺栓工作应力的误差分别为4.8%、4.5%、4.3%，最大螺栓力的误差均为1.5%。最大变形量MPC法模型与真实螺纹模型误差为12%，小于15%，在允许误差范围内。综合以上几组误差，MPC法工作应力与最大螺栓力误差较小，变形量在允许范围内，因此通过计算时间、计算结果收敛性和建模的复杂程度，采用MPC建模方法替代真实螺纹模型的建模方法，该方法适用螺栓组仿真计算。

3 变桨轴承螺栓连接的力学性能分析

3.1 螺栓模型

以某3.4MW级风电机组叶片与变桨轴承内圈最危险的单螺栓模型为例，如图8所示，通过M39高强度螺栓连接。材料的弹性模量E=200 GPa，泊松比μ=0.3，摩擦系数f=0.15[12]。网格尺寸为5 mm，边界条件两侧采用对称约束，叶片顶部固定约束。

图8 单螺栓模型Fig.8 Single bolt model

由实际载荷谱获取一组最大组合力，其中轴向力为438.1 kN、径向力为524.5 kN、倾覆力矩为17 780 kN·m，依据转换公式(23)[13]，并由变桨轴承实际多体有限元模型得到滚道最大接触载荷值FA=127 kN，将最大接触载荷FA以接触角为45°方向通过建立的滚动体接触面施FA在子模型内圈表面。

(23)

3.2 预紧力大小对结果的影响

对单螺栓模型分别进行3种工况计算。模型空载，仅受预紧力作用下的连接性能，改变预紧力大小，查看应力分布情况，结果如图9所示。由图9中可以看出，应力分布规律与上述理论模型所得的应力分布规律一致，且应力随预紧力的增加成正比增长。因此，在螺栓达到屈服应力之前且不超屈服极限的80%，预紧力应尽可能大，这样才能保证连接性能的可靠性。

图9 受预紧力作用等效应力云图Fig.9 Equivalent stress nephogram under preload

预紧力与下接触载荷共同作用工况，在接触载荷恒定127 kN的情况下，改变预紧力的大小，考察其应力分布云图，结果如图10所示。由图10中可以发现，最大应力发生在滚动体接触区域，且在预紧力有效范围内增加对于最大等效应力的取值影响不大。

图10 等效应力云图Fig.10 Equivalent force nephogram

预紧力和上接触载荷共同作用工况，由于转盘轴承受到周期性的工作载荷，因此滚动体会对上下接触面产生周期性接触，在接触载荷为127 kN、预紧力为550 kN的条件下，分别提取3种载荷下沿Z轴的变形云图，结果如图11所示。由图11中可以看出，只受预紧力作用时最大变形为0.31 mm，受预紧力和下接触载荷时最大变形为0.43 mm，受预紧力和上接触载荷作用时最大变形为0.27 mm。从图11中还可以看出，随着载荷的周期性变化，变形的大小和方向也会随之改变。

图11 Z轴变形云图Fig.11 Z-axis deformation nephogram

4 结论

(1)基于VDI2230标准的螺栓连接理论可以准确地计算出螺栓的力学性能，对有限元的分析结果提供理论依据。

(2)提出一种MPC法螺栓连接的有效建模方法，验证了该方法的适用性，且能够获得具有理论支撑的准确结果，误差控制在5%内。该方法计算过程简单、效率高，对风电变桨轴承的螺栓连接设计及计算分析具有指导意义。

(3)在不关心螺纹细节处力学性能的螺栓组连接件中，通过施加不同工况下的载荷就可以得出相应工况下的应力应变状态，避免手工计算的复杂、误差等问题。而对于研究螺纹处力学性能状态的问题，给出一种截面螺纹建模方法，该方法只需要给出截面螺纹参数就可以得到相应的螺纹细节处应力状态，且与真实螺纹模型吻合。

综上所述，提出的3种方法区分了变桨轴承螺栓连接研究侧重点。MPC法计算准确、计算时间少，可应用工程中风电变桨轴承螺栓连接的力学强度计算及校核，避免了理论计算的复杂性和误差。