振动的带电粒子、磁场中的金属丝和轻杆——国际物理奥赛IdPhO2020理论第一题解析

苏 俊 宋 峰

(1.华东师范大学教师教育学院 200062；2.江苏省海安高级中学 226600；3.南开大学物理科学学院 300071)

问题1解析：

建立直角坐标系，坐标原点位于立方体中心，三个坐标轴平行于立方体边线。设粒子坐标为（x，y，z），其中x ＜＜a，y ＜＜a，z ＜＜a。

为了分析粒子的受力情况，我们将边长为a的立方体分成一个长方体和三个小块，长方体的边长为(a-2x)×(a-2y)×(a-2z)，三个小块的厚度分别为2x、2y、2z的方块。如图1所示。

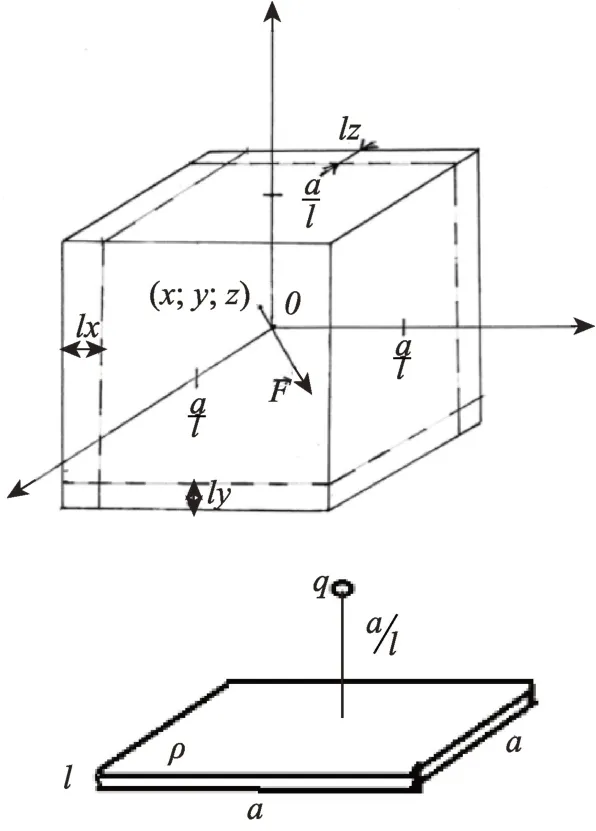
图1

当粒子位于长方体中心处不受力，我们来分析带电量为q的粒子与厚度为h、长度为a的均匀带电小块之间的作用力。小块的电荷密度为ρ，粒子到小块中心的垂直距离为a/2。根据对称性和高斯定理，粒子电通量为：

式中ε0为真空介电常数。

带电粒子所受的作用力为：

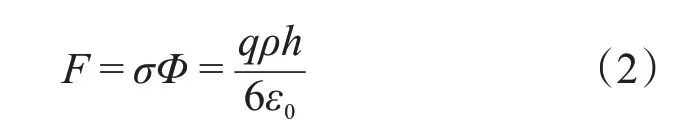
其中电荷面密度为σ=ρh。

三个小块对粒子的作用力分别为

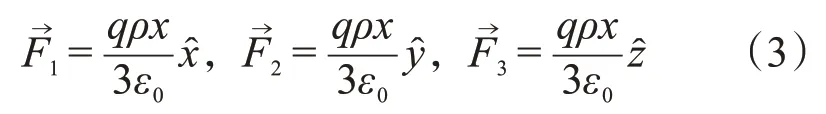
则回复力为：

其中为位置矢量。

由牛顿第二定律，粒子的运动方程为：

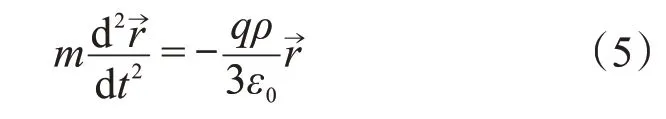
m为粒子的质量，则回复系数：

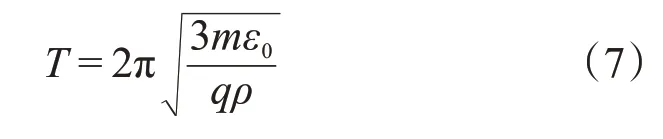
解析：本题要求出带电粒子的振动周期，通过高斯定理求出静电力，而回复力来源于静电力，给出回复力与位移的线性关系，得到线性系数即回复系数k，则可以得到周期T。

问题2解析：

方法一：

我们考虑线圈上的一小段dl，其受到的安培

力为：

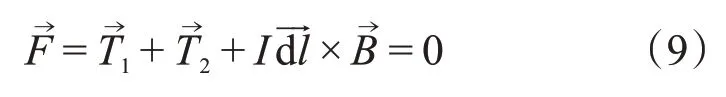
因此，在两段线圈上张力均为常数，又由于对称性，这两个常数相等，所以整根绳子上张力大小均为常数T。

对于离线圈顶部悬挂点距离为l(线元到悬挂点沿绳的长度)的线元，设其切向矢量为，则可以将(9)式写为：

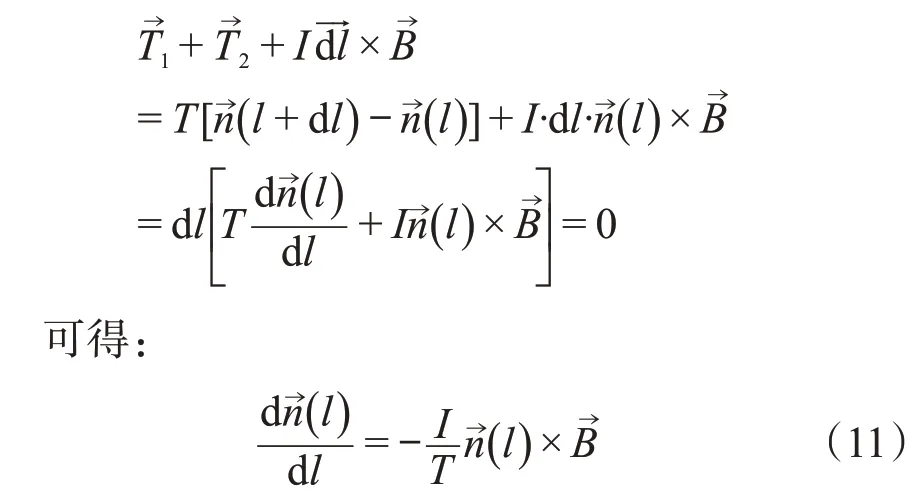
由上式可得：

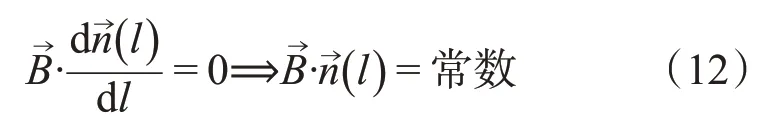
即线圈上每一点的切向向量n→都和磁场B→的夹角相同。在水平面上随着l以匀速旋转，因此我们可以认为线圈的两个部分(最高点到最低点)都缠绕着一个圆柱体，并且与磁场保持着一个固定的角度α。为了找到此圆柱体的半径，我们将上述表达式投影到水平面：

在线圈的最低点悬挂着重物，在此点三力平衡：两个张力（来自线圈的两部分）以及重物对线圈的拉力（源自于重力，竖直方向）。因此这三个力应该位于同一个竖直平面，线圈的两部分缠绕的圆柱半径相同。线圈形状如图2，线圈上每一点切线方向与竖直方向(即磁场方向)夹角均为α。线圈分为两段，每一段都是绕着圆柱的螺旋线。

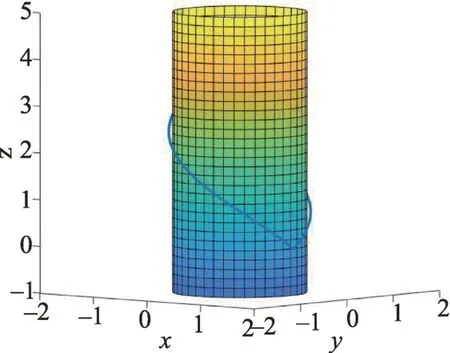
图2

可以算出线圈的半周长：

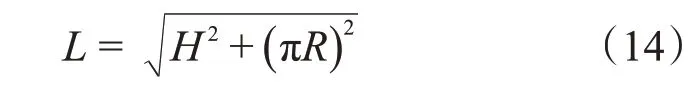
式中，H为最低点到最高点高度差，R是圆柱体的半径。

因此：

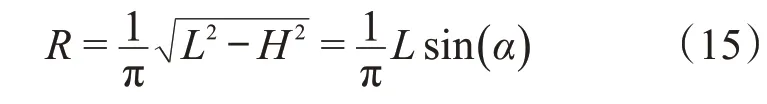
可得到线圈中的张力为：

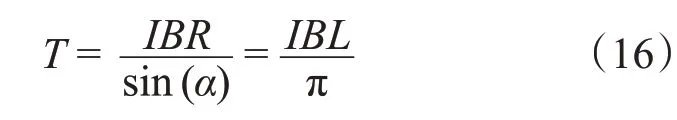
于是，我们得到悬挂物的重量为：

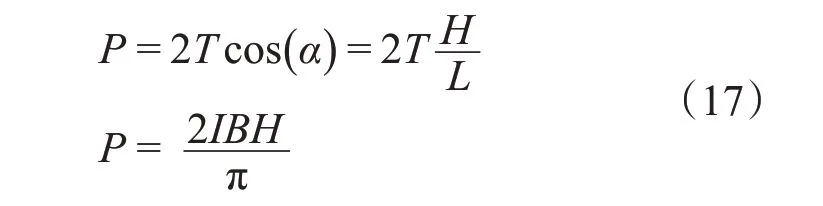
方法二：

稳定的平衡对应于势能的最低点。该题总的势能是重力势能和电流在磁场中能量之和。我们用S表示线圈在水平面的投影面积，则有：

Ep取决于两个变量：H和S。注意到在不改变H的情况下可以改变线圈在水平面的投影面积。所以，在H不变的情况下增加S从而减小势能。势能的最小值对应于S的最大化（在水平平面的周长不变的情况下），即线圈在水平面的投影是一个圆。

而当投影确定之后，H会在线圈与竖直轴成一个固定夹角时达到最大值。因此线圈的形状是柱面上的螺旋线。

则：

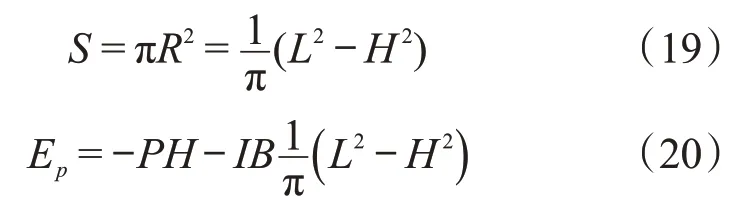
势能的极小值条件是：

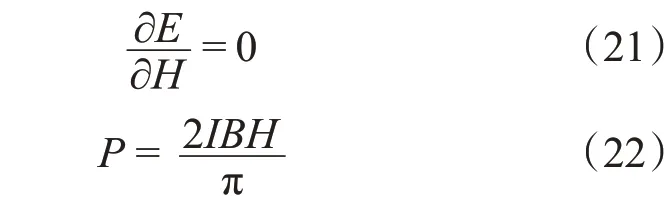
讨论：本题可以从受力的角度进行进行，物理过程比较清晰，但是矢量计算比较繁琐。另外也可以能量的角度分析，方法简洁，但是物理过程没有受力分析直观。读者可以从两个角度来理解该问题。

问题3解析：

方法一：

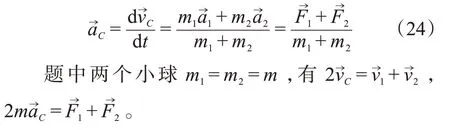
对于两个球体、轻质杆所构成的系统，有3个外力，洛伦兹力、重力与悬挂装置对系统的拉力，下面证明悬挂装置对系统的拉力大小恰好为两个小球的重力大小。注意到杆的质量为0，即杆的加速度为0。分析杆的受力，其受两个小球对杆的作用力和悬挂装置对杆的拉力。两个小球受到的重力相同，为，洛伦兹力的大小相同，方向相反以及杆对小球的作用力两个小球的向心力等大反向，从而有：

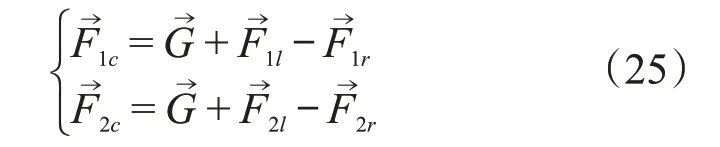
系统所受的合外力为0，从而给出两个球体质心的运动方程为：

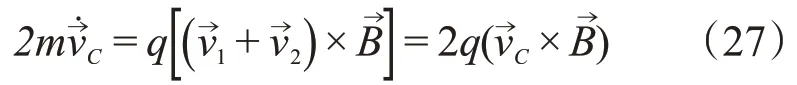
式中为质心(杆的中点)的运动速度，和分别是两个小球的运动速度。在运动开始时，质心速度vC=0，在之后的运动中vC也是0。以质心为转动中心的方程为：

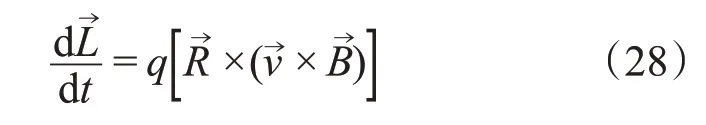
题中要求是沿着z轴的，那么，式子中的z是小球的z轴坐标。考虑转动方程的z轴分量：

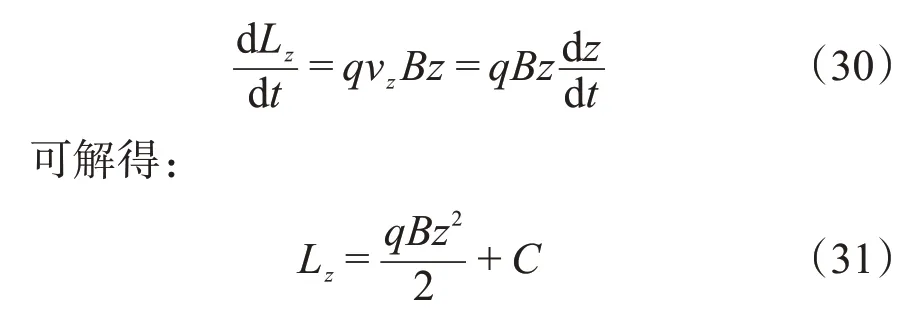
由初始条件z=0 和Lz=0，可以解出C=0。

当小球的角动量在z轴上投影到达最大值时，小球速度的z分量为vz=z˙=0，此时系统的角动量L=Lz=mur，其中r是小球到z轴的距离，u是小球的速度。另外，小球是在一个以杆的中心为球心的球面上运动，满足r2+z2=R2。洛伦兹力和杆对小球的作用力不做功，这表明该系统的动能不变，结合质心速度0 的条件，可以得知u=v。我们可以得到小球角动量的z分量代入（31）式，得到一个关于zmax的一元四次方程：

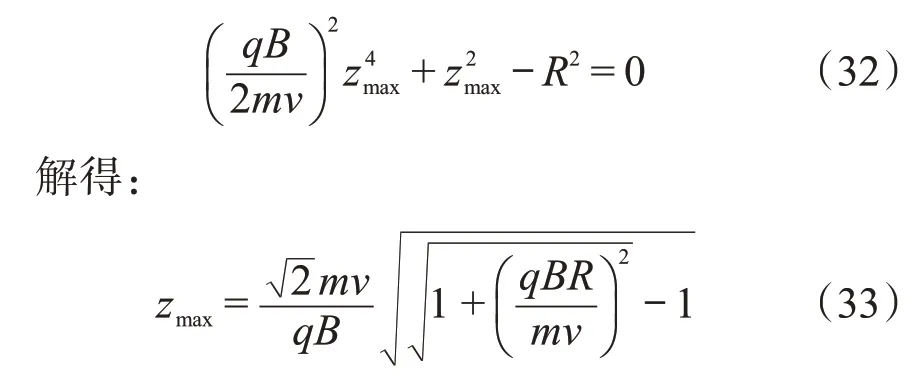
考虑3 个正交的单位矢量，第1 个沿着小球的速度方向，第2个沿着小球到杆的中心方向，第3个则垂直于前两个单位矢量。在先前的分析中可知v=const，所以a1=0。沿着第2个单位的加速度是小球的向心加速度a2=v2/R。牛顿第二定律在第3个单位矢量的方向为最终得到：

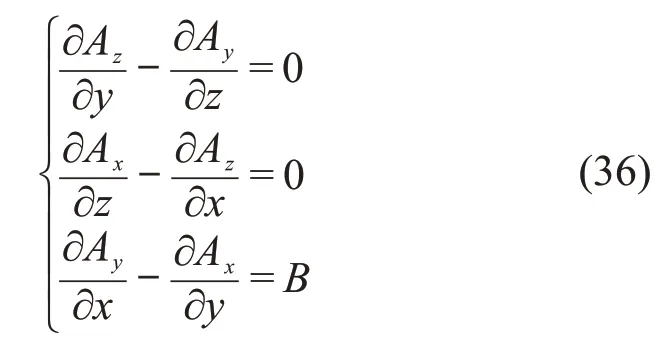
选取磁矢势的解需要一些技巧，观察上述方程组，可以发现，Az=0，且Ax、Ay与z无关，可以满足（36）式前两个方程，整理成表达式为：

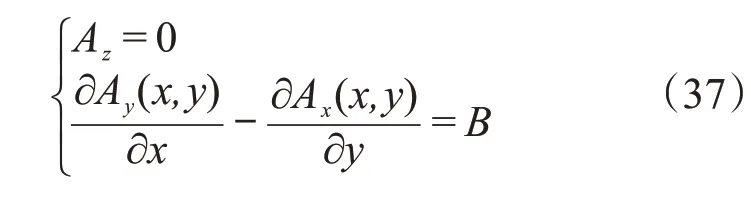
可以看出Ay=Bx，Ax=0 或Ax=-By，Ay=0等都是方程的解，为了方便后续求解，取如下形式：

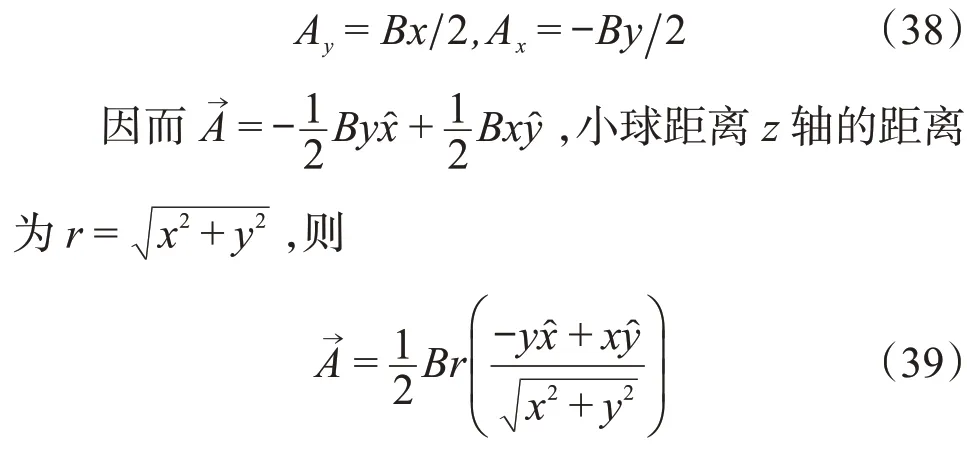
其中括号内为单位矢量，定义为。从磁矢势表达式，可以看出该磁矢势是一个环绕着z轴的环形矢量场，具有圆柱对称性，则柱坐标系下对应的广义动量的分量应该是守恒的。柱坐标系的三个自由变量为(r，θ，z)，需要注意的是守恒的广义动量分量是由环绕着z轴的场产生的，对应的广义动量是由θ产生的角动量：

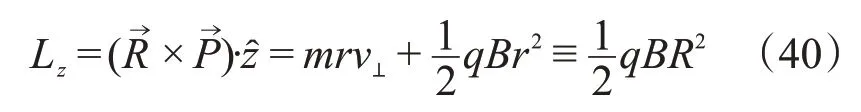
上式v⊥是垂直于z轴的速度分量，当小球在z轴的角动量投影达到最大时vz=˙=0，有v⊥=v，得到一个关于的方程：

讨论：本题可以从粒子的角动量角度求解，这也是大家使用的常规方法。另外也可以通过广义动量求解该问题，对物理知识要求较高，有兴趣的同学可以查阅电磁学相关知识作进一步学习。