自适应噪声整体经验模态分解法在CORS站数据处理中的应用

李 婷

(浙江省国土勘测规划有限公司 浙江杭州 310030)

作为重要的空间数据基础设施，连续运行参考站(CORS)为社会各行业提供稳定的位置信息服务。目前，国内外许多国家和地区已经开展或建成了CORS系统，建立全天候、全覆盖、高精度和实时动态定位的卫星导航系统是国际大地测量的一个发展趋势。对CORS站进行观测时，环境因素的影响使得其观测数据在高程方向存在较大噪声。因此，通过剔除观测数据中的噪声，获取CORS站高程方向真实值具有重要的意义。

对于CORS站高程时间序列的非线性、非平稳信号，通常利用事先给定的周期函数模型拟合趋势项和周期项去除非平稳性，但是，这种方法得到的分析结果不准确，甚至会偏离序列真实的运动情况。近些年来，整体经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法被广泛应用到时间序列分析中，经EEMD法分解后的信号可以得到若干含有特征时间尺度的本征模态函数(Intrinsic Mode Function，IMF)分量，从而对信号进行多分辨率分析[1]。吉长东等[2]将EEMD方法应用到CORS站时间序列分析中，有效地改善了信号分解过程中产生的模态分解问题，但还会存在整体平均不能完全消除噪声的影响。本文引入一种新的噪声自适应整体经验模态分解(Empirical Mode Decomposition with Adaptive Noise，EEMDAN)方法，与EEMD方法不同的是，EEMDAN方法在经验模态分解处理时添加白噪声分解的模态分量，可以改进CORS站高程时间序列信号分解的模态混叠。最后利用某市高程CORS站点数据，验证EEMDAN方法处理CORS站高程时间序列的有效性。

1 EEMD及EEMDAN

1.1 EEMD

EEMD可以对待处理信号的极大值特征尺度进行信号分解，通过不断筛选，将待分解信号分解为频率各不相同的IMF，根据频率的不同来反映周期长度，体现了对信号多分辨率分析的滤波过程。EEMD方法的滤波过程是通过对信号进行EEMD分解产生IMF分量，根据IMF分量特征，构造时空滤波器。

分解后的IMF可以反映信号不同范围的特征尺度，通过特征可以对信号进行滤波。以往是通过傅里叶变换在频域上实现滤波，其缺点是会在频域产生谐波信号，很难将信号的频谱有效分离。

对监测体进行变形监测采集的GNSS数据，噪声与有用信号的时频特性是有区别的。GNSS时间序列中通常存在由于多路径影响产生的频率低于结构特性的低频噪声，也会存在频率高于结构特性的高频噪声。结合GNSS的多路径特点，对GNSS监测数据经EEMD分解产生的不同频率特征相关性进行分析，从而消除多路径误差对观测信号的影响。

1.2 EEMDAN

EEMDAN是对EEMD方法的改进。与EEMD分解所有 IMF分量进行整体平均不同的是，EEMDAN分解得到第一阶分量后即进行整体平均，并将第一阶整体平均IMF剔除后得到除第一阶整体平均IMF的剩余分量，再对剩余分量进行整体平均，得到第二阶、第三阶直至最后一阶IMF分量[3]。EEMDAN滤波过程的主要步骤如下[4]：

第一步：将白噪声添加到信号中做经验模态分解(Empirical Mode Decomposition，EMD)，对分解的IMF分量进行平均化处理，获取第一阶IMF分量。

第二步：剔除第一阶分量后，得到剩余信号，再分解后得到含有噪声的模态分量集；在剩余信号中加入该模态分量集，组合成分解信号，继续进行EMD分解，得到第二阶分量。

第三步：剔除第二阶分量后，重复第二步，直至剔除最后一阶模态分量后得到剩余信号。

EEMDAN利用白噪声频谱分布均匀这一特性，对CORS站点的时间序列进行投影，以达到消除由分解带来的模态混叠。EEMDAN可以将上一次分解后的剩余信号作为下一次分解信号，减小了重构误差和整体平均噪声在没有消除的情况下对信号分解造成的影响。

2 CORS站点时间序列分解评价标准

对CORS站点时间序列进行分解，可以通过两个指标评价其分解效果，一是分解后的IMF分量是否存在模态混叠；二是参考正交性指标(Orthogona-lity Index，IO)，分解精度随着IO的减小而提高。IO可表示为

(1)

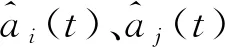
将CORS站时间序列分解为一系列不同的IMF分量，若将Tj和CMSEj定义为第j个IMF分量的平均周期与能量密度，则可以通过参考分量的能量密度与平均周期的乘积得到信号与噪声的临界位置(const值)，通过判别临界位置来剔除包含噪声的分量，完成对信号的重构。通过计算重构后的相关系数R和均方根误差(RMSE)来量化重构效果。相关系数R越大，重构效果就越好；RMSE值越小，重构信号的精度与质量越高[5-7]。

R和RMSE可分别表示为

(2)

(3)

3 试验分析

本文选取某市CORS站BTRD站点2016年1月1日—2019年12月31日的GNSS高程观测数据为试验数据，对高程观测数据进行均值化处理，图1所示为高程观测数据时间序列。

图1 BTRD站点2016—2019年高程方向上时间序列

3.1 分解精度分析

为了便于对比，将原始信号标准差与噪声的比值设置为10，经EEMD和EEMDAN两种方法分解得到部分低频IMF分量如图2所示(实线表示的是EEMD分解结果，虚线表示的是EEMDAN分解结果)。

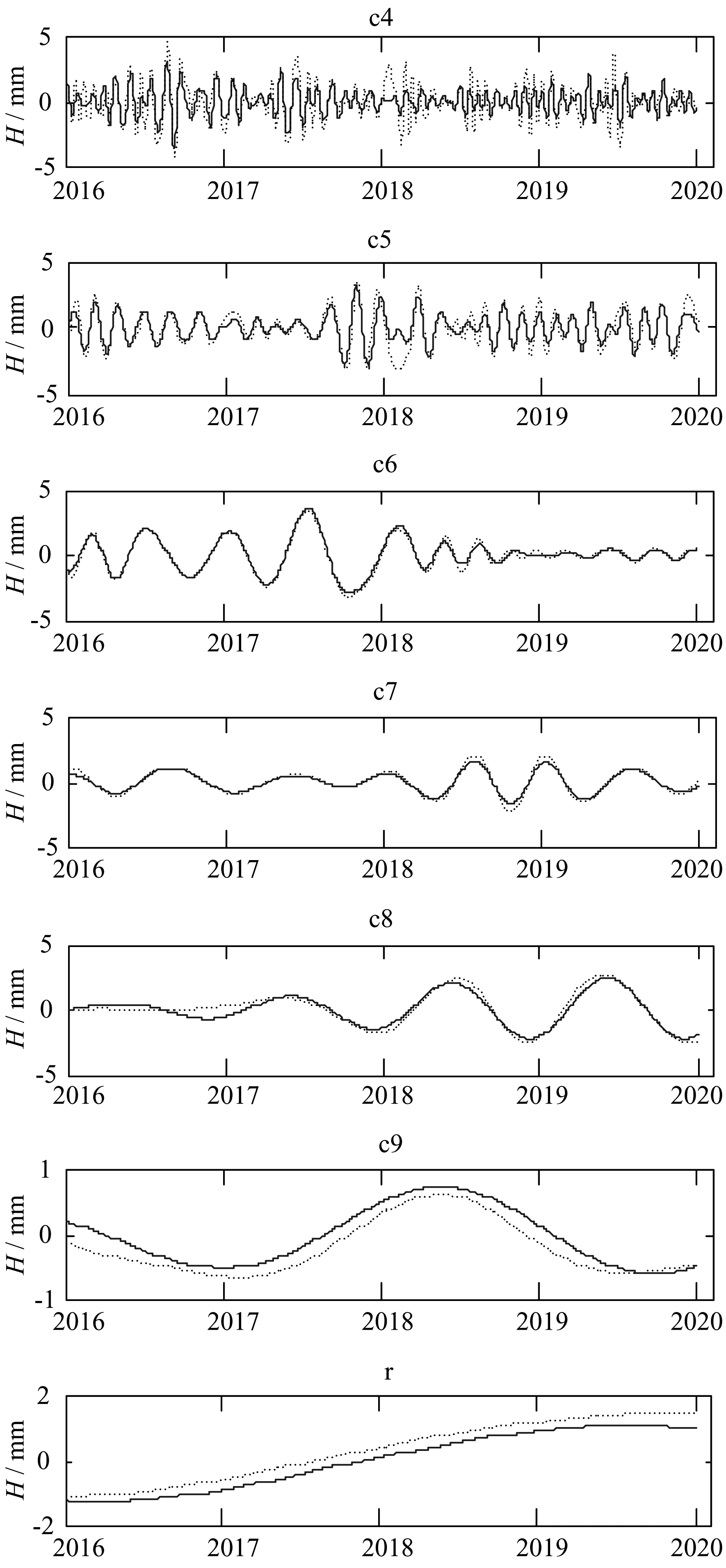
图2 BTRD站点高程时间序列分解得到的部分IMF分量

本文使用IMF分量的方差贡献率获取CORS站点时间序列运动的周期形式。IMF分量在整个时间序列中的比重可以用该分量的方差贡献率反映，时间序列中的主要周期运动贡献项由方差贡献率高的IMF分量组成。BRTD站点高程时间序列经EEMD和EEMDAN两种方法分解的低频分量的方差贡献率如表1所示。

表1 不同IMF分量的方差贡献率 单位:%Tab.1 Variance Contribution Rate in Different IMF Components 方法c4c5c6c7c8c9EEMD21.428.64.11.25.70.8EEMDAN24.826.33.93.10.91.4

由表1可知，BRTD站点高程时间序列经EEMD分解后，IMFc4与IMFc5方差贡献率所占比重最高，分别为21.4%与28.6%，为时间序列中的主要周期贡献项。BRTD站点高程时间序列经EEMDAN分解后，同样是IMFc4与IMFc5的方差贡献率占比最高，分别为24.8%与26.3%。

对于BRTD站点高程时间序列来说，可以通过IMFc4与IMFc5两个分量表现出周期形式。为了评价EEMD和EEMDAN两种方法的分解精度，计算方差贡献率较高的IMF分量之间的正交指数，结果如表2所示。

由表2可知，取200次整体平均的分解精度比取100次整体平均的分解精度低，也符合文献[8]中的推荐值。通过计算EEMD和EEMDAN两种方法分解后的IMF分量的IO值，可知EEMDAN方法的分解精度比EEMD方法的分解精度提高了53.7%。

表2 方差贡献率较高的IMF分量之间的正交指数Tab.2 Orthogonal Index of IMF Components in Higher Variance Contribution Rate方法N=100N=200EEMD0.054 10.068 7EEMDAN0.035 20.041 6

3.2 重构信号分析

BRTD站点高程时间序列经EEMD和EEMDAN两种分解方法分解后得到不同频率的IMF分量，其中IMFc1～IMFc3是高频分量。为了有效剔除噪声并重构得到有用的信号，通过IMF分量的能量密度与平均周期的乘积指标来识别和剔除噪声，其计算结果见表3。

表3 BRTD站点分解分量的能量密度与平均周期乘积Tab.3 Product of Energy Density and Average Period of Decomposition Component of BRTD Station方 法指 标c1c2c3c4c5c6c7EEMDT/d3.4067.25814.32631.43360.221177.274384.214CMSE/(cm2/d)0.3570.2140.1550.1640.0980.2860.179T×CMSE/cm21.2161.5532.2205.1555.90250.70068.774EEMDANT/d3.3577.16615.82328.16344.581159.548181.532CMSE/(cm2/d)0.2440.1950.0970.1470.1260.3270.218T×CMSE/cm20.8191.3971.5354.1405.61752.17239.574

陈仁祥等[9]根据CMSE值是否发生明显变化来判断信号与噪声的临界点，但是，这种判别方式在进行噪声剔除时，会将双月与近似月的分量剔除。故本文引入const值作为噪声与信号的判别标准[10-12]。

对于BRTD站高程时间序列，经EEMDAN处理后的前3个分量的const均值为1.250，前3个分量const值与均值的最大偏差不超过34.5%，而IMFc4的const值与均值的偏差超过2倍；经EEMD处理后的前3个分量的const均值为1.663，前3个分量const值与均值的最大偏差不超过36.8%，最小偏差为7.1%，而IMFc4的const值与均值的偏差超过2倍。因此，EEMD与EEMDAN分解得到的结果相同。

const值对噪声与信号的区别判别指标主要是针对信号中高斯白噪声，对有色噪声的处理效果并不理想。通过噪声识别对提取的信号进行重构，其结果如图3所示，重构信号的均方根误差与相关系数见表4。

表4 信号重构后的均方根误差与相关系数Tab.4 RMSE and Correlation Coefficient after Signal Reconstruction方法RMSE/mm相关系数/%EEMD1.57596.7EEMDAN1.29698.8

由图3与表4可知，经EEMD与EEMDAN两种方法重构后的时间序列均能有效提取信号中的有用信息，但是经EEMDAN处理后的信号均方根误差比经EEMD处理后的均方根误差减少21.5%，相关系数增加2.1%，表明经EEMDAN剔除噪声，重构信号的结果要比经EEMD方法得到的结果更好。

图3 两种方法重构后时间序列

这是因为EEMDAN处理CORS站高程时间序列时，较好地利用了白噪声频谱均匀分布的特性，使信号能够在遍布整个时频空间且分布一致的白噪声背景上，按照合适的尺度进行投影，以此来削弱分解产生的模态混叠。

4 结 语

以EEMD为基础的EENDAN方法改进了对整体平均的处理，通过计算分量能量密度与平均周期的乘积、均方根误差、相关系数和正交性指标的值，验证了EEMDAN方法的分解精度与重构后信号的效果都要比EEMD方法好。

基于信号特有的运动特征，EEMDAN方法可以将原始信号的有用信息提取出来，为CORS站点时间序列的处理提供有益的参考。但是本文对于如何剔除信号中有色噪声没有做进一步的研究。