基于谱分析模型的GPS卫星钟差预报特性分析
马 旺 王志远 谭开文
(61365部队)
从卫星自主导航的先验信息供应、精密动态实时单点定位需求、钟差参数优化等角度来看,卫星导航定位系统的钟差预报(星载原子钟)作用极为明显[1]。近年来,各国理论界纷纷强化卫星钟差预报技术探索,诸如基于灰色系统模型、二次多项式(Quadratic Polynomial,QP)模型、时间序列模型、线性模型、卡尔曼滤波模型和神经网络模型[1-5]等类型各异的卫星钟差预报模型陆续被提出并予以验证。这些模型在进行钟差预报时各有特点[6],而应用最为普遍的钟差预报模型为QP模型,其优势包括参数涵义清晰和建模简单等。GPS的导航电文钟差预报也是采用该模型。但从预报实践来看,GPS卫星钟差的周期特征被二次多项式模型忽略,而导致该模型钟差预报精度较低。频谱分析是一种将复杂信号分解为较简单信号的技术。许多物理信号均可以表示为许多不同频率简单信号的和,找出一个信号在不同频率下的信息(如振幅、功率、强度或相位等)的做法即为频谱分析。为提高卫星钟差预报精度,本文以卫星钟差周期特征为切入点,借鉴频谱分析方法,结合QP模型给出了一种钟差预报的谱分析(Spectrum Analysis,SA)模型,并使用GPS卫星钟差数据进行预报验证,根据验证结果进行GPS卫星钟差预报特性分析。
1 卫星钟差预报的谱分析模型
星载原子钟是导航卫星上的一种基本设备,通常有铯钟(Cs.clock)、铷钟(Rb.clock)两类。因QP模型同时具备用于卫星钟时频域稳定性描述的3种参数(频漂、频率、相位),可大体表现出星载原子钟的物理属性。另外,从实践角度来看,卫星钟周期性波动特征不应被忽视,只有高度重视,才能更加准确清晰地体现出星载原子钟的特征[7]。如果时间序列存在周期性波动特征,一般需要数据序列的显著周期项通过频谱分析法检索出来,这样数据建模精度才能有效提升,预报准确性也能不断提高。GPS卫星钟差数据谱分析模型[8]为
(1)
式中:Li为ti时刻卫星钟差;t0为参考时刻;ti为历元时刻;a0为参考时刻t0钟差;a1为参考时刻t0钟速;a2为参考时刻t0钟漂;p为主要周期函数的个数,基于频谱分析策略确定,大小由功率谱确定;Ak为对应周期项振幅;fk为对应周期项频率,基于频谱分析策略确定;φk为对应周期项相位;k=1,2,3,…,p;Δi为观测误差。
从式(1)可以看出,钟差预报的SA模型由QP部分和1组周期函数组成。具体实现过程:基于QP模型拟合已知钟差数据,获得拟合残差;将拟合残差从时域向频域变换,在变换过程中,拟合残差会进行数个简单的正(余)弦信号分解、叠加,这些正(余)弦信号存在频率差异,其功率谱就能说明不同正(余)弦信号的频率。原始信号中频率信号功能与功率谱之间具有正相关性,p与fk通常基于最大功率谱量级来确定。在确定了p、fk的条件下进行模型参数估计。为了便于求解,设:
(2)
进而得到(1)式的线性形式:
(3)
其矩阵表达式为
L=AX+Δ
(4)
式中:L为由n维已知钟差数据构成的观测向量;Δ为n维误差向量;X为2p+3维待估参数向量,X=[a0a1a2b1c1… …bkck… …bpcp]T;A为n×(2p+3)维系数矩阵。
根据最小二乘原理,可得参数X的估值:

(5)
根据求得参数使用以下谱分析模型进行钟差预报。
(6)
式中:An+j为系数矩阵。
2 预报试验及其结果分析
2.1 预报试验
试验数据采用基于GPS卫星定位系统900 s采样间隔的最终精密钟差数据(2013年6月27日—9月14日,共计80 d),BLOCK ⅡF铷钟、BLOCK ⅡF铯钟、BLOCK ⅡR和BLOCK ⅡR-M铷钟、BLOCK ⅡA铷钟、BLOCK ⅡA铯钟均为选定时段星载原子钟。预报试验是基于这80 d时间段中一颗卫星的完整数据进行的,其中PRN01、PRN10、PRN22、PRN24、PRN29、PRN32为本试验预报的 6颗卫星。
预报测试参数确定:统计量为极差(Range)与均方根误差 (Root Mean Square,RMS),参考真值为IGS(International GNSS Service)精密钟差值。均方根误差求解方程:

(7)
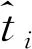
基于2013年7月3日1 d的钟差数据分别拟合并建立QP模型和SA模型,进行12 h、24 h、1周、半个月、1个月和2个月的钟差预报,其中,12 h和24 h预报是短期预报,1周和半个月预报是中期预报,1个月和2个月预报是长期预报。
2.2 试验结果分析
首先,以PRN01卫星的建模分析过程为例来说明SA模型的实现过程。图1是PRN01卫星使用QP模型对已知建模钟差数据进行拟合后的拟合残差图和残差能量频谱图。
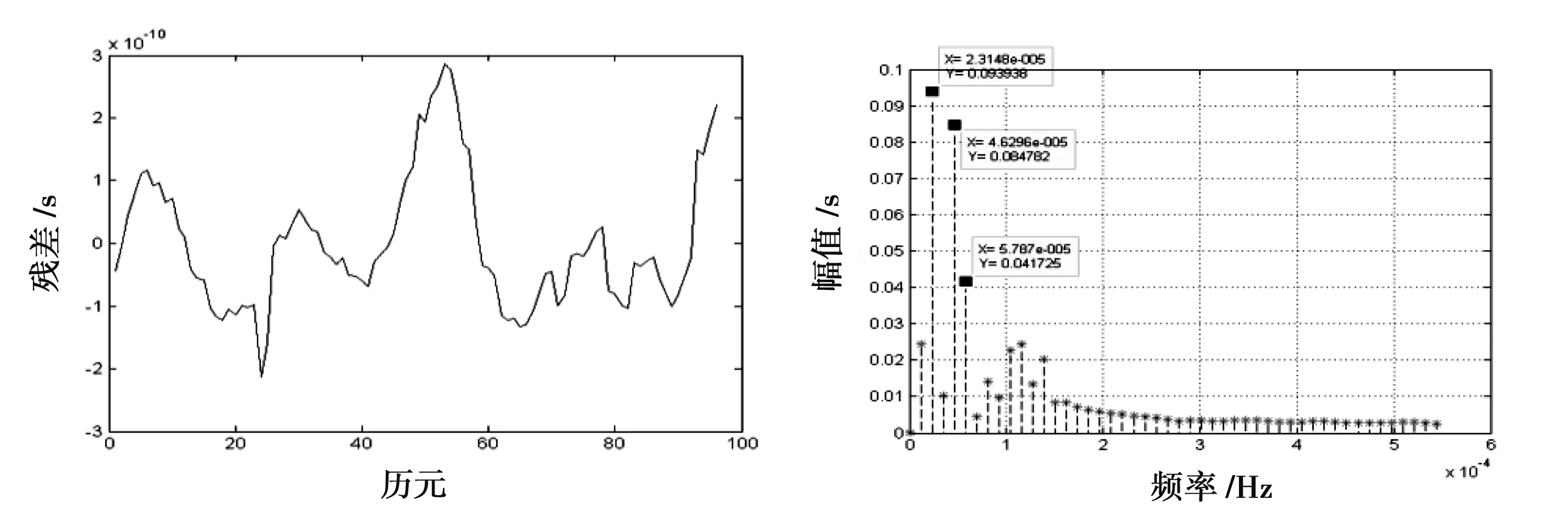
图1 PRN01卫星二次多项式拟合后的残差和去噪后拟合残差的谱分析图
分析能量频谱图,幅值较大点如果出现在3个不同部位,那么周期函数(谱分析模型中)就能顺利确定。因此可得PRN01卫星的参数,即p= 3,f1= 2.314 8×10-5HZ,f2= 4.659 6×10-5HZ,f3= 5.787×10-5HZ。同理,可确定剩余卫星相应的参数。考虑文章的篇幅,本文只给出PRN01卫星使用QP模型和SA模型进行1 d钟差预报的预报结果和预报误差图(图2),基于QP模型和SA模型得到的6颗卫星的钟差预报结果统计见表1。需要说明的是,从图2可以看出,使用QP模型和SA模型进行1 d 钟差预报的预报结果与IGS发布的值符合性很好。
根据图2和表1的预报结果,对谱分析模型与QP模型的钟差预报特征进行分析。
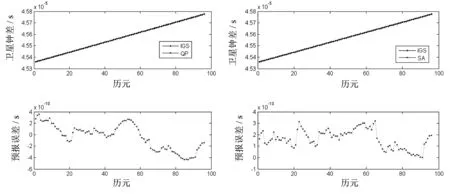
图2 QP模型和SA模型的预报结果与预报误差
首先,对于短期预报(24小时内),QP模型在拟合事后钟差数据前提下可以反映钟差变化规律,预报结果较准确,精度可达到亚纳秒级;从预报稳定性来看,铯钟最多有几十纳秒,而铷钟则最多只有数纳秒。对于中长期预报,预报结果偏差与预报时间增加具有正相关性,时间越长,偏差越明显,模型预报结果的稳定性和精度无论是铯钟还是铷钟都迅速降低。
其次,SA模型的钟差预报结果通常会优于QP模型的钟差预报结果,主要是因为SA模型可以高效拟合星载原子钟周期项,从而在一定程度上提高了预报结果的稳定性和精度。但是从长期预报实践来看,如果延长预报的时间,受到二次多项式主项的影响,谱分析模型的预报偏差会明显加大。
最后,根据表1的统计结果(各星末列),SA模型、QP模型在钟差预报环节,如采用的星载原子钟种类不一样,钟差预报结果的稳定性和精度也会不同。
本研究只是对GPS系统的钟差预报特性进行了分析,下一步还可分析SA模型在北斗导航系统等其他卫星导航系统钟差预报的特性。

表1 QP模型和SA模型的预报结果单位:nsTab.1 Prediction Results of QP model and SA Model 卫星类型统计量预报0.5 d预报1 d预报7 d预报15 d预报30 d预报60 d平均值QP模型PRN01(ⅡF Rb)PRN10(ⅡA Cs)PRN22(ⅡR Rb)PRN24(ⅡF Cs)PRN29(ⅡR-M Rb)PRN32(ⅡA Rb)平均值RMS0.1420.22308.725039.044277.4561 837.746360.555Range0.4800.75119.387089.026733.8484 483.904887.906RMS3.1074.330112.712562.7532 328.2619 295.9132 051.179Range7.75012.050267.9851291.6295 230.2162 0788.2074 599.639RMS3.19307.105198.851787.8902 715.12110 099.9252 302.013Range5.16613.603433.8511 650.9495 917.43422 261.7225 047.120RMS7.86518.051370.0261 622.8956 303.94524 859.6045 530.398Range12.95135.261815.9583 573.47614 029.55055 396.61512 310.635RMS0.65001.546024.40570.605102.434214.58669.037Range1.36503.149049.915112.589167.356371.259117.605RMS2.04105.327145.675631.0212 441.2549 487.5852 118.816Range3.43810.257315.3831 399.5625 402.48421 045.9664 696.181RMS2.83306.098143.400619.0352 361.4129 299.2272 072.001Range5.19312.517317.0801 352.8725 246.81520 724.6124 609.848SA模型PRN01(ⅡF Rb)PRN10(ⅡA Cs)PRN22(ⅡR Rb)PRN24(ⅡF Cs)PRN29(ⅡR-M Rb)PRN32(ⅡA Rb)平均值RMS0.1870.1812.60912.881178.6031 442.339272.800Range0.2300.3206.31131.503509.0583 595.898690.553RMS4.7773.481216.8481 003.2004 024.59315 950.9753 533.979Range9.5769.576486.0412 253.5148 985.10335 600.7927 890.767RMS1.7664.783152.619597.7531 991.4677 277.8721 671.043Range3.74510.340335.6701 235.1224 316.72515 985.3073 647.818RMS7.22616.716340.9021 501.1535 837.36323 033.4795 122.807Range12.28432.516752.9333 305.80912 995.40351 331.66011 405.101RMS1.1561.84051.641251.2301 137.4384 618.9701 010.379Range2.2423.450114.375591.9582 562.26110 375.7722 275.010RMS2.1803.04331.088107.036385.4401 573.179350.327Range3.6574.63263.993219.556859.0603 570.501786.900RMS2.8825.007132.618578.8762 259.1518 982.8021 993.556Range5.28910.139293.2191 272.9115 037.93620 076.6564 449.358
3 结 语
从系统时间同步保持、钟差参数优势化等实践来看,卫星钟差预报的功能突出。为了提升卫星钟差预报精度,以满足实际应用需求,本文以卫星钟差周期特征为切入点,基于频谱分析方法和钟差QP模型提出了一种钟差预报的谱分析模型,并采用GPS卫星钟差数据进行预报试验。最后,以试验数据为参考依据进一步分析了谱分析模型与QP模型的钟差预报特征。结果表明,对于短期预报,谱分析模型的预报精度和稳定性优于QP模型;从长期预报实践看,谱分析模型的预报偏差会明显加大。另外,使用不同种类星载原子钟,两种模型的预报结果和稳定性也会不同。

