自适应预测补偿的迭代制导方法及其应用研究
何 勇,王 健,宋征宇,柴嘉薪,胡海峰
(1. 北京航天自动控制研究所,北京 100854;2. 中国运载火箭技术研究院,北京 100076)
0 引 言
迭代制导在美国土星5号火箭上的应用是一个重要的里程碑,也是首次将闭环最优制导方法应用于运载火箭。之后,美国的航天飞机,法国的“阿里安”火箭、俄罗斯的“能源”火箭以及我国的长征系列运载火箭也都采用了迭代制导技术,并取得了良好的效果。
迭代制导是以最优控制原理为基础,通过解析公式在线计算到达目标轨道所需的速度增量、位置增量,并依此规划出最佳飞行程序角,能够满足火箭终端轨道参数的约束。然而,如韩祝斋提出的经典迭代制导算法中,为避免破坏火箭飞行系统的稳定性,又能获得足够高的制导精度,对系数,,,分别做提前取零处理,能够实现关机时刻的精确控制,但对于各系数取零至发动机关机时刻,由于干扰造成的迭代制导与标称弹道计算的终端程序角偏差,以及发动机后效冲量偏差导致的入轨参数偏差却无法进行修正。在实际的发射任务中,很多有效载荷对星箭分离时的姿态是有要求的,若没有独立的调姿系统,轨道精度与终端姿态两者难以兼得。
针对迭代制导停止计算后的入轨参数和满足终端程序角约束要求的运载火箭制导问题,均有一些学者进行过相应研究。其中:前者的研究主要是吕新广、宋征宇介绍的CZ-7大推力直接入轨采用的轨道预测的方法;后者的研究主要集中于以下3个方面:1)将控制姿态角的最优解析表达式,通过二阶近似,展开为与时间相关的二次函数,用以同时满足入轨点速度、位置和姿态角约束的迭代制导方法,如文献[7-9];2)采用直接法来计算满足轨道和程序角约束的制导方法,如文献[10-12];3)采用数值积分的方法对制导参数进行反馈修正,进而得出同时满足入轨姿态约束和轨道参数约束要求的制导指令,如文献[13-14]。
文献[15]提出了采用预测-修正方式来求解迭代制导计算过程中高阶微分方程的解析解,并指出这种方式比线性微分校正的方式更优,但仍无法对迭代停止后的参数偏差进行校正。为此,本文在经典迭代制导算法的基础上,针对如何修正迭代制导停止计算后的入轨参数或终端程序角偏差这一问题,根据迭代制导计算的终端程序角和飞行视加速度的预测模型,对关机点参数进行补偿,并依据补偿后终端指标重新规划飞行轨迹,提升现有迭代制导算法对入轨参数或终端程序角偏差修正的适应能力。
1 迭代制导基本原理
火箭进入真空飞行后,其动力学方程可在目标轨道坐标系下,即以地心为原点′,′轴为由地心指向目标点,′轴在目标点轨道面内指向飞行方向,′轴与′轴、′轴构成的右手正交坐标系下简化为:
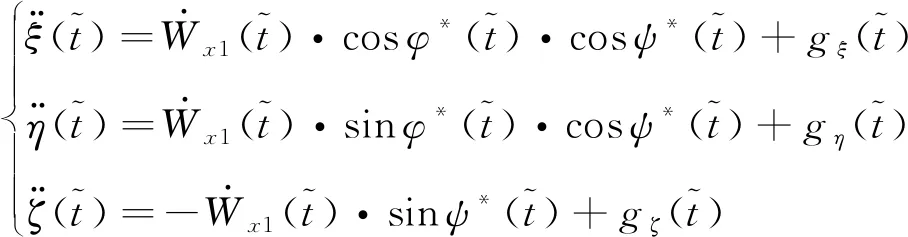
(1)


图1 俯仰和偏航程序角的定义


(2)
对于液体运载火箭来说,推力平稳,其比冲和流量可近似为常值,则式(2)可进一步写成:

(3)
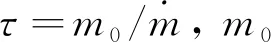
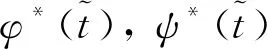

(4)
对于液体火箭发动机燃料最省可表示为时间最短,即性能指标函数可表示成:
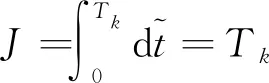
(5)


(6)


(7)
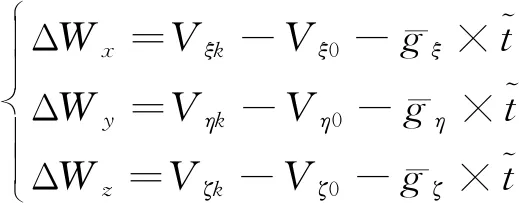
(8)

(9)
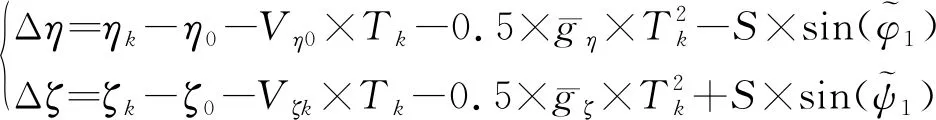
(10)

2 自适应预测补偿的迭代制导
2.1 问题提出
运载火箭经典迭代制导方法,是将关机时刻的轨道参数作为控制量来进行控制,能够实现在需要关机点上精确关机,但对于在迭代制导停止计算后的入轨参数或终端程序角偏差却无法进行修正。例如,在飞行推力变大且存在干扰的情况下,会导致迭代制导计算的俯仰方向终端程序角与标称弹道计算的程序角会出现大偏差的情况,使得关机后的推力矢量方向偏离了标称弹道的要求,即本文2.2.3节提出的后效推力矢量大偏差,造成入轨精度变差甚至超出飞行任务的指标要求,如图2所示。
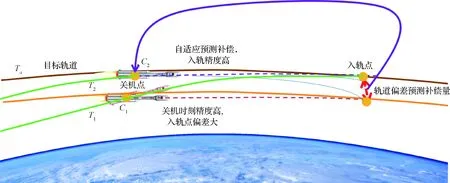
图2 两种算法对入轨参数偏差修正的飞行示意图
图2中表示采用经典迭代制导的飞行轨迹,在关机点关机后,根据理想的关机时刻程序角和后效作用,其入轨点恰好位于目标轨道上。但由于关机时刻程序角偏差的存在以及推力方向不再调整,在后效作用下的最终轨道与目标轨道产生了较大的入轨偏差,如图中所处的轨道。表示采用预测补偿的方法得到的飞行轨迹,其中轨道偏差的补偿量采用预测的方法进行计算,并且补偿到关机点的状态约束中,此时关机点更新为,在同样的推力方向和后效作用下,重新调整到目标轨道上。
此外,对于一些飞行任务,也存在需要制导计算的程序角满足终端姿态约束的情况,如2.2.4节提出的终端姿态角约束。
2.2 自适应预测补偿迭代制导算法
..基本原理
自适应预测补偿迭代制导方法基本原理为:

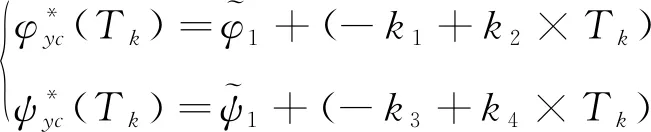
(11)
2) 构建迭代制导停止计算后的视加速度变化模型()为:

(12)

()的计算方法可采用以下两种方式:
(1)采用标称弹道计算的视加速度模型进行计算:如本文2.2.3节,对于现役运载火箭来说,发动机试车试验能够获得发动机后效的精确模型,并据此得出后效段的视加速度预测模型;
(2)采用当前时刻加速度计测量得出的视加速度进行计算:如本文2.2.4节,调姿段采用调姿起始时刻的加速度计测量得出的视加速度进行计算,其原因是由于调姿段的时间很短,燃料消耗量相比当前运载火箭的质量很小,其对视加速度的影响可忽略不计;
3) 根据(1)和(2)的参考模型,计算关机点参数偏差补偿量,即迭代制导计算终止时刻至关机时刻或入轨时刻(考虑发动机后效的情况下)的速度增量与原终端状态约束的偏差,可表示成与迭代停止时刻火箭的状态、程序角以及后续飞行过载等相关的函数,其表达式为:

(13)
4) 对关机点参数进行补偿,得修正后的关机点参数为:
=+Δ
(14)
5) 根据补偿后的关机点参数,重新划飞行轨迹,进而得出满足入轨参数或终端程序角偏差修正的制导指令。
上述是自适应预测补偿的基本原理;针对不同的应用,式(13)的表示形式和计算方法各有不同,将在2.2.2、2.2.3和2.2.4中进行详细阐述。
..发动机关机策略的变化
为降低入轨前过载及发动机后效影响,会采用依次关闭发动机的方式,如下图和文献[1]提到的两两关机方式:

图3 发动机推力变化示意图
但这会使关机时间间隔内的推力变化剧烈,影响迭代参数估算的准确性和程序角大范围波动,进而产生较大姿态跟踪误差,导致入轨精度变差。
在此背景下,在第一次关机前松弛位置约束,以保证姿态跟踪平缓,但这会造成系统性的入轨偏差;在主动段的迭代制导是基于四台发动机工作而进行规划的,当切换为两台发动机工作时,也会产生入轨偏差。
由于四机段和两机段之间的后效段工作时间短,故可忽略其影响,为此,依据两台发动机和四台发动机工作时两体动力学方程,分别预测这两种工况下在终端时刻对应的速度、位置。在真空飞行段,两体动力学方程可简化为:

(15)

对式(15)进行求解可得关机时刻对应的速度、位置为:

(16)
其中,
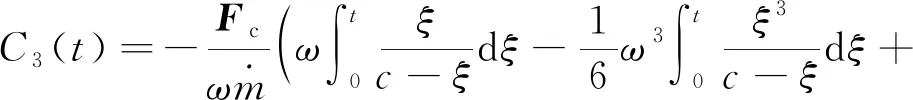


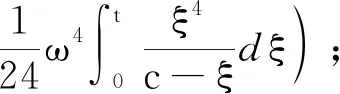




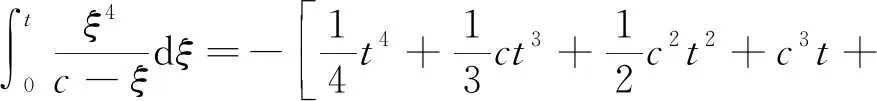



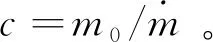

..发动机后效推力方向的偏差

在实际飞行过程中,由于外界干扰的影响,如发动机推力的变化,会出现迭代制导与标称弹道计算的终端程序角偏差较大的现象,如图4所示,使得由于后效推力的方向发生了较大的变化,导致后效推力造成的轨道偏差变大,进而使得入轨精度变差。图4中,,分别为俯仰、偏航迭代程序角;0、1%、2%、3%、4%、5%和Ref分别为推力额定、1%、2%、3%、4%、5%和标称弹道对应的俯仰、偏航迭代程序角的变化曲线。

图4 不同推力偏差工况下迭代程序角变化示意图
本节与“考虑终端姿态约束”的区别在于,前者是在迭代制导与标称弹道终端程序角存在偏差情况下,对发动机的后效进行补偿,后者是将迭代制导终端程序角规划到指定的参数值。
根据式(11)计算终端时刻的俯仰、偏航程序角,其表达式为:

(17)
根据标称弹道计算的视加速度模型进行计算后效段产生的速度增量在目标轨道坐标系下的表示为:
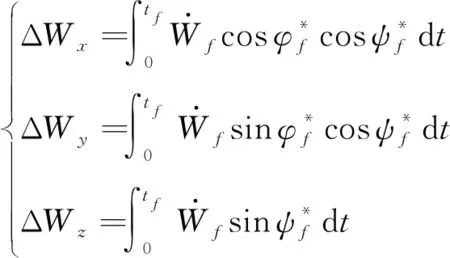
(18)

同时,根据标称弹道的俯仰、偏航终端程序角,并参考式(18),可得到标称弹道的后效冲量大小为:
[ΔΔΔ]
则关机时刻所需的补偿量表达式为:
Δ=[Δ-Δ, Δ-Δ,
Δ-Δ, 0, 0, 0]
(19)
..终端姿态约束
2.2.3节是对于入轨姿态约束要求较低或者无约束情况下进行相应的迭代制导计算,本节是对于一些用于完成对地定向、测控等任务的卫星,其对入轨姿态有着严格的要求,使得运载火箭需满足一定的姿态约束要求。为此,在迭代制导预测的当前时刻离发动机关机时刻的时间差小于0后,停止迭代制导计算,并进入姿态快速调整段,将程序角0,0调整到预先设置的,程序角上,以俯仰程序角为例,其调姿段的表达式为:
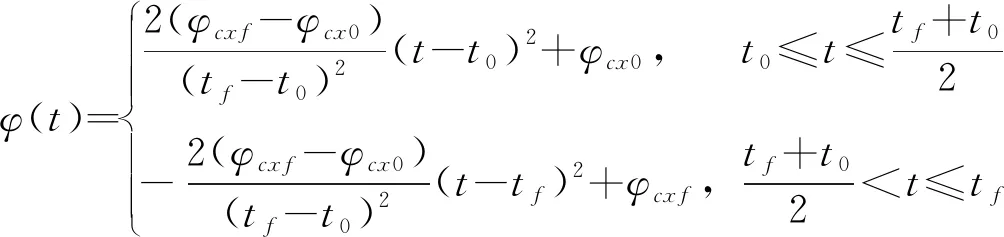
(20)
式中:()表示时刻对应的调姿段的俯仰程序角;,表示调姿起始和终止时刻,则+0为预测的关机时刻。偏航程序角调姿公式与式(20)类似,不再重复。
调姿段的视加速度表达式可写成:

(21)
式中:为发动机比冲;为质量燃尽的时间。
结合姿态调整和视加速度的变化规律,可得从调姿开始时刻至发动机关机时刻+0的视速度增量变化为:

(22)
从调姿开始时刻至发动机关机时刻+0的位置增量为:
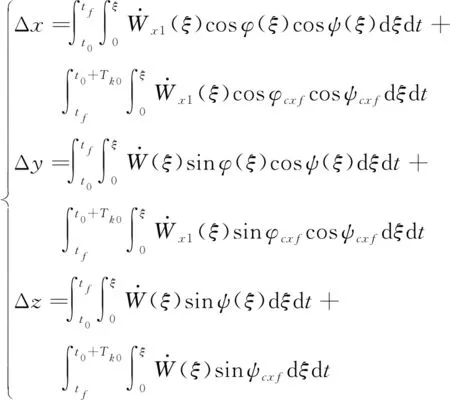
(23)
同理,可求出不考虑调姿调整时对应的视速度和位置增量,记为[Δ1Δ1Δ1],[ΔΔΔ],则关机点参数偏差的补偿量可表示为:

(24)
本节中的调姿开始时刻、调姿终止时刻以及发动机关机时刻+0之间的关系如图5所示。

图5 调姿时序图
图5中,为以起飞为零点的飞行时间,0为以迭代制导停止计算为起点的相对时间;程序角的保持段是用于提升姿态角跟踪程序角的效果。
3 仿真校验
3.1 仿真条件
本文2.2.2节所提的算法在文献[1]中给出了仿真用例及其试验分析结果,为此重点对2.2.3和2.2.4节所提的算法进行仿真校验。以某带助推两级运载火箭发射510 km×520 km的太阳同步轨道任务为仿真用例,对本文算法进行仿真校验。
为偏于本文叙述,选取二级迭代制导的启动时刻为零点,发动机后效结束时刻为入轨点,其在目标轨道坐标系下的初值如表1所示:

表1 迭代制导计算初值
表中:“用例1”为额定状态下获得的初值;“用例2”为二级发动机秒流量取5%正偏差状态下获得的初值。
发动机性能参数为:总推力为165 kN,比冲为4295.0 m/s,后效冲量产生的速度增量为13.3 m/s。
关机和入轨时刻的轨道参数如表2所示。

表2 关机和入轨时刻轨道参数
标称弹道的俯仰和偏航终端程序角分别为-7.0°和-12.5°。
以上数据与实际飞行任务的数据存在差别,但不影响对本文算法校验的正确性。
3.2 终端程序角大偏差工况
以表1两种工况为试验用例,分别采用经典迭代制导(简称经典方法)和本文所提方法进行计算和比较,得到用于控制的俯仰和偏航程序角如图6、图7所示。

图7 偏航迭代程序角变化示意图
图6中,分别表示用于控制的俯仰和偏航程序角;后缀为0表示采用经典方法计算得出的相应参数;后缀为1表示采用本文方法计算得出的相应参数。
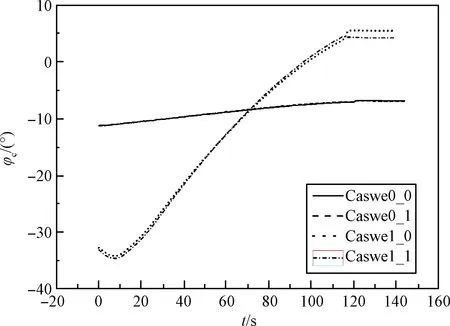
图6 俯仰迭代程序角变化示意图
可以看出,本文所提方法计算得出的制导程序角与经典方法的大小和变化趋势的一致性较好,表明采用本文方法计算得出的制导程序角作为控制输入与经典迭代制导的效果相当。控制精度如表3和表4所示,虽然关机时刻制导精度稍差,但这是因为提前考虑了后效偏差的结果,因此在入轨时刻,精度提升效果很明显。
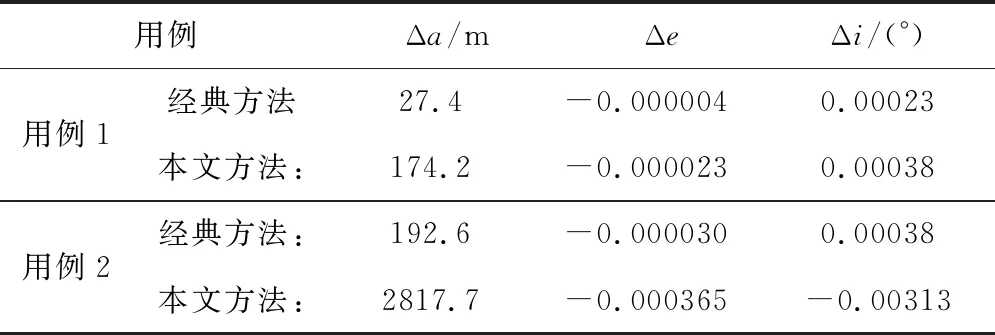
表3 关机时刻轨道参数
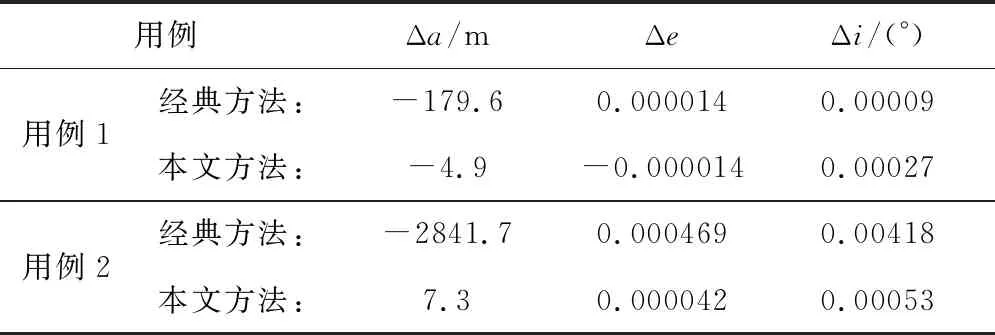
表4 入轨时刻轨道参数
表3和表4中的Δ, Δ和Δ分别表示关机和入轨时刻的实际与标称弹道的半长轴、偏心率和轨道倾角的偏差量,其迭代终端时刻的俯仰和偏航程序角偏差量如表5所示。
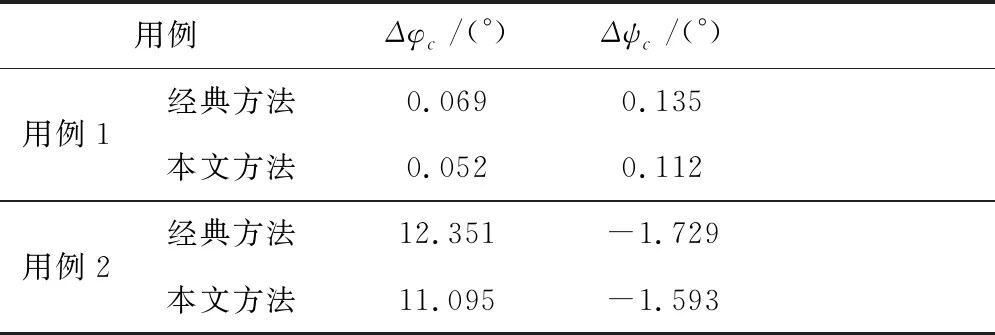
表5 迭代终端程序角偏差
从表3至表5可看出:
1) 由于用例1工况的迭代制导与标称弹道计算的终端程序角偏差较小,为0.2°范围以内,使得采用本方法的补偿量较小,近似于0,故入轨参数偏差量与经典迭代制导的大小相当;
2) 当迭代终端程序角偏差变大时,如用例2程序角偏差超出11°工况,相比于经典迭代制导方法来说,采用本方法对入轨参数偏差的提升达85%以上,如表6所示。尤其是半长轴制导控制偏差,由“公里级”提升为“米级”。

表6 入轨参数偏差提升百分比
3.3 终端姿态约束工况
仍以表1中的用例1为例,分别采用经典迭代制导(简称经典方法)、文献[7, 9]采用的制导方法(简称二次曲线方法)和本文所提的自适应预测补偿迭代制导方法进行计算和比较,得到用于控制的俯仰和偏航程序角如图8、图9所示。

图8 俯仰迭代程序角变化示意图
图9中:,分别表示用于控制的俯仰和偏航程序角;后缀为0表示采用经典方法计算得出的各参数;后缀为1表示采用本文方法计算得出的各参数;后缀为2表示采用二次曲线方法得出的各参数。

图9 偏航迭代程序角变化示意图

表8 迭代终端程序角偏差
表7中入轨参数的偏差表明:相比于二次曲线方法来说,采用本文方法得出的偏心率和轨道倾角偏差较大,但对于运载火箭的入轨精度来说,仍具有较高的精度,且从图8、图9可看出,本文所提方法计算得出的制导程序角与经典方法的大小和变化趋势的一致性较好,程序角的变化幅度也较小,这说明本文方法对推力偏差工况的适应能力较好。
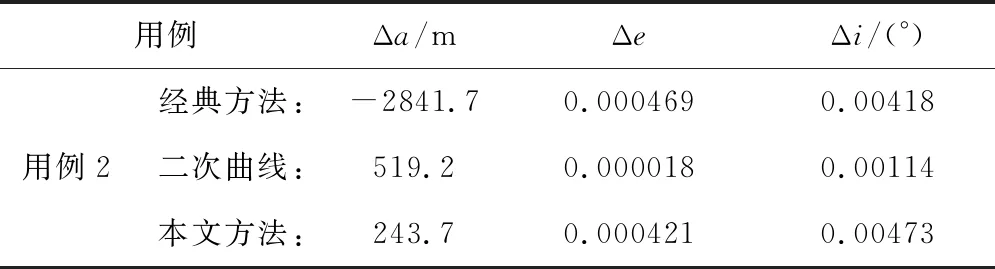
表7 入轨时刻轨道参数
为提升运载火箭燃料的使用率,通常会增加用以调节燃料混合比的利用调节系统,混合比的调整也会导致推力出现波动。这里仅以利用系统调节2次为试验用例,即:在迭代制导启动70~80 s时采用高工况模式,推力增加7500 N;在迭代制导启动100~110 s时采用低工况模式,推力降低7500 N。此时,三种方法的入轨精度如表9所示。
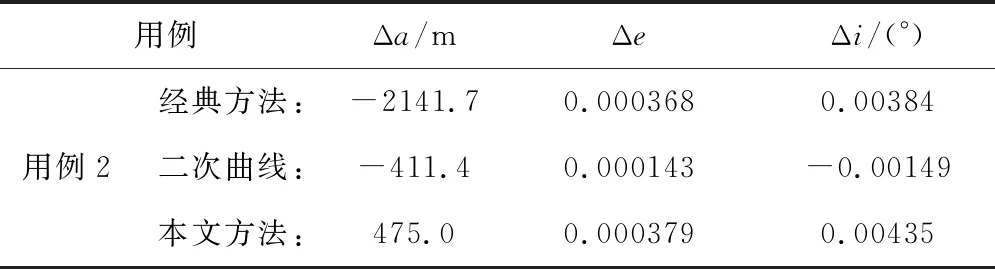
表9 入轨时刻轨道参数
从表9可看出,采用二次曲线方法的入轨参数偏差仍最优,但相比于其他方法来说,其程序角的变化幅度最大,如图10、图11所示。

图10 俯仰迭代程序角变化示意图

图11 偏航迭代程序角变化示意图
从图10、图11可看出,当推力出现波动时,采用本文方法在满足终端姿态约束要求的同时,其计算得出的用于控制的俯仰和偏航程序角的品质较好,且终端程序角的偏差最小,如表10所示。

表10 迭代终端程序角偏差
4 结 论
本文针对已有迭代制导停止计算后的入轨参数或终端程序角偏差无法修正这一难题,提出了一种基于模型参考的自适应预测补偿迭代制导方法,并以某运载火箭发射任务为研究对象进行了仿真分析与比较,结果表明:与现有迭代制导方法相比,本文采用的自适应预测补偿的迭代制导方法,在提升迭代制导对入轨参数或终端程序角偏差的修正能力、实现高精度入轨或降低终端程序角偏差的同时,也对推力的偏差具有较强适应性。此外,本文所提的方法在某运载火箭首飞任务中的应用效果也表明:本文的方法能够提升有效载荷的入轨精度,且有效避免了采用现有迭代制导方法因后效冲量矢量方向的大偏差导致发动机定时关机的现象。

