高维离散分布数据集中NSD算法精度、敏感度校正及应用

韩孝明

(吕梁学院 汾阳师范分校，山西 汾阳 032200)

离群点检测作为数据挖掘的重要手段已在各个领域得到了广泛的应用[1-2].基于密度的LOF离群点检测算法在当下比较流行，但由于算法过于复杂且其准确性受到参数选择的深度影响，因此应用于高维离散数据集时准确率并不理想[3-5].本文提出了一种基于数据对象密度差异计算的NSD离群点检测算法，通过对比数据对象密度和在截取距离内与其相邻区域点的密度来判断对象的离群趋势.NSD算法计算过程简单，计算结果准确，具有很高的效率.

1 问题描述

在众多的数据集离群点检测方式中，基于密度的LOF检测算法最具典型性，它通过计算数据集中各数据对象的间距，即在事先设定相邻数据对象数量的前提下计算对象的最高分布密度，然后以此为基础确定特定对象的离群系数.离群系数越大，对象成为离群点的可能性越高.由此可见LOF算法通过离群系数的数值大小判断对象的离群倾向[6-7].然而，该算法必须对所有的对象逐一进行密度和离群系数的计算，且一旦参数选择不当就难以获得准确的结论.基于以上分析，优化算法流程、降低参数因素干扰能够有效提高算法的准确度，具体可通过以下集中方式进行.

(1)设定一个数据点截取距离，以数据对象为中心，以该距离为半径划定一个圆形区域作为数据对象的相邻区域，取代LOF算法按数量选择相邻数据点的方式，对象离群程度越高，区域内相邻点越少，由此可减少计算量.

(2)直接以区域内的相邻点数量描述对象的密度，取代LOF算法通过数据点间距值进行密度计算的方式，进一步简化计算流程.

(3)对所有没有相邻数据点的对象进行统一赋值，无需计算数据集中每个数据对象的离群系数.

以上几点即为NSD作为LOF优化算法的设计思路.

2 NSD算法设计

每一个数据集X中都包含了数据的K种属性，xi、xj分别为从数据集中随机选取的两个数据对象，dist(xi，xj)为二者在数据集中的距离，其表达式为

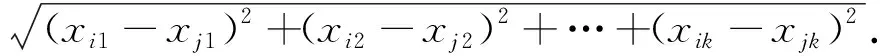
(1)

基于数据属性的不同设定一个截取距离R，由此可定义在dist(xi，xj)≤R的条件下由所有与目标对象距离为dist(xi，xj)的数据所组建的数据集为目标对象xi的邻域系统NR(xi)，其构成如图1圆形区域所示.

对于图1中的多属性数据集，C1、C2、C3分别为其中的三个属性簇，O1、O2是两个离群数据点.以C2簇中的目标对象xi为中心，以截取距离R为半径的邻域系统内包含xm，xn，xj，xl4个数据点，因此xi的邻域系统可表示为

NR(xi)=

{xm，xn，xj，xl}，∣NR(xi)∣=4.

图1 邻域系统示意图

邻域系统中数据点密度den(xi)的表达式为

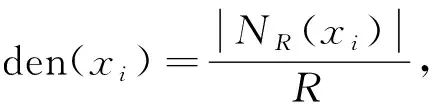
(2)

由上式可见，NR(xi)中数据点数量越多，则其密度越大.同时，

0≤den(xi)≤(N-1)/R,

N为数据集中数据点的总数量.

不同对象的邻域系统密度如图2所示.

图2 不同对象的邻域系统密度

图2中的三个圆形区域分别为正常数数据对象xi与离群数据对象O1、O2的邻域系统，它们的半径即截取距离是相同的.xi在C2属性簇中的邻域系统包含了4个数据点，O1在C1属性簇中的邻域系统同样包含了4个数据点，而O2的邻域系统是空的，按照邻域系统密度的定义，数据对象xi和O1的邻域系统密度均为4/R，而数据对象O2的邻域系统密度为0.

在以邻域系统中数据点数量描述系统密度的前提下，数据对象xi在多属性数据集X中的离群度NSD(xi)的计算方式为

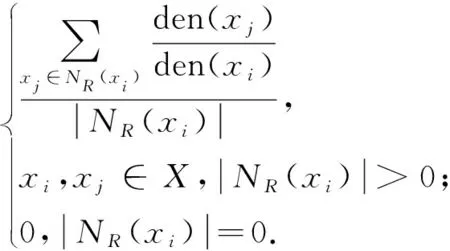
(3)

当∣NR(xi)∣>0时，上式可转换为

(4)

离群度数值与目标对象的离群程度存在以下几种对应关系.

(1)当NSD(xi)=0时，表明目标对象的邻域系统中没有数据点，xi不属于任何属性簇，离群程度较高.

(2)当NSD(xi)>1时，表明目标对象的邻域系统中虽然存在一些数据点，但xi与这些数据点各自邻域系统的密度存在较大差异，即xi与这些数据点并不属于同一个属性簇.

(3)当NSD(xi)≈1时，表明xi与其邻域数据点各自邻域系统的密度近似相等，二者位于同一属性簇的可能性较大.

(4)当NSD(xi)<1时，表明xi的邻域系统密度大于其邻域数据点的邻域系统密度，是数据集中较为常见的现象.

由此可见，对于数据集中的任意一个数据对象xi，如果其离群度为0，则可认定其为离群点，如果其离群度大于1，则说明对象的离群趋势比较明显.数据对象离群程度如图3所示.

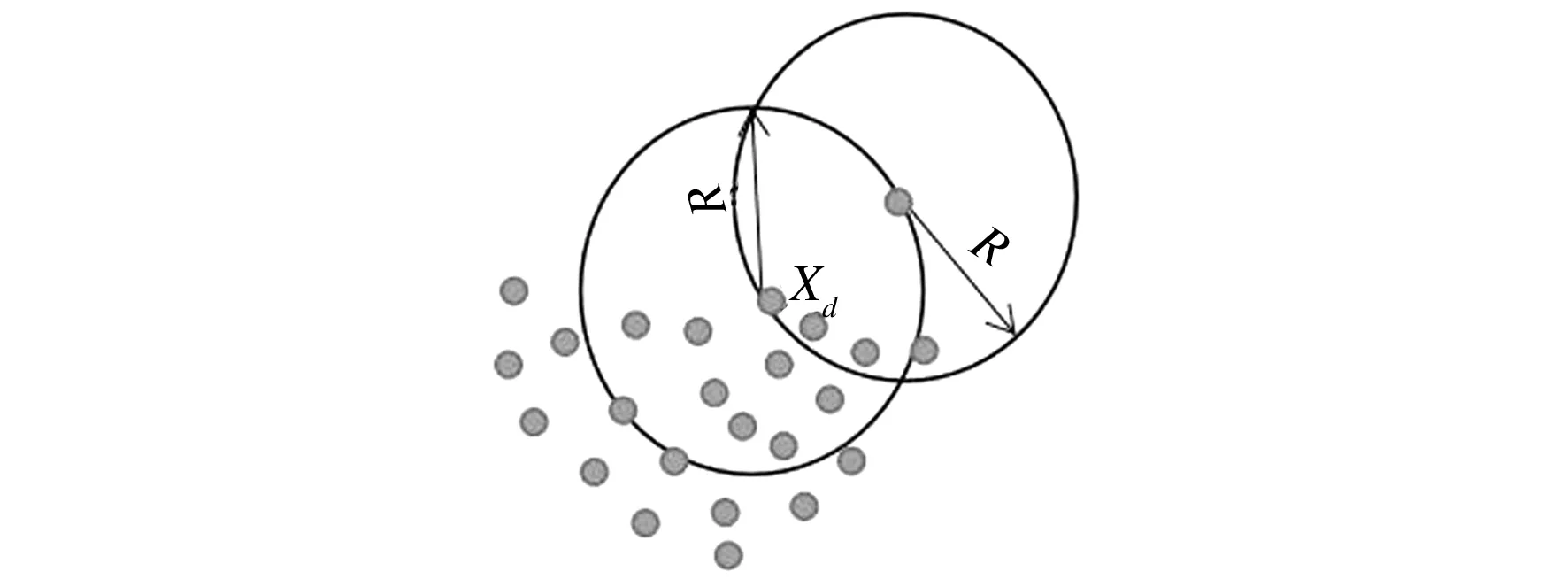
图3 数据对象离群程度示意图

在图3中，xd为离群点O1的邻域系统数据点之一，在半径同样为R的xd的邻域系统中包含了19个数据点，那么xd与O1的邻域系统密度比为

den(xd)/den(O1)=(4/R)/(19/R)=19/4，

即二者的邻域密度相似性量化数值为4.75.通过式(4)可计算出NSD(O1)=3.8125，说明O1具有明显的离群趋势.相比之下，对于图2中C2属性簇内的正常数据对象xi，其邻域系统密度为4/R，

NSD(xi)=1.25，

与1较为接近，说明xi基本不具离群可能性.

在确定数据集X中任意数据对象xi的离群程度时，如果仅通过xi邻域系统的密度进行判断，那么当对象位于数据点分布较为稀疏的属性簇中时发生误判的可能性极大，因此NSD算法基于数据对象本身及其领域数据点各自的邻域系统密度相似性进行离群趋势判断，从而保证了离群度判定的准确性.算法流程如下[8-11].

输入：k维数据集X，截取距离R，n.

输出：NSD算法判定的离群点编号.

3 测试与分析

选取国外某网络入侵记录数据集进行离群点检测，该数据集为高维数据集，特征维度多达41个，共包含50000个数据点，其中离群点数量为1500个，各数据对象最小间距值为1.5，对象最少有1个临近数据点数量.分别通过本文设计的NSD算法与现有的CBOF、LDOF、LOF算法进行检测并对比检测结果，以验证NSD算法的性能与检测准确性.本次测试用计算机采用Intel Corei 5处理器、主频为2.5 GHz、4 GB内存、安装Windows 7专业版操作系统，算法软件运行环境为MATLAB 2016A.

由于NSD算法的关键参数为截取距离R，而其它3种算法的关键参数为近邻参数k，所以需要对各算法的参数敏感性进行计算，以反映其对不同算法检测准确率的影响程度，具体计算公式为

(5)

式中：m为实验次数，参数变化速率为设定值.

以所选数据集为基础，按数据点数量为10000、20000、30000、40000、50000创建5个不同规模的数据集，通过上述算法对各数据集分别进行离群点检测，准确率结果如表1所列.

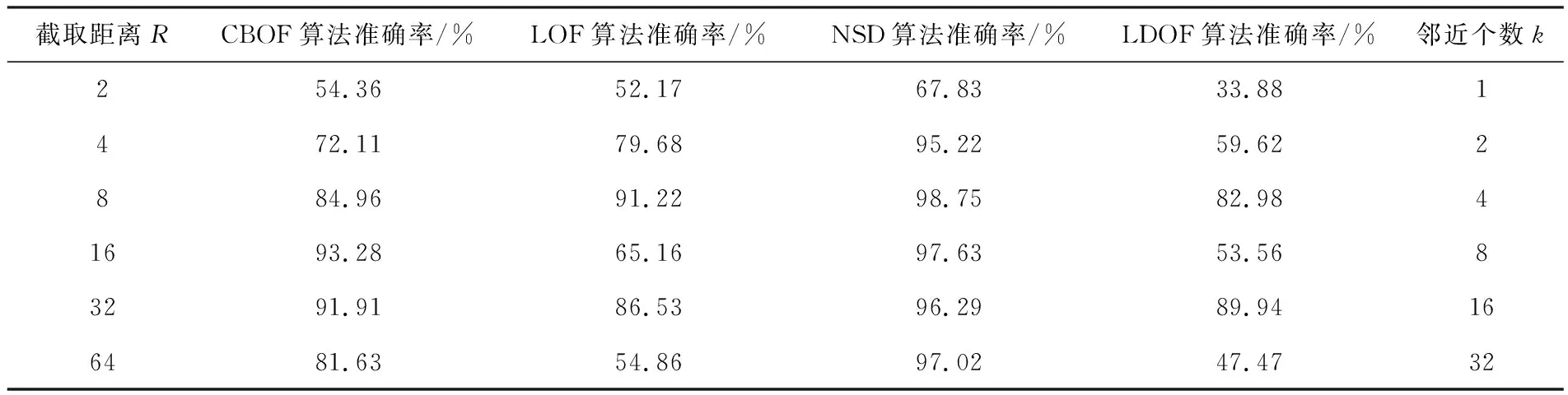
表1 不同算法的离群度检测准确率对比

由表1中的数据可见，在各种关键参数设定的条件下，NSD算法的离群点检测准确率均高于其它3种算法，截取距离为较小值2时，准确率较低，而延长截取距离后检测准确率均达到90%以上.同时，通过表中数值计算各算法的参数敏感性，结果为

S(NSD)=24.72，S(CBOF)=34.01，
S(LOF)=45.03，S(LDOF)=52.98，

对比可见NSD算法的参数敏感性较低.

在不同数据规模下对NSD算法的R及其它算法的k取最优值，得到最高检测准确率条件下的算法运行效率，具体结果如表2所列.

表2 不同算法的运行效率对比

由表2中的数据可见，各算法的运行时间随数据集规模的扩大而延长，而在相同数据规模的条件下NSD算法的运行时间均比其它3种算法短，由此可认定NSD算法具有更高的运行效率.

4 结语

为了有针对性地解决传统离群点检测算法参数敏感性高、准确率低的问题，本文提出了一种基于邻域数据对象密度差异的NSD离群点检测算法，通过目标对象与其邻域数据点的密度相似性判断其在数据集中的离群程度，相较于传统的LOF算法，本文所设计的算法优化了计算流程，提高了计算结果的准确性并降低了参数对计算精度的影响，对于各邻域数据挖掘技术的发展具有重要意义.