Volterra型微分-积分方程的数值格式构造及理论分析

罗紫洋, 安文静, 张新东

(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)

0 引言

Volterra型微分-积分方程(VIDEs)源于19世纪末20世纪初,是在竞争或人口增长模型中所引入的一类具有积分内核的方程.VIDEs中的积分项具有记忆性质[1],这一性质是其在物理领域有着广泛应用的重要原因.例如: 粘弹性方程[2]、具有记忆性的热传导方程[3-4],以及核反应堆中的热交换过程等.由于求解此类方程的解析解较为困难,因此研究此类方程的数值解具有重要的理论价值和实际意义.

处理微分-积分方程的主要方法为差分法.1897年,Volterra[5]在其著作中对该类方程的数值解法已有所研究.1974年,Brunner[6]采用隐式Runge-Kutta方法求解Volterra型微分-积分方程,并分析了此类方程数值解的稳定性.1992年,陈传淼等[7]利用内积近似一类微分-积分方程的积分项,并对空间项采用有限元方法,得到了相应的误差估计.1993年,汤涛[8]运用梯形求积技巧构造了一类微分-积分方程中积分项的数值格式,使其时间误差收敛阶可以达到Ο(τ3/2),并给出具体的理论分析.2005年,Shahmorad[9]基于Tau方法分析了线性Fredholm-Volterra型微分-积分方程的有效误差.2006年,Amiraliyev等[10]在均匀网格中构建Volterra型微分-积分方程的数值格式,并证明该格式的时间收敛阶为一阶均匀收敛.2008年,徐大[11]在希尔伯特空间中分析验证了有限差分方法求解线性Volterra型方程的稳定性; 同年,Tari和Shahmorad[12]基于勒让德多项式研究二维线性Fredholm积分方程,并给出了数值格式的误差边界.2010年,Wazwaz[13]提出结合Laplace变换和Adomian分解法,构造非线性Volterra型微分-积分方程的数值格式,并通过实验证明该方法的有效性; 与此同时,Zarebnia[14]利用Sinc方法求解Volterra型微分-积分方程,并验证该方法所具有的优良性,不仅收敛速度较快,且不存在当使用其他数值方法时常见的不稳定问题.2021年,Cimen和Cakir[15]基于正交规则和积分恒等式构造了一类Fredholm型微分-积分方程一种新的差分格式,并分析证明该格式的稳定性和收敛性.2022年,Santra和Mohapatra[16]利用复合梯形公式逼近Volterra型微分-积分方程中的积分项,使其误差时间收敛阶为Ο(τ).

本文考虑如下Volterra型微分-积分方程(VIDE)：

(1)

其中：Ω=[0,L]×(0,T],空间L>0,且时间T>0；积分核K(x,t-s)在Ω上光滑且有界；f,φ,g1和g2为给定的光滑函数.

1 紧致差分格式推导

为方便起见,本文中不同地方的常数C可以代表不同的数值.给定两个正整数M和N,定义h=L/M为空间变量x的步长,τ=T/N为时间变量t的步长,所以

xj=jh,j=0,1,…,M,
tn=nτ,n=0,1,…,N.

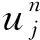
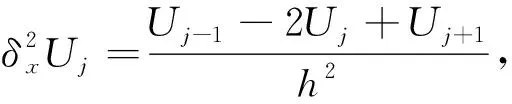
(2)

由复合梯形求积公式可得

(3)

其中：R为整个区间的截断误差.由

和中值定理可得

(4)

引理1[17]假设s(x)∈C6[a,b],则有

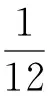
其中：ξj∈(xj-1,xj+1),j=1,2,…,M-1.

接下来对方程(1)进行逐项分析.对于方程(1)的时间项来说,利用Taylor展开，可得

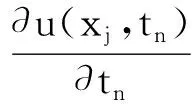
(5)

对于方程(1)的空间项来说,

(6)

对于方程(1)的积分项而言,由式(3)和(4)可得

(7)

如果对方程(1)作用H算子，可得

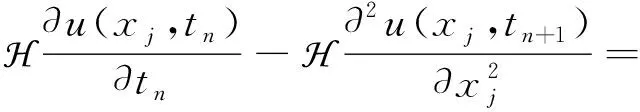
进而由式(5)、(6)和式(7)可得

(8)

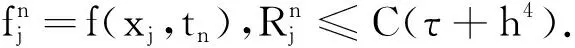
省去式(8)中的截断误差,当j=1,2,…,M-1且n=1,2,…,N时得到方程(1)的离散格式如下:

(9)

2 稳定性分析

本节将利用能量不等式的方法讨论数值格式的稳定性,并证明数值格式为无条件稳定.首先给出一些符号说明和引理.定义Vh为空间网格函数,Vh={V|V=(V0,V1,…,VM),V0=g1(tn+1),VM=g2(tn+1)}.以下内积和范数在证明中将用到,

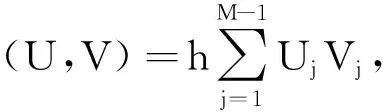
引理1[18]假设U∈Vh,则有

定理1紧致差分格式(9)是无条件稳定的,并且满足如下不等式：

其中：C为常数.

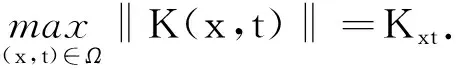
(10)

对式(10)两边同乘HUn+1,并在Ω上积分可得

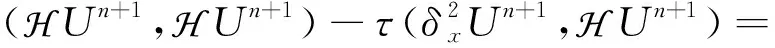
(11)

由引理1可知

由式(11)可得如下不等式，

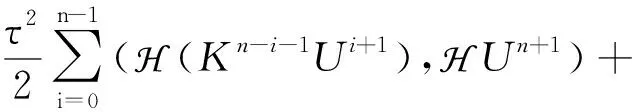
(12)

接下来将用归纳法证明.由式(12)可知,当n=0时，

(HU1,HU1)≤

(HU0,HU1)+τ(Hf0,HU1).

再由柯西-施瓦茨不等式可得

‖HU1‖≤‖HU0‖+τ‖Hf0‖≤
C(‖HU0‖+‖Hf0‖).

假设对任意k,k≤n时结论成立,即

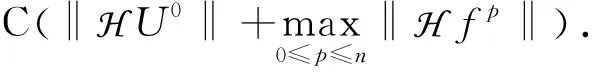
(13)

由式(12),当k=n+1时，有

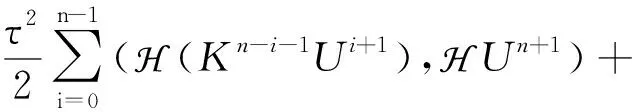
由上述不等式,结合式(13)可得

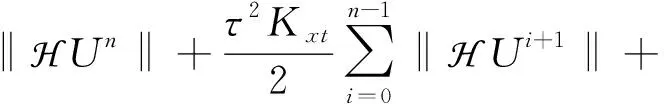
其中,C为常数.定理1证明完毕.

3 误差估计

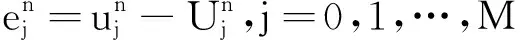
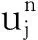
其中,C为常数.

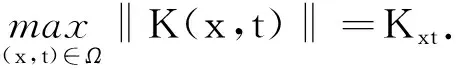
(14)

(15)

由引理1和式(15),有

(16)

类似定理1的证明,将采用归纳法.由式(16)可知,当n=0时，可得

假设对任意k,k≤n时，结论成立,即

(17)

由式(16),当k=n+1时，有

由上述不等式,结合式(17)可得

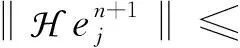
其中,C为常数.定理2证明完毕.

4 结论

本文通过有限差分方法构造了一类Volterra型微分-积分方程的数值格式,分析了格式的稳定性和误差估计,得到其误差收敛阶为O(τ+h4).相较于解决该问题原有的数值格式,在空间收敛阶上有进一步的提升.在今后的研究工作中,将以构建收敛速度更快,误差更低的数值格式为目标,并将此方法应用到分数阶微分-积分方程的数值求解.