考虑驾驶员有限理性下信号交叉口车速引导模型
李振龙, 杨磊, 张靖思, 董爱华
(北京工业大学城市交通学院北京市交通工程重点实验室, 北京 100124)
随着中国机动车保有量的迅速增长,城市道路的交通拥堵和污染物排放问题变得日趋严重。车辆在信号交叉口处频繁的加速、减速和停车是增加延误和污染物排放的重要影响因素[1]。在信号交叉口上游一定区域内引导车辆的速度,使车辆平顺的通过交叉口,有利于降低车辆的延误和污染物排放。绿波作为干线交通信号协调控制的一种方法,可视为一种简单的车速引导方法,车辆按照设计速度行驶,能够得到连续的绿灯信号,畅通无阻的通过所有交叉口。近年来车联网技术的发展,车辆可实时获得交通情况和信号灯信息,使车联网环境下车速引导成为现实。
中外学者对车速引导策略进行了深入的研究。鹿应荣等[2]以通过的车流量最大为优化目标,提出了加速和减速两种车速控制策略,加速控制策略目标为车辆到达停车线的时刻最小,减速控制策略目标为车辆到达停车线的速度最大,仿真验证了该速度引导策略可减小车辆通过交叉口的行程时间、燃料消耗和污染物排放。刘欢等[3]通过对车辆不同行驶状态能否通过交叉口进行判断,从而引导车辆加减速不停车通过交叉口,并利用VISSIM仿真软件和MOVES排放模型仿真验证了该速度引导策略,结果表明提出的策略能够显著减少延误和车辆排队长度。He等[4]提出了考虑前方车辆排队和引导车辆不影响后车通行双约束下的车速引导策略,构建了单目标车速引导优化模型。Zhao等[5]提出了考虑交叉口车速引导策略的车辆跟驰模型,并对比分析了不同引导区域长度、不同联网车辆比例下传统跟驰模型和改进跟驰模型的减排效果。Tang等[6]提出了考虑多交叉口车速引导策略的车辆跟驰模型,对比分析了传统跟驰模型和改进跟驰模型在能耗排放和通行效率方面的差异,仿真结果表明此模型能有效降低燃油消耗和平均停车时间。Barth 等[7]基于三角函数构建了动态生态驾驶引导速度曲线,生成的引导速度曲线光滑且加速和减速曲线部分连续可导。Lee等[8]基于最大通过率模型(maximized throughput model, MTM)、平滑速度模型(smooth speed model, SSM)和最小加减速模型(minimized acceleration and deceleration, MinADM),综合考虑交叉口下游的交通状况和车辆间的跟驰行为,建立了生态驾驶车速诱导系统。雷朝阳等[9]通过判断近信号控制区车辆通行特征和路口可通行性,以路口停车次数和车辆延误最小为优化目标,建立了目标函数,基于多目标粒子群算法求得车辆最优车速,并利用PerScan、Vissim和MATLAB/Simulink联合仿真验证了引导模型的有效性。
上述研究假设驾驶员是完全理性的,即100%遵从系统给出的引导车速,实际交通环境中,交通参与者是有限理性的。李涛等[10]基于西蒙的有限理性理论,针对交通参与者在两选择肢效用差小于一定阈值无法实现理性判断这一现象,提出了考虑出行者有限理性下的路径选择模型,发现模型能够较好的解释出行者在路径决策中的有限理性行为。张新洁等[11]考虑了出行者是有限理性的,建立了考虑无差异阈值和车位占用率的停车设施规划双层规划模型,采用某通勤廊道作为算例背景对模型进行求解,结果表明提出的模型具有更好的解释性,上述研究表明有限理性成为交通参与者行为建模中不可忽略的因素。
Tang等[12]提出了一个扩展的跟驰模型来研究驾驶员有限理性对微观驾驶行为的影响,仿真结果表明,考虑驾驶员的有限理性可以提高交通流在小扰动演化过程中的稳定性。Tang等[13]在车速引导模型中考虑了驾驶员有限理性相关因素,讨论了不同速度决策阈值、反应时间和执行水平下模型的减排效果,然而,描述有限理性的相关因素假设为固定的阈值,并不适用于整个驾驶员群体。鉴于此,采用有限理性二项LOGIT概率决策模型描述驾驶员的有限理性,并融入信号交叉口车速引导中,提出了考虑驾驶员有限理性下的车速引导模型。并以所构建的模型为基础,探究了油耗和通行时间的变化对驾驶员遵从引导车速概率值的影响,并从污染物排放和通行时间两方面量化了驾驶员有限理性对车速引导策略效益的影响,为未来车速引导系统的实际应用和设计提供了一定的理论参考。
1 考虑有限理性的信号交叉口车速引导模型
城市道路网中,交叉口是实现交通流转换方向的节点,车辆在交叉口附近频繁的加减速及停车是增加延误和污染物排放的重要影响因素,在交叉口一定区域内对车速进行引导,有利于提高交叉口的通行效率和减小车辆通过交叉口的能耗及排放。王东磊[14]提出了以车辆不停车通过交叉口为优化目标的车速引导模型,称为传统车速引导模型。
当车辆以初始速度到达交叉口为红灯时,如图1所示,此时车辆若以道路最高限速到达交叉口为绿灯,速度引导系统提供的引导速度即为道路最高限速vmax。若车辆按道路最高限速行驶仍会遇到红灯,将进行减速引导。传统车速引导模型可表示为[14]
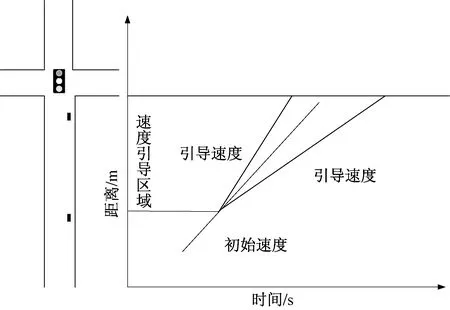
图1 传统车速引导模型示意图
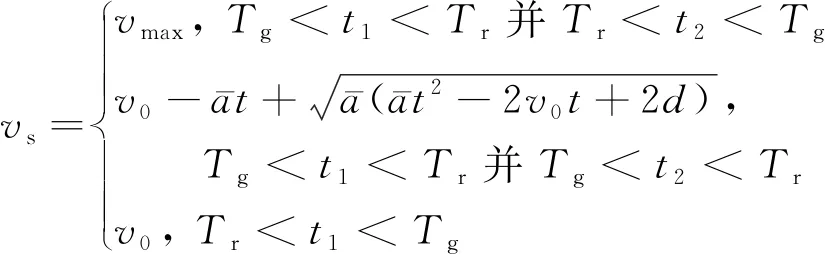
(1)
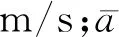
传统车速引导模型假设驾驶员完全遵从引导速度,实际交通环境中驾驶员是有限理性的,并不会完全遵从引导速度。引入驾驶员决策模型来预测驾驶员是否会遵从引导速度,其中LOGIT模型被广泛应用于相关交通决策问题中[15-16],当车辆驶入交叉口前的速度引导区域时,驾驶员通过HMI(human machine interfaces)得知遵从引导速度通行时间和油耗的变化。随后,驾驶员根据HMI提供的车速引导信息决定是否遵从引导速度。将驾驶员遵从引导速度定义为选择肢A1,不遵从引导速度定义为选择肢A2,U1和U2分别为两选择肢的效用,分别由固定项(Vi,i=1,2)和随机项(εi,i=1,2)组成,其表达式分别为
U1=V1+ε1
(2)
U2=V2+ε2
(3)
式中:固定项V1、V2分别为两选择肢效用中确定的部分,表示通行时间和油耗的线性组和;随机项ε1、ε2相互独立且服从期望为0的Gumbel分布。
两选择肢效用固定项的差值是驾驶员决策的重要依据,根据相关研究[15-16],将两选择肢效用固定项的差值V2-V1定义为
V2-V1=a+b1(T2-T1)+b2(O2-O1)
(4)
式(4)中:T2、T1分别为驾驶员选择A2、A1后车辆的通行时间,即为车辆按当前速度和系统引导速度行驶通过引导区域和驶出交叉口的时间,s;O2、O1分别为驾驶员选择A2、A1后车辆通过交叉口的油耗,L/100 km;a、b1、b2为模型的参数。
驾驶员选择A1的概率P1和选择A2的概率P2表示,其表达式分别为
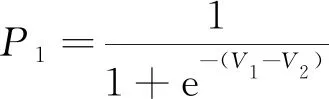
(5)
P2=1-P1
(6)
选择模型[式(5)]为传统BL模型,传统BL模型仅在两选择肢效用差值明显时,才能准确预测出决策者的选择。当两个选择肢效用差值不明显时,由于忽视了个体对可供选择方案的难以抉择的可能,预测会不准确。Krishnant[17]在传统BL模型中引入了效用阈值δ和偏好参数θ,当两选择肢效用差大于效用阈值δ时,驾驶员可以做出理性的选择;在效用差小于δ(大于-δ)时,决策者依据偏好θ进行选择。当θ=1时表示驾驶员完全偏好A1;当θ=0表示驾驶员完全偏好A2;当0<θ<1表示驾驶员的选择偏好,可表示为[17]
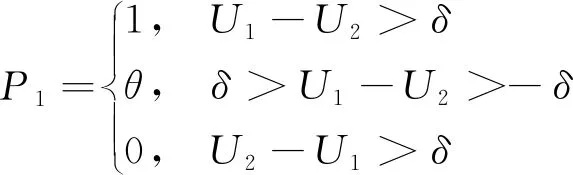
(7)
式(7)中:δ为效用阈值。
驾驶员遵从引导速度的概率P1为[17]
P1=Prob(U1-U2>δ)+Prob(|U1-U2|≤δ)θ
(8)
式(8)中:第一项和第二项表达式分别为
Prob(U1-U2>δ)=1/[1+exp(δ+V2-V1)]
(9)
Prob(|U1-U2|≤δ)=[exp(2δ)-1]{1/[1+
exp(δ+V2-V1)]}{1/[1+
exp(δ+V1-V2)]}
(10)
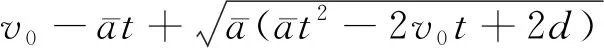
2 模型标定
采用Python和VSSIM搭建车速引导仿真实验平台,获取1 817组样本数据,每组样本包含遵从当前速度通过交叉口的时间T2和油耗O2,遵从引导速度通过交叉口的时间T1和油耗O1。以通行时间差T2-T1和油耗差O2-O1为判断依据设计驾驶员遵从“引导速度”意向调查问卷,根据问卷调查结果对样本数据进行标注。
参数θ、δ、a、b1、b2通过最大化似然函数L确定[10],可表示为
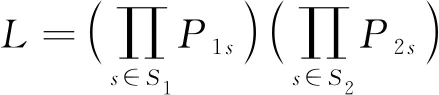
(11)
式(11)中:S1为遵从引导速度的驾驶员集合;S2为不遵从引导速度的驾驶员集合;P1s为驾驶员s遵从引导速度的概率;P2s为驾驶员s不遵从引导速度的概率;L为样本量的似然函数。
采用遗传算法求解此最优化问题,遗传算法是模拟自然界自然选择及遗传学机理的求解算法,能够自适应控制搜索过程求得最佳解。式(11)可转换为最大化lgL,且满足如式(12)、式(13)约束。
δ≥0
(12)
0≤θ≤1
(13)
设置种群数为400,最大进化数为300,数据集为带标签的1 817组样本数据,求得参数值如表1所示。

表1 模型求解参数值
采用814组带标签样本数据验证此模型预测驾驶员遵从引导速度的准确性,准确率为78.9%。参数b1、b2均小于0,说明遵从引导速度的通行时间和油耗越小,驾驶员遵从引导速度的概率会越大。θ=0.73,说明驾驶员在A1、A2效用差值不明显时,更偏好于A1,不同T2-T1和O2-O1下驾驶员遵从引导速度的概率值如图2所示。图3中,有限理性LOGIT模型在效用差0值附近较为缓和,即A1、A2之间效用的微小差距不会另驾驶员选择概率产生大幅度变化,驾驶员在效用差小于一定程度时,会根据自身的偏好参数θ进行抉择,更能反映驾驶员实际的决策行为。
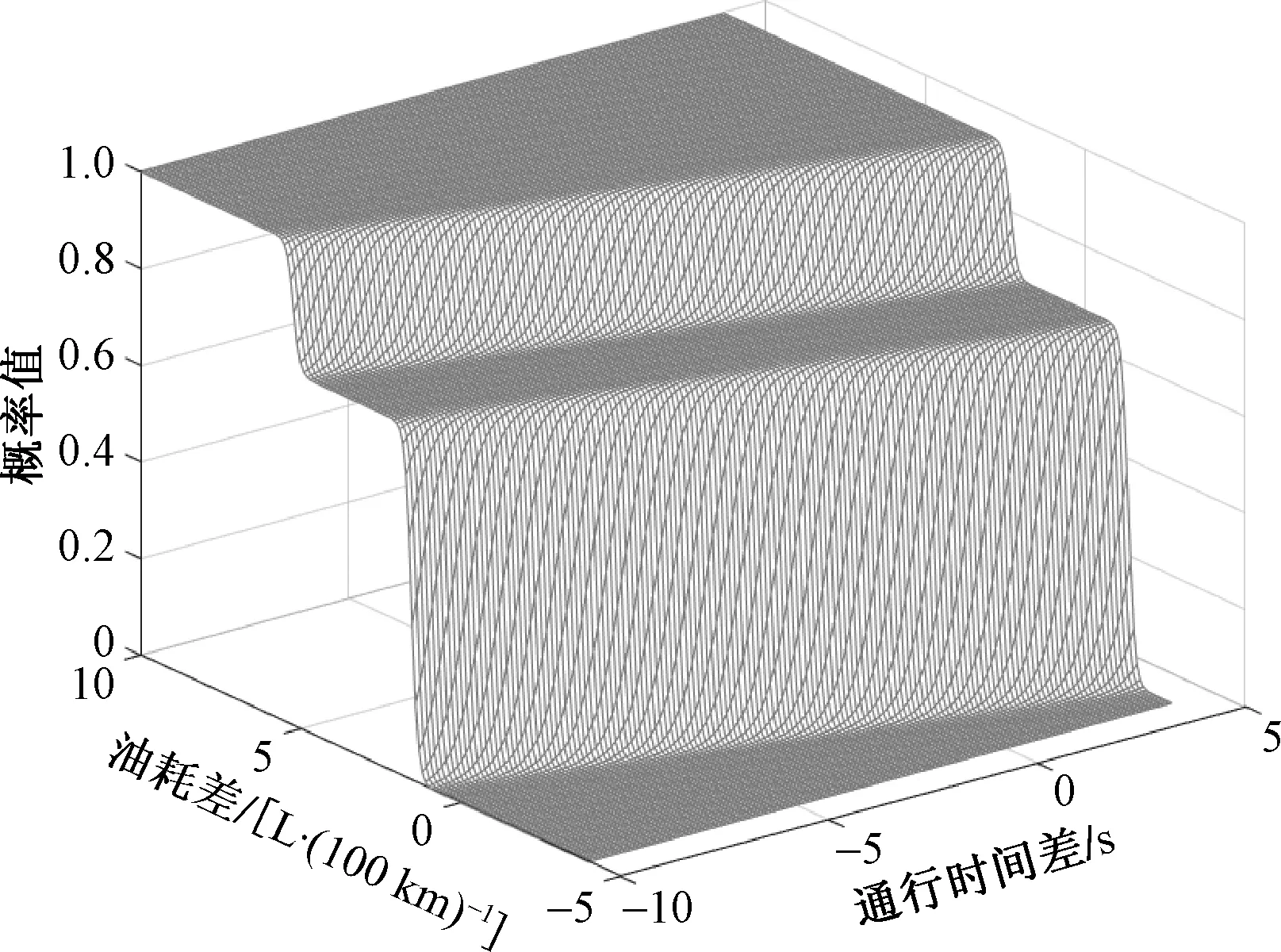
图2 T2-T1和O2-O1对驾驶员遵从引导速度概率的影响
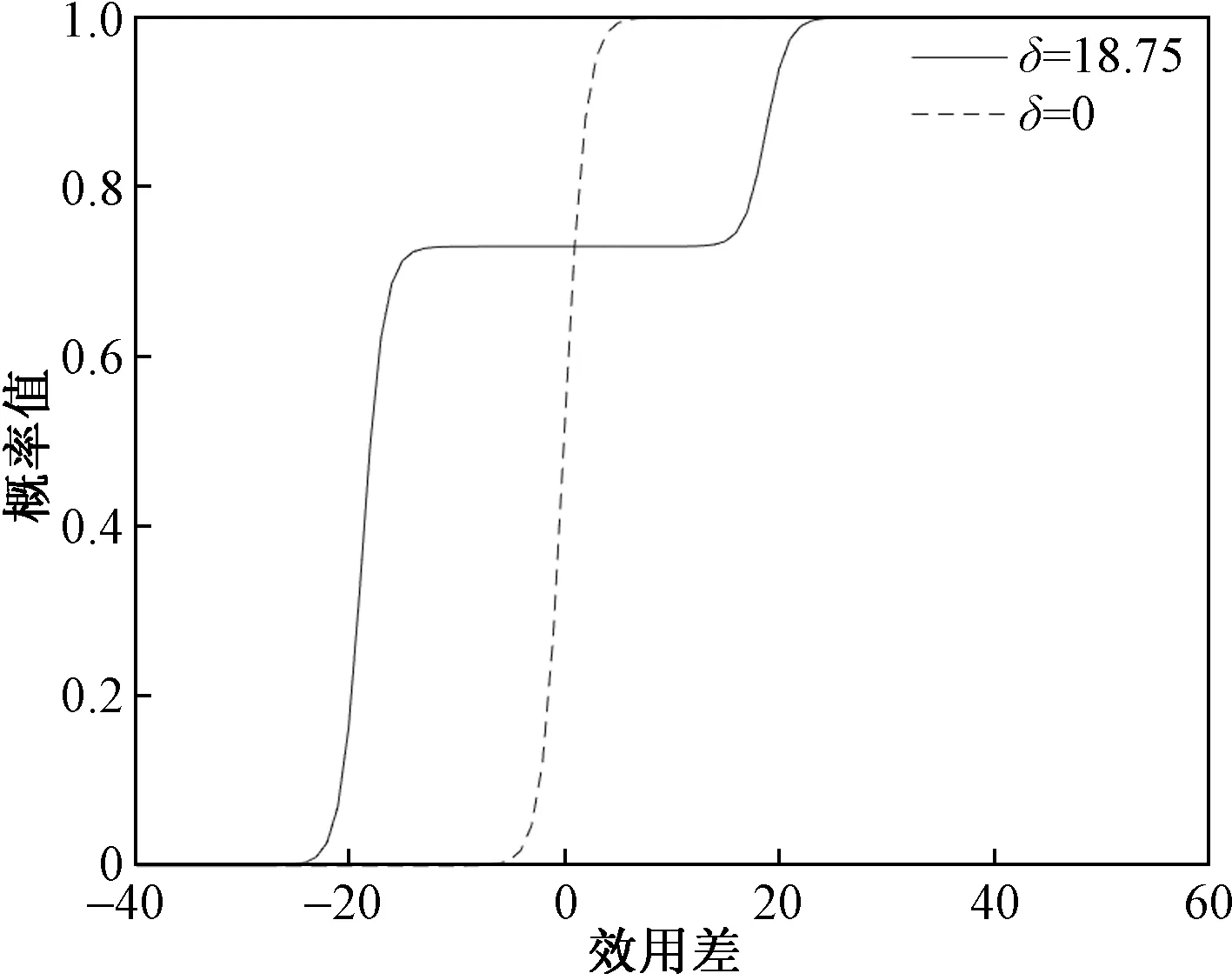
图3 传统LOGIT模型与有限理性LOGIT模型对比
3 模型仿真与分析
选取鼓楼外大街—安德路交叉口为仿真路口,对比分析无车速引导、有限理性车速引导和传统车速引导3种情况下的车辆污染物排放。速度引导区域为南北直行路段距离交叉口停车线200 m范围内的区域,交通流量和信号灯配时如表2所示。

表2 交叉口配时及流量
利用Python和VISSIM COM接口对VISSIM进行二次开发,实现信号交叉口车速引导,如图4所示。仿真时长设为4 800 s,仿真初始阶段路网并没有达到相对稳定的状态,因此选取900~4 500 s 仿真小时的数据进行分析研究。交叉口最高限速设为60 km/h,最低限速设为20 km/h。

图4 VISSIM仿真图
对不同车辆排放模型比较选择,确定了基于机动车比功率VSP分布的车辆微观排放模型计算车辆的污染物排放[18]。输入车辆构成固定,计算VSP时,车辆因素为常量,没有考虑道路坡度和海拔等相关因素,VSP与车辆速度v和加速度a关系见式(14)[18]。后根据不同VSP区间下的基准排放率,得到车辆通过交叉口污染物的排放量。
VSP=0.105 802v+0.001 353 75v2+
0.000 333v3+va
(14)
不同车速引导模型下车辆的通行时间及污染物排放如图5~图7所示。传统车速引导和有限理性车速引导下车辆平均通行时间较无车速引导分别增加6.5%和6.0%,CO2每公里排放量分别下降23.1%和19.2%,CO每公里排放量分别下降50%和42.3%。说明驾驶员的有限理性会对车速引导模型的通行效率和节能减排效果产生影响。
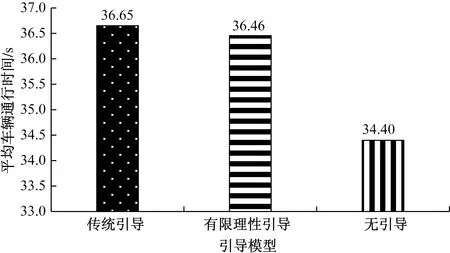
图5 不同车速引导模型下车辆通过交叉口平均通行时间
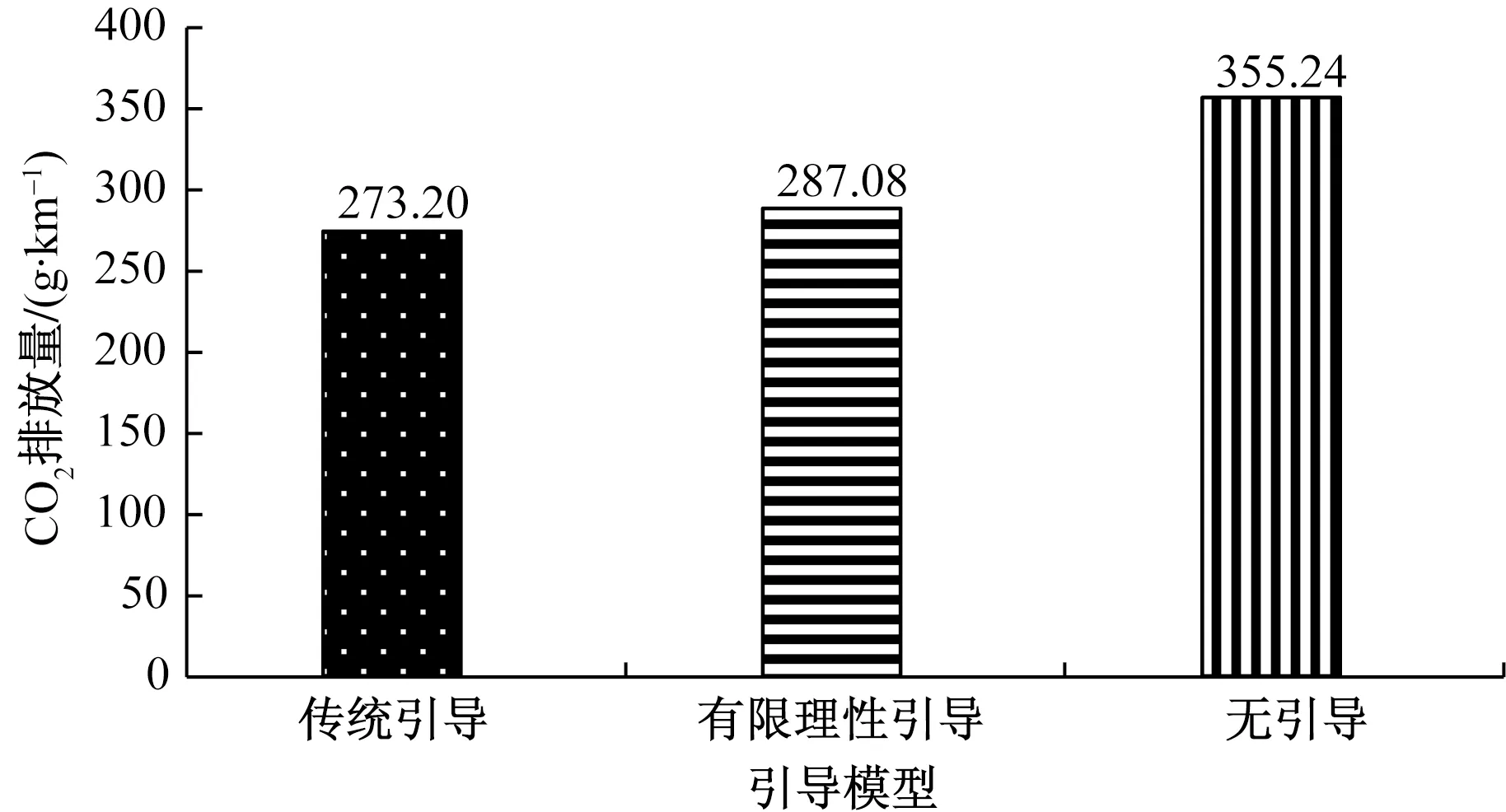
图6 不同车速引导模型下车辆平均二氧化碳排放
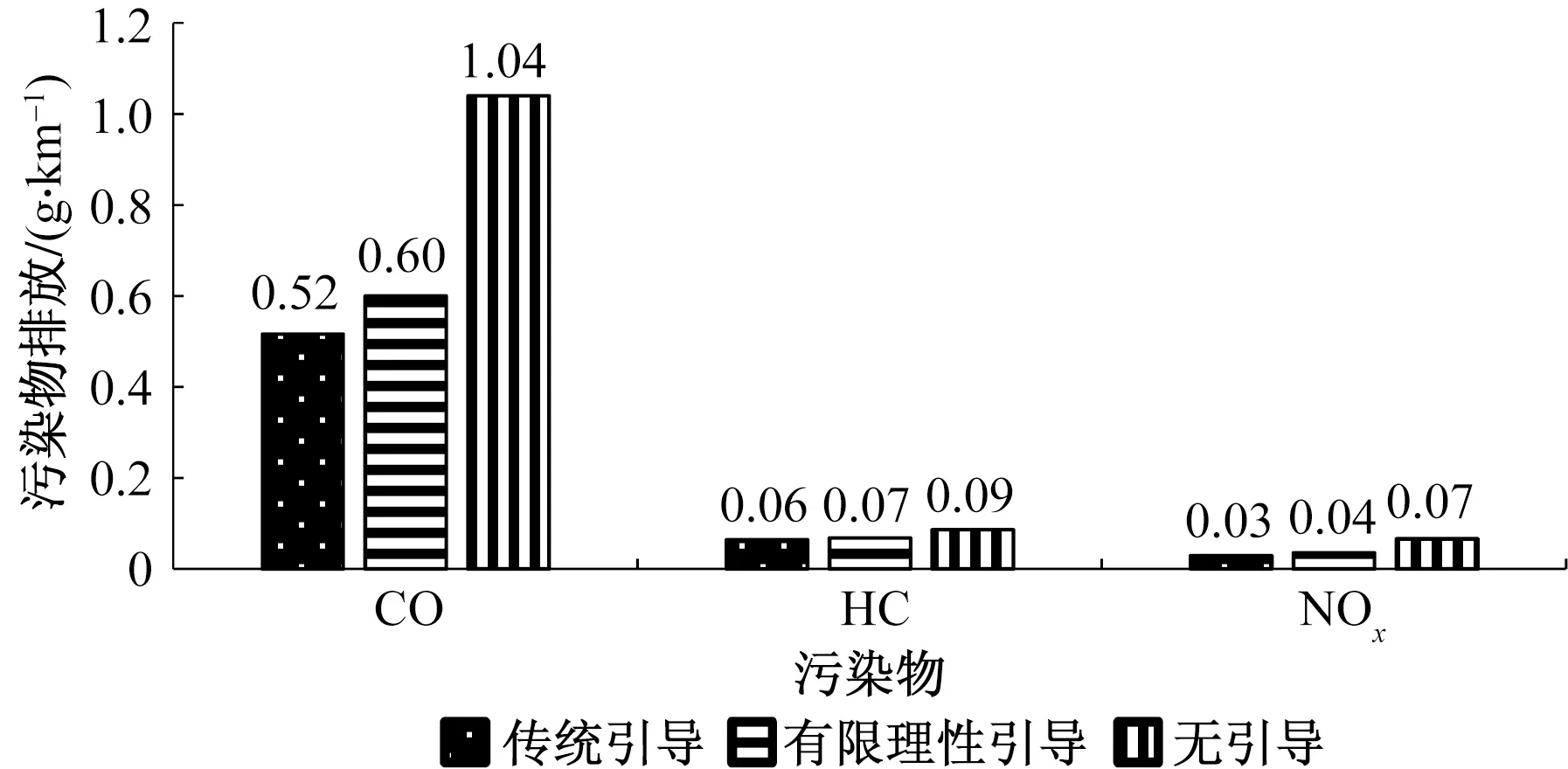
图7 不同车速引导模型下车辆平均污染物排放
4 结论
针对驾驶员对给出引导速度决策的非完全理性行为,建立了有限理性二项LOGIT决策模型,并融入交叉口车速引导中,提出了考虑驾驶员有限理性下的车速引导模型。通过微观交通仿真对比分析了无车速引导、传统车速引导和有限理性车速引导三种情况下的车辆通行时间和污染物排放,得出如下结论。
(1)驾驶员遵从引导速度决策问题上,当A1、A2的效用差绝对值小于阈值时,驾驶员依据自身的计算能力无法进行理性判断,会根据自身的偏好进行抉择,这种考虑实际情况的模型可为车速引导系统的实际应用提供参考。
(2)仿真量化了有限理性下车速引导模型的通行效率和减排效果。传统车速引导和有限理性车速引导下车辆平均通行时间较无车速引导分别增加6.5%和6.0%,CO2每公里排放量分别下降23.1%和19.2%。提出的模型较无车速引导降低了车辆的污染物排放,且考虑了驾驶员有限理性对遵从引导车速决策行为的影响。
有限理性二项LOGIT决策模型参数通过调查问卷和仿真数据计算得到,未来应该利用实地实验数据,提出一个更符合实际的考虑驾驶员有限理性的速度引导模型,研究驾驶员有限理性对信号交叉口系统的影响。

