基于SSA-BP的离港航班滑出时间预测
黄龙杨, 夏正洪, 贾鑫磊
(中国民用航空飞行学院空中交通管理学院, 广汉 618307)
滑出时间是指离港航班从停机位推出开车并滑行至跑道上实际起飞的时间间隔,它是评估繁忙机场场面运行效率的主要性能指标[1]。随着机场跑滑系统结构及其运行模式日益复杂,大型枢纽机场的离港航班平均滑出时间已高达25 min。目前,多数机场采用基于经验的滑出时间来对离港航班进行管制指挥,而实际滑出时间与经验滑出时间往往相差甚远,航班的过早推出或不恰当的滑出时机都将导致出现不必要的拥堵、延误和燃油消耗,并且将严重影响机场场面运行效率。因此,科学准确地预测离港航班的滑出时间,对于提升机场场面运行效率和协调决策能力,降低运行成本和污染排放至关重要。
国外的离港航班滑出时间相关研究成果主要集中在对其影响因素和预测方法的研究。其中,影响因素主要包括离港队列长度、滑行距离、地面交通流情况、跑道运行模式、天气状况、流控情况等;研究方法集中于排队论[1]、机器学习[2]、强化学习[3- 4]等。中国关于离港航班滑出时间预测的研究还处于起步阶段,刘继新等[5]分析了离港航班滑出时间的影响因素。冯霞等[6-7]基于排队论和支持向量回归(support vector regression, SVR)方法对单跑道机场的离港航班滑出时间进行了预测,但是所得预测结果精度仅为75%左右。邢志伟等[8]基于贝叶斯网络和LWSVR方法对滑出时间进行了预测方法,预测精度提升至85%左右[9]。Lian等[10-11]利用支持向量机预测离港航班的滑出时间,并基于滑出时间进行了推出策略的控制。Li等[12]基于深度学习方法对单跑道机场离港航班的滑出时间进行了预测。可见,现有研究成果主要以单跑道或者多条跑道中的一条跑道为研究对象,且预测结果的精度还需要进一步的提升。同时,基于支持向量机(support vector machine, SVM)和反向传播(back propagation, BP)神经网络的离港航班滑出时间预测结果对初始权值和阈值较为敏感、准确性和稳定性表现不佳。
为此,提出了一种基于麻雀搜索算法获取BP神经网络的最优权值和阈值的方法。首先分析了离港航班滑出时间的可量化影响因素及相关性,基于相关性分析结论构建了基于BP神经网络的离港航班滑出时间预测模型,创新性地使用麻雀搜索算法对BP神经网络的初始权重和阈值进行优化,并采用我国中南某枢纽机场2周的实际运行数据对预测模型进行了验证。以期通过对离港航班滑出时间科学准确的预测,优化其推出开车时刻和起飞时刻,从而提升机场场面运行效率,减少燃油消耗和污染排放。
1 滑出时间影响因素及相关性分析
1.1 影响因素
离港航班滑出时间(taxi out time, TOT)等于该航班离港实际起飞时间(actual take off time, ATOT)与实际撤轮档时间(actual off block time, AOBT)之间的差值,即
TOT=ATOT-AOBT
(1)
离港航班的滑出时间可以分为场面滑行时间和跑道外排队等待的时间两部分。其中,场面滑行时间主要与场面交通流的大小有关,同时还与滑行距离的长短、转弯个数、机组习惯、天气等因素相关;同时段滑行的离港航班、进港航班数量越多,场面滑行时间可能越长,滑行距离越长则滑出时间也会相应的增长。跑道外排队等待的时间主要与进港流量大小、航空器间隔配备、流量控制以及天气等因素的影响。鉴于流量控制、机组习惯、天气等因素不可量化,故仅考虑可量化因素对离港航班滑出时间的影响,主要包括同时段滑行的离港航班数量、同时段滑行的进港航班数量、同时段推出的离港航班数量、半小时平均滑出时间、滑行距离、转弯个数等。
1.2 参数定义
(1)同时段滑行的离港航班数量x1,单位:架次。离港航班i可能与同时段滑行的离港航班j争夺跑道和滑行道资源,两者可能因滑行冲突导致滑出时间的增长。
(2)
式(2)表示航班j的实际起飞时间tATOT(j)刚好落在航班i的实际推出开车时间tAOBT(i)和实际起飞时间tATOT(i)之间的离港航班数量num(j)之和。
(2)同时段滑行的进港航班数量x2,单位:架次。离港航班i可能与同时段滑行的进港航班j争夺跑道和滑行道资源,由于进港航班优先级通常高于离港航班,因此可能因滑行冲突导致离港航班滑行时间的增长。
(3)
式(3)表示航班j的实际落地时间tALDT(j)刚好落在航班i的实际推出开车时间tAOBT(i)和实际起飞时间tATOT(i)之间的进港航班数量num(j)之和。
(3)同时段推出的离港航班数量x3,单位:架次。离港航班i可能与同时段推出的离港航班j争夺机坪和滑行道资源,可能因避让冲突而导致滑行时间的增长。
(4)
式(4)表示航班i的实际推出开车时间tAOBT(i)刚好落在航班j的实际推出开车时间tTOBT(j)和实际起飞时间tATOT(j)之间的离港航班数量num(j)之和。
(4)以30 min为时间片的平均滑出时间x4,单位:s。机场地面交通流呈现典型的时变特征,在离港早高峰、晚高峰以及进港高峰等典型繁忙时段,离港滑出时间会显著增加。目前,大型枢纽机场的离港航班平均滑出时间约为20 min,因此30 min平均滑出时间是衡量机场地面交通流状况的重要指标。
(5)
式(5)中:ti为在某个30 min时间片内的第i架离港航班的实际滑出时间;n为该30 min时间片的离港航班总数。
(5)离港航班滑行距离x5,单位:m。大型枢纽机场往往存在多个停机坪区域,离港航班滑出时间与其所在停机位的物理位置关系甚为紧密,滑行距离越长,则该停机位滑出的畅通滑行时间越长。
(6)转弯个数x6,单位:个。航空器直线滑行速度与转弯滑行速度有较大的差异,因此离港航空器在滑出过程中经过的转弯个数越多,则其滑行时间就会增加。根据停机位的位置和跑道滑行道运行模式,可获得离港航班的滑行路线,即可求得转弯个数。
1.3 相关性分析
所用数据来源于中南某枢纽机场2019年5月26日—6月8日的实际运行数据,数据集共有记录12 323条,包含离港航班5 747架次和进港航班6 576架次;每条记录由飞机呼号、机型、实际起飞时间、实际撤轮档时间、实际落地时间、跑道号、停机位等关键信息组成。通过对数据整理,删除重复及异常数据,并根据式(1)~式(5)依次得到同时段滑行的离港航班数量,同时段滑行的进港航班数量,同时段推出的离港航班数量,30 min平均滑出时间,滑行距离,以及实际滑出时间。最终得到样本数据5 200条,如表1所示。
基于SPSS软件对表1中的数据进行相关性分析,得到离港航班滑出时间影响因素的相关性分析结果如表2所示。
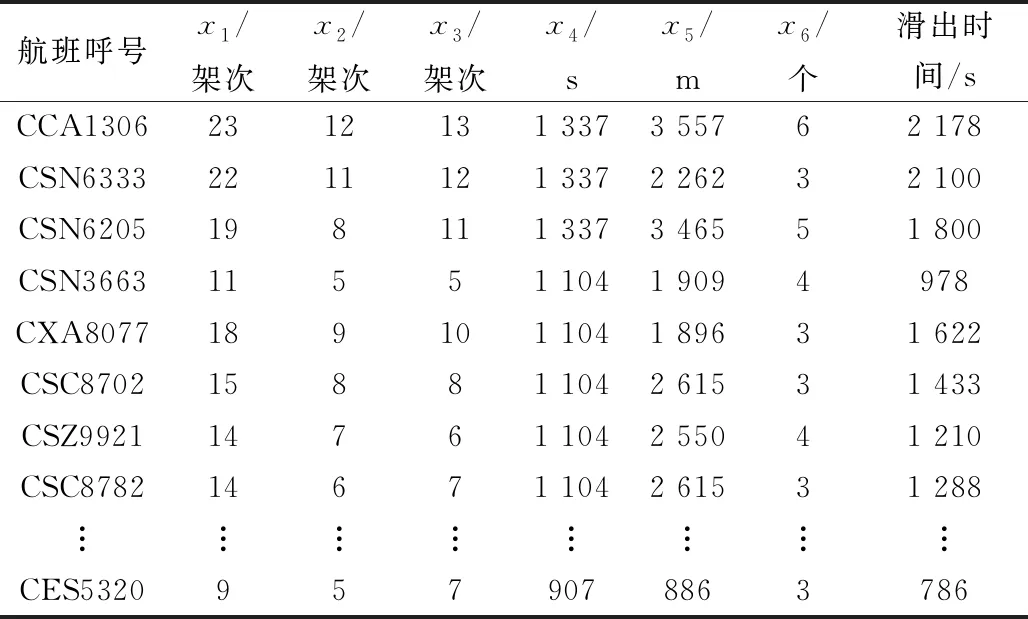
表1 样本数据

表2 相关性分析结果
可见,离港航班滑出时间与同时段滑行的离港航班数量强相关(r>0.7),与同时段滑行的进港航班、同时段推出的离港航班、半小时平均滑出时间均是中度相关(0.3 根据离港航班滑出时间影响因素相关性分析结论,选取强相关性和中度相关性的影响因素,构建基于BP神经网络的离港滑出时间预测模型如图1所示。其中,网络输入节点数为4,包括同时段滑行的离港航班数量x1,同时段滑行的进港航班数量x2,同时段推出的离港航班数量x3,以半小时为时间片的平均滑出时间x4,输出节点数为1。隐层节点数可根据输入节点和输出节点数先设置一个初始值,然后在此基础上逐渐增加,比较网络预测性能并选择性能最好对应的节点数作为隐含层神经元节点数,最终确定为7。 图1 基于BP神经网络的离港航班滑出时间预测模型 麻雀搜索算法是一种群体智能优化算法[13],目前已逐渐应用于故障诊断[14]、航迹规划等研究领域。它是一种基于麻雀的觅食行为和反捕食行为的群体优化算法,基本原理为:①发现者通常有较高的能量储备,负责搜索到具有丰富食物的区域,为加入者提供觅食的区域和方向;②一旦麻雀发现了捕食者,发出鸣叫作为报警信号,当报警值大于安全值时,发现者将加入者带到其他安全区域觅食;③发现者和加入者身份动态变化,但是各自所占种群数量的比重不变;④加入者的能量越低,则其所处的觅食位置就越差;⑤觅食过程中,加入者总能搜索到提供最好食物的发现者,并在其周围觅食;⑥当意识到危险时,群体边缘的麻雀会迅速向安全区域移动,以获得更好的位置,位于种群中间的麻雀则会随机走动,以靠近其他麻雀。其算法流程如下。 Step1初始化种群,迭代次数,初始化捕食者和加入者的比例。 Step2种群排序,得到当前的最优麻雀个体位置,以及最佳适应度值。 Step3觅食行为,按照式(6)更新发现者的位置。 Step4扩大觅食范围,按照式(7)更新加入者的位置。 Step5缩小觅食范围,按照式(8)更新警戒者的位置。 Step6反捕食行为,计算适应度值,更新麻雀种群位置,并更新最优适应度值。 Step7如满足停止条件则输出结果并退出,否则重复执行Step 2~Step 6。 发现者的位置更新规则为 (6) 式(6)中:Xi,j为第i个麻雀在第j维中的位置信息;t为当前迭代数;j=1,2,…,d,d为待优化问题的维数;α∈(0,1]为一个随机数;itermax为最大迭代次数;Q为正态分布的随机数;L为一个全1的行向量;R2和ST分别为警戒值和安全值,当R2 加入者的位置更新可表示为 (7) 警戒者的位置更新为 (8) 针对传统BP神经网络在离港航班滑出时间预测时存在对初始权值和阈值敏感、准确性和稳定性不好等缺点,利用麻雀搜索算法的觅食和反捕食行为不断更新种群的适应度和最优位置,从而获取BP神经网络的最优权值和阈值参数,然后再进行训练和仿真预测,其算法流程图如图2所示。 图2 基于SSA-BP的滑出时间预测流程图 选用麻雀搜索算法优化BP神经网络的初始权重和阈值。选取训练集与测试集整体的均方误差作为适应度。适应度函数越小,表示训练越准确,且兼顾模型的预测精度更好。首先从Excel中读取样本数据,确定网络的输入输出,划分训练集和测试集并将数据进行归一化处理;然后确定网络的拓扑结构,随机初始化网络的权值、阈值,麻雀种群规模、最大迭代次数、捕食者和发现者的比例等参数,以均方误差最小值作为最优适应度,将优化后麻雀位置信息作为权值与阈值赋给BP,并对SSA优化后的BP神经网络进行训练与仿真预测。 基于MATLAB中的神经网络工具箱进行编程,设置BP神经网络最大迭代次数10 000次,学习率为0.001,目标收敛误差为0.001;麻雀初始种群大小为50,最大迭代次数60,发现者和加入者占种群的比重均为0.5,能意识到有危险的麻雀占种群的比重为0.2。将样本数据集中随机抽取5 000个数据进行训练,则剩余的200个数据作为测试集,经SSA优化前后的BP神经网络预测值与真实值的对比[图3(a)],以及优化前后的误差对比[图3(b)]。 图3 SSA-BP与BP预测结果及误差对比 BP与SSA-BP两种预测模型均能实现对离港航班滑出时间的有效预测。基于SSA优化后的BP神经网络预测结果更接近于真实值,且误差分布更集中、更均匀。同时,从表3可以看出,基于SSA优化后的BP神经网络预测结果误差在±60 s内的准确率提升了20%,误差±180 s内的准确率提升了12%,误差±300 s内的准确率提升了7%。可见,所构建的模型输出结果比现有研究成果的预测精度高,从而验证了基于SSA-BP的离港航班滑出时间预测模型的有效性。但是,BP神经网络训练的效率一直以来都是神经网络的一个弊端,单独采用BP神经网络对这5 000个样本进行训练和200个样本预测所需时间约为35 s,而基于SSA优化后的BP神经网络训练和预测所需时间约为238 s。因此,精度的提升是以训练效率的降低为前提的。 表3 滑出时间预测结果误差分布对比 为进一步对基于SSA优化后的BP神经网络预测结果进行科学评价,以平均绝对误差百分比(mean absolute percentage error, MAPE)、平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)来进行验证,结果如表4所示。 表4 离港航班滑出时间预测精度评价 可见,基于SSA优化后的BP神经网络预测结果较优化前的MAPE提升了2.61%,MAE减少了11.73 s,RMSE减少了61.03 s。以上数据充分证明了所构建的基于SSA-BP的离港航班滑出时间预测模型和方法是合理的。 (1)提出了一种基于麻雀搜索算法获取BP神经网络的最优权值和阈值的方法,并应用于离港航班滑出时间预测模型。 (2)离港航班滑出时间与同时段滑行的离港航班数量强相关,与同时段滑行的进港航班数量、同时段推出的离港航班数量、平均滑出时间中度相关,与滑行距离和转弯个数弱相关。 (3)基于SSA优化后的BP神经网络预测结果准确率有显著提升,MAPE提升了2.61%,MAE减少了11.73 s,RMSE减少了61.03 s。 (4)下一步的工作重点将放在基于滑出时间预测的离港航班推出及滑行控制策略研究方面。1.4 模型构建
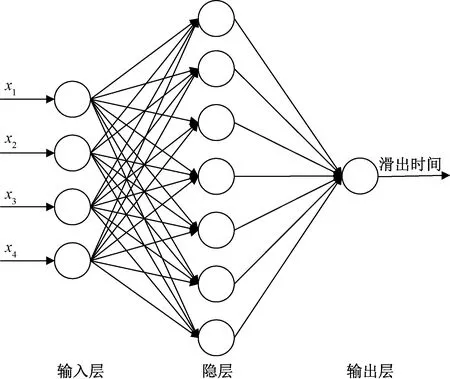
2 基于SSA-BP的滑出时间预测模型
2.1 SSA算法
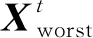
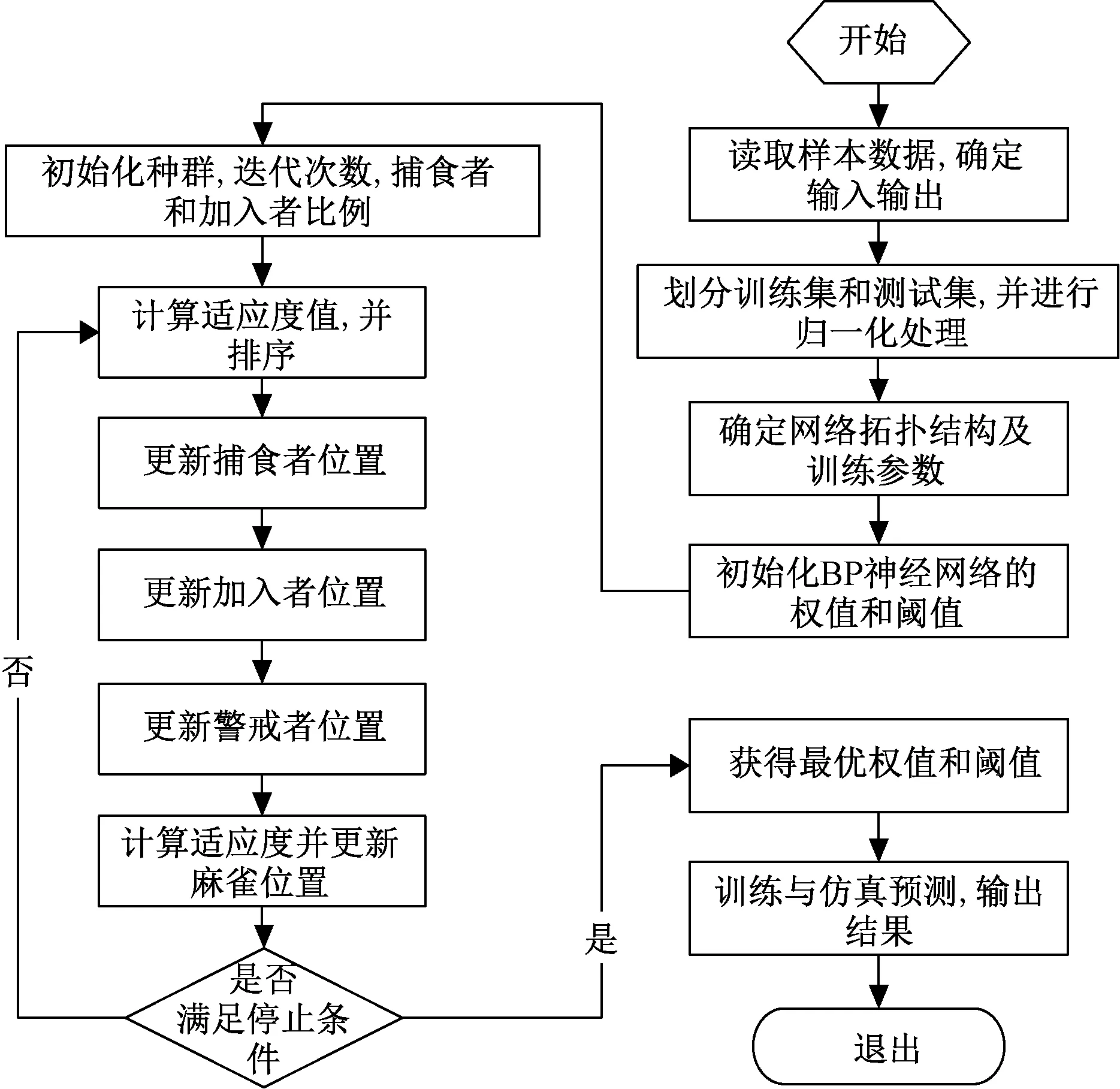
2.2 SSA-BP预测模型
3 滑出时间预测结果分析
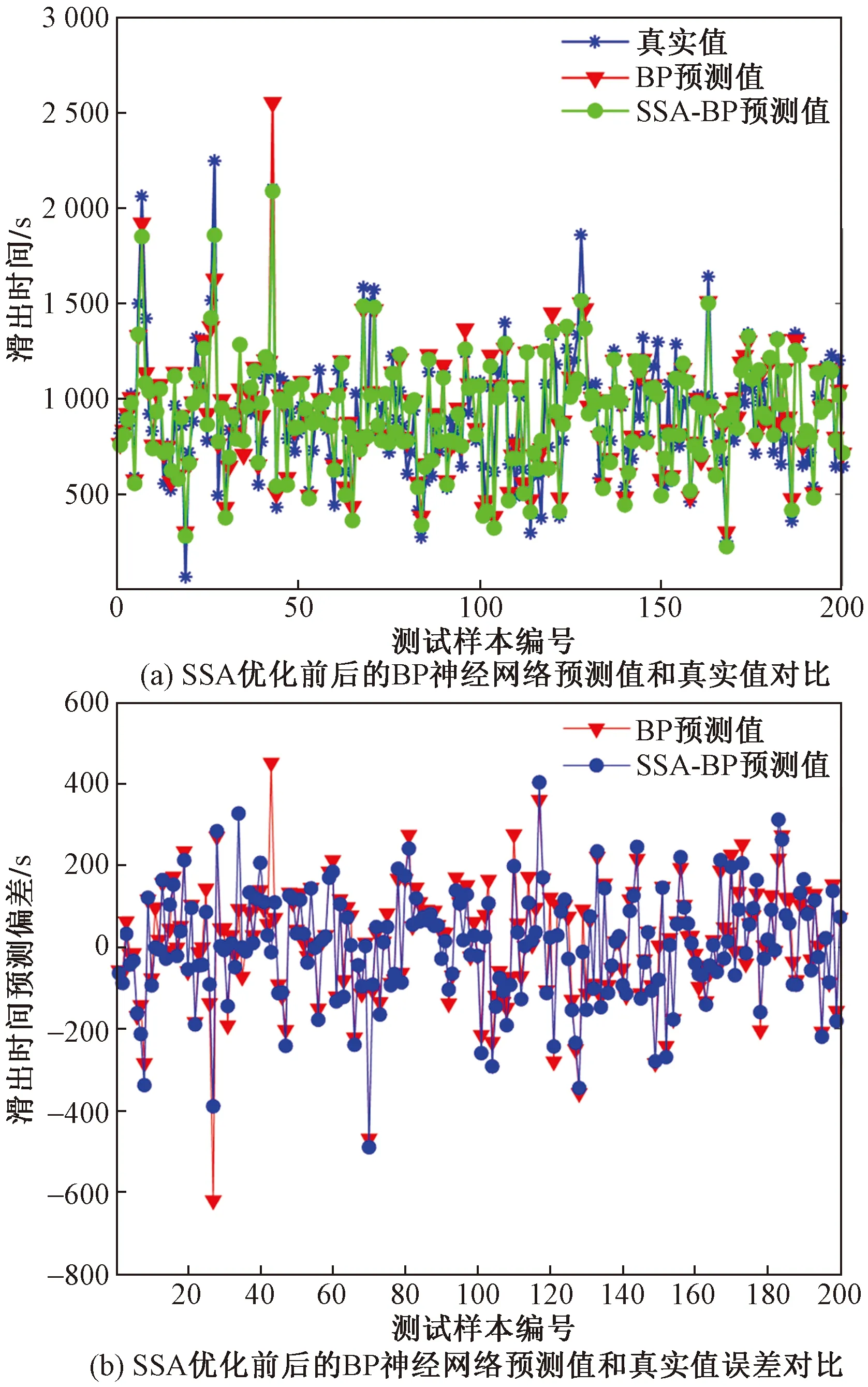
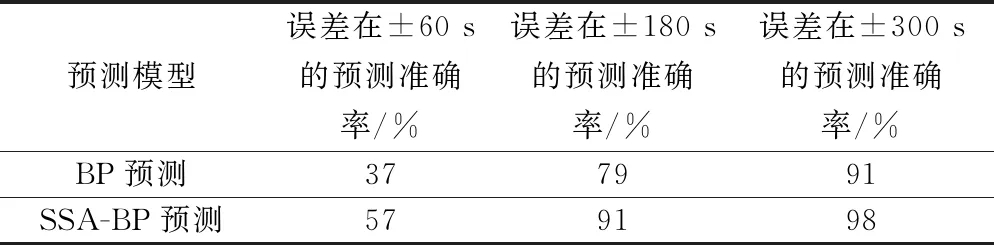

4 结论

