MDA习题课教学模式的建构与应用——以“动能定理的应用”习题课教学为例

王宇辰 胡 正

（1.深圳市龙岗区华中师范大学龙岗附属中学，广东 深圳 518100；2.深圳市龙岗区外国语学校（集团）星河学校，广东 深圳 518100）

1 MDA习题课教学模式的建构

1.1 建构背景

为全面深化课程改革，落实立德树人根本任务，2017年12月，教育部印发了新修订的普通高中课程方案和学科课程标准，把学科核心素养作为确定课程目标、遴选教学内容、设计教学活动的主要依据.［1］物理学科“核心素养”主要包括4个方面，即“物理观念”“科学思维”“科学探究”“科学态度与责任”.2019年，教育部提出要立足全面发展育人目标，构建包括“核心价值、学科素养、关键能力、必备知识”在内的高考考查内容体系.为了能够准确施行新课标、新教材、新评价体系下的物理习题课教学，培养学生基础知识和基本技能的过程中强化对关键能力培养，本文提出了MDA（Model Based Discovery and Application，基于发现与应用的模型，简称MDA）习题课教学模式.

1.2 MDA习题课教学模式解析

基于图1的原型、模型与理论的关系，设计了图2的MDA习题课教学模式，分为4个教学环节并呈现循环的特点.

图1 原型、模型与理论的关系

图2 MDA习题课教学模式

第Ⅰ象限（右上）.MDA习题课教学模式的第1环节是在真实的生活情境中发现原型.情境认知学习理论认为，知识具有情境性，抽象的知识是在与学习情境的有效融合过程中得以不断发展和完善.《普通高中物理课程标准》（2017年版）明确提出：“构建新的物理概念，必须对所观察的现象重新加工，在客观情境中概括事物的共同属性，抽象事物的本质特征.”［1］通过从日常生活以及生产实践中创设使学生熟悉的、真实的情境，让物理学习走向社会，激发起学生对所要探究问题的强烈欲望，使学生感受到学习物理的成功，从而发挥他们的社会责任感，这在物理教学中是非常有意义的.

第Ⅱ象限（右下）.MDA习题课教学模式的第2环节是在实验探究中建构模型.建构主义理论认为，人类均是以自己的经验为基础来建构现实或解释现实，学习是学习者基于自己的知识经验、主动对新信息加工处理、进行有意义知识建构的过程.《普通高中物理课程标准》（2017年版）中对物理学科核心素养进行了水平划分，其中对物理模型建构的5个水平要求如图3所示.

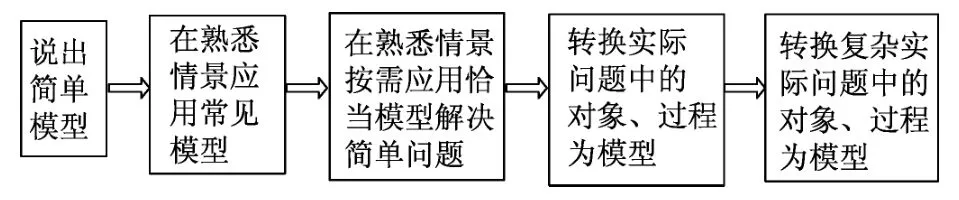
图3 物理模型建构的5个水平要求

从说出到应用再到转换，从熟悉情境到实际问题再到复杂实际问题，课程标准明确地划分了不同水平的物理建模能力，也充分说明培养学生学会建模和应用建模是一个长期的过程，要将物理模型建构渗透到日常的教学中.

第Ⅲ象限（左下）.MDA习题课教学模式的第3环节是在链式问题中深化应用.我国著名的心理学家林崇德教授提出关于思维发展的阶段论.

如图4所示，各种思维形式之间是替代与共存的辩证统一关系.如最初的直观行动思维在个体发展中向着两个方向转化，一是给具体形象思维让位，二是向更高水平的动作逻辑思维发展；对于具体形象思维来说，既是抽象逻辑思维的直接基础，同时也是形象逻辑思维的前期阶段.［2］我们将思维发展阶段论用在实际的习题课教学中，前两个教学环节培养学生直观行动思维和具体形象思维，那么第3个教学环节将在此基础上培养学生的抽象逻辑思维.而链式问题的设置就像思维的“脚手架”，可以帮助学生攀上新的认知结构.解决链式问题可以让学生在千变万化的题目中抓住解决问题的本质，在经历推理、归纳的过程中渗透问题意识和证据意识，培养学生的抽象逻辑思维，从而达到举一反三、以不变应万变.

图4 思维发展模式图

第Ⅳ象限（左上）.MDA习题课教学模式的第4环节是在拓展优化中回归原型.明达和史密斯（Minda&Smith，2002）基于原型理论和样例理论提出了“原型表征+样例记忆”的复合学习策略.这一策略要求个体在学习阶段储存相应的原型信息，对新的刺激的归类就根据它与原型相似性得出.［3］返回原型就是回归到最初情境或是相似的情境中，用直观行动思维、具体形象思维和抽象逻辑思维对建构的模型进行优化拓展，从而实现将所学的物理知识内化为解决问题的物理观念和科学思维.

2 MDA习题课教学模式的教学案例

以新人教版高中物理必修第2册“动能定理的应用”习题课教学为例.

2.1 在生活情境中发现原型

通过播放过山车“第一视角”的惊险刺激视频（图5）来激发学生学习兴趣，选取过山车运动过程中特殊的一段进行研究.

图5 过山车实景图

教师启发学生进行思考：“实际的过山车为了保证乘客的安全，会设置很多安全保障措施，其中车轮与圆环轨道间的安全锁就是其中之一，可以有效地防止过山车运行中发生脱轨.试想：如果没有安全锁，过山车在圆环轨道中运行一定会发生脱轨吗？”

这一问题的设置既联系生活实际，又能激发学生探索欲望，在观察现象基础上提出物理问题，在兴趣的驱动下进行科学探究，帮助学生建立正确的相互作用观.

2.2 在实验探究中建构模型

为了方便探究，把没有安全锁的过山车绕圆环轨道的运动等效成小球在圆环轨道中的运动（图6），让学生经历解决物理问题的基本过程——模型建构.这一建构过程强化物理知识与实践情境的关联，激发学生能动性.

图6 实验模型

如图7所示，将小球从斜面轨道不同高度释放，小球在圆环轨道中的运动会出现3种情况：（1）做完整的圆周运动；（2）沿着圆环轨道滑下；（3）脱离轨道做斜抛运动.通过简单的实验解决了“如果没有安全锁，过山车在圆环轨道中运行一定会发生脱轨吗？”这一问题，通过模型建构强调物理情境与物理概念的关联，同化和顺应学生的物理前概念逐步接近更科学的认知，帮助学生形成扎实的物理观念，并注意让学生在情境中运用规律解释物理现象和解决实际问题，从而提升学生科学思维能力，真正做到以学生为中心.

图7 简化模型

2.3 在链式问题中深化应用

动能定理是高中物理中的核心重点内容之一，许多学生在综合性比较强的复杂情境中往往漏洞百出，本节课将复杂情境抽丝剥茧，由简单问题出发，进行“七步”拓展，逐步引导学生运用动能定理解题，并在习题中总结运用动能定理解题的分析方法和基本步骤.

基于上述建构的基础模型，让学生深入探索小球“脱轨”“不脱轨”所隐含的物理规律，从学生基本认知出发，设置例题：“若小球质量m，圆轨道半径R，不考虑钢球与斜面、圆环间的摩擦，重力加速度g.小球要越过圆环轨道最高点，斜面释放点距水平面的高度应满足怎样条件？”

通过这个问题强调“临界值”的重要性，强化物理知识与实践情境的关联，激发学生能动性.著名心理学家皮亚杰的认知发展理论告诉我们，个体的认知发展是以已有的认知结构为基础，教学要让学生在原有的认知结构基础上建立新的认知结构，必须循序渐进、层层深入.该问题的设置可以唤醒学生对动能定理的基本认知，为建构深度认知做好铺垫.

接下来，在例题基础上设置链式拓展问题，如表1所示.

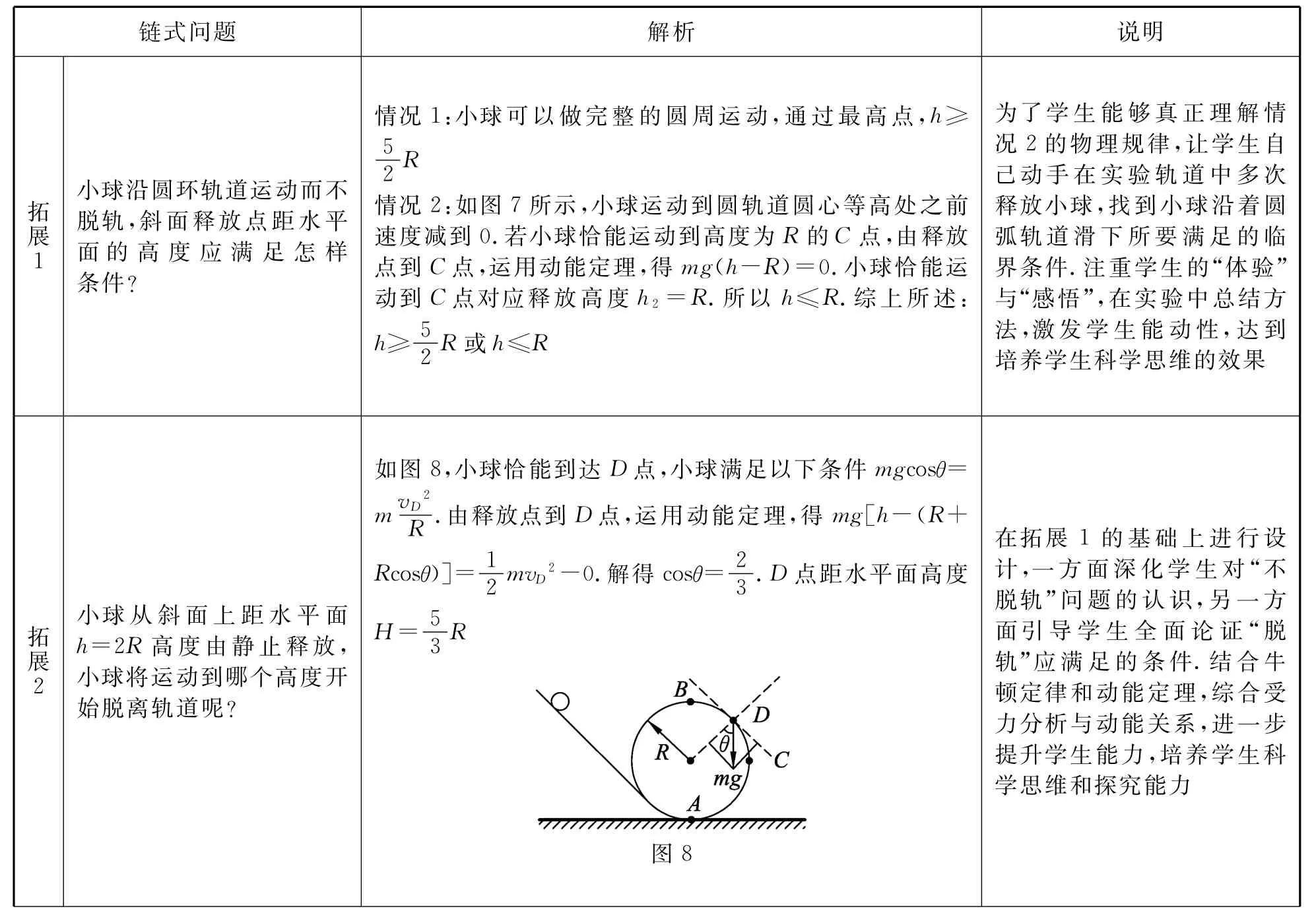
表1 链式拓展问题

续表

2.4 在优化拓展中返回原型

表2 优化拓展中返回原型

3 结束语

如何在习题课教学中使学生的学科核心素养方面获得全面发展？这是每一位一线教育工作者需要深入思考的问题.MDA习题课教学模式是从知识本位转向素养本位的新型习题课教学模式，它强化情境体验，引导学生在真实的生活情境中体验科学探究的过程，形成核心物理知识和观念；它注重模型建构，激发学生的想象力和创造力，培养学生的科学思维；它设置链式问题，鼓励学生发散思维，由浅入深，循序渐进，培养学生应用物理知识和方法解决问题的探究能力；它回归实践应用，在解决问题中渗透科学态度与责任，学会自主迁移并运用于生活情境中，真正做到物理来源于生活并服务于生活.