高考物理压轴题的解题教学要“慢”“导”“探”——以2021年江苏高考物理第15小题为例

曹小云 孙福如

（1.江苏省如东高级中学，江苏 南通 226400；2.如东县丰利中学，江苏 南通 226408）

物理高考从“能力立意”转变为“素养立意”，为了体现高考的选拔功能，压轴题往往条件隐含深，题目信息庞杂，在问题的解决过程中很多学生会出现这样或那样的困惑，从而导致解题困难.其主要原因是这类题的解题教学过程中，各个环节没有落实好，教师越俎代庖、以讲为主，表面上完成了教学任务，其实学生没有审清题目的本质，没有亲身体验解题中发现和推理的思维过程，知其然不知其所以然，遇到新的、复杂一些的情境还是束手无策.为了解决学生“怕生”的问题，在压轴题的教学过程中，要用问题链的方式“将大题化小”“将复杂的问题化为简单问题”，在“慢”导过程中留足思考的时间，为学生把准解题方向和创设机会；在教学过程中要“导”，引导学生把控审题时间、思考方法、探究过程，关注解题程序，引导学生学会思考分析，在“导”的过程中让学生“探”，揭示物理解题的规律与方法.

本文以高三的一次周练压轴题（2021年高考物理江苏卷第15题）为例，开展解题教学，教会学生思考，促进学生学习方式的转变，教学效果较好.

1 试题分析

例题.如图1所示，回旋加速器的圆形匀强磁场区域以O点为圆心，磁感应强度大小为B，加速电压的大小为U、质量为m、电荷量为q的粒子从O附近飘入加速电场，多次加速后粒子经过P点绕O做圆周运动，半径为R，粒子在电场中的加速时间可以忽略.为将粒子引出磁场，在P位置安装一个“静电偏转器”，如图2所示，偏转器的两极板M和N厚度均匀，构成的圆弧形狭缝圆心为Q、圆心角为α，当M、N间加有电压时，狭缝中产生电场强度大小为E的电场，使粒子恰能通过狭缝，粒子在再次被加速前射出磁场，不计M、N间的距离.求：

图1

图2

（1）粒子加速到P点所需要的时间t；

（2）极板N的最大厚度dm；

（3）磁场区域的最大半径Rm.

本题以学生熟悉的回旋加速器为背景，考查其工作原理，突出了理论知识与生产生活实际、现代高科技的紧密联系.引进“静电偏转器”，又增加了思维的难度，考查学生的物理核心素养，实现了高考的选拔功能，是一道体现应用性和创新性的高质量试题.练习后本题的得分率很低，在试题讲评前，笔者充分了解了班级学生的答题情况，梳理出学生的困难点.

（1）信息读取能力、挖掘隐含条件能力不足.学生不能读懂“从O附近飘入”“粒子恰能通过狭缝”等，不能画出粒子的运动轨迹、判断圆心是变化的，不会寻找几何关系等.

（2）不会把大题化小.不能将整题分解为多个小问题思考，各个击破.

（3）思维能力不足.不能从已知条件分析、推理得出新的结论.

（4）运算能力不足.本题因条件多、变化多，找关系式难，且列出的关系式多，找不到运算联系的纽带，运算方向不明.

基于以上问题，教学时需要结合题目的条件，帮助学生理解题目考查的知识点和能力点.在教学中要“导”，即教师由近及远、由易到难地设计启发性问题，引导学生主动探究、分析出合理的解题思路.在“探”的过程中积累解题经验和思维方法.

2 教学过程分析

2.1 引导探究

问题1：本题总体难度较大，虽然一眼望去不能找到解题思路，同学们再次认真审读题目，看能不能找到你熟悉的条件，并以此为突破口？

学生仔细分析，能够发现条件“磁感应强度大小为B，粒子质量为m，电荷量为q，经过P点绕O做半径为R的圆周运动”可作为突破口.

问题2：根据刚才的分析，要求粒子加速到P点所需要的时间还差什么条件？题目中还有哪个条件没有充分利用？

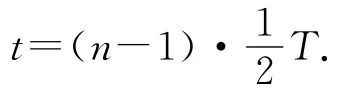
教师：第1问属中等难度，要求学生熟悉回旋加速器的工作原理，知道粒子的运动过程.易错点是求时间时粒子旋转半周期的个数比加速次数少1.

2.2 逐步探究

问题3：第2问极板N的最大厚度与什么因素有关呢？

学生独立思考并小组讨论后，有学生举手要回答.

学生5：跟粒子在磁场中运动的半径有关.N极板不能挡住粒子在磁场中运动的轨迹.

问题4：分析得很好，大家结合定量计算能定性画出粒子运动的轨迹图吗？并分析N板的厚度跟哪几个半径有关？

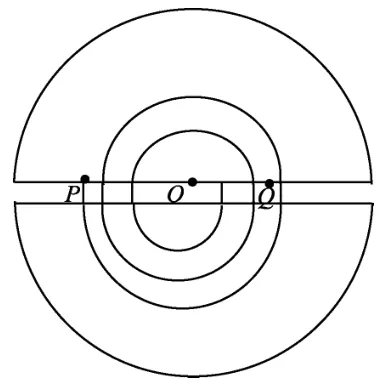
图3

学生7：为了N极板不挡粒子的运动轨迹，所以厚度与rn和r（n-2）有关，N板的最大厚度等于第n次加速后轨迹与第（n-2）次加速后轨迹的间距，即dm=rn-r（n-2）.

学生8：学生7前面分析是对的，但dm的计算是错的，他认为rn和r（n-2）对应的轨迹的圆心在同一点，其实每次加速后半径均有增大，且每次轨迹圆心是不重合的，N板的最大厚度应该是dm=r（n-1）-r（n-2）.

学生9：dm的计算还是错的，由图3可知，（n-2）次加速与（n-1）次加速后的轨迹右侧对齐，dm是这两次轨迹的直径之差，即dm=2［r（n-1）-r（n-2）］.

教师：第2问有一定的难度，解题过程中要求同学们具有恒心和毅力，需要沉着冷静、认真分析，侧重考查同学们的分析与综合、判断与推理的能力.同学们所犯的典型错误是认为圆心在同一点，误认为dm=rn-r（n-2）.

2.3 深入探究

问题5：如图2所示，粒子经过P点后进入“静电偏转器”，粒子的圆周运动半径发生了怎样的变化？说明了什么？

问题6：粒子从“静电偏转器”狭缝的末端E射出，再次进入纯磁场中，同学们试想一想，接下来需要考虑什么问题呢？

学生12：需要考虑粒子做什么运动.由于粒子速度垂直磁场，所以仍然做匀速圆周运动.由于速度大小和磁感应强度大小均没有变化，所以圆周运动的半径仍为R，圆心在O′，轨迹如图4所示.

图4

问题7：对于条件“使粒子恰能通过狭缝，粒子再次被加速前射出磁场”，能想到什么问题？同学们在独立思考的基础上再以小组讨论一下.

学生13：必须找出磁场最大区域的条件，如果磁场区域较大，包围了粒子的轨迹，那么粒子会被再次加速.若磁场区域半径从较大逐渐减小过程中，当以O为圆心的磁场区域边界与粒子的轨迹相切时，为临界情况.切点即离O最远的点在OO′连线的延长线与轨迹的交点F处，此时为恰能将粒子引出磁场的区域.

问题8：根据上面的分析，如何计算磁场区域的最大半径Rm呢？

学生14：如图4可知，Rm=OF=OO′+O′F=OO′+R（OO′怎么求该学生说不出了）.

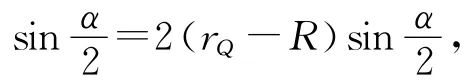
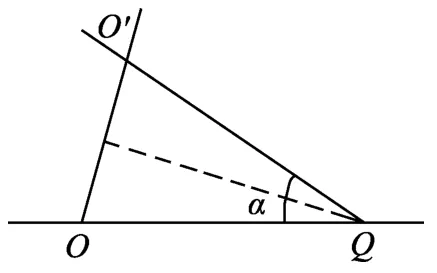
图5

教师：第3问引入了“静电偏转器”，增加了试题的难度.内容上重点考查了粒子在复合场的匀速圆周运动、有界磁场的临界问题及三角形的知识等；能力上将分析与综合能力、判断与推理能力、用数学知识处理物理问题的能力和物理核心素养的考查有机融合在一起.为学生们展现发散性思维、个性素养提供了广阔的空间，这是江苏高考的一大亮点.从本题的学习我们应该体会到：将新问题转化为旧问题、将复杂问题转化为简单问题是解决这类题的关键，探究、分析、判断、推理、建模是解决这类题的必要条件.

3 教学启示

高考物理压轴题的教学，关键有三点：一是思路分析；二是物理规律选择；三是思维方法和运算方法指导.在认真审题的基础上，探讨的解题思路必须符合学生思考的实际，思路要清晰.教学过程中必须暴露学生的思维过程，及时点拨学生的思维和纠正思维的方向，起拨乱反正的作用.运算要写出合理的过程，即使复杂也要善于引导学生进行分析和运算过程指导.为了提高教学效果，主要关注以下几点.

（1）教学采用“慢”“导”“探”的教学策略.在解题教学过程中，必须为学生的思考留足时间、创设空间.教师以学生的思维为起点，从题目的背景、内容、方法、过程及渗透物理思想等出发，通过教师“导”，让学生“慢”思考，使不同的学生会得到不同的观点和思路，都养成善于思考的习惯.给出足够的时间让学生“探”，探出适合自己的解决问题的经验，教师帮助学生确定解决问题的方向，疏通思维阻塞的原因与位置，开阔思维的视野.在“慢”中思考，在“导”中探究，在“探”中提升.

（2）用物理问题链展开教学.高考压轴题往往难度比较大，抽象难懂，学生一眼不能看出解题方法.在教学过程中，可通过设计有价值、有层次的环环相扣的问题链来搭建学生探究新知或解题思路、解题方法的平台，激发学生去学习，引导学生思维参与，促进学生积极思考，体会物理知识点生成过程、物理的基本思维方法，以及物理思考中严谨、理性的科学精神.用问题组织学生讨论，教师应鼓励学生在展示环节上相互质疑、争辩，疑难处教师点拨，使课堂处在动态和不断生成的过程中，引领学生在“误”中“悟”，在“错”中“磋”.教学中充分暴露学生的思维过程，找到打开学生“假懂”这把锁的钥匙.在设计与实施物理问题链教学时，需要从学生思考的角度和符合学生自然的思考脉络去设计问题，把握以关联为逻辑起点、以物理思维为基本依据、以教学功能为定位等3个关键点.

（3）注重认知结构的完善.学生的物理认知结构越完善，物理学习的效果越明显.教师在教学中把握学生的学习起点，在其最近发展区内通过问题导入，由浅入深、由点到面、循序渐进地开展教学，引导学生逐步构建物理知识体系框架，完善物理认识结构，提升物理核心素养.当前乃至以后的高考，更加强调高考物理考查的基础性、综合性、应用性和创新性.特别是综合性，要求对同一层面的知识、能力、素养，能够横向融会贯通，形成完整的知识结构网络；对不同层面的知识、能力、素养，能够纵向融会贯通，形成紧密相连、具备内在逻辑关系的整体.

解题教学过程中，只要我们教师耐心地“导”，帮助学生确定解题问题的方向，疏通思维的障碍，为学生创设思维的空间，让学生“慢”思考，在反思中完善知识体系，在“探”中培养思维的批判性和深刻性，定能使学生对解题思维从无序走向有序，从偶然走向必然，从浅显走向深刻.