利用特征模式分析抑制蝶形缝隙天线系统的带外耦合

李晓瑜， 赵泽宇， 裴立力， 李 莉， 韩国瑞

(山西大学 物理电子工程学院， 山西 太原 030006)

0 引 言

现代无线通信系统(包括5G)的一项应用广泛的无线电接收技术是大规模多输入多输出(Multiple Input Multiple Output， MIMO)技术， 它可以有效提高信道容量和信道鲁棒性. 但是当MIMO天线密集分布时， 天线之间会高度耦合， 产生电磁干扰， 从而降低无线通信系统性能[1]. 因此， MIMO天线间的耦合抑制是一个值得关注的问题.

当MIMO天线工作在多个频段时， 天线的高次谐波会产生杂散辐射， 从而影响天线性能并降低天线效率， 这种现象称为带外干扰[2]. 为了降低这种干扰， 学者们已经提出了多种抑制高次谐波的方法. 第一种方法是引入开路短截线. 文献[3]通过在微带馈线上加载3个开路短截线， 在二次和三次处谐波的反射系数分别提高了25 dB 和15 dB. 文献[4]通过在微带馈线上加载6个开路短截线， 在二次、 三次和四次谐波处的反射系数分别提高了2 dB， 10 dB和14 dB. 第二种方法是使用阶梯阻抗谐振器(Stepped Impedance Resonator， SIR). 文献[5]设计了一种由共面波导馈电的电感耦合阶梯阻抗缝隙天线结构， 在二次、 三次和四次谐波处的反射系数分别提高了23 dB， 15 dB 和2 dB. 文献[6]设计了一种由阶梯阻抗偶极子、 阶梯阻抗谐振器和低通滤波器组成的印刷平面滤波天线. 通过引入阶梯阻抗偶极子取代均匀偶极子， 天线的阻带频率从7.2 GHz扩展至14.0 GHz以上. 第三种方法是引入光子带隙(Photonic Bandgap， PBG)结构. 文献[7]通过将具有十字形或正方形晶格的PBG结构结合到馈电网络中， 天线实现了50%的阻带带宽. 第四种方法是引入缺陷接地结构(Defected Ground Structure， DGS). 文献[8]通过在天线接地板上蚀刻矩形和三角形DGS， 实现了92%的阻带带宽. 文献[9]通过在微带线下方蚀刻两个工字形DGS， 实现了107%的阻带带宽. 第五种方法是引入接地导线. 文献[10]将T形微带中的窄微带线部分和接地的T形导线构成L-C谐振器， 天线实现了85.7% 的阻带带宽. 文献[11]中分别通过将接地面连接的T型、 U型和半蝶形导线插入到缝隙天线中， 天线实现了90.9%的阻带带宽. 上述方法共同的特点就是需要额外引入谐波抑制结构， 增加了整个系统的尺寸和复杂度. 近期, 有学者提出了一种通过特征模式分析抑制高次谐波的新方法[12-13]. 通过在偶极子上加载感性负载， 使双偶极子天线系统的带外互耦降低了12.9 dB， 这种方法不需要改变天线系统的结构， 更加简单直观.

本文采用特征模式分析方法对双蝶形缝隙天线系统进行带外互耦抑制. 在特征模式分析的基础上， 给出天线的带内耦合模式和带外耦合模式， 并给出各模式的电流分布. 选择在带内耦合模式电流密度低而带外耦合模式电流密度高的位置加载容性负载， 降低了天线的带外干扰， 同时保留了天线的带内性能. 仿真测试结果表明， 加载容性负载后， 天线的带外耦合降低了24.5 dB， 而带内性能没有降低. 此外， 本文采用同样的方法对线性排列和二维排列的三单元蝶形缝隙天线系统进行了带外互耦抑制， 仿真结果表明， 天线在加载容性负载后， 在2 GHz 的带外互耦均降低了至少 18 dB.

1 用特征模式理论表示天线互耦

图 1 为一个由中心馈电的二元天线系统， 天线1的馈电端口宽度为lp1， 天线2的馈电端口宽度为lp2.在特征模式理论中， 导体上的感应电流密度J用特征电流Jn展开为

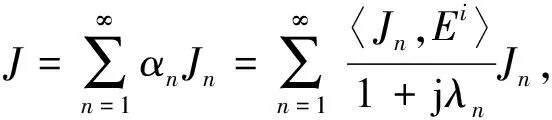
(1)

式中：λn为n阶特征值；Jn为相应的特征电流；αn为Jn的模式激励系数；Ei为激励电场.如果在天线1的馈电端口施加电压V1， 激励电场Ei可用V1沿天线1的馈电端口的分量表示， 则模式激励系数αn可表示为

(2)

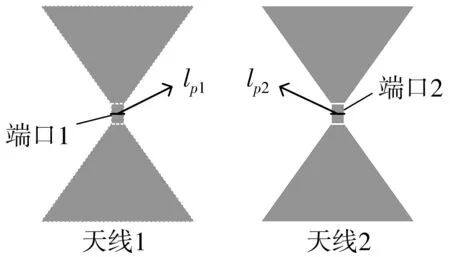
图1 由中心馈电的二元天线系统Fig.1 Two antenna systems fed from the center

此时， 天线1的馈电端口的总电流用n阶模式电流表示为

(3)

天线2的馈电端口的总电流用n阶模式电流表示为

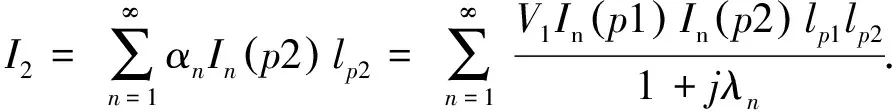
(4)

天线1自导纳是馈电端口的总电流I1与天线1 的馈电端口施加电压V1的比值， 可以用n阶模式自导纳(MSA)的和来表示

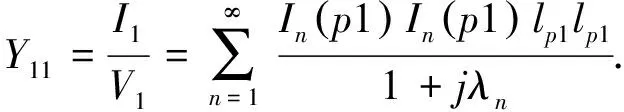
(5)

天线1和天线2之间的互导纳是天线2的馈电端口的总电流I2与天线1的馈电端口施加电压V1的比值， 可以用n阶模式互导纳(MMA)的和来表示

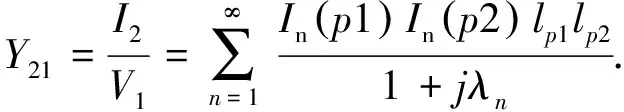
(6)

当天线1的n阶特征电流较弱时， MSA相对较小， 模式对天线1的自导纳贡献较小， 可以忽略不计； 当天线1的n阶特征电流较强时， MSA相对较大， 模式为天线1的主要辐射模式； 当天线1或天线2的n阶特征电流较弱时， MMA相对较小， 模式对互导纳的贡献较小， 可以忽略不计； 当天线1和天线2的n阶特征电流均相对较强时， MMA相对较大， 是产生天线耦合的主要模式.

2 双蝶形缝隙天线系统

图 2 为双蝶形缝隙天线系统结构. 天线采用厚度为1 mm， 相对介电常数为 4.4的FR-4介质板. 介质基板的上表面是与介质基板长宽一致的接地板， 在接地板上对称蚀刻了两个蝶形缝隙， 两个缝隙之间的距离d=75 mm， 如图 2(a) 所示. 介质基板的下表面是两条馈线feed 1和feed 2， 分别为天线1和天线2馈电. feed 1 由长度为l5的锥形微带线和长度为l6的矩形微带线组成， feed 2由长度为l7的锥形微带线和长度为l8的矩形微带线组成， 锥形微带线的宽度均由1.5 mm向 0.2 mm 渐变， 如图 2(b)所示. 表 1 列出了图2双蝶形缝隙天线系统的具体尺寸.

表 1 双蝶形缝隙天线系统的尺寸Tab.1 Dimensions of two bowtie aperture antennas system

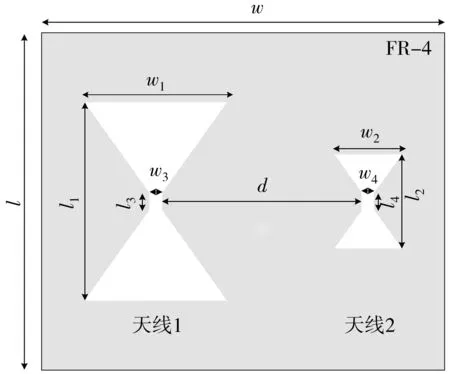
(a) 天线

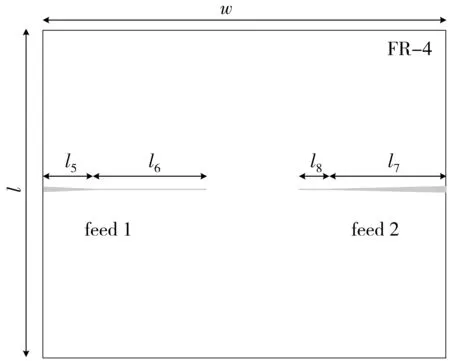
(b) 馈线图2 双蝶形缝隙天线系统结构Fig.2 Structure of two bowtie aperture antennas system

图 3 为双蝶形缝隙天线系统的S参数仿真结果， 天线1的中心频率f1=1 GHz， 天线2的中心频率f2=2 GHz， 天线系统在f2处的带外互耦S12为-25 dB.f2与f1是倍数的关系， 天线通常在谐波频率下才会产生较强的杂散辐射， 对天线的带内性能造成的干扰较大.

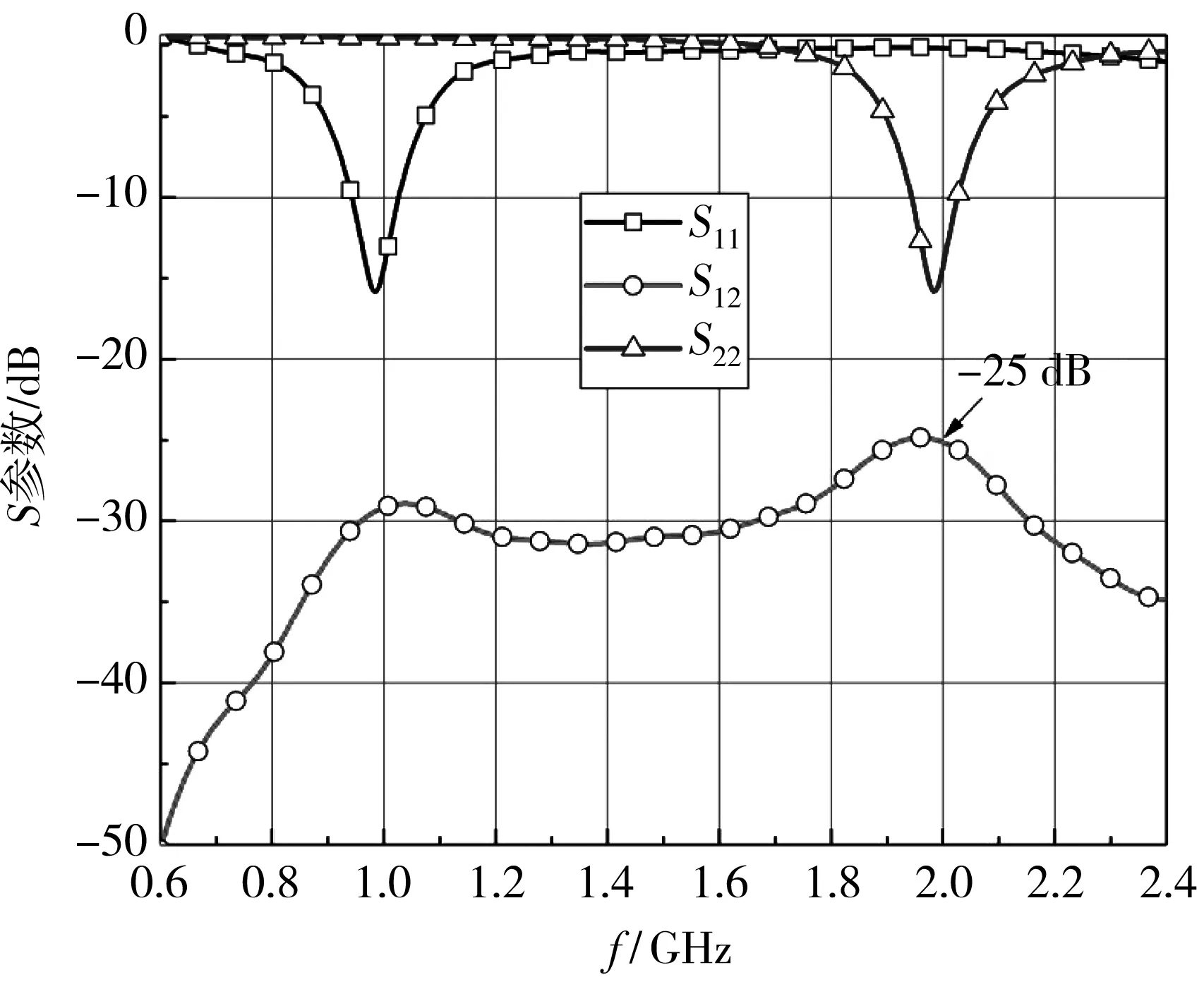
图3 双蝶形缝隙天线系统的S参数Fig.3 S-parameter of two bowtie aperture antennas system

3 双蝶形贴片天线系统的特征模式分析

图 4 为金属板特征电流分布与其同形缝隙特征磁流分布的对应关系. 根据对偶原理， 缝隙天线与其同形贴片的特征值相等， 缝隙天线的特征磁流与其同形贴片的相应特征电流分布类似[13]. 因此， 可以选择双蝶形贴片天线系统作为双蝶形缝隙天线系统的特征模式分析模型.

图4 金属板特征电流分布与其同形缝隙特征磁流分布的对应关系Fig.4 The corresponding relationship between the characteristiccurrent distribution of metal plate and the characteristic magneticcurrent distribution of the same shape aperture

图 5 为双蝶形贴片天线系统在f2的特征电流分布. 图5(a)～(f)为天线的前6个模式. 其中， 模式1和模式4在天线1上的特征电流分布几乎为0， 在天线2上有较强的特征电流分布. 模式3在天线1上有较强的特征电流分布， 在天线2上的特征电流分布几乎为0. 这3个模式产生的天线耦合较小， 可以忽略不计. 模式6在天线1和天线2 上均有较强的特征电流分布， 但在两天线的中心位置特征电流为0. 由于天线在中心馈电， 所以无法激励模式6. 模式2和模式5在天线1和天线2上均有较强的特征电流分布， 是产生天线耦合的主要模式. 模式2是带内辐射模式， 模式5是带外辐射模式.

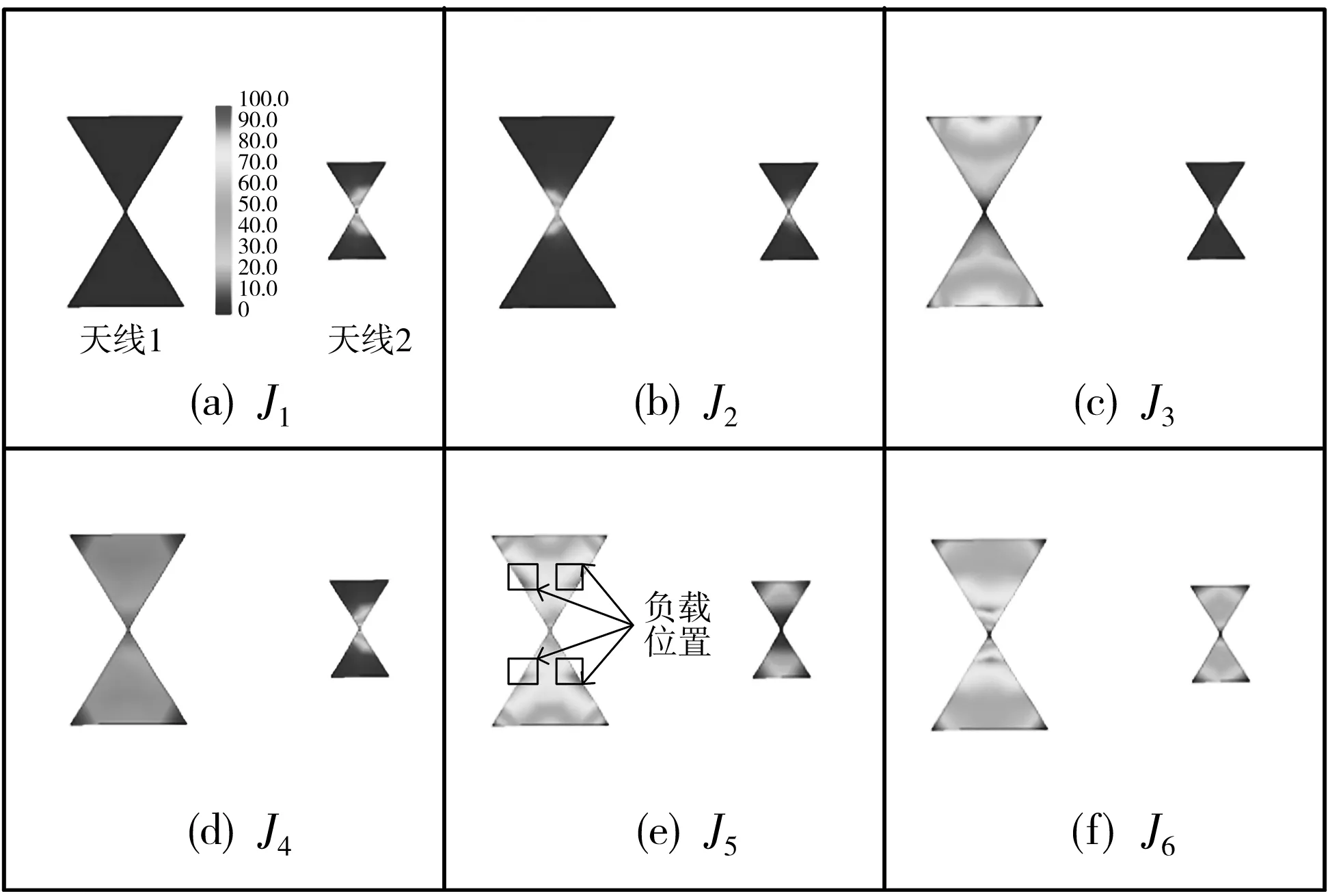
图5 双蝶形贴片天线系统在f2的特征电流分布 (幅度单位为A/m)Fig.5 Eigencurrents of two bowtie plate antennas systemat f2 (magnitude in A/m)

因此， 要降低天线带外耦合， 只需对模式5进行抑制. 为了抑制模式5， 同时对带内辐射产生较小的影响， 将集总负载放置在天线1模式2电流密度低相对应模式5电流密度高的位置. 经过观察分析， 加载负载的位置位于距离蝶形贴片中心大约±0.07λ处， 如图5(e)所示. 在放置负载之后， 表面电流会向着阻抗低的地方流动， 所以在两负载的中间位置刻蚀两条宽度wg=2 mm， 长度lg=13 mm的缝隙. 图 6 为刻蚀两条缝隙后天线系统在f2的特征电流分布， 可以看出刻蚀缝隙之后， 模式5表面电流几乎为0， 模式5被抑制； 而模式2表面电流分布变化不大， 得以保留.

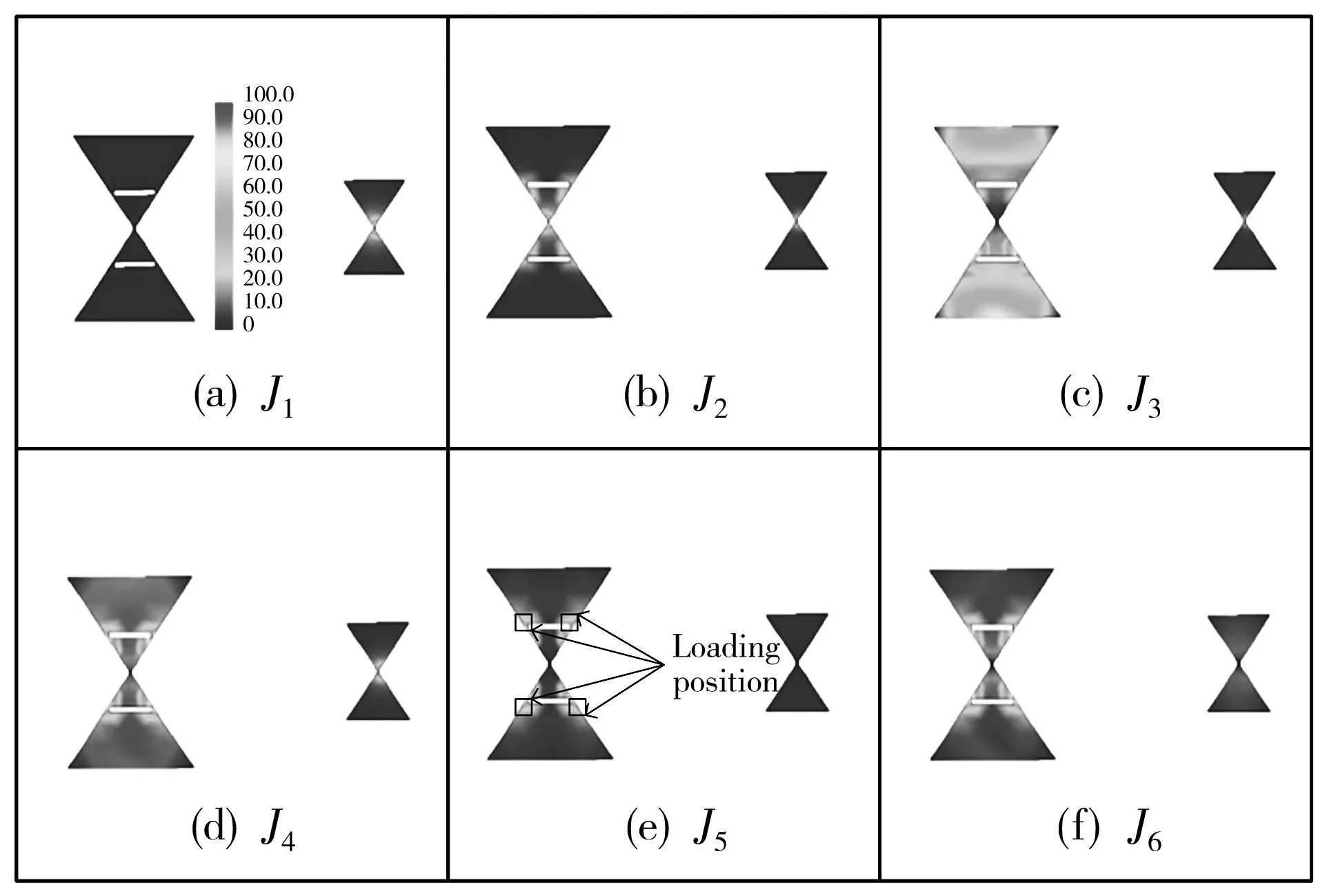
图6 刻蚀两条缝隙后天线系统在f2时的特征电流分布(幅度单位为A/m)Fig.6 Eigencurrents of antenna system at f2 after etchingtwo slot (magnitude in A/m)

4 双蝶形缝隙天线系统进行带外互耦抑制

根据对偶关系， 在缝隙天线中通过加载容性负载实现模式抑制. 图 7 为加载容性负载的双蝶形缝隙天线系统结构.

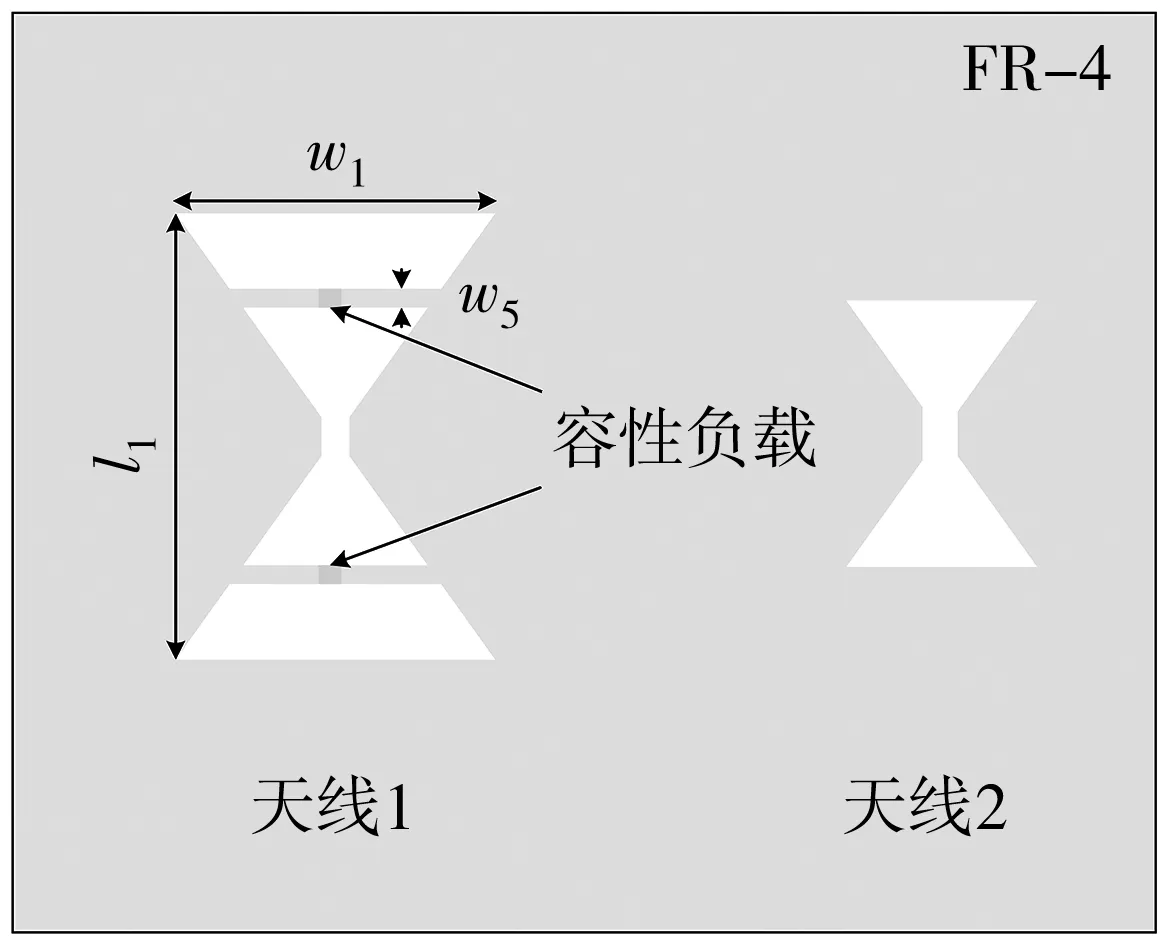
图7 加载容性负载的双蝶形缝隙天线系统结构Fig.7 Structure of two bowtie aperture antennas systemwith capacitive loadings

为了抑制双蝶形缝隙天线系统的带外耦合模式， 在距离天线1中心位置±0.07λ处分别加载了两个宽度w5=0.4 mm的枝节， 每个枝节上连接有一个C=0.5 pF的容性负载. 图 8 为未加载和加载容性负载的双蝶形缝隙天线系统的S参数. 仿真结果表明， 未加载容性负载时， 天线系统在f2处的带外互耦S12为 -25 dB. 加载容性负载之后， 天线系统在f2的带外互耦S12为-43.8 dB， 相比未加载负载时降低了大约 18.8 dB， 实现了带外互耦抑制. 加载容性负载后， 天线1的整体电容增大， 天线1的中心频率f1偏移到了0.7 GHz.

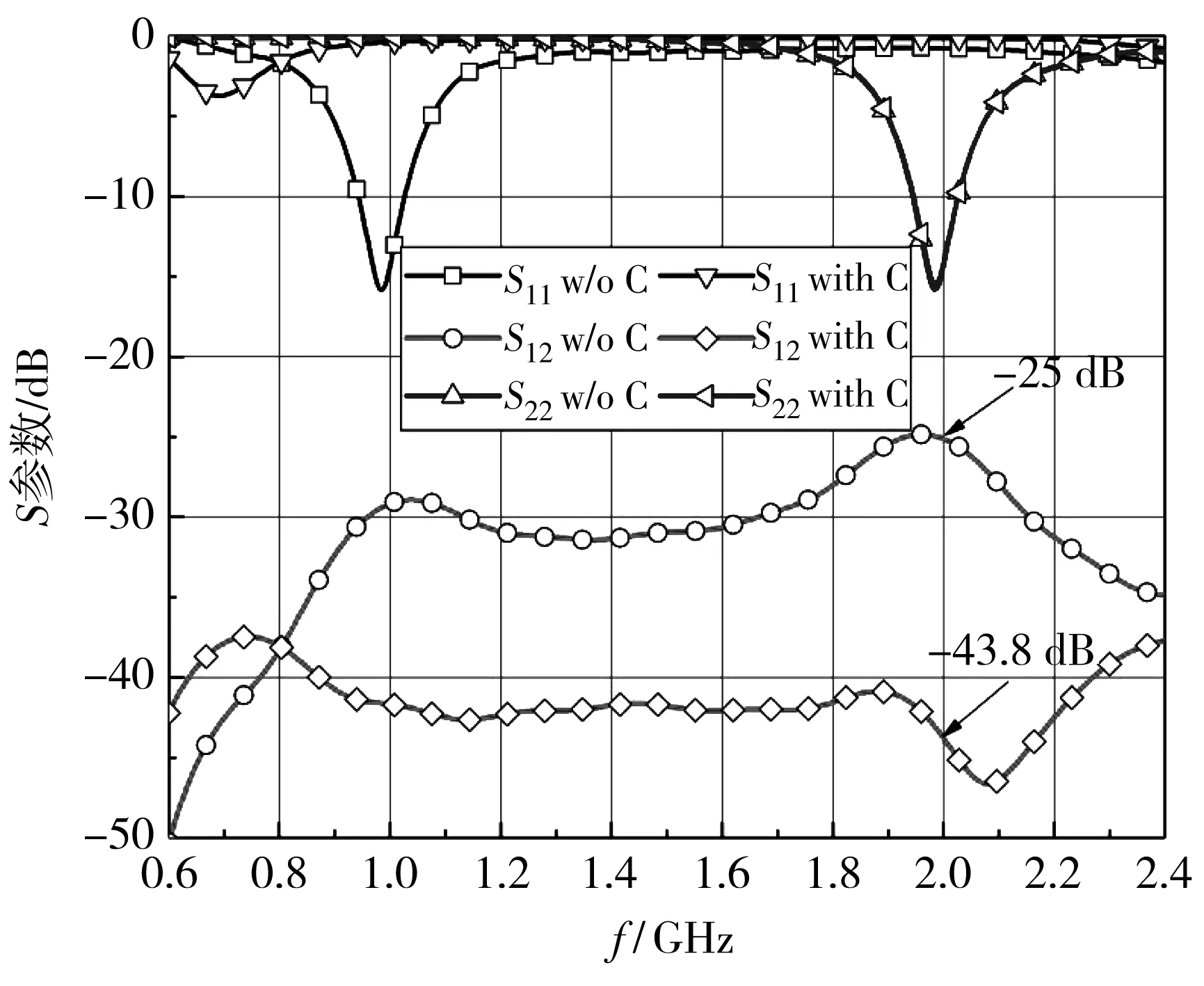
图8 未加载和加载容性负载的双蝶形缝隙天线系统的S参数Fig.8 S-parameter of two bowtie aperture antennas system withand without capacitive loadings

为了使天线1在1 GHz处谐振， 将天线1的尺寸调整为l1=45 mm，w1=26 mm. 图 9 为调整尺寸后双蝶形缝隙天线系统的S参数. 调整尺寸后， 天线1的中心频率f1恢复为1 GHz. 天线系统在f2的带外互耦S12为-49.5 dB.

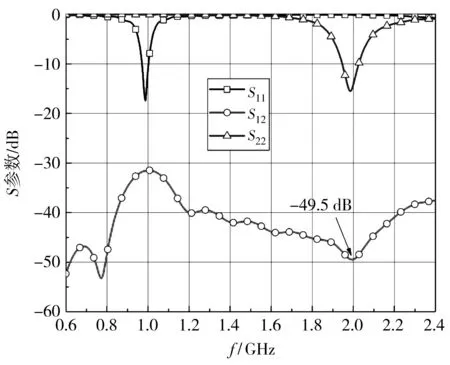
图9 调整尺寸后双蝶形缝隙天线系统的S参数Fig.9 S-parameter of two bowtie aperture antennas systemafter adjusting the size

图 10 为分别加载了不同容性负载的天线系统的S参数.随着容性负载值的增大，f1逐渐向低频移动.加载容性负载后， 天线系统的S12在接近f2处产生了一个陷波点， 随着容性负载值的增大， 该陷波点会不断向低频移动.当C=0.25 pF时，f1=1.1 GHz， 天线系统在f2的S12为 -32.2 dB.当C=0.5 pF时，f1=1.0 GHz， 天线系统在f2的S12为-49.5 dB.当C=0.75 pF时，f1=0.9 GHz， 天线系统在f2的S12为 -32.3 dB.当C=1.0 pF时，f1=0.8 GHz， 天线系统在f2的S12为-27.1 dB. 因此， 最佳负载值为0.5 pF. 相比较未加载容性负载的蝶形缝隙天线系统， 加载0.5 pF电容后，f1不发生变化， 天线系统在f2处的带外互耦S12降低了大约24.5 dB.

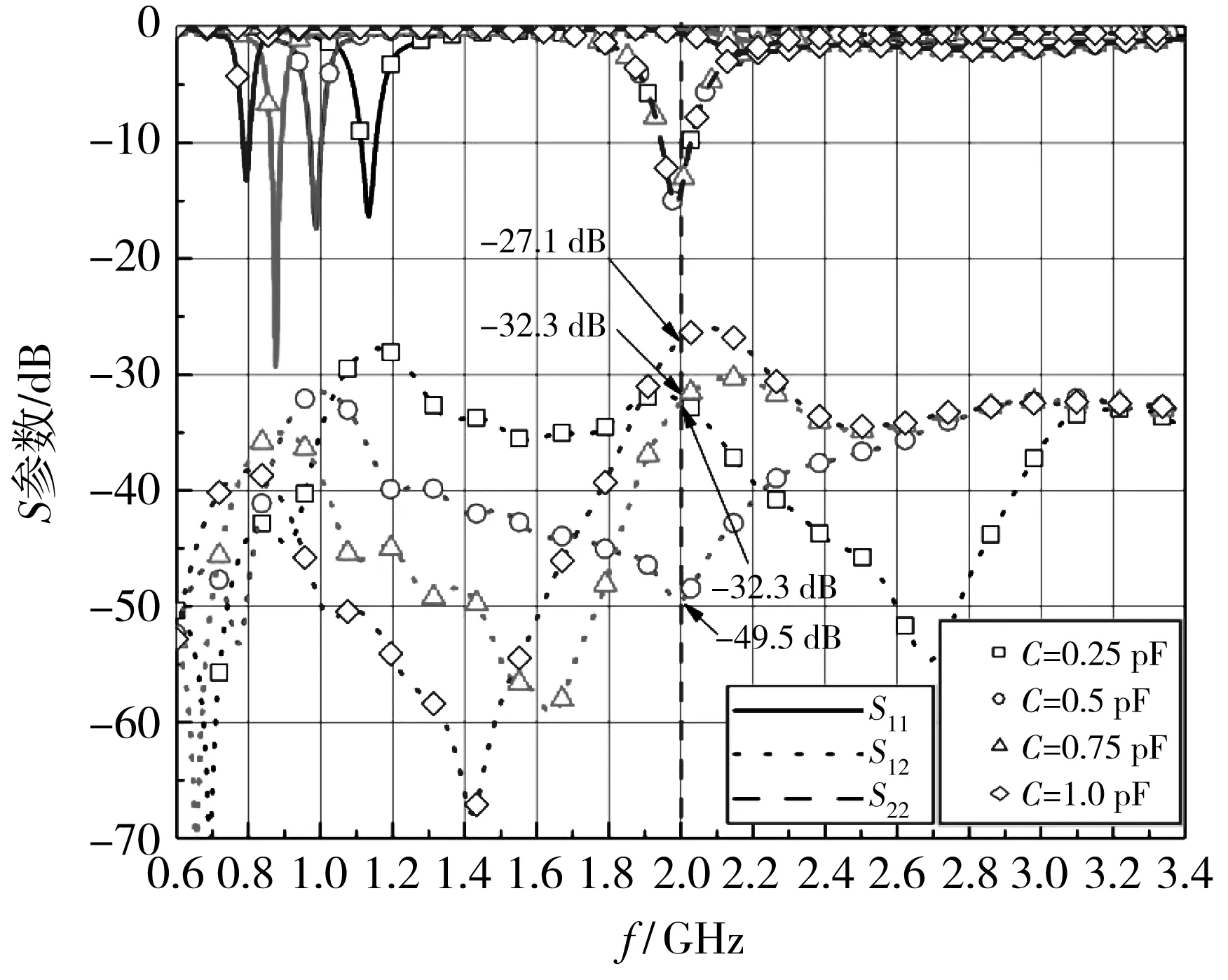
图10 加载不同容性负载的天线系统的S参数Fig.10 S-parameter of antenna system with differentcapacitive loadings

5 线性排列的三单元蝶形缝隙天线系统进行带外互耦抑制

图 11 为线性排列的三单元蝶形缝隙天线系统结构. 其中， 天线1和天线3的中心频率为f2=2 GHz， 天线2的中心频率为f1=1 GHz， 天线1和天线3位于天线2的两侧. 为了对天线2进行边缘馈电， 将天线2的微带馈线进行90°弯折， 如图 11(b) 所示. 图 12 为线性排列的三单元蝶形缝隙天线系统S参数的仿真结果. 此时， 天线1与天线2在f2处的带外互耦S12为-25.4 dB， 天线2与天线3在f2处的带外互耦S23为-26.3 dB.

aperture antennas system

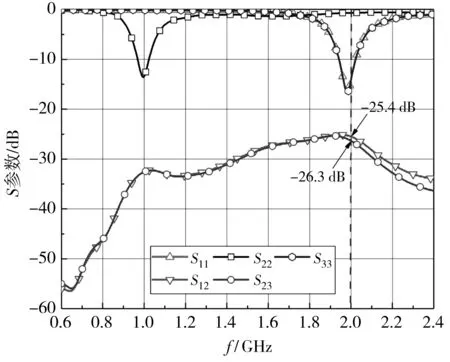
图12 线性排列的三单元蝶形缝隙天线系统的S参数Fig.12 S-parameter of linearly arranged three-unitbowtie aperture antennas system

根据前述方法， 对线性分布的三单元蝶形缝隙天线系统加载容性负载进行解耦. 图 13 为加载容性负载的线性分布的三单元蝶形缝隙天线系统的S参数.

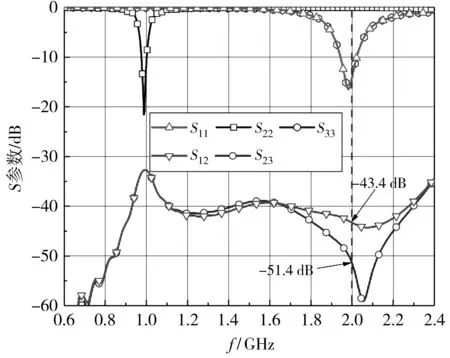
图13 加载容性负载的线性排列的三单元蝶形缝隙天线系统的S参数Fig.13 S-parameter of linearly arranged three-unit bowtieaperture antennas system with capacitive loadings

在天线2上加载电容以及做相应的调整之后， 天线1与天线2在f2处的带外互耦S12为 -43.4 dB， 相比较未加载负载时降低了 18 dB； 天线2与天线3在f2处的带外互耦S23为 51.4 dB， 相比较未加载负载时降低了25.1 dB.

6 二维排列的三单元蝶形缝隙天线系统进行带外互耦抑制

图 14 为二维排列的三单元蝶形缝隙天线系统结构. 其中， 天线2的中心频率为f1=1 GHz， 天线1和天线3的中心频率为f2=2 GHz. 天线1和天线2水平方向线性分布， 天线之间的距离d=75 mm， 天线2和天线3垂直方向线性分布， 天线之间的距离g=75 mm. 图 15 为二维排列的三单元蝶形缝隙天线系统S参数的仿真结果.此时， 天线1与天线2在f2处的带外互耦S12为 -25.1 dB， 天线2与天线3在f2处的带外互耦S23为-25.5 dB.

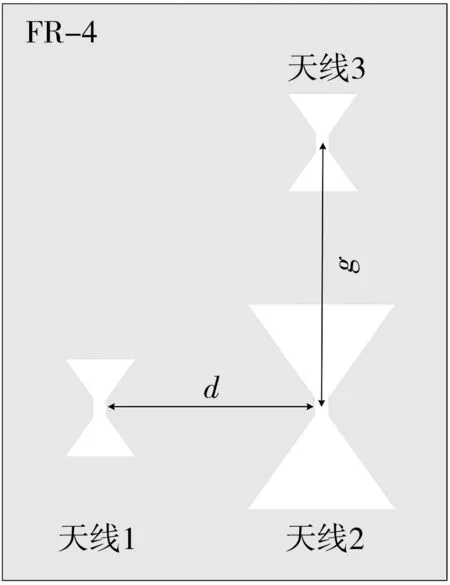
(a) 天线(b) 馈线图14 二维排列的三单元蝶形缝隙天线系统结构Fig.14 Structure of two-dimensional three-unit bowtieaperture antennas system

图15 二维排列的三单元蝶形缝隙天线系统的S参数Fig.15 S-parameter of two-dimensional three-unit bowtieaperture antennas system

同样， 二维分布的三单元蝶形缝隙天线系统也依据前述的方法通过加载电容进行带外互耦抑制. 图 16 为加载容性负载的线性分布的三单元蝶形缝隙天线系统的S参数. 在天线2上加载电容以及做相应的调整之后， 天线1与天线2在f2处的带外互耦S12为-51.2 dB， 相比较未加载负载时降低了26.1 dB； 天线2与天线3在f2处的带外互耦S23为-67.4 dB， 相比较未加载负载时降低了41.9 dB.

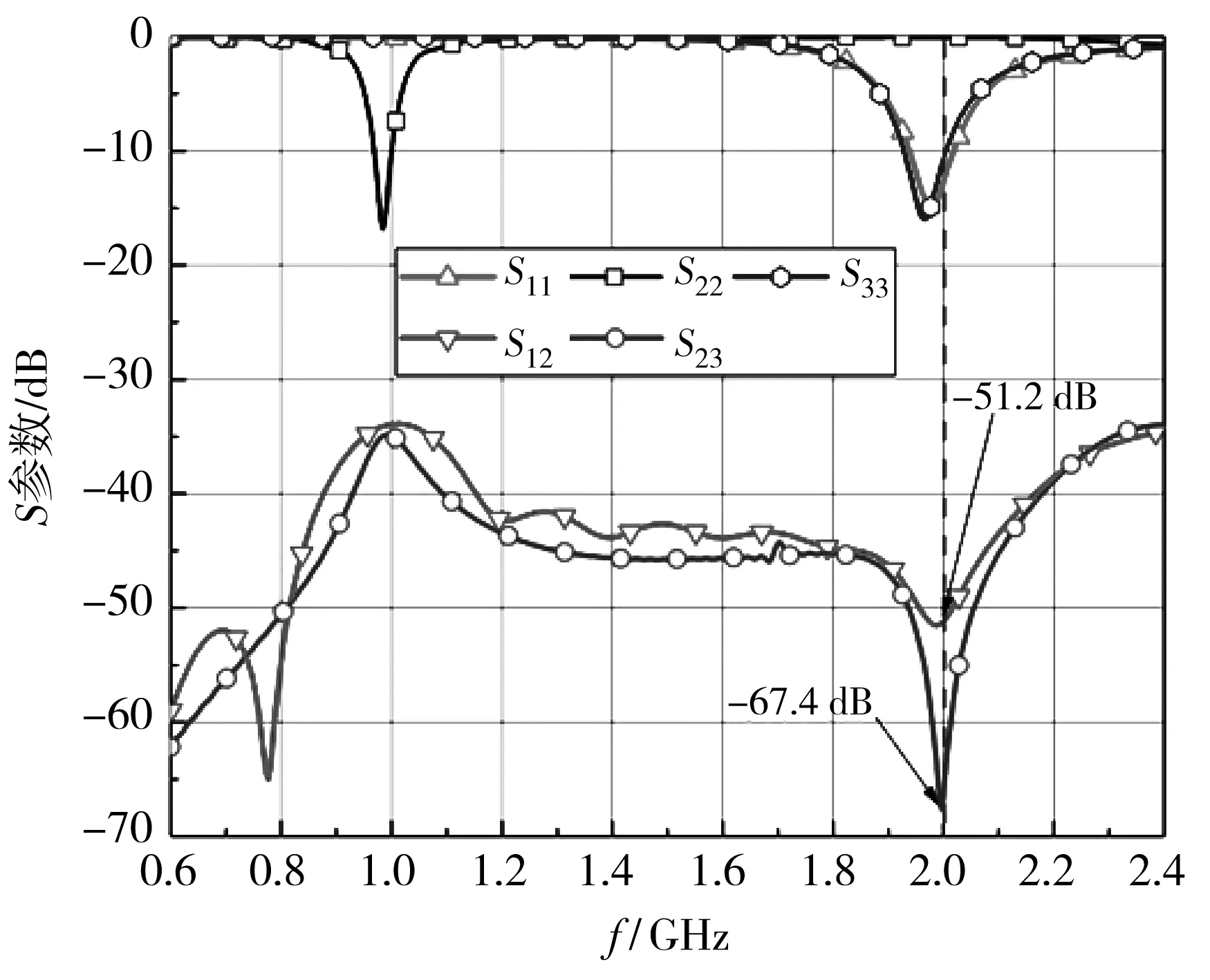
图16 加载容性负载的二维排列的三单元蝶形缝隙天线系统的S参数Fig.16 S-parameter of two-dimensional three-unit bowtie apertureantennas system with capacitive loadings

7 双蝶形缝隙天线系统的仿真和测量结果

图 17 为加载容性负载的双蝶形缝隙天线系统的加工实物图. 天线系统的整体尺寸为 174 mm×87 mm×1 mm. 图17(a)为天线正面图， 在接地面上刻蚀了两个蝶形缝隙， 天线1上焊接了两个0.5 pF的贴片电容(C0603， 容差为0.25 pF ). 图17(b)为天线背面图， 在天线的背面印刷有两条锥形微带线， 微带线的一侧与SMA接口相连.

system with capacitive loadings

图 18 为加载容性负载的双蝶形缝隙天线系统的仿真和测量结果. 仿真结果中， 天线1的中心频率f1=1 GHz， 在f2处的带外互耦S12为 -49.5 dB. 而测量结果中， 天线1的中心频率f1=1.1 GHz， 在f2处的带外互耦S12为-35 dB. 天线1测量的中心频率较仿真结果向高频偏移了0.1 GHz， 主要是焊接的贴片电容的容差导致的. 通过将测量结果与图 10 中分别加载了不同容性负载的天线系统的仿真结果对比， 发现测量结果与加载0.25 pF容性负载的天线系统的仿真结果基本一致， 这说明焊接电容的实际值为0.25 pF， 并不是标称的0.5 pF.

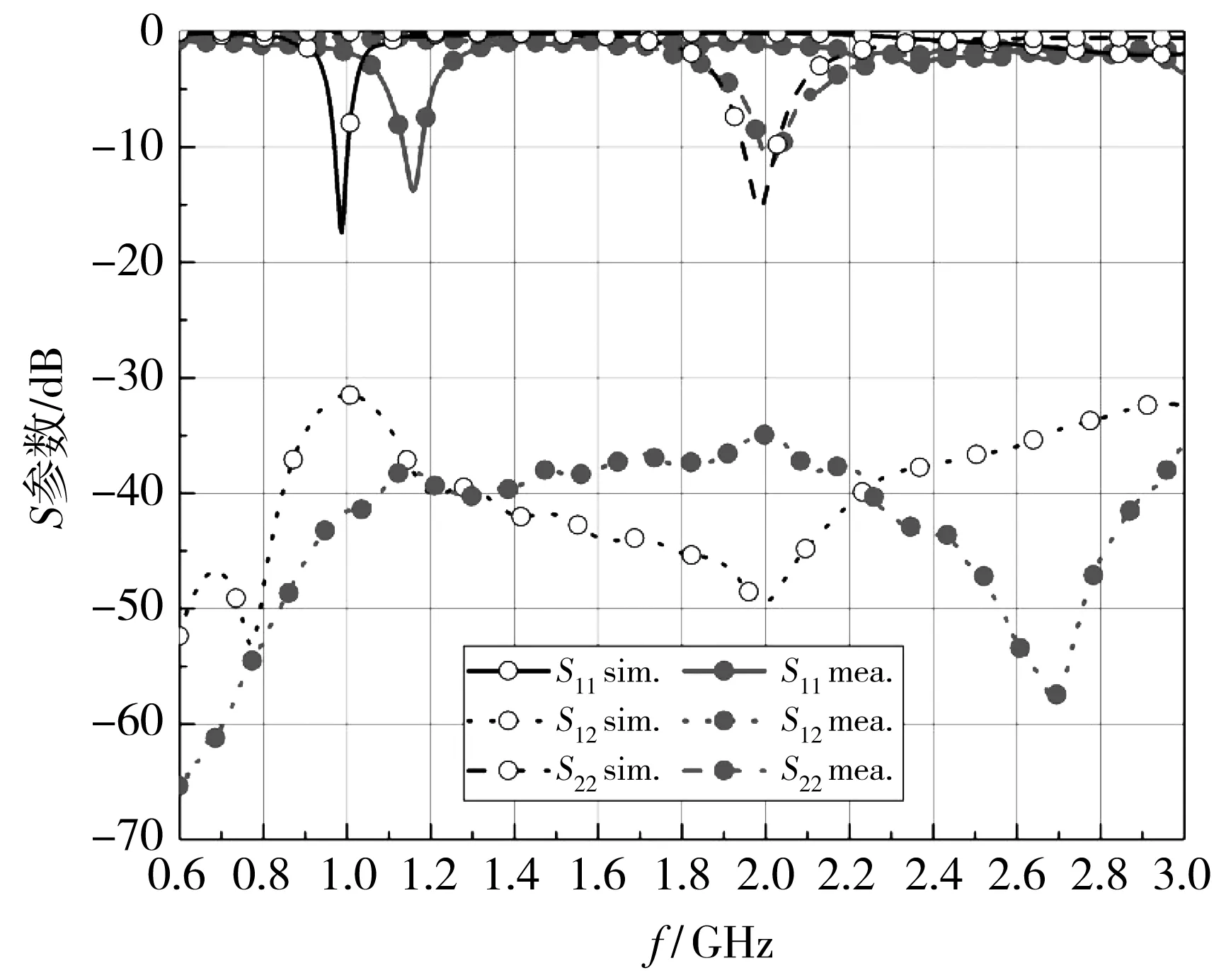
图18 加载容性负载的双蝶形缝隙天线系统的仿真和测量结果Fig.18 Simulated and measured result of two bowtie apertureantennas system with capacitive loadings

图 19 为未加载和加载容性负载的天线1在f1=1 GHz的远场辐射方向图. 可以看出， E面方向图近似为“8”字形， H面方向图为圆形， 呈现较好的全向辐射特性. 未加载和加载容性负载的天线1的辐射图在f1=1 GHz几乎无差异， 因此， 该缝隙天线在抑制带外互耦的同时较完整地保留了天线1的带内辐射性能.

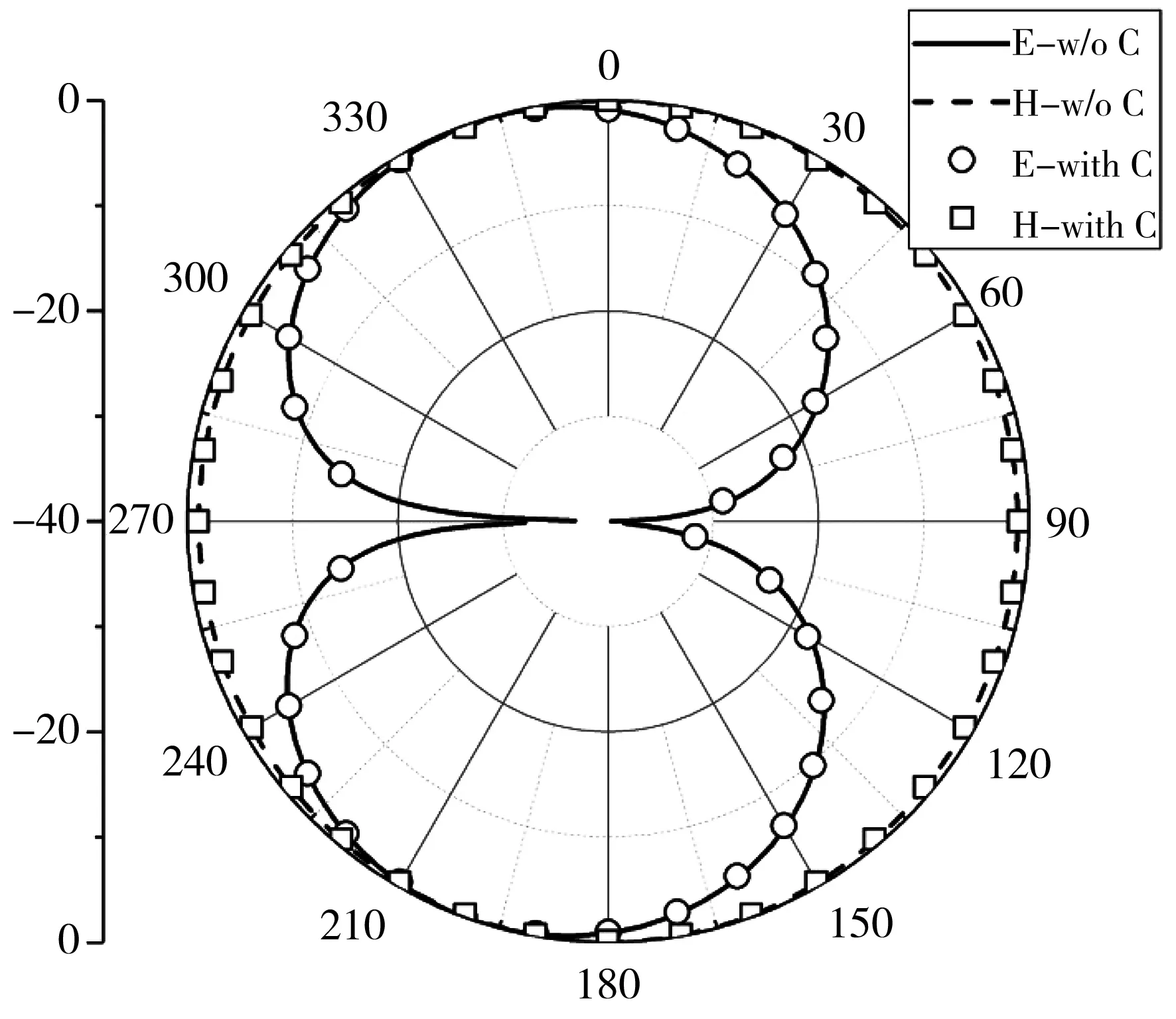
图19 未加载和加载容性负载的天线1在f1=1 GHz的远场辐射方向图Fig.19 Far-field radiation pattern of antenna 1 with andwithout capacitive loadings at f1=1 GHz

8 结 论

本文采用特征模式分析方法对中心频率分别为1 GHz(带内)和2 GHz(带外)的双蝶形缝隙天线系统进行了带外互耦抑制. 对缝隙天线系统进行特征模式分析， 区分天线的带内耦合模式和带外耦合模式. 通过在蝶形缝隙上加载容性负载， 抑制了天线的带外耦合模式， 而保留了带内耦合模式. 仿真和测试结果表明， 天线在加载容性负载后在 2 GHz 的带外耦合降低了大约24.5 dB； 而在 1 GHz 的S参数和远场辐射方向图在加载负载前后变化不大， 保留了天线的带内性能. 此外， 本文还对线性排列和二维排列的三单元蝶形缝隙天线系统进行了仿真分析， 仿真结果表明， 当蝶形缝隙天线线性排列和二维排列时， 加载电容进行带外互耦抑制的方法依旧有效.