蝶形弹簧载荷特性有限元分析法探讨

陈黄发，严皓，朱建华

（广汽研究院动力总成技术研发中心，广东 广州 511434）

1 引言

近年来在轿车和轻型载货汽车上广泛采用的一种蝶形弹簧结构，与压盘是以整个圆周接触，使得压力分布趋于均匀，并且由于具有非线性弹性特性，故能在从动盘摩擦片磨损后仍能可靠稳定地传递设计的转矩。蝶形弹簧是一种对称零件，平衡性好，在高速下其压紧力降低很少，而周向布置弹簧，因受离心力作用会产生横向挠曲，弹簧由于会严重鼓出而降低对压盘的压紧力，从而引起传递转矩降低，导致产品性能无法保证。因此蝶形弹簧载荷特性对保证产品性能极为重要，常见载荷特性计算方法有（A-L法）和（Γ法）[1][2]。本文以普通蝶形弹簧为研究对象，建立蝶形弹簧三维模型，对模型开展有限元分析，通过数值分析和运算得到一条与工厂试验值比较接近的蝶形弹簧有限元分析载荷特性曲线[3]，为实际生产及设计提供数值仿真验证。通过对蝶形弹簧载荷过程工况进行有限元分析，得到蝶形弹簧应力应变数值情况[4]，并进行数值拟合，得到蝶形弹簧的载荷特性曲线。其结果可为蝶形弹簧改进设计及制造加工[5]提供一定的理论依据，并兼顾安全性校核[4]。

2 普通蝶形弹簧

普通蝶形弹簧，简称蝶形弹簧或碟簧。蝶形弹簧（图1）形状像一个没有底的宽边碟子，截面为截圆锥壳形。在上下端面的外径D与内径d处承受轴向载荷F时，其截面的锥底角ɑ减小，使弹簧产生轴向变形λ。蝶形弹簧的主要特点：（1）轴向尺寸紧凑径向尺寸较大，适用于轴向空间小径向空间大承载能力大的场合。（2）具有变刚度的弹性特性，改变高厚比可得到三种不同类型的弹簧特性适用不同工作需求。（3）变形能较大，具有较好的缓冲减振能力，还可以利用各层碟簧片之间的摩擦作用缓冲冲击，衰减振动的阻尼效果。碟簧在重型锻压机械、冶金矿山机械、起重运输机械、车辆弹性悬架、阀门压力控制装置、安全阀压紧弹簧、夹具与机床夹紧机构等领域应用日益广泛。

图1 普通蝶形弹簧结构

3 蝶形弹簧的载荷-变形计算

（A-L法）[1]中采用的假设：（1）在轴向载荷F的作用下，蝶形弹簧的矩形子午截面只是绕中心锥面的某一中性点O（又名翻转中心点）转动一个转角 ψ，而矩形截面本身并没有变形。（2）蝶形弹簧受载时，其载荷和支承反力都是均匀地分布在内圆周和外圆周上。（3）蝶形弹簧的初始锥底角ɑ较小，受载变形时，蝶形弹簧的转角ψ与变形量λ之间的关系是线性的。（4）蝶形弹簧的材料是各向同性的线弹性体，具有完全弹性，其应力与应变关系是符合胡克定律，在卸载后没有塑性变形。（5）蝶形弹簧在制造过程中由于热处理、喷丸、强压处理后所产生的残余内应力未加考虑。（6）受载变形时，蝶形弹簧与上下支承面之间的滑动摩擦未加考虑。（7）受载变形时，蝶形弹簧与两个支承面的接触点位置仍然保持不变，对支承环面圆角半径的影响未加考虑。图2 中取蝶形弹簧的圆锥面母线方向为径向（初始锥底角 ɑ很小），在纸面上垂直于圆锥母线方向为切向。将子午截面中的中性点O取为坐标原点，并取过O点沿中心锥面向外圆周方向的X坐标轴为正，过O点垂直于中心锥面向下表面的Y坐标为正。则当截面上x值为正时，在分析中的σt为正（拉应力），当截面上Y值为正时，分析中的σt为正（拉应力）。

图2 蝶形弹簧受载变形分析简图

根据假设（2），通过对蝶形弹簧的拉、压变形及弯曲变形进行分析推导出碟簧的载荷-变形公式。图3，载荷和支承反力都是均匀分布在内圆周和外圆周上，在扇形微元dθ的内外圆周上的均布载荷均为Fdθ/2π。于是，作用在扇形微元dθ上的外力矩。

外力矩M与径向内力矩Mr相互平衡。于是M=Mr的平衡条件：

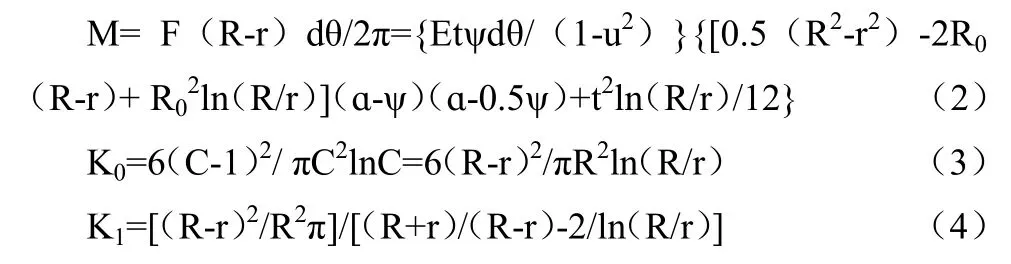
在实际常采用的外内径比C=1.2-2范围内，计算系数中K1稍大于K0，两者仅相差0.72%，因此取K1=K0则蝶形弹簧的载荷-变形公式如下：

图3 扇形微元dθ的力矩平衡

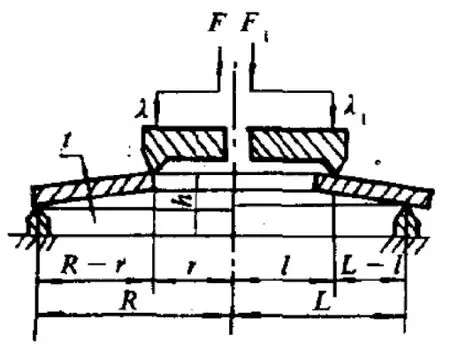
图4 蝶形弹簧受力简图

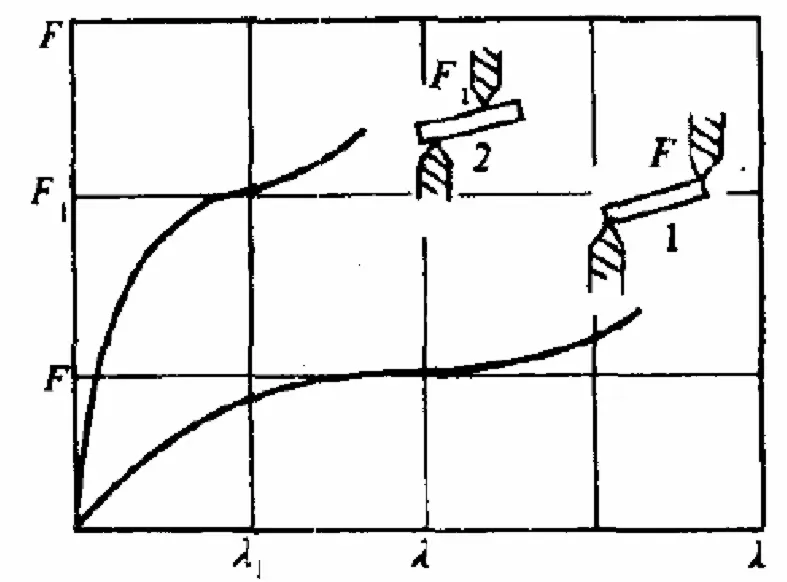
图5 载荷-变形特性比较

4 蝶形弹簧的载荷-变形有限元分析

4.1 应用CATIA建立蝶形弹簧三维模型

蝶簧厚度：2.0mm

碟簧外径：35.5mm

碟簧内径：18.3mm

内锥高：2.8mm

材料弹簧钢：E=206000MPa，u=0.3

图6 蝶形弹簧三维模型

4.2 网格划分

运用Hypermesh划分网格，网格类型为六面体网格，节点34200，单元25992。

图7 蝶形弹簧网格划分

4.3 蝶形弹簧CAE载荷条件[6][7]

将模型导入到Hypermesh，设置蝶形弹簧为六面体网格，材料弹性模量206000MPa,泊松比0.3。边界条件：在碟簧支承圆圈周围节点上约束X方向和Z方向的平移，约束绕Y轴和Z轴的转动，其余各处均可沿Y、Z方向移动。载荷和约束形式与实际形式完全相同，为模拟蝶形弹簧变形全过程，在蝶形弹簧钢性节点RP-2或凸台，沿Z轴负向施加＞0.75h，即施加＞2.1mm的位移载荷。

图8 蝶形弹簧载荷

4.4 蝶形弹簧压紧过程Abaqus求解

将网格划分材料属性及边界条件设置好的模型导入Abaqus中，设置为大变形非线性求解，分析设置为1个载荷步，20个子步进行求解。

图9 蝶形弹簧分析结果

4.5 碟簧特性曲线对比

提取载荷和变形量仿真数据及理论计算[8]绘制图10曲线，纵坐标为载F（N），横坐标为变形量（mm）。

图10 理论计算与有限元仿真特性曲线

由以上对比曲线可以看出：A-L法与有限元法在δ/h＜0.5内，两者的误差为0.9%，误差较小，两曲线基本吻合。随着δ增大误差也逐渐增大，这是由于A-L法计算没有考虑结构非线性及大变形因素。

5 结束语

（1）有限元法对蝶形弹簧的载荷特性曲线分析是合理可行的，而且可以取得较高的精度对改进设计及制造加工有一定的指导作用。

（2）A-L法欠缺考虑大变形过程材料的局部塑性屈服，使得计算数值偏高。

（3）应用有限元法除了可以分析蝶形弹簧的载荷特性曲线，还可以分析蝶形弹簧的应力分布状况，对安全性设计有一定的参考价值。