无人机双机空战对抗侧向机动路径规划*

孙丰础，甘旭升

（空军工程大学 空管领航学院，陕西 西安 710051）

0 引言

空战对抗是现代作战中夺取制空权的主要作战样式，对掌控空中态势发展，达成战术意图具有重要意义。近年来，无人机技术虽得到快速发展，军事装备的无人化程度越来越高，但空战对抗领域仍是有人机的舞台，无人机还远无法达到空战对抗的性能要求。空战战术决策是空战过程中的关键核心［1］。由于无人机自主决策能力的不足，对于复杂的空中态势认知能力欠缺，使得其在空战对抗中往往只能落入下风，难以达成战术目的。但无人机替代有人机执行空战任务是未来必然趋势，将极大丰富空中作战样式，颠覆空战场面貌。早在2016年6 月，人工智能ALPHA 就在空战模拟实验室中以100% 的概率战胜了空战专家、美军退役上校Gene Leep［2］。虽然还只是模拟试验，但已足够验证算法的有效性，离试飞验证和实战检验相差不远。

国内外对无人机空战问题展开了大量研究，基于 智 能 算 法［3-4］、神 经 网 络［5-6］、专 家 系 统［7］、博 弈论［8-9］、贝叶斯网络理论［10-11］等算法是当前实现无人机自主机动决策的主要方法。文献［5］提出一种基于深度神经网络的强化学习方法，通过对敌方距离、速度、角度的态势判断决定我方采取的机动方式。文献［6］通过启发式因子对神经网络进行改进，通过对空战机动的学习训练实现对抗中的机动。但基于神经网络或其改进型的算法都需要借助于训练库，训练库的获取和质量会影响算法的效果。文献［12］提出一种BAS-TIMS 算法，可在一对一对抗中形成一定态势优势。文献［13］则是引入了博弈论的思想，通过敌方可能采取的机动动作计算己方最佳的机动策略，以毁伤概率最大化的原则作为机动选择依据。使用专家系统和贝叶斯网络理论能够实现空战决策机动，但存在决策效率不够高的问题。文献［14］则是将遗传算法和强化学习算法相结合，可实现无人机一对一对抗下的机动决策。上述的各类文献中，大多是单机空战对抗，不涉及态势的判断和目标分配的问题，使用会存在一定的局限性。文献［15］对多机空战进行了研究，可实现二对一对抗中的协同决策，但主要对抗领域为近距对抗，未考虑敌电子干扰作用。

双机编队是空中作战最基本的作战单元，大量攻防战术均可通过长僚机之间的配合实现，更是大规模集群作战的基础，而对抗空战则是夺取局部制空权的主要作战样式。因此，研究无人机二对二模式下的对抗空战技术具有较强的现实意义。本文主要对无人机中距对抗下的二对二对抗环境进行研究，基于A-star 算法设计无人机侧向机动“咬尾”路径，规避敌机火控雷达锁定和干扰吊舱干扰，在机动途中按照优先形成对抗优势的原则展开双机协同和目标分配，尽早构成武器发射条件。

1 侧向机动威胁模型

无人机在于敌机对抗过程中可能受到两方面的威胁，一是火控雷达的锁定，二是电子干扰吊舱的干扰。无人机一旦被火控雷达锁定就会陷入及其被动的状况，需要立即采取大载荷机动动作，逃出火控雷达的照射范围。火控雷达的照射范围一般在机身前向一定角度范围内。无人机进入敌机电子干扰范围内时，自身的雷达信号接收将会受到影响，会出现目标丢失、多目标闪现、位置漂移、假信号等现象。因此，无人机在电子干扰范围内时，难以进行正确的态势判断，空空导弹的命中率也会显著下降。论文在进行无人机的侧向机动决策算法设计时充分考虑了敌机的火控雷达和电子干扰吊舱作用范围，如图1 所示。

图1 敌机威胁态势图Fig.1 Enemy threat situation map

无人机是否进入敌机的威胁范围内主要通过相对角度和距离判断，火控雷达威胁判断如式（1）所示：

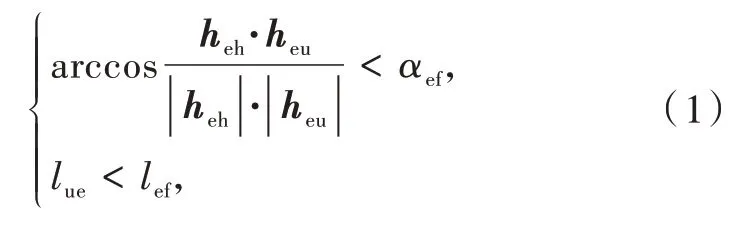
式中：heh为敌机航向向量；heu为敌机与我方无人机连线，方向指向我方无人机；αef为敌机火控雷达辐射角度的一半；lue为无人机到敌机的距离；lef为敌机火控雷达的作用距离。同理，电子干扰威胁判断如式（2）所示：

式中：αee1和αee2为电子干扰吊舱的辐射角度范围；lee为电子干扰的作用距离，且通常条件下电子干扰的作用距离会大于火控雷达的辐射距离以实现防卫的目的。

2 武器发射达成条件

在中距空战对抗中，航空器使用的武器主要指空空导弹，其必须达成2 个条件才能发射，一是敌机被机载火控雷达锁定，二是在空空导弹的最大发射距离之内。因此，无人机在机动过程中，除避开敌机武器威胁外，还需要积极达成武器发射条件。从图1 中可以看出，在我火控雷达作用距离小于敌机火控雷达和电子干扰作用距离的情况下，攻击敌机的最佳方法为实施尾后攻击。而事实上，无人机由于机体较小，载荷能力受限，其携带的火控雷达工作距离往往会小于有人机的火控雷达，以对头或侧方位的进入方式都不能构成有利态势，最佳的攻击方位便是实施尾后攻击。无人机武器发射应当满足：

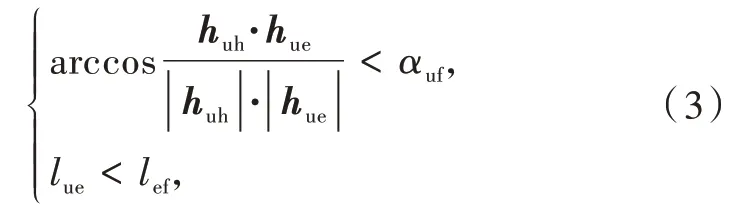
式中：huh为无人机的航向向量；hue为无人机到敌机的方向向量；αuf为无人机火控雷达辐射角度的一半；lef为无人机火控雷达的工作距离。

3 基于A-star 算法的侧向机动算法

3.1 基本A-star 算法

A-star 算法是一种较为经典的启发式搜索算法，该 算 法 于1968 年 由P.E.Hart 等 提 出［16］。A-star 算法将Dijkstra 算法和BFS 算法的搜索策略结合了起来。Dijkstra 算法以起始点为中心依次外推，以寻找距目标点最短的路径。BFS 算法是一种启发式的搜索策略，具有搜索快速的特点，它先对当前点与目标点之间的路径距离进行估算，并选择与目标点距离最近的待选节点作为下一节点。但BFS 存在明显的缺陷，不能保证找到最优解［17］。

A-star 算法将2 种算法的优势相结合，既加入了启发式信息函数以提高搜索速度，又考虑了当前节点的历史代价信息，具有路径寻优能力强、规划速度快的特点。相对于蚁群算法［18］和遗传算法［14］，Astar 算法的全局规划能力稍弱，但具有更快的规划速度，其每一步的决策主要是基于历史信息和局部信息，使其规划速度也显著提升，可以满足空战对抗中态势更迭迅速的决策需求。其不依赖全局信息的特性也使其可以应对更大的规划空间。算法的代价函数为

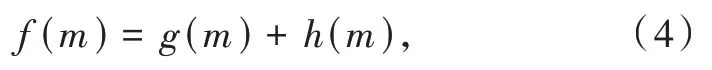
式中：g(m)为当前节点m的历史代价信息；h(m)为节点m未来的代价估计。根据路径点状态转移规则的不同，需要制定open 表和close 表。算法从起始点开始计算open 表中的节点相应的代价值并选择最优的节点作为下一节点进行状态转移。状态转移之后需要更新open 表和close 表，同时将待选节点的父节点记为当前节点，依次类推直至达到终点。当遇到待选节点为空的情况时，需要将当前节点放入close 表中，并将状态回退至父节点进行重新计算下一节点。到达终点后，根据各个节点记录的父节点信息进行回溯即可完成路径的规划，算法流程如图2 所示。

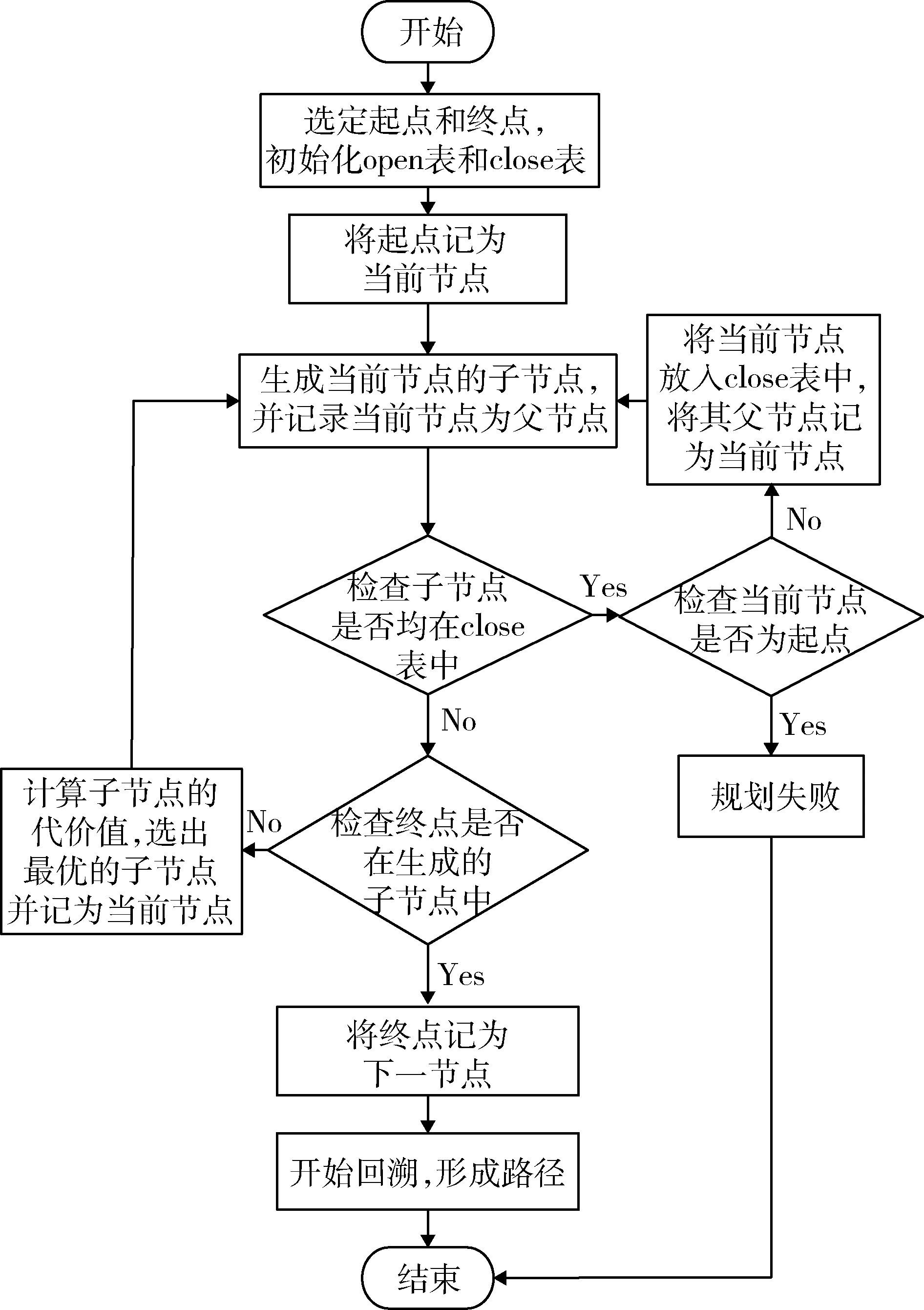
图2 A-star 算法流程图Fig.2 A-star algorithm flow chart

3.2 动态栅格规划环境构建

A-star 算法对路径的规划需要有离散化的规划空间，通常采取的措施是按照地理环境或空间构设一个静态栅格环境。静态栅格环境可以较好地满足目标侦察、低空突防、转场飞行等任务的规划，但对空战对抗任务而言，态势以敌我相对位置为判断依据，因此需要建立动态的栅格规划空间。本文采取以敌我相对位置来确定栅格规划环境的方法，根据变化的敌我态势调整栅格环境，如图3 所示。

图3 动态栅格环境图Fig.3 Dynamic grid environment map

栅格环境相对敌我飞机而言始终固定，但相对大地坐标而言在不停地旋转，其单位步长的尺寸也在拓展或收缩。栅格坐标的旋转变换公式为

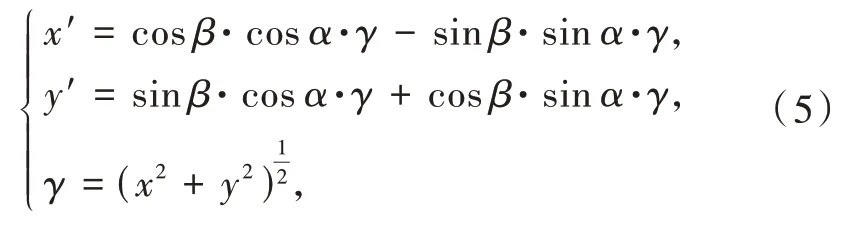
式中：(x，y)为栅格坐标系坐标；(x′，y′)为大地坐标系坐标；α为栅格坐标与大地坐标所成的角度；β为无人机在栅格坐标中的位置向量与x轴形成的夹角，规定逆时针旋转为正。采用动态栅格环境规划路径可以使规划空间保持不变，始终维持规划速度的品质。

3.3 侧向机动算法设计

在栅格环境内，无人机位置状态的转移会有一定的规则限制，从而满足航空器转弯率的最大限制。无人机以敌机当前位置为规划终点前进，单次状态转移过程中只考察临近符合转弯率限制的节点，计算其代价值。设置的状态转移规则如图4所示。

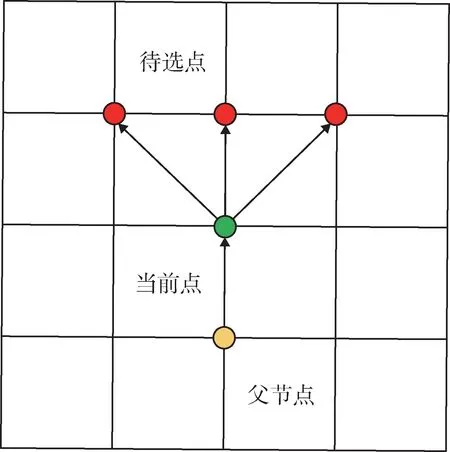
图4 无人机侧向机动状态转移规则Fig.4 UAV lateral maneuvering state transfer rules

无人机当前节点的上一节点为父节点，邻近节点中符合转弯率的节点为待选节点。对待选节点进行依次计算，得出最优的节点。由于缺乏适当的启发式因子，传统的A-star 算法并不能很好地进行“咬尾”机动，只能在向目标点突进的过程中进行威胁规避，这样会影响空战机动的效率，因此本文加入了一个启发式因子，作为“咬尾”路径的引导，如图5 所示。

图5 无人机路径引导点示意图Fig.5 Schematic diagram of UAV path guidance points

p1至p4分别为无人机在各个阶段的路径规划引导点。无人机在接近敌机的过程中随着距离的接近不断变化引导点，可以使无人机更好地从尾后实施攻击。状态转移中的代价函数为

式中：g（n）为代价函数中的历史信息，计算路径中在敌机火控雷达和电子干扰区内的路径长度；Cf为火控雷达的威胁系数；Ce为电子干扰威胁系数；l为节点n至敌机的距离，显然，距离越近，威胁对无人机的作用更强；h（n）为代价函数中的期望信息；Cd为距离代价系数；l*为节点n至引导点的距离，具体计算方法为

其中，l1~l4分别为无人机至点p1~p4的距离；θ为敌机航向向量heh与无人机至敌机的方向向量hue之间的夹角；θ1为敌机航向与威胁区域边界所成夹角（如图5 中所示）。

3.4 速度规划方法

无人机的速度规划需要根据任务实施阶段区别对待。无人机中距空战分为2 个阶段，分别为前出接敌阶段和战术机动阶段。在前出接敌过程中，无人机根据体系雷达信息靠近敌机邻近空域，在该阶段中主要以巡航速度飞行。在战术机动阶段，无人机需要通过快速的机动尽快抢占有利态势，在敌机威胁区域内时则需要加速摆脱威胁。

本文对速度的规划建立在规划的路径基础之上，通过对每一个路径节点规划加速度值的方式规划每一段路径内的速度变化方式。由于受发动机推力和机体气动性能限制，无人机的加速度同样有上下限，通过将加速度值进行离散化的方式计算每一个路径节点的最优速度控制方案。但以这样的方式仍无法满足空战对抗中快速的速度变化要求，因此论文在态势更新后的路径重规划中同时进行速度重规划，更新的的频率越高，路径和速度的变化越平滑，越能贴近实际的需求。速度规划目标函数如式（8）~（12）所示：

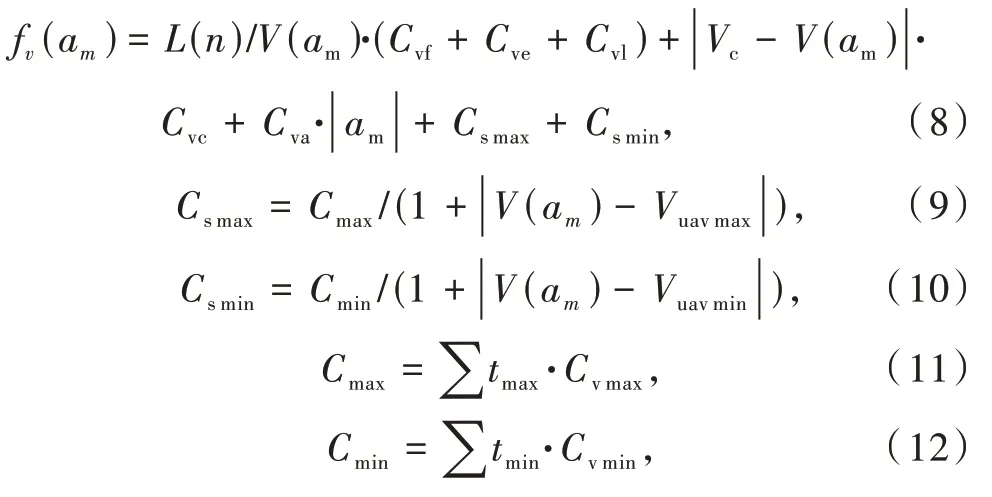
式中：am为离散化的加速度；L(n)为第n段路径的长度；V(am)为节点m规划的速度；Cvf，Cve，Cvl，Cvc，Cva，Cvmax，Cvmin均为常数；Vc为无人机的最佳巡航速度；Csmax和Csmin为无人机的最大、最小速度代价值，当无人机持续使用最大或最小速度时该代价值会累积增大；Vuavmax和Vuavmin为无人机的最大最小速度。

4 双机协同决策方法

4.1 基本战术策略

本文重点研究的是二对二中距空战。我方无人机前出接敌过程中面临的敌机编队有可能以2 种方式应对我机，一种是双机协作先合力击落我1 架无人机实现空中力量优势；另一种是双机各自分离，从不同方位对我构成攻击态势，力争尽早能够从一个方向上达成攻击条件。我方双机则需要根据敌机态势采取应对措施，对于第1 种情况则由1架无人机进行逃逸机动，避免被击落，另1 架则积极进攻，力争夺得空中力量优势；对于第2 种情况则采取编队分离，以“钳形”攻击战术与敌机抢占空中优势，尽早构成武器发射条件，战术决策流程如图6所示。

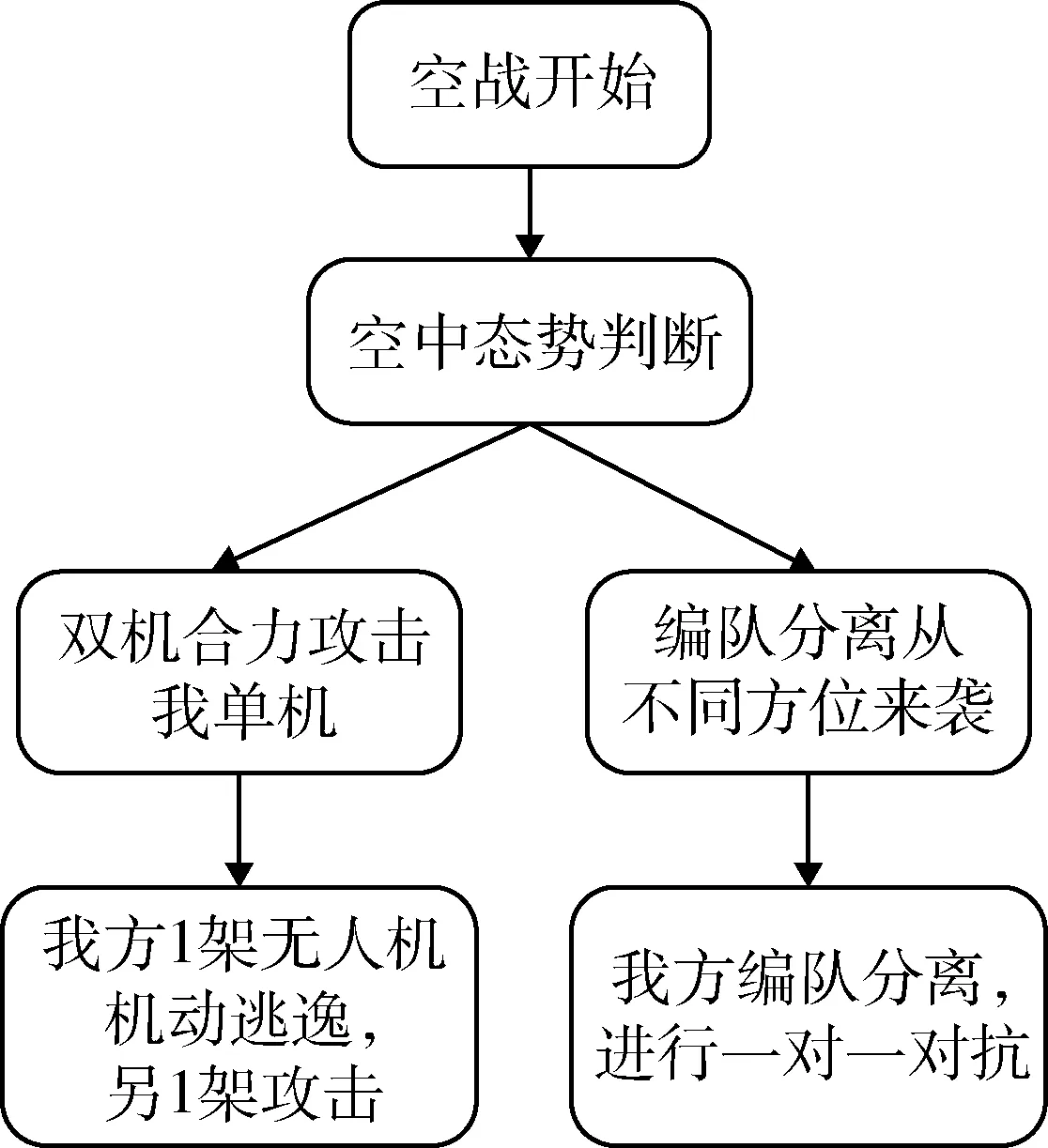
图6 无人机空战对抗战术决策流程Fig.6 UAV air combat tactical decision process

4.2 攻击目标分配函数

相对于一对一［12］或二对一［15］的空战对抗机动决策，在二对二的空战对抗中还需要进行目标分配以实现更好地协同。为尽早达成二对一的优势态势，需要无人机分别规划对敌机的攻击路径后进行信息交互，选择出最优的攻击方案，目标分配流程如图7 所示。

图7 无人机目标分配协同决策流程Fig.7 Collaborative decision-making process for drone target allocation

4.3 空战决策动态跟新策略

无人机的单次决策是基于当前态势的机动策略，随着敌我态势的转变，原有决策方案很快就会失效，因此需要根据变换的态势进行决策更新。在路径规划中，无人机首先对敌机态势进行一次更新，而后根据最新的态势规划机动方案。规划完毕后与编组无人机进行信息交互，计算最优的协同方案并完成协同决策。而后，在接下去的Δt时间内执行机动决策方案并展开新一轮的规划。由于算法设计中，对路径和速度的规划中对规划空间都进行了离散化处理，并不符合实际飞行的决策需求，因此需要加快迭代更新频率，提升决策方案的有效性。空战机动决策的总体流程如图8 所示。

图8 无人机双机对抗决策更新流程Fig.8 UAV dual-aircraft confrontation decision update process

5 仿真与分析

论文基于Matlab 构建无人机空战对抗仿真运行平台，首先进行单机对抗的路径规划试验，运行参数如表1 所示。

表1 无人机空战仿真参数设置Table 1 UAV air combat simulation parameter setting

无人机的空战路径仿真如图9 所示；图9（a）中速度规划曲线如图10 所示，无人机决策时间变化曲线如图11所示；无人机加速度变化曲线如图12所示。

图10 无人机速度变化曲线Fig.10 UAV speed curve

图11 无人机机动决策耗时曲线Fig.11 UAV maneuvering decision time-consuming curve

图12 无人机加速度变化曲线Fig.12 UAV acceleration change curve

从单机验证结果来看，无人机可以进行较好地机动并进行“咬尾”攻击。无人机的速度规划可分为3 个阶段进行：第一阶段为前出接敌阶段，在该阶段内无人机与敌机距离较远，既无法锁定敌机，也不会被敌机锁定，因此没有做大速度机动的必要，只需要以巡航速度接近敌机即可；第二阶段，无人机可能进入敌机的火控雷达照射范围内，且需要尽快锁定敌机，应进行大速度的机动，在避开敌机的同时形成咬尾态势；第三阶段为咬尾锁定阶段，当无人机形成优势态势之后，应当与敌机保持相对稳定的空中态势，以便于导弹能够进一步锁定敌机，因此速度又会再次回调。结合图9 b）的态势图可知，无人机的速度规划具备根据空中态势进行自适应调整的能力，算法设计有效。在决策时间方面，论文无人机决策的平均时间为0.015 7 s，人最快的视觉反应时间为0.15~0.20 s，随着态势的复杂度上升或生理状态的下降，人的反映时间会进一步加长。而航空器控制回路的反应时间可假设有人机与无人机相同。由此可见，相较于有人机的空战决策速度，无人机的决策效率显著提升，能够满足现有的空战对抗需求，算法同样有效。

图9 无人机单机空战航迹Fig.9 Single drone air combat track

再对双机空战对抗机动效果进行仿真验证，如图13 所示。

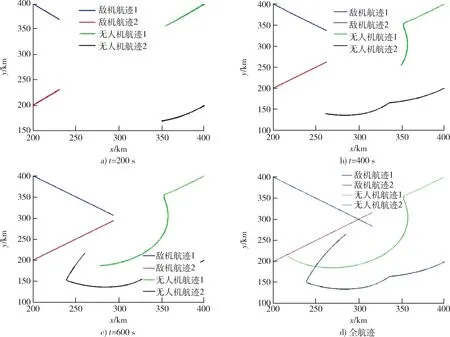
图13 无人机双机空战对抗航迹Fig.13 UAV dual-aircraft combat confrontation track

从双机对抗的仿真结果中可以看出，对于来自于不同方向的敌机，无人机能够进行较好地侧向机动，其中无人机航迹2 率先对敌机2 形成尾后攻击态势，若命中目标，则可形成二对一空战优势，锁定胜局。无人机航迹1 则继续追击敌机航迹1。

6 结束语

本文基于A-star 算法设计了无人机中距空战对抗中侧向机动“咬尾”攻击的决策方法，在路径搜索过程中，通过加入引导式的启发式因子，可使无人机在威胁规避的同时机动至敌机尾后实施攻击。从航迹决策时间和速度控制效果来看均达到了预期。在双机对抗中，通过内部决策的协同，按照尽快实现空中力量优势的原则分配对抗目标，能够完成双机协同下的侧向机动攻击。下一步将根据更多的空中态势和更复杂的情景，展开对应的机动方式的研究，丰富无人机的空战对抗决策库。