基于粗糙集和遗传算法的作战试验指标集优化方法*

陈小卫，杨超*，季自力

（1.航天工程大学，北京 102206；2.战略支援部队某部，北京 100084）

0 引言

构建科学合理的考核指标体系是开展武器装备作战试验的基础，直接决定试验内容和评估结论［1］。当前，关于作战试验指标构建方法主要有使命任务分解方法［2］、关键作战问题树状分解方法［3］、能力需求分析方法等［4-5］。现有指标体系构建方法能够形成较好反映装备特征，且较为全面的指标体系框架。但随着装备体系的日益庞大和作战过程的复杂化，指标数量也愈加庞大，若对指标体系框架内的所有指标全部进行考核，则会使得试验的复杂性和成本增加，甚至导致试验无法完成。而在实际作战试验过程中，某些指标对试验评估结论影响是不重要的，冗余的。为节约试验成本，优化试验内容和周期，有必要对指标体系进行优化，得到最简洁明了且能够反映实现作战试验考核目标的指标体系。

作战试验属于新体制下的试验模式，目前有关其指标体系优化的研究尚不多见，但是在其他领域，有关评估指标的筛选优化方法的研究很多［6-10］。从现有研究来看，评估指标筛选优化方法主要有3类：一是统计分析方法，如主成分分析法、因子分析法、相关系数法、条件广义最小方差法等，该类方法主要依赖定量的统计信息，缺点是忽视了人的主观认识所应发挥的作用；一类是基于专家主观意见的优化方法，如Vague 集、德尔菲方法等，该类方法优点是能较好的利用专家经验知识和主观判断，同时还能处理模糊性、不确定性指标信息，缺点是忽视了指标的客观信息；还有一类是基于知识挖掘型的筛选方法等，如粗糙集方法，该类方法能够对定性和定量信息进行分析挖掘，提炼出知识，实现智能化评价。粗糙集方法能够较好处理各类不确定信息，且较为简洁直观，被广泛引用到装备通用质量特性评价、社会可持续发展价、水源地安全供水风险评价等领域［6，10］指标优化中去，取得了良好的成效。考虑到作战试验环境复杂，定性定量指标信息并存，而粗糙集方法能够实现这类信息的分析处理。为此，本文将粗糙集理论应用到作战试验中去，构建针对性优化模型，为作战试验指标和内容优化提出新的技术途径。

1 基于粗糙集和遗传算法的作战试验指标优化方法

作战试验是在近实战环境和对抗条件下，运用多种试验方法手段，对武器装备完成作战使命任务的作战效能与适用性等进行的综合性的检验活动，确保能够为用户提供满足要求的武器装备［11］。其目的是为武器装备列装定型提供决策依据。

试验指标是对被试装备的本质特征、结构及其构成要素的客观描述和准确表达，是开展试验鉴定活动的基础。通常在编制作战试验大纲时，需要建立评估指标体系。作战试验指标构建应遵循目的性、完备性、独立性、简明性等原则。在作战试验指标构建的过程中，会综合考虑大量定性、定量指标，为避免指标之间重复和交叉，确保独立性和简明性，指标的筛选和优化是指标体系构建的重要环节。

粗糙集理论于1982 年被波兰学者Z.Pawlak 提出。它能有效地分析各种不确定的信息，通过属性约简，去除不必要的属性，从而实现知识发现，在人工智能、数据挖掘、决策分析等各个领域有着广泛的应用［12-13］。由于作战试验涉及环境因素复杂，定性定量指标共存，试验指标存在大量不确定信息，为此，本文采用粗糙集方法，对作战试验指标体系进行优化。

1.1 构建作战试验指标体系框架

综合运用采用能力需求分析、关键作战问题树状分解等方法，形成初步的作战试验指标体系框架。初步构建的指标体系是一个大而全的指标体系框架，有部分指标对试验鉴定结论影响不大，是不重要的，应予以删减优化。下面利用粗糙集属性约简的思想对指标体系进行优化。

1.2 构建决策信息表

运用粗糙集方法对作战试验指标进行筛选和优化，首先应收集指标信息，构建作战试验指标决策信息表。

定义1设U={x1，x2，…，xn}为对象的非空有限集合，也称论域，A={a1，a2，…，am}为属性的非空有限集合，为 属 性 值 域，f：U×A→V为 一信息函数，表示对每一个a∈A，x∈U，f(x，a) ∈Va，则称S=(U，A，V，f)为信息系统。当信息系统中属性A=C∪D，且C∩D=∅，其 中C={c1，c2，…，c3}为条件属性的非空有限集合，D={d}为决策属性集时，信息系统也称为决策系统。

以作战试验指标体系框架中的各指标作为条件属性，评估结果作为决策属性，可建作战试验指标决策信息表，形式如表1 所示。其中C1，C2，…，Cn为条件属性，分别对应于作战试验各指标值，x1，x2，…，xn对应于各评估样本，d为决策属性，对应于评估结果。关于指标数据，主要来源于历史数据、同类装备、建模仿真、专家信息等。

表1 作战试验指标决策信息表Table 1 Decision information of operational test index system

1.3 基于遗传算法的属性约简方法

在构建作战试验指标决策信息表后，可对其进行属性约简，去除冗余属性（指标），从而得到简化的指标体系。下面给出属性约简相关概念。

定义2设有决策信息系统S=(U，C∪D，V，f)，其中C为条件属性集，D为决策属性集，则决策属性集D在条件属性集C下的正域为

下面给出属性约简的概念。

定义3设决策系统S=(U，C∪D，V，f)，C为条件属性集，P为集合C的一个非空子集。若它满足：

（1）∀a∈P，a都是不可省略的；

（2）POSP(D) =POSC(D)。

则称P是C的一个约简，C中所有的约简集合记作RED(C)。对于约简结果可能有多个，所有C的属性约简的交集称为C的核，记为Core（C）。

通常，可采用基于属性依赖度的方法进行属性约简。

定义4决策属性D对条件属性C的依赖度定义为

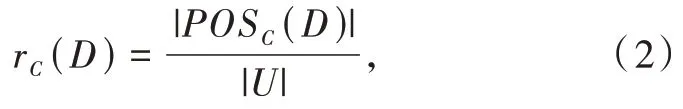
式中：“|•|”表示集合的基数。式（2）称属性集D在rC(D)程度上依赖于属性集C。通常0 ≤rC(D) ≤1，当rC(D) = 1 时，表示决策属性D中所有的属性值都由条件属性集C中的属性值决定，则称决策属性D完全依赖于C；rC(D) ＜1 表示决策属性D中的部分属性值由C中的属性值决定，则称D局部（在rC(D)程度上）依赖于C。

粗糙集的属性约简，是一个NP-Hard 问题，其主要原因是属性之间的组合爆炸问题。针对这类问题，可采用遗传算法进行求解［14］。遗传算法是是一种通过模拟自然进化过程搜索最优解的方法。下面介绍基于遗传算法的属性约简的基本过程：

（1）编码

采用遗传算法首先要解决编码的问题。本文采用二进制编码方法进行编码。设有n个条件属性C=｛C1，C2，…，Cn｝，则可将条件属性所有子集用长度为n的二进制字符串来表示。该字符串每位的取值范围为｛0，1｝，若取值为1，则表示选择该属性；若取值为0，则表示去除该属性。例如设条件属性个数n=5，则二进制字符串11001 对应的属性子集为｛C1，C2，C5｝。按照这种编码方式，可将每个属性与遗传算法的染色体映射起来，每个二进制字符串对应于一个染色体，每个二进制位对应于一个取值范围为｛0，1｝基因。

（2）构建适应度函数

遗传算法以适应度函数为依据进行搜索。参考文献［14］给出的适应度函数，设对于任意染色体s，其适应度如下：

式中：ls表示染色体s中基因值取1 的数量；rs(d)表示决策属性d对染色体s对应的条件属性子集的依赖度。

由定义3 可知，属性约简集实质就是在属性依赖度不变的情况下，找到条件属性个数最少的子集。可以发现，该适应度函数综合考虑属性子集元素个数和属性依赖度两方面的因素。为此，可以控制染色体向最小属性约简集进化。

（3）选择

运用轮盘赌选择作为选择操作算子。其中，个体被选择的概率为

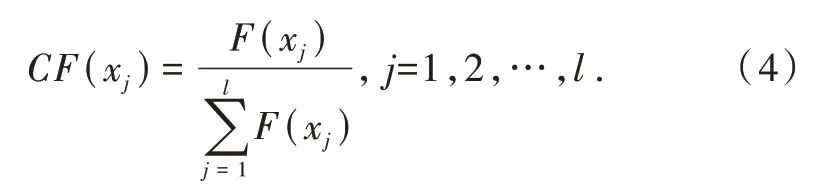
（4）交叉

选用单点交叉方法进行交叉操作。针对2 个相互配对的染色体，以设定的概率Pc在交叉点互换部分染色体，从而产生了2 个新的个体。

（5）变异

采用均匀变异算子进行变异运算。设定一个变异概率Pm，而后以概率Pm随机反转某位等位基因的二进制字符值，从而实现变异。

（6）最优保存策略

在得到新一代个体之后，如果其中适应值最小的个体的适应值小于上一代适应值最大（最优）的个体，则用适应值最大的个体个体替代新一代适应值最小的的个体，通过该方法能确保算法收敛。

（7）循环终止条件

当迭代步数达到设定的最大代数或者属性集依赖度rreduct(D) =rC(D)时停止运算。

算法描述如下：

输入：决策信息系统S=(U，C∪D，V，f)

输出：决策信息系统S的所有约简。

算法步骤：

Step 1：由式（2）计算条件属性相对于决策属性的依赖度rC(d)；

Step 2：计算条件属性的核core(C)。令core(C) =∅，逐个去掉一个属性ci∈C，若rC-{ci}(D) ≠rC(D)，则core(C) =core(C) ∪{ci}；若rcore(C)(D) =rC(D)，则 终止运算，core(C) 即为最小相对约简，否则转入Step 3；

Step 3：设条件属性集的个数为n，随机生成长度为n 的二进制串所代表的个体，组成初始种群，并计算初始群体中所有个体的适应度；

Step 4：采用轮盘赌策略进行选择操作，采用式（4）可计算个体被选择的概率；

Step 5：分别以交叉概率P以及变异概率Pm，进行交叉和变异操作，从而产生新一代群体；

Step 6：计算新群体中所有个体的适应度，其计算公式如式（3）所示；

Step 7：按照前面的最优保存策略，把新一代适应值最大的个体替代到下一代群体中，同时保存最优个体；

Step 8：判断是否连续t代的适应值最大的个体，其适应值不再增加。若不增加则终止计算，并输出最优个体，反之则转Step 4。

1.4 获取简化的指标集

通过属性约简，可得到作战试验指标决策信息表的属性约简集，该约简集则对应于简化的试验评估指标体系。

通过以上计算过程可以发现，基于粗糙集的指标体系简化方法就是不断去除冗余的或不必要的指标，直到剩余必要指标为止的过程。

基于粗糙集和遗传算法的的指标体系简化流程如图1 所示。

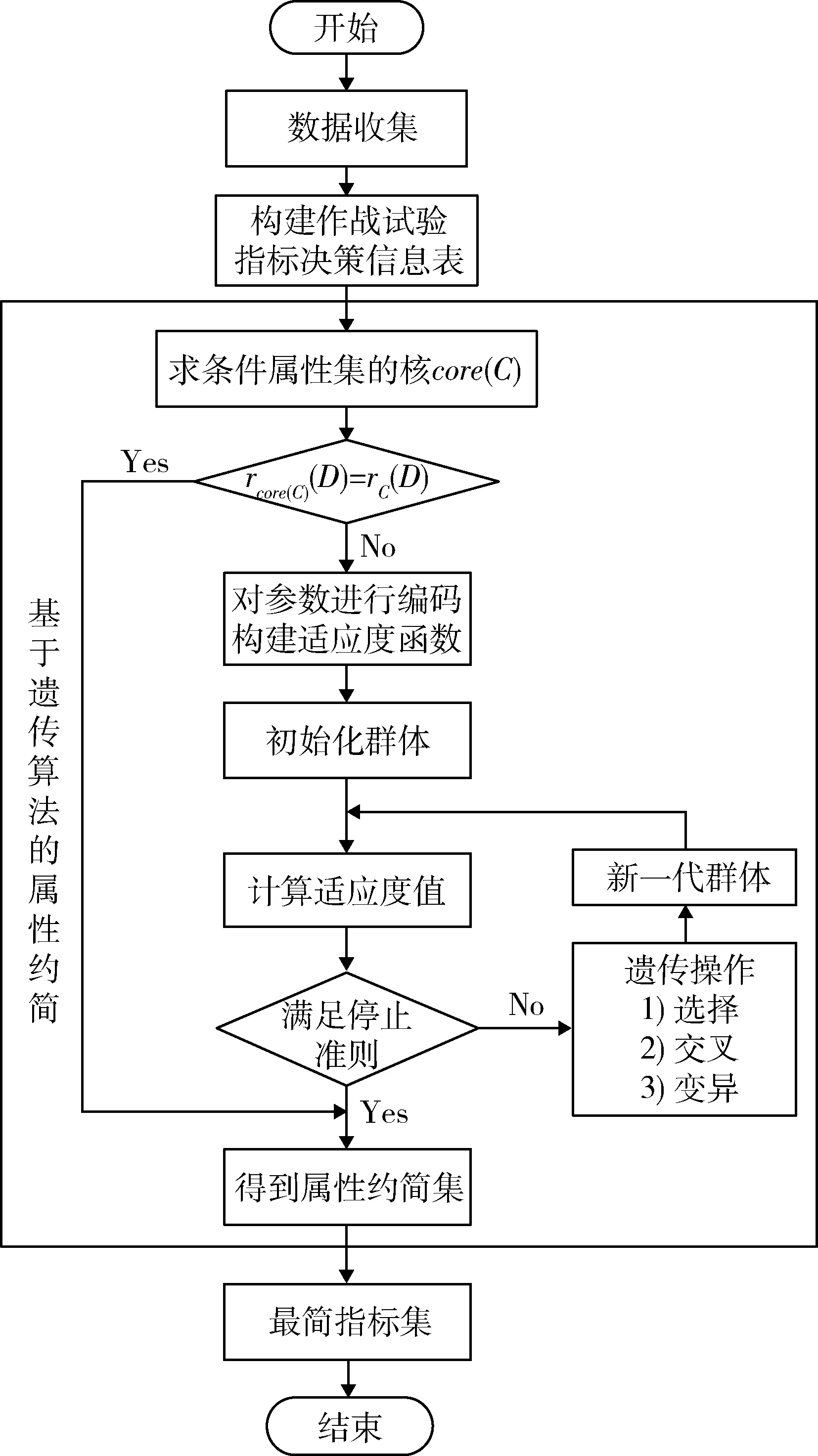
图1 作战试验指标优化方法流程图Fig.1 Flow chart of operational test index set optimization

2 算例分析

以某高炮武器作战试验中火力运用效能试验科目为例，运用前面提出的方法进行指标优化。从装备使命任务出发，在分析其能力需求，构建火力运用效能试验指标体系基本框架，如表2 所示。

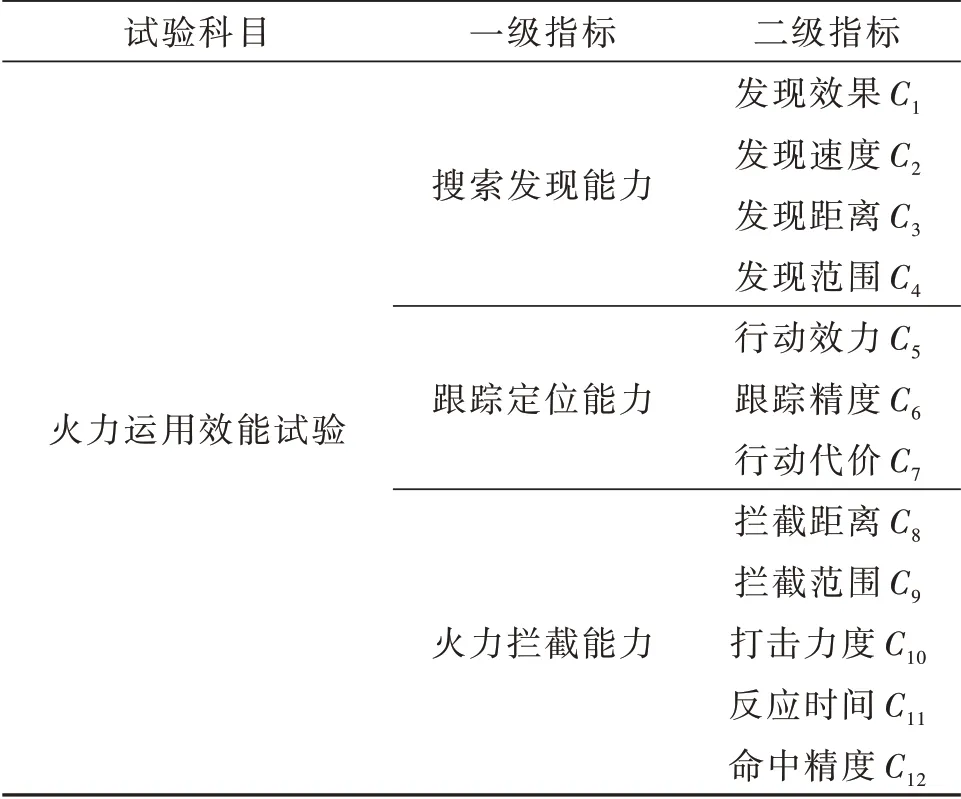
表2 某高炮武器火力运用效能试验指标体系框架Table2 The index system framework of anti-aircraft gun weapon fire operational effectiveness test

各指标量化标准如表3 所示。

表3 各指标量化标准表Table3 The indexes quantitative standard

通过收集同类型装备历史数据，并邀请专家打分，获取指标信息。以C1，C2，…，C12为条件属性，作战效果d为决策属性，选取20 组评估样本，可构建表4 某高炮武器系统作战试验指标决策信息表。

采用基于遗传算法的属性约简方法，对表4 某高炮武器系统作战试验指标决策信息表进行属性约简。选取交叉概率Pc=0.7 和变异概率Pm=0.01，可得到一个最优解为110101010111，即可得到属性约简集为｛C1，C2，C4，C6，C8，C10，C11，C12｝。为此，可得到优化的三级指标为8 个：发现效果、发现速度、发现范围、跟踪精度、拦截距离、打击力度、反应时间、命中精度。减少了发现距离、行动效力、行动代价、拦截范围4 个指标。通过分析可以发现，对于该高炮武器系统，其主要作战使命任务为拦截空中来袭目标。对同一空中来袭目标，其发现范围涵盖了发现距离指标，而拦截范围核心体现在高炮武器与目标直接的斜距上，因此，指标内涵具有交叉。同时，跟踪定位过程中，行动效力和行动代价对跟踪定位能力影响较小。为此，指标优化的结果较为符合实际情况。

表4 某高炮武器系统作战试验指标决策信息表Table4 Decision information of anti-aircraft gun weapon system operational test index system

计算过程可以发现，通过属性约简，得到了简化的指标体系。而基于简化的指标体系，试验需要考核的指标从12 个减少了8 个，简化了试验内容，优化了试验科目，节约了试验成本。

3 结束语

随着武器装备的发展，作战试验鉴定的对象由单装、系统到体系，其试验考核指标和内容愈加复杂。粗糙集方法能够有效处理不确定信息，并通过属性约简，去除冗余的、不重要的指标，实现信息“降维”，在试验鉴定的数据分析处理领域有着广阔的应用前景。本文提出了一种基于粗糙集和遗传算法的作战试验指标优化方法，在构建作战试验指标决策信息表的基础上，运用遗传算法求取属性约简集，实现初始指标体系框架的优化，从而得到相对简化的指标体系，对提升试验效率，节约试验成本具有重要意义。由于作战试验环境的复杂性和决策者的主观性，指标数据采集过程中，往往会出现不一致、不完备等情形，如何实现这些不确定信息下的指标优化，这将是下一步的研究方向。