末段反导装备资源配置优化研究*

余伟军，史朝辉，周峰，李京泰

（1.空军工程大学 防空反导学院，陕西 西安 710051；2.中国人民解放军32705 部队，陕西 西安 710086）

0 引言

面对快速发展的弹道导弹技术，各军事强国面临日益严峻的反导压力。在更新发展反导技术和反导装备的同时，如何利用有限的反导资源对保卫对象实施有效保护，不同时期的专家学者也提出了不同的解决方案。文献［1］利用步长推进算法给出了反导装备配置区域优化的思路；文献［2］提出了一种基于评估结果对配置方案进行优化的方法；文献［3］引入改进基本微分进化算法（MPDE）解算了末段高低两层协同反导火力分配模型；文献［4］提出了一种基于结构方程模型（SEM）的部署优化设计方法。战前反导装备资源的优化配置，既是反导作战筹划的必要过程，更是影响反导作战效能的直接因素，因此开展末段反导装备资源优化配置研究无疑具有重要的实战价值和现实意义。

1 末段反导装备资源配置问题概述

弹道导弹的飞行末段，也称再入段，这一段飞行时间短、弹头速度快，是反导拦截的最后阶段［5］。针对此阶段弹道导弹的拦截又区分为末段高层拦截和末段低层拦截，是重要的弹道导弹防御力量。由于弹道导弹飞行末段弹头速度快，RCS 小，给予反导火力单元的作战时间十分有限。战前进行末段反导装备资源配置，决定了作战过程中火力分配、拦截成本和拦截效率，因此如何利用有限的反导装备资源在作战时间内高效率、低成本完成拦截任务，战前进行装备资源的优化配置就显得十分重要。在配置过程中，通常考虑以下三大方面的因素。

1.1 保卫目标

反导作战的保卫目标包括中大型城市（人口聚集地）、军事设施、大型基础设施等。根据目标价值、保卫迫切程度和保卫目标的工程特性对保卫目标进行综合评估，得到被保卫目标的优先级排序［6-7］。

通常将保卫目标分为0~4 级共5 个防御等级［8］：

0 级：无防御级，无需提供任何防御；

1 级：低防御级，提供最小防御；

2 级：中级防御，提供中等强度防御，是最常用的一种防御级别；

3 级：高级防御，提供高强度防御；

4 级：最高级防御，对易受攻击的最高优先权目标提供防御。

根据相应的防御等级，结合武器装备的性能参数进行合理配置，进而对来袭目标进行高效拦截。

1.2 来袭弹道导弹

弹道导弹突防有以下3 个特点：①弹道导弹都是预先设定突防措施，发射后依照预设程序突防，不能人工干预和及时变更；②突防手段不是唯一的，通常根据敌方反导装备作战效能和兵力配置规模，有针对性地制定多种突防措施，综合各类有效信息，达到突防目的；③无论怎样设计和采取何种突防手段，弹道导弹最终目的都是有效攻击敌方地面保卫目标，这是组织开展反导作战研究和配置规划的基点。

在作战筹划时，根据相关情报与先验知识，本文主要考虑来袭弹道导弹接近目标剩余时间、打击目标的抗毁伤能力、来袭弹道的突防方式和来袭弹道的数量四个因素［9］，这些因素可以构成末段反导装备系统部署优化的输入条件。

1.3 反导武器装备

末段反导指在来袭弹道导弹飞行的再入段对弹道目标实施的拦截作战活动，对于确定的弹道导弹发射点、来袭方向和目标类型，末段反导保卫区可以描述为末段反导作战单元杀伤区沿来袭弹道导弹弹道方向在地面的投影［10］，只要保卫目标在该区域内，就可以受到反导作战单元的拦截保护，从而免受弹道导弹攻击。末段反导保卫区如图1所示。

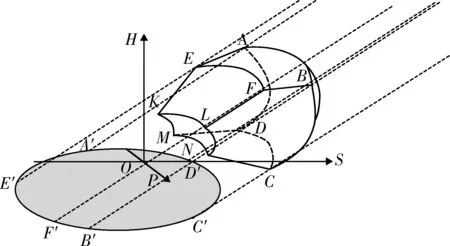
图1 末段反导保卫区示意图Fig.1 Schematic diagram of the terminal anti-missile defense area

图中A′D′C′B′F′E′（阴影区域）即为末段反导作战单元对来袭弹道导弹目标的保卫区。末段高层反导武器具有作战空域范围大的特点，末段低层反导武器覆盖了临近空间的较低空域，可对末段高层反导武器拦截失败的来袭目标进行再拦截。

2 末段反导装备资源配置模型

2.1 配置原则与初始条件

为建立优化配置模型，需要确定配置准则和初始条件，通常我们认为，反导武器装备资源配置需要符合以下原则［11］：

（1）首先考虑相对重要度高的任务，确保资源首先分配在最为重要的任务上；

（2）相应的作战资源能够兼顾每项任务；

（3）资源配置的最终目的是实现反导装备系统作战效能的最大化。

在遵循以上原则的基础上，还需要设定一些初始条件：

（1）反导装备的反弹道导弹杀伤区以及拦截概率已经确定；

（2）反导装备处于正常工作状态，且各火力单元导弹储备量是已知的；

（3）掌握来袭弹道导弹性质，落点判明且各参数确定；

（4）已经确定保卫目标的防御等级，依据防御等级和反导装备的性能指标确定不同防御等级下的最低拦截概率；

（5）一套反导火力单元只能覆盖一个保卫目标，一个保卫目标可以由多套反导火力单元覆盖。

2.2 配置模型建立

建立一个行之有效的配置模型十分重要，若配置模型考虑要素少，则模型过于简单，不贴合实战，参考价值不大；若配置模型考虑要素太多，则模型过于复杂，解算时间久且不易求得理想解。因此，在配置模型建立过程中应当筛选影响因素，使配置模型科学合理，易于寻找理想配置方案。

2.2.1 保卫目标相对重要度的确定

提出相对重要度这一概念可以对保卫目标的重要性进行定量化分析。定义一个保卫目标相对于所有保卫目标的保卫重要程度为保卫目标的相对重要度，越重要的保卫目标相对重要度越高，所有保卫目标的相对重要度值的和为1。德尔菲法能够对多个数量指标的相对重要度进行预测，如影响某事件的各要素的相对重要度［12］。在确定防御等级的基础上，我们利用德尔菲法对保卫目标进行定量化处理，得到各保卫目标的相对重要度。相关公式表示如下：

式中：sm表示编号为m的保卫目标的相对重要度。

2.2.2 保卫目标生存概率分析

保卫目标防御等级根据要求的生存概率确定，每一防御等级下有保卫目标的最低要求拦截概率P。根据防御等级选择末段高低两层反导装备的部署数量（套），则保卫目标生存概率Pm计算公式为

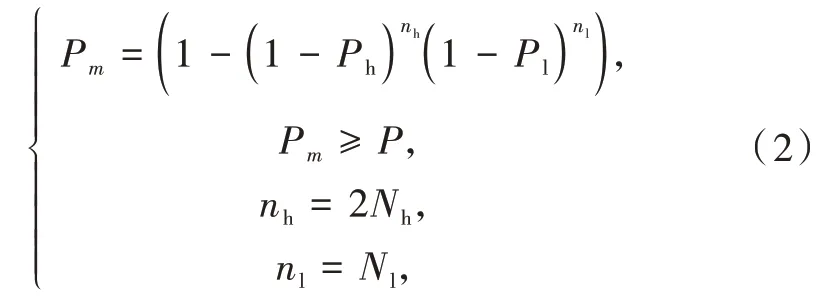
式中：Pm为编号为m的保卫目标的生存概率；Ph，Pl为末段高低两层反导装备单次的拦截概率；nh，nl为末段高低两层反导武器装备发射拦截次数；Nh，Nl为末段高低两层反导武器装备套数。一般末段高层火力单元对来袭目标优先进行拦截，一套火力单元至多对同一来袭目标可以拦截2 次，而一套末段低层火力单元对同一来袭目标至多只能拦截1 次，当单火力射击不能满足防御要求时，为提高拦截效率，可采取多火力单元集火射击方式。

2.2.3 保卫效益

综合考虑保卫目标防御等级和生存概率，提出保卫效益概念，这里把保卫效益Em定义为保卫目标相对重要度Sm与保卫目标生存概率Pm的乘积，即：

在此模型基础上，保卫效益E取最大值时，便是最优的末段反导装备资源配置方案，即：

3 算例分析

下面以具体算例验证末段反导装备资源配置模型的合理性和有效性。假设有5 枚来袭弹道导弹分别对5 个保卫目标进行袭击，5 个保卫目标的防御等级分别为0 级、1 级、2 级、3 级、4 级，配置前已经运用德尔菲法对5 个保卫目标的相对重要度进行了评价，评价结果为（0，0.05，0.10，0.25，0.60），设定对应的保卫目标最低要求拦截概率P分别为0，0.85，0.90，0.92，0.95，通过先验知识已经判明来袭弹道导弹对于保卫目标的攻击数量分配如表1 所示。

表1 来袭弹道导弹攻击目标分配情况Table 1 Target distribution of incoming ballistic missiles

现分别有末段高低两层反导装备各5 套，设定末段高低两层反导装备单次综合拦截概率分别为0.75 和0.60［13］，根 据 上 述 模 型 确 定 最 优 化 配 置方案。

4 基于天牛须搜索算法的反导装备配置优化

末段反导装备资源配置属于典型的多目标非线性规划问题，模型求解过程复杂，传统的算法（诸如暴力搜索算法）较为繁琐，不适应反导作战时效性高的要求，因此本文引入改进的天牛须搜索算法（BAS）对模型进行求解。

受到天牛寻偶及觅食行为的启发，Jiang 等于2017 年提出天牛须算法（Beetle Antennae search al⁃gorithm，BAS）［14］，作为一种单体搜索算法，区别于其他仿生类算法，具有计算量小、参数少、原理简单等优点，相较于大多数群体智能算法，其空间和时间复杂程度较低，效率也更高，在不知道梯度信息等的前提下可以实现优化目的，具有较强搜索能力，适用末段反导装备资源配置这类多目标非线性规划问题的求解。

4.1 算法简介

天牛须搜索算法是受到天牛觅食原理启发而开发的算法。在寻找食物过程中，食物会产生特殊气味，吸引天牛向目标前进，而天牛并不知道食物的具体位置。通过两只触角，天牛可以对空气中的目标气味进行感知，且根据目标距离两只触角的距离不同，两只触角所感知的气味浓度也有所不同。当食物位于天牛一侧时，近侧触角感知的气味浓度强于远端触角感知的气味浓度，天牛通过两只触角所感知的浓度差，向着浓度强的一侧随机前进。通过这一简单原理，最终找到目标位置［15］。目标函数就相当于食物的气味，并且在三维空间每个点值都不同，通过两个须采集附近的气味值，天牛可以找到全局气味值最大的点。依照天牛的生物学特点，我们就可以高效的进行函数寻优。

4.2 算法模型

为求解目标函数f在D维空间中的最小值，设天牛的质心坐标为X0，左须坐标为Xl，右须坐标为Xr，左右两须之间的距离为d0，左右两须同质心之间的距离为l。由算法简介中的寻优策略可知，由于天牛的头部朝向是随机的，所以由浓度强一侧天牛须指向浓度弱一侧天牛须的向量方向也是随机的，在此用随机向量d来表示这个向量。相应的表示及处理如下：

在进行感知气味浓度计算之前，需要进行相应准备工作，天牛在D维空间中的位置X=(X1，X2，X3，…，Xn)，天牛2 只触角的位置表示为

其中：d为随机单位向量，需对其进行归一化处理：

对比2 只触角感知的气味浓度差，判断天牛下一步的位置：

式中：t为当前迭代次数；f(.)为适应度函数；δt为第t次迭代时的步长；sign(.)为符号函数；eta为步长因子，各个变量的具体定义为

简化模型如图2 所示。

图2 天牛须搜索算法简化模型Fig.2 Simplified model of the Beetle antennae search algorithm

4.3 优化配置目标函数

根据前文所述的配置模型，要得到保卫效益的最大值，就要确定保卫效益最小损失值即目标函数为

式中：im为m等级保卫目标的相对重要度；xm为m等级保卫目标生存概率，其中：

式中：Ph，Pl为末段高低两层反导装备的单次拦截概率；nh，nl为末段高低两层反导武器装备的拦截次数，其他相关约束条件在本文第3 部分算例分析中已经给出。

运用天牛须搜索算法（BAS）对目标函数最优解进行寻优搜索，达到优化末段高层反导武器装备套数Nh和末段低层反导武器装备套数Nl两个参数的目的。流程示意图如图3 所示。

图3 天牛须搜索算法流程图Fig.3 Flowchart of the Beetle Antennae Search algorithm

4.4 实验分析

本文采用Matlab 编程语言（版本R2019b），在Windows10 试验平台上进行仿真试验。

在优化BAS 内部参数的过程中，通过单因素实验、正交分析确定初始步长δ0取1，距离步长因子eta=0.95，天牛质心与触须的距离l取1（左右两须之间的距离为d0取2）。实验条件：函数维度10 维，最大迭代次数1 000 次［16，17］，实验结果如图4 所示。

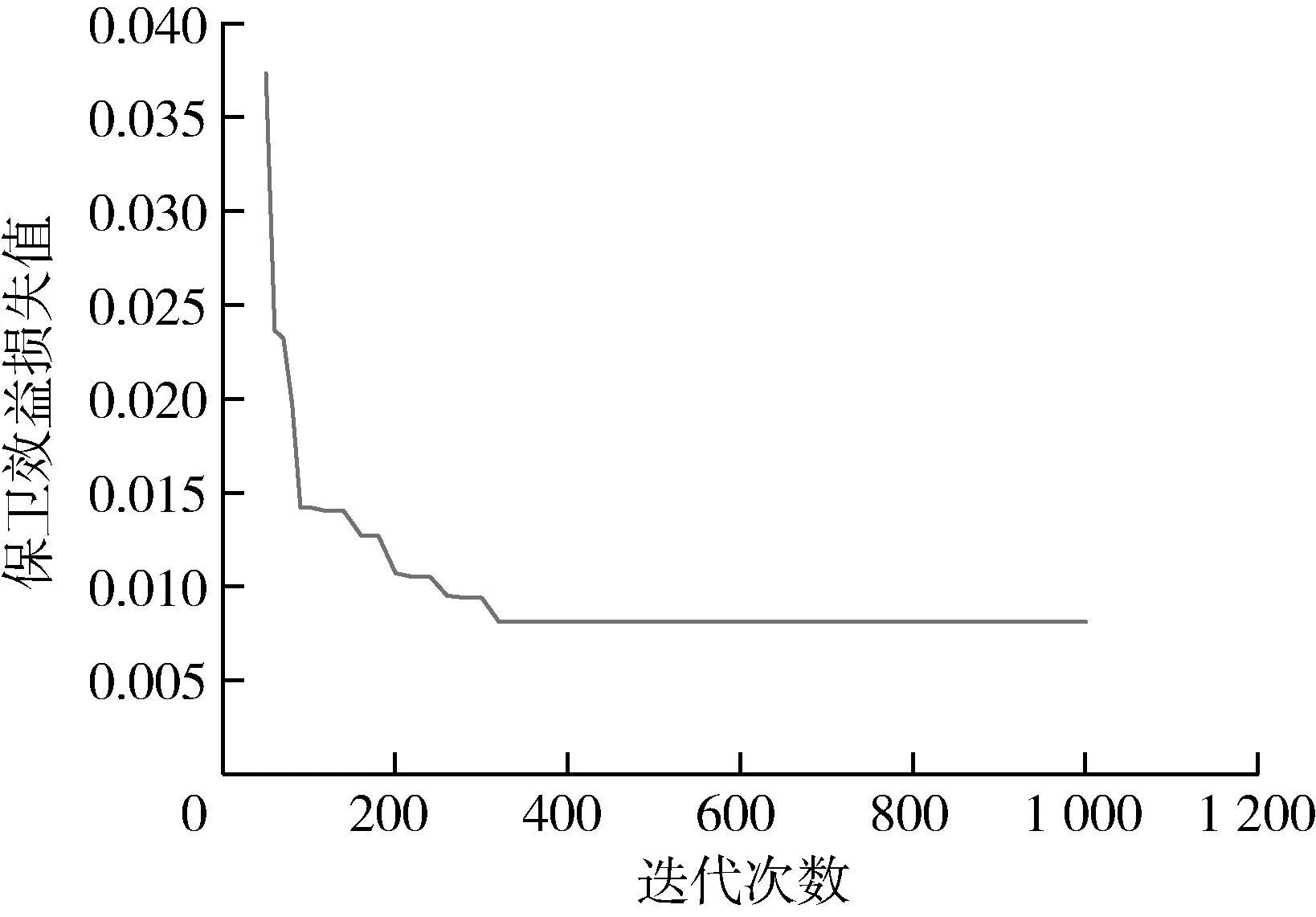
图4 迭代次数与保卫效益损失值Fig.4 Number of iterations and the loss value of defense benefits

通过仿真结果分析，应在0 防御等级保卫目标配置末段高低反导装备各0 套；1 防御等级保卫目标配置末段高低反导装备各1 套；2 防御等级保卫目标配置末段高低反导装备各1 套；3 防御等级保卫目标分别配置末段高低反导装备1 套和2 套；4 防御等级保卫目标分别配置末段高低反导装备2 套和1 套，使得保卫效益损失值最小，为0.008 1，即保卫效益最大，此时最大保卫效益值为0.991 9。

从实验结果来看，在有限的装备条件下，通过优化配置，达到了“重要目标重点防护，保卫目标全部覆盖”的防御要求，也反推验证了此优化配置模型的科学性和合理性，在实际配置部署过程中具有一定的参考价值。

5 结束语

本文给出了末段反导武器装备在配置规划时需要考虑的因素，在此基础上建立了配置模型，运用天牛须搜索算法（BAS）对具体算例模型进行了实验分析，对反导装备配置部署提供了一定参考。在反导装备资源配置实际过程中需要考虑的因素众多且关系复杂，文中建立的模型尚存在不足之处，比如未考虑末段高低反导装备相互协同时的影响因素，下一步要针对更复杂的情况建立仿真模型。此外，天牛须搜索算法（BAS）作为一种提出时间不长的新算法，相关研究还处在探索阶段，相较于其他成熟的智能算法存在收敛速度比较慢，高维（5 维以上）寻优能力较弱等问题［15］，因此要对算法进行优化改进，满足反导作战高时效性要求，更具实战价值。